左潜“释”《割圆密率捷法》的相关问题探微

王鑫义 郭世荣

(内蒙古师范大学科学技术史研究院，呼和浩特 010022)

左潜(？—1874)，字壬叟，湖南湘阴人。1873年，为徐有壬(1800—1860)的《割圆八线缀术》(以下称“《缀术》”)补草，其中有八式(1)弦求矢、矢求弦、弦求切、切求弦、弧求割、小切求大切、小切求大弦和小割求大矢。为吴嘉善(1818—1885)(2)王海林认为“吴嘉善只是起到了记述作用”(参见参考文献[14]，第42页)似有不妥。述草[1]。丁取忠(1810—1877)认为此项工作“以己意稍变其式，脱误处多所更正，缀小注以便初学”[2]，又将补草后的《缀术》辑入《白芙堂算学丛书》(以下称“《丛书》”)。徐有壬所创的“缀术”使无穷级数的表示与运算趋于简单和规范。左潜通过为《缀术》补草掌握了“缀术”，以“缀术”改造了明安图的《割圆密率捷法》(以下称“《捷法》”)，写成了《缀术释明》(以下称“《释明》”)，该书首次刊行于《丛书》中，是对1839年正式刊行的《捷法》作较全面研究，并加图解简释的第一本著作[3]。事实上，19世纪割圆级数的发展，皆建基于《捷法》。《释明》分上、下两卷，删去了《捷法》卷一“步法”和卷二“用法”，上卷将《捷法》卷三中的“法解上”命为“弧与弦相求图解”，下卷将《捷法》卷四中的“法解下”命为“弧与矢相求图解”。开卷即写明所用版本以及他们各自的工作性质：“明静庵先生原本，左潜释，丁取忠刊。”([4]，页5a)通过对比各版本(3)高红成教授和魏雪刚博士提醒笔者注意各版本的差异问题，并提供了与此文相关的资料，谨致谢忱。的《捷法》和《释明》[5]，左潜在细节上的改造显而易见，之后，崔朝庆在《古今算学丛书》本中，又对《释明》[6]作了校订。

1871—1872年间，左潜、黄宗宪、曾纪鸿聚于长沙。丁取忠与他们共同学习汉译西方数学著作，研究无穷级数、对数等内容，这是“长沙数学学派”最为活跃的一个时期[7]。1873年，丁取忠嘱托左潜为《缀术》补草，左潜将其补为四卷，并认识到了“缀术”能因式立法，因法入算。在《捷法》中，明安图用“第几率”和“又几率”的形式来构造两种公比不同的连比例，但在推导过程中，他又努力将其转化为一组连比例，用一个未知数的形式来处理。事实上，如果欲以借根方处理多于一元的高次方程，需要全面改进其表述系统和运算系统[8]。此后的中算家虽尝试过将借根方发展为多元方程，但没发展起来。左潜发现了“借根方”的局限性，“不能广杜氏之法也，不能立式，究不如天元一之巧变莫测也”([1]，页3a)，并发现了“缀术”的优越性，“试取明氏书驭之以‘缀术’，其递降各率，顷刻可求”([1]，页4a)，这激起了他改造《捷法》的兴趣。《缀术》有式无草，且对钟爱天元术的学者来说，《捷法》既不易理解也未能普及，适于初学者参考的割圆级数著作并不多见，左潜认为有必要进一步详细整理供学者参考的普及读物。

从以下评述中可见左潜诸多工作之一斑：

诸可宝(1845—1903)在《畴人传三编》中指出了左潜的中算背景，并对左潜的工作给予较高评价：“所学自大衍、天元以及借根比例诸新法，无不通贯，且能出己意，变其式，勘其误。”[9]

曾纪鸿(1848—1881)在《释明》序(1875)中提到，左潜以天元入算，并对左潜的工作颇为赞赏：“吾友左君壬叟，曾释徐君青氏《缀术》，又释戴鄂士《求表捷术》，兹又释明静庵‘弧矢捷术’，而一贯以天元寄分之式。于圆率一道，三致意焉，可谓勇矣。”[10]

吴诚在《割圆通解》的序中把左潜的工作与明安图、董祐诚、项名达的工作视为同类：“割圆之法最繁，自杜氏术出，而繁者简。厥后，明氏、陈氏、董氏、项氏、左氏阐其理，徐氏、戴氏、李氏、夏氏、顾氏补其法。”[11]对左潜的工作给予充分肯定。

数学史家钱宝琮(1892—1974)认为：“徐有壬于微积分学传入中国之前自发的创立‘缀术’记法是有积极意义的。左潜于《代微积拾级》(1859)、《代数术》(1872)等书出版以后孜孜不倦地发挥徐氏旧术，似有故步自封之嫌。”[12]

事实上，左潜对“缀术”的认识是比较深入的，对借根方不能很好解决两组连比例问题的洞察力是敏锐的，这并非完全意义上的封闭保守。《捷法》的改造呈现了一个不同要素之间的优劣比较、选择取舍、观念转变的过程，有简化与改进，并非仅为“释”。左潜的改造，推广了“缀术”的应用范围，也可以看到明安图、徐有壬等中算家的著作与思想于左潜的渗透与影响。

1 左潜对《捷法》的改造

以借根方入算的《捷法》为清代中算家无穷级数展开式研究的嚆矢，后来的中算家不同程度受其启发，而《缀术》的完成和补草于西方代数学传入后但未完全取代天元术成为主流方法之时。左潜对《捷法》和《缀术》作“他者”的对照后，发现了借根方、天元术和代数学的一些不同特征，除了术语表达，还有运算问题等。在这样的背景下，他既采用天元术的体例与表达方式，也自觉不自觉地反映一些代数学的内容。

一般而言，在中国古代算学著作中，草起法、术的补充作用[13]，既利于读者对原文进行深入解读，也使文本内容更加清晰化、条理化。由于《缀术》原稿有式无草，左潜以双行夹注等形式作了补草与说明，其中出现的“潜案”和小字注释是左潜补充的内容[14]，还加入了大量的具体算例。这样的补草要求其深入理解徐氏原意，对徐氏“缀术”的运演机制有深刻认识，同时，还要求掌握明氏算理。“潜案”中的化分、通分、方格乘法、尾数截留等多是为《缀术》补草时所创，而明氏在《捷法》中很少涉及。由“潜案”可以说明其解决问题的方法和意图，透视出其方法的多样性。在《释明》中，左潜的见解散在校补或注解中，或以小字注释附于文后，并指明了相关算法的本源，如“即《割圆缀术》中‘还原术’，此即‘借径术’见《割圆缀术》中”([4]，页25b)，还标明了他所校正的舛误。以下从化分、通分、方格乘法、尾数截留等方面分析左潜的改造工作。

1.1 化分

自《捷法》起，化分与通分并不仅仅用于分数，多是对整式而言。《缀术》中的化分方法为：“或以一数乘其母子，或以一数除其母子，变其式不变其实。”([15]，页8b)“潜案”中对此有详解：“凡通分化分皆须变之，以从简也。分母参差则不可以入算，化分者已得各式而分母尚未画(划)一，乃化其分母而后求其分子也。”([15]，页8b)如：

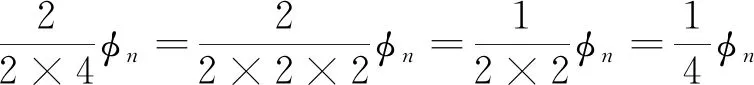
(1)

至于分母用4还是2×2的形式则根据具体的率式而定。

《缀术》中对于加(减)法，首先要保持率名相同，分母不同的两率名相加(减)要先进行处理：“各如其等以相加(减)，有正负者如正负术入之，分母不同者先齐其分。”([15]，页5b)乘法是用一整数乘算式：“常乘其子，若母受除者除母以代之。”([15]，页7b)如：

(2)

若用一整数(不为0)除算式：“常寄于率上，若子受约者约之。”([15]，页7b)如：

(3)

左潜掌握了上述预备知识后，《释明》中再未作详解，而是直接拿来使用。他的化分主要是与各率式中以“级数式”布列有关。“级数”这一术语由李善兰在《代微积拾级》中首创[16]，而徐有壬在《缀术》中称：“各率数即近日新译西算所云‘级数’是也，其求法初若繁重，究之得数级后，其余级数可以推类而得，以等级井然也。”([15]，页21a)说明徐氏已见过《代微积拾级》，对“级数”等术语是清楚的，把“级”解释为“等级”，通过“级数”来把握各项的变化规律。

以《缀术》中的“弦求矢式”为例：

(4)

左潜将上式化为：

(5)

并详解道：“所谓‘级数’者，指将上式化分，九率之十五为三五相乘之数，十一率之一〇五为三五七连乘之数，偶数连乘为分母，奇数连乘为分子。”([15]，页21a)根据左潜所给的简便方法：“所少为乘法则加入其分母，所多为除法则减去其分母。若分母相较，有少无多者则只有乘法，有多无少者则只有除法。”([15]，页9a)在式(4)(5)中，七率原分母与所化之分母相比较少三，故原分母中加入三，以三乘七率原分子得六，再用多余的二除六便得三，故所化之分母中去掉二，后仿此。这一简便方法主要是针对分母的不同之处而言，对其相同之处则保持不变。以“弧背求通弦式”为例，明安图在确定了各率数的分母后，得到下式：

(6)

左潜将上式化为：

(7)

明安图认为各分母渐渐增大后较为不便，把分母分解为有顺序的、较小的数[17]：

(8)

两相比较，一是左潜算至十二率，明安图算至十六率，二是左潜将各率数的分母按“级数式”排列。还可看到，左潜把各率系数化为最简形式，在化分时力求简约快捷。明安图保留形式为便于在算图中统一进行通分，如，二分之四，四分之八等，左潜则化为二的形式，均化为最简形式再运算，包括他所列出的各率式，也都为最简形式，这与明安图的处理方法是有所不同的。

在《释明》中，左潜将偶数连乘为分母，奇数连乘为分子，其化分方法依据齐同术，理论基础是同值变换，达到化繁为简的目的。同时，左潜效仿徐有壬的作法，为使分子分母随乘随消，各率的分母采用其因数的连乘积形式[18]，对于比较简单的运算均不进行演算说明。“齐”和“同”等术语在《捷法》《缀术》和《释明》中多次出现，相应于具体的算法环境，在不同地方出现所表示的运算方法也是不尽相同的。明安图与左潜对各率系数分母的不同表示，主要是“第”“又”的差别，明安图用“第几率”“又几率”引出了公比不同的连比例，为了构造相消，两边同除16(或同乘以十六分之一)，而左潜不用“第”“又”的作法，归为一种连比例，一步到位，因而分母都用4×4×……，而不用16×16×……的记法。

1.2 通分捷法

1874年，左潜在《求一术通解》序中提到：“余增订徐君青先生《割圆缀术》既成，忽悟‘通分捷法’，析分母分子为极小数根而同者去之，凡多项通分顷刻立就。”[19]与化分方法不同的是，通分捷法是左潜在为《缀术》补草之后总结出来的。左潜认识到将一个数分解成素数乘积的重要性，于是用于通分，吴嘉善校阅时曰醇(1807—1880)的《求一术指》时，发现将左潜的这一方法应用于泛母求定母和求乘率，可以极大地简化运算，且能说明原理[7]，这影响并促进了《求一术通解》的完成。

《捷法》中的“齐母通分”说：“将原分母数书于右各率之下，通之，使其同母。”([20]，页917)这里是将左右公比不同的两级数展开式同类项的系数之分母进行通分。明安图在通分时的关键是规定分母和调整分子。

《缀术》“潜案”中的通分方法则是：“分母不同，用通分法互乘齐之。凡通分中有多式者皆用此法为便，多式通分用互乘甚觉繁难且得数必大，既得式后又须多用一化分，此法随乘随除，故较便也。”([15]，页9a)实际上，明安图的通分方法，在规定了分母后，调整分子会变得很容易，而“潜案”中的通分方法，在多式通分时计算量较大，且通分后还需化分。如图1([15]，页6a)，表示率名相同而分母分子不同的通分，即：

(9)

图1

然而，在已知通弦求弧长的问题中，规定分母，调整分子，所得的各率系数中有些是有奇零、不尽的，出现这样的情形用分数来表示。以《捷法》和《释明》中的“通弦求弧背式”为例：

在《捷法》中，求又三率时有5处的得数用带分数表示，求又四率时有13处的得数用带分数表示，任举其中一例：二十四分之一四率自乘，除以一率，得到的二十四乘以二十四分之一七率，统一后的分母为二十四乘以八十，第一个二十四与其它类同不用约简，而第二个二十四需要化简为统一分母中的八十，只需用八十除以二十四就可得到七率的分数，其它各处的方法与此相同。其相当于作了如下处理：

(10)

若取半径为1，通弦记为c，弧背记为2a，则有：

(11)

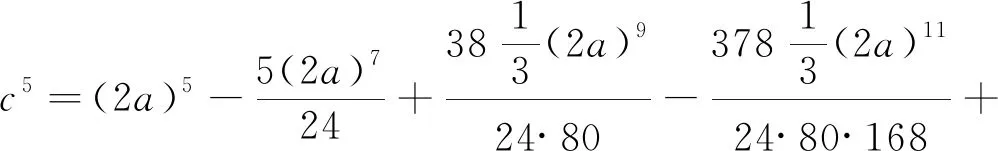
(12)

(13)

……= ……

左潜以求得的弧背求通弦公式为二率，利用“比例法”求得以下各式：

(14)

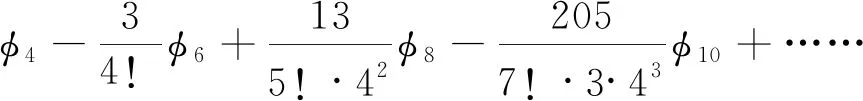
(15)

(16)

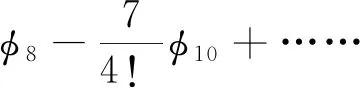
(17)

十率式： φ10+……

(18)

……： ……

不难看出，明安图将计算与调整分子置于同一算图中进行，虽在通分过程中较为省便，但出现了带分数，在计算的过程中，各率数名又不统一，如又三率的表达式中各率数名均为奇数，又四率的表达式中各率数名均为偶数。左潜先用“比例法”径求各率式，得到各率式后，再规定分母，调整分子，相消后即得所求，整个过程中既没出现带分数，也没出现各率数名奇偶不同的情形，且各率数的分母均以“级数式”布列。二者的作法虽只是计算顺序的不同，但为什么会存在较大的差别呢？究其原因有二：一是明安图一开始构造了用“第几率”和“又几率”表达的两组公比不同的连比例，致使在上述过程中出现了各率数名奇偶并存的情形；二是左潜用“级数式”表达各率系数的分母分子，既方便统一，也没有出现带分数，但明安图已指出分母的表达可用连乘的形式，只是当时还没“级数式”的概念。

通分的目的是齐之，《释明》中将各率式乘以中间参数，为的是各率式对应的各率数中各系数与其欲消去的中间参数相齐，依据的仍是齐同术，同值变换仍是其通分的理论根据。《捷法》与《释明》中两种不同的思路代表了两种齐同方式，是对同一问题给出了不同的方法和思路。由此看来，左潜借助于化分与通分，使之成为运算的准则，他的通分捷法是对《捷法》中通分方法的一种简化。

1.3 方格乘法

吴敬在《九章算法比类大全》中将“格子算法”称为“写算”，程大位在《算法统宗》中称其为“铺地锦”，明代多部著作中都有记载[21]。“写算”在后来影响很大，清代数学著作涉及“写算”的很多[22]。《缀术》中的“比例法”，即以比例式列为四行，进行比例相除。其中的乘法较为简单，借鉴“铺地锦”的方法，在《缀术》和《释明》中称为“方格捷法”或“方格乘法”，使人们对“铺地锦”有了新的认识。《丛书》的多部著作中则称为“铺地锦”。

图2

左潜在《缀术》中指明了“方格乘法”的独特之处：“每式中首位率名既定，则以下可以类推，不必逐一求也。若大小八线相求，则中两行相乘须画方格如天元术乘法逐层求之。”([15]，页10a)因为在大小八线相求中，某些率式中的“率数”不是常数，而是多项式，所以要用天元术[23]。左潜又补充：“比例术其二三两行相乘，亦可用方格如天元术乘之，较此更便，但大小八线相求，每层须用方格，则两行相乘自不便再用方格，故草中诸式仍用本法求之，以归画(划)一。”([15]，页12b)实际上，在简单的“比例法”中“乘”和“实”两行(5)即现在所称的“两列”。的计算量较小，操作简单，基本为单项式与多项式相乘，但在大小八线相求问题的“乘”和“实”两行中运算对象变成了多项式，需要进行多项式与多项式相乘，计算量较大，涉及的步骤较多，“方格乘法”不能很好地呈现其运算过程。因此，“方格乘法”可以根据实际的运算对象和计算量的多少来选择。

除此之外，“方格乘法”的重要作用在于：一是在方格内可进行通分的操作，如图1。二是在方格内可进行同类项的连线，如图2([15]，页12b)。“虚线斜联之即如齐等列而相并也”([15]，页13a)，把同一率数的各数用虚线标明，易于同率数相加减。在《缀术》中，徐有壬通过使用“方格乘法”，对“连缀而下”和“斜缀而下”起到了解释作用。《捷法》中的算式都是集中、合并在一个算图中，而《释明》中的“方格乘法”相当于《捷法》中有些连算的分解步骤，还可以拆开分析具体的计算。

1.4 尾数截留

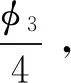
左潜与明安图的做法也是不同的，前者以三率为恒定的乘数，后者算至十五率是因为求至十五率后出现了纯小数或各率系数分子远小于分母[24]，而《释明》中均求至十一率便停止计算。关键在于，左潜在《缀术》中对“级数式”作出了解释，是将各率数的分母化为连乘的形式，认为十一率以后不会影响整体效果，且在《缀术》中就已采用了这样的处理方法。这是左潜吸收西学的结果，不仅把《捷法》中的各率数看作是带有“连续”意义的“级数式”，而且对各率式的简洁性有所要求。而明安图多用自乘的方法，很快便可求得其他各率，求到十一率、十三率时，系数绝对值小于1，求至十五率后截去不用，认为十五率已能满足所需精度，对于弧矢弦相求时，可根据率数的顺序、变化规律直接确定。

1.5 左潜对《捷法》的校勘

通过细致对比发现：左潜在改造表达形式和相关内容时，删繁就简，增补注释，改变术语，校正舛误，使《释明》变得条理清楚，但也有新的舛误产生，包括文字错讹衍脱、语句顺序错乱、图形标记混乱等。经统计，发现一些问题，以资说明(表1)：

表1 删、增、改、校、误的统计说明

其中，左潜所增加的内容多是小字注释部分，以说明解释为主，改动的内容多是术语的表达，校订的内容是在《捷法》原本的基础上作的修改，在校正的60余处中多处被崔朝庆采用，因左潜改动了《捷法》原图中的标记而引起的舛误崔朝庆并未采用。崔朝庆在《古今算学丛书》本的《释明》各卷末既标明了左潜改造的正确之处，也指出了其改造后存在的舛误之处(多为“己、巳”的混用)，并对多处进行了校改，也有左潜校正但崔朝庆未改之处。总体来说，左潜对《捷法》多为无穷级数的表达和文字等形式上的校勘，对明安图在割圆级数中根本性的算法，如弧矢弦之间的互求方法等问题未作改进。这一形式上的改造是值得肯定的，但对一些细节问题处理得较为粗糙。

2 左潜对借根方、天元术和代数学的理解

1873年，左潜在《缀术释戴》序中说：“余因思缀术乃天元一之变法，用以立式，巧变莫测。至求式各法，已详缀术草中，兹不再述。”[25]他指出了天元术与“缀术”的关系，把“缀术”视为天元术的变形，给“缀术”赋予了天元术本有的特性。但他更看到了天元术可以立式立法，“明氏之未能立式也，借根方法取两等数，其分母分子，杂糅繁重而不可通也。其多号少号，辗转互变而不可约也”([1]，页3b)。此外，在《益古演段》的序言中他亦提到：“天元之正负可互易，借根之多少亦可互易，无不同也。凡两边相等数，左边加减至于无数，则右边正负各数即等于左边之〇。”[26]

可见，“缀术”的创造，为左潜审视天元术提供了工具。左潜对天元术与借根方的态度较为明显，是从二者内部出发进行优劣比较，择善而从。“缀术”以天元布式，依术推演，互通变换。虽然天元术与借根方本质都为一元高次方程的列式方法，但不同的运算工具，使两者在表现形式上并不相同[27]。前已述及，明安图利用借根方引入了含有未知数的等式，以“多、少”表示“+、-”，试图设立两个未知数。在左潜看来，明安图未能立式的原因是未改进借根方。在《益古演段》的序言中，左潜则看到了借根方与天元术之间的共性。关键在于，他认识到天元术与借根方的两大区别：一是“多、少”，借根方各项系数为正，且基本上没有负次方项，而天元术的系数正负均可，对于负次方项的表示，简单自在，不需要额外的加号和减号，只需将其与各率数的系数分子结合在一起。二是等式两边的“加减相消”，借根方建立等式后，化简的方式是利用“两边加减”，但必须维持等号两边皆不为零，移项需要改变一次符号，因此借根方不直截了当[28]。例如，在《捷法》中，明安图经过等式两边加减相消后，等式其中一边只有一项。至于天元术，在列出相等的“寄左数”与“又数”后，化简是采取“相消”的方式[29]。其中，“寄分”之法是天元术较之借根方的独特之处。文章《白芙堂诸子对幂级数展开的研究》[30]中，选取了《捷法》和《释明》中的两题进行了比较分析，表明了左潜使用的方法较为简捷，但对其中的原因未作详细说明(6)事实上，左潜在改造前就已认识到借根方与天元术的本质区别，深谙选择天元术作为改造的工具引起计算的简捷是必然的。。

再者，因为天元术可表示整式和分式，而借根方只可表示整式，多项式运算时，天元术可加、减、乘、单项式除，借根方可加、减、乘、除[31]。左潜基于这样的认识，给出了无法立术的缘由：其式为天元式而其数不合天元术，主要表现为整式和分式的异同。事实上，借根方与天元术在术语表达、运算规则上有互补的空间。由此看来，左潜并非是要回归天元术，而是对天元术和借根方的重新审视。

1859年，《代数学》的出版，作为与天元术截然不同的参照系统，引起中算家对天元术的反思和再评估。而左潜对“缀术”有先入之见，认为“缀术”已能解决所遇到的问题，既没有把关注点放在代数学上，也没有试图接受其优越性，又因徐有壬在《缀术》中对代数学的态度，致使左潜对代数学的兴趣不够浓厚。

诸可宝在《畴人传三编》中讲到，左潜对于中西新旧诸法，皆能“循其当然，而抉其所以然”[9]，此评价呼应了左潜所说的：“吾之宗中宗西，不必分其畛域，直以为自得新法也。”[9]左潜理解天元术是为了学习代数而准备，正如丁取忠所言，“为不知代数者，开其先路也”[32]，虽热衷于发扬天元术，但对于西方代数的学习还是抱着肯定的态度。《益古演段》的序中也表明了他的态度：“借根方天元一术异理同……因习代数者必习借根。”[26]而且，左潜在曾纪鸿“借根代数术”之后，“再用借根法以真数求之”同一发商生息问题，也足以显示该法已经不是纯粹的借根方，而同时结合了代数学的符号[33]。

从《丛书》中的著作所涉及的范围来看，在丁取忠的学圈中，是兼容并包天元、借根和代数([27]，页292)，他们将三者并列比较，目的是让读者易于领悟。如，丁取忠在《数学拾遗》中编述割圆捷法的目的是推广、普及[34]。他们已经知道《代微积拾级》等译著，只是兴趣不同，研究内容存在差异而已[35]。研究兴趣是前提，理解本质则是核心。李善兰(1811—1882)和丁取忠在1860—1880年间所主导的学术活动都与自强运动息息相关，也因此都明显地指向西方数学的学习了[36]。事实上，以丁取忠为首的“长沙数学学派”对传入的代数学的回应较为积极，特别是吴嘉善在《代数术》传入之前就受《代数学》影响，对新代数学颇有理解。在《代数术》出版后第二年，他们就在自己的研究中直接或间接地使用了《代数术》中的内容[37]和方法。晚清学者较快掌握了代数学正是因为有天元术、四元术的基础，而左潜等强调天元术的重要性，对理解代数学是有积极意义的。

3 《释明》中由“数”到“式”的改变

明安图在《捷法》中，“详著算式于后，以与图互发焉”([20]，页894)，提供“图解”，作出几何解释，使之“可以形察”[38]。左潜在《释明》中沿用《捷法》原图，几何解释基本与明氏作法相同。《捷法》和《释明》中的“算式”均由三部分构成：连比例各率、各率的分子和各率的分母。不同之处在于：明氏称为“几率数”，左氏称为“几率式”，由“数”到“式”的转变是他改造的独特之处。明氏均给出详细运演程序，并保留具体求解过程，左氏似受了徐氏影响，省去诸多求解过程，“可类推，不列草”的本意即为此。如，明氏算至14率或16率，左氏只算至11率或12率，往后截去不用，等等。

明氏在合并各率数时，将“正、负”置于各率系数分子旁，用“多、少”标记，作加减运算时，用“加、减”以示不同运算。左氏在合并各率数时，都用“加”标记，若率数系数为负，则在所乘系数的分子上用一标记以示区分。即：

明氏：f=ax-by+cz-dv+……

左氏：f=ax+(-b)y+cz+(-d)v+……

左潜对此有注解：“各数命为负者，式之正负相间，欲与式合故也。”([4]，页35a)而这正是借根方表示“多、少”与天元术表示“正、负”的不同特征。

《缀术》中每个“术”相当于一个公式，徐有壬试图从内部探索通则，寻求内在共性。“因式立术”是用“缀术”处理无穷级数展开式问题的重要环节。左潜在《缀术》序言中有过论述：“是故缀术之生，因于明氏而又足以尽明氏之变，明氏之未能立式也。”([1]，页3b)他把“缀术”视为一种可用来立式的方法。《缀术》中的算式实指单项式，各率式实指多项式或无穷级数，“术”为一般的无穷级数。受徐氏“缀术”的影响，左潜在《释明》中以算式表示无穷级数展开式各项，“式”是在“数”的基础上提炼而出。由“算式”转化为“术”的形式，只需列出展开式中的前有限几项，求其以后各项的递推规律[39]。由“数”到“式”的改变，可以估摸出，左潜将“缀术”不仅视为表示方法，还将“缀术”视为推演方法，辅以四种(7)“比例法”“比例商除法”“还原术”和“借径术”。计算方法，以“缀术”运演级数，正如“缀术”的质由“缀术”的形——连缀之形来反映，而“缀术”的形由“缀术”的质来显现。运算和表达在一定程度上是互相补充、可离可合的，这也是为何其改造具有可行性和可操作性的原因。

4 结语

通过分析左潜对一些微观问题的改造，较之于《捷法》中明安图的作法，可以得出以下几点结论：其一，左潜的化分力求简捷，将各率数的分母化为“级数式”。其二，明安图将通分与运算置于同一算图中进行，左潜的通分捷法则是先计算各率式，再进行通分，有效避免了明安图的通分方法所引起的带分数问题。其三，左潜将“方格乘法”移植到了《释明》中，便于分析具体的操作步骤，相当于《捷法》中有些连算的分解步骤。此外，左潜发现天元术能表达公比不同的连比例，选择天元术作为改造的工具，同时，使用天元术也是为了学习代数学而准备。

左潜的改造对《捷法》中繁杂冗长的运算程式无疑是一种简化和改进，并非只是对相关内容的简单缀集。虽在改造中杂有民族情绪，但他还是以借根方、天元术和代数学的优劣、实用与否作为主要参考。不宁唯是，左潜不仅将徐氏“缀术”视为一种级数表示法，而且当作是一种级数推演方法，他对“缀术”的理解是深刻的，以“缀术”寻求与《捷法》内在的共性来实现其改造的目的，这也决定了改造的实施与细节的改进。

致谢衷心感谢匿名审稿专家提出的修改意见。