基于IPSO的桥式起重机吊重防摆系统模糊PID控制研究*

王华荣,谢海智

(1.广东科技学院 机电工程学院,广东 东莞 523083;2.中移铁通有限公司 广东分公司,广东 广州 510088)

0 引 言

近年来,桥式起重机作为货物吊装、转运过程中必不可缺的吊装设备,在机场、港口等场所的应用愈加广泛。但是,由于起重机-钢丝绳-吊重之间存在刚柔耦合特性,吊重在惯性作用下吊运不可避免地会产生摆动。

传统的减摆方法常以降低工作效率为代价,通过降低吊装时的运行速度,并依靠货物重力自然衰减摆动幅度,在消除吊重摆动和定位上花费了大量的时间,增加了工人的操作难度,也存在一定的安全隐患,这就需要寻求一种有效的方法对小车的摆动进行控制[1，2]。

PID控制是最早应用于防摆控制的方法,具有简单、易实现的特点,但由于桥式起重机是一个多变量、参数不确定的系统,PID控制的参数无法实时调整,控制效果受到很大影响。

为提高吊装效率,使桥式起重机精确定位和快速消摆,学者们进行了大量研究,相继提出了模糊控制[3]、神经网络控制[4]、遗传算法等智能控制手段。胡艳丽[5]设计了一种模糊自整定PID防摆控制方法,采用模糊规则对PID的参数进行了调节,取得了较好的控制效果。但是由于模糊规则的制定有一定难度,取决于专家的经验,存在收敛速度慢、准确度不高的问题。针对这一问题,赵华洋等[6]提出了一种基于神经元PID控制策略,利用神经网络自学习功能实现了系统参数的实时调节。但神经网络算法存在计算周期长、运行效率较低的问题。

基于此,本研究根据混沌理论,提出一种基于改进粒子群优化(IPSO)模糊PID控制策略,利用粒子群算法寻址速度快的特点对模糊PID控制器的参数进行优化,提高系统收敛速度和控制精度;同时,对影响吊重摆角的因素进行分析讨论,利用所设计的方法进行仿真和实验,实现吊运小车的精确定位以及摆动幅度的快速抑制,为提高桥式起重机的作业效率提供参考。

1 系统运动特性分析

桥式起重机的吊运系统是一个非常复杂的非线性系统,小车与吊重之间通常采用柔性连接,当起重机的大车或小车在做加速或减速运动时,在惯性作用下,吊重会产生摇摆运动。

吊重的摇摆可以分成两种运动形式:(1)大车和小车同时运动,此时吊重会以悬挂点为中心,以钢绳为半径做球冠面运动[7];(2)大车或小车单独运动,此时吊重在行进平面内做类似单摆的运动。吊重摆动降低了作业效率,并存在一定的安全隐患,因此,需要采用有效的防摆控制方法,控制摆角在规定的范围内;或者当摆角超过规定范围时,摆幅在最短时间内衰减到规定范围内,以利于起重机的快速定位,降低工人劳动强度。

为便于分析,根据起重机实际工作情况,笔者作以下假设:

(1)大车和小车在各自运动方向上自然解耦,对吊重摆动影响效果相同,加之起重机在进行吊装作业时,大车通常处于静止状态,因此,为简化分析,在建立力学模型时,不考虑小车机构的运动;

(2)不计钢丝绳的质量,并忽略钢丝绳的弹性变形以及空气阻力的影响。

根据小车运动时的受力情况,笔者建立系统的简化力学模型,如图1所示。

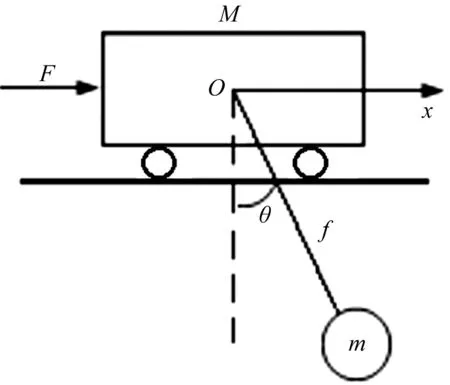
图1 桥式起重机的简化模型

当小车运行距离为x时,在广义坐标系统(θ,l)中,小车的拉格朗日动力学微分方程为[8]:

(1)

(2)

(3)

式中:M—小车质量;m—吊重质量;θ—吊重摆角;l—钢丝绳长度;μ—小车与轨道间摩擦系数;x—小车移动距离;F—小车受到的驱动力;f—钢丝绳的提升力。

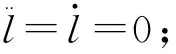
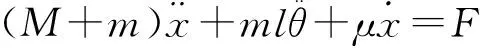
(4)

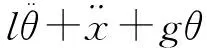
(5)

由上式可见,当吊重质量一定时,钢丝绳的长度和小车的加(减)速度是影响吊重摆角的关键因素。因此,这就需要设计一种有效的小车位置控制策略,对小车的位置及运动状态进行实时的控制。

2 控制策略

2.1 改进PSO算法

基于鸟群行为通过迭代过程寻求最优解的优化算法称为粒子群算法。将粒子看作是一个解向量,通过个体之间的协作以跟踪粒子的速度和位置,寻求最优解,广泛应用于对连续域的优化问题[9]。

假设在一个N维空间中,由m个粒子构成一个群落,设Xi和Vi代表粒子i的空间位置和速度,d为变量的维数,且i=1,2,…,m,d=1,2,…,N;利用目标函数计算适应值,再由适应度函数决定粒子的优劣,通过迭代不断更新粒子的位置和速度,可实现全局寻优。

t时刻粒子的更新策略可表示为[10]:

(6)

(7)

(8)

传统的粒子群算法容易陷入局部最优,出现早熟现象,使寻址精度受到影响。因此,为增加粒子认知能力及搜索范围,笔者对PSO算法进行改进,提出一种新的惯性权重调整方法,即:

(9)

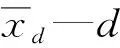
对PSO算法改进后,粒子在寻址过程中,ω先变大,随后又变小,这样不仅扩大了搜索范围,还能够大大提高搜索的精度,从而可以克服粒子群算法的早熟问题。

2.2 基于IPSO的模糊PID控制

由于PID参数不能自动调节,无法适应非线性时变系统。为了获得更好的控制效果,通过把模糊推理运用于PID参数的整定,来补偿同步系统因非线性和时变性所导致的同步误差,该方法的应用比较广泛。但是,模糊规则的制定过程较为复杂,准确性取决于规则制定者的经验[11，12]。

因此,本文采用IPSO方法对隶属度函数进行优化,可以大幅提高系统收敛速度,解决PSO算法效率低的问题,从而实现PID参数的动态调整。

其具体步骤如下:

(1)确定适应函数,并初始化参数。确定粒子的位置、速度、学习因子以及迭代次数等参数;

(2)计算粒子的适应度数值。对训练样本进行学习,得到各粒子的训练误差,记为各粒子的适应度值,并与该粒子的最优适应度值进行对比判断并更新;

(3)采用式(8)计算惯性权重,并通过式(9)进行权重改进,然后利用式(6,7)更新粒子的速度和位置;

(4)将粒子的位置和速度依次赋值给模糊控制器,优化隶属度函数,运行控制系统模型,并输出性能指标;

(5)判断是否满足终止条件,如果满足则求出最优解,否则转至步骤(2)。

IPSO优化PID参数的流程如图2所示。

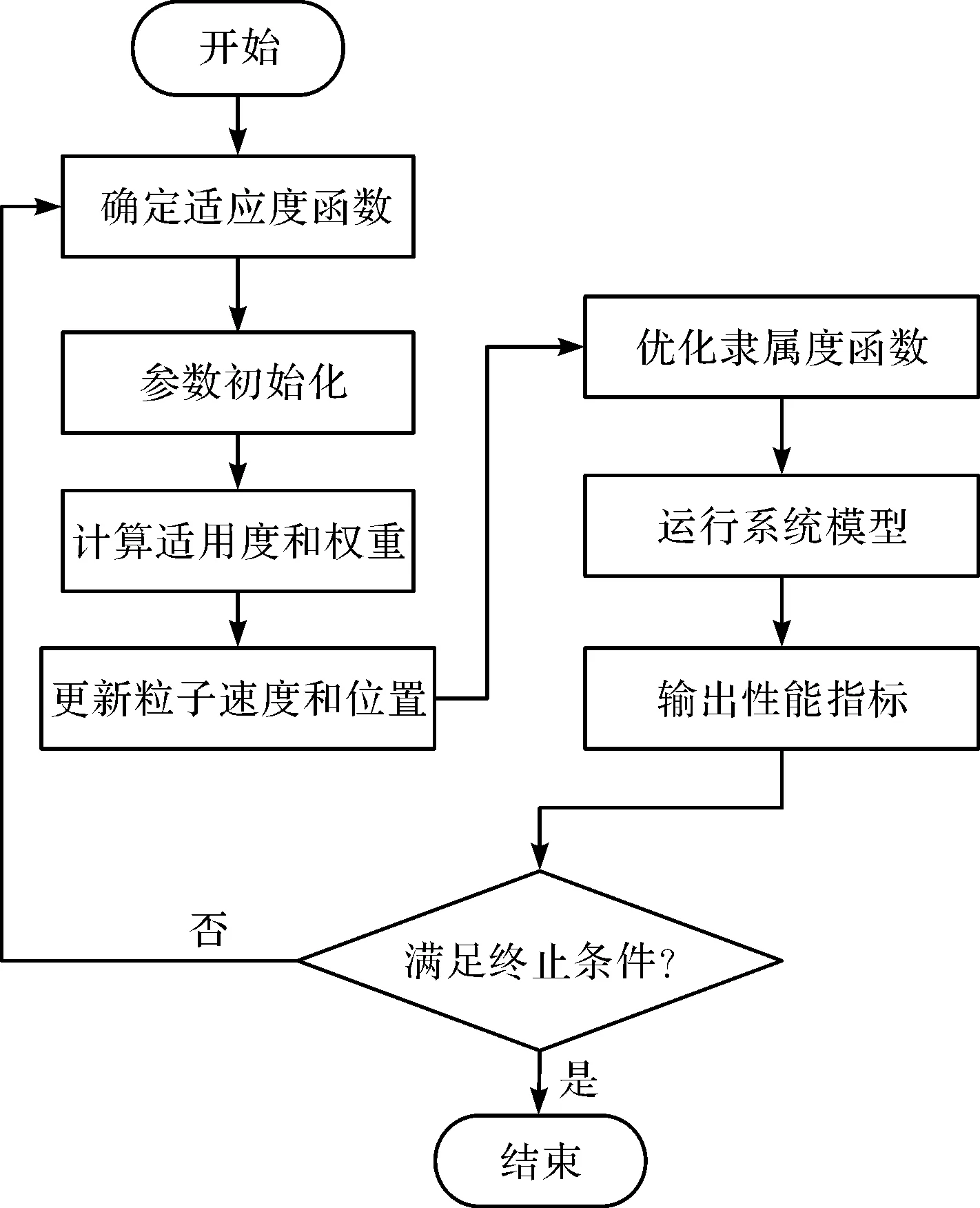
图2 IPSO优化模糊PID参数的流程

笔者将吊重的摆角和小车位移作为系统输入,误差结果作为输出,来设计模糊控制器;采用IPSO优化PID参数,通过目标函数计算粒子适应度值,调整模糊论域的取值范围,实现系统参数的优化;通过不断调整PID控制参数,用以降低目标函数的输出值,从而达到提高系统精度的目的。

控制器结构如图3所示。

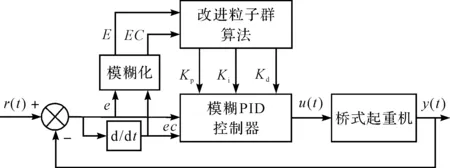
图3 基于IPSO的模糊PID控制器结构

3 仿真分析

笔者将改进粒子群优化的模糊PID控制策略应用于桥式起重机控制系统中,采用MATLAB软件编写算法程序,并在Simulink模块环境中进行仿真分析。

为避免适应值评估和计算时间过长,提高粒子的寻优精度和寻址速度,此处函数设置为10维,迭代次数为200次,粒子数量为20,学习因子c1=0.8,c2=1.2;同时,为使算法前期拥有较强的全局搜索能力和后期拥有较强的局部搜索能力,使其保持整体平衡,此处分别取最大和最小权重为ωmax=0.9,ωmin=0.4。

此处以单位阶跃信号作为系统输入,仿真时间为10 s。在实际工作中,受环境影响较大,为检验系统的抗干扰能力,在仿真的第5 s时,加入一个干扰信号,并与其他控制方法进行对比。

单位阶跃信号仿真结果如图4所示。

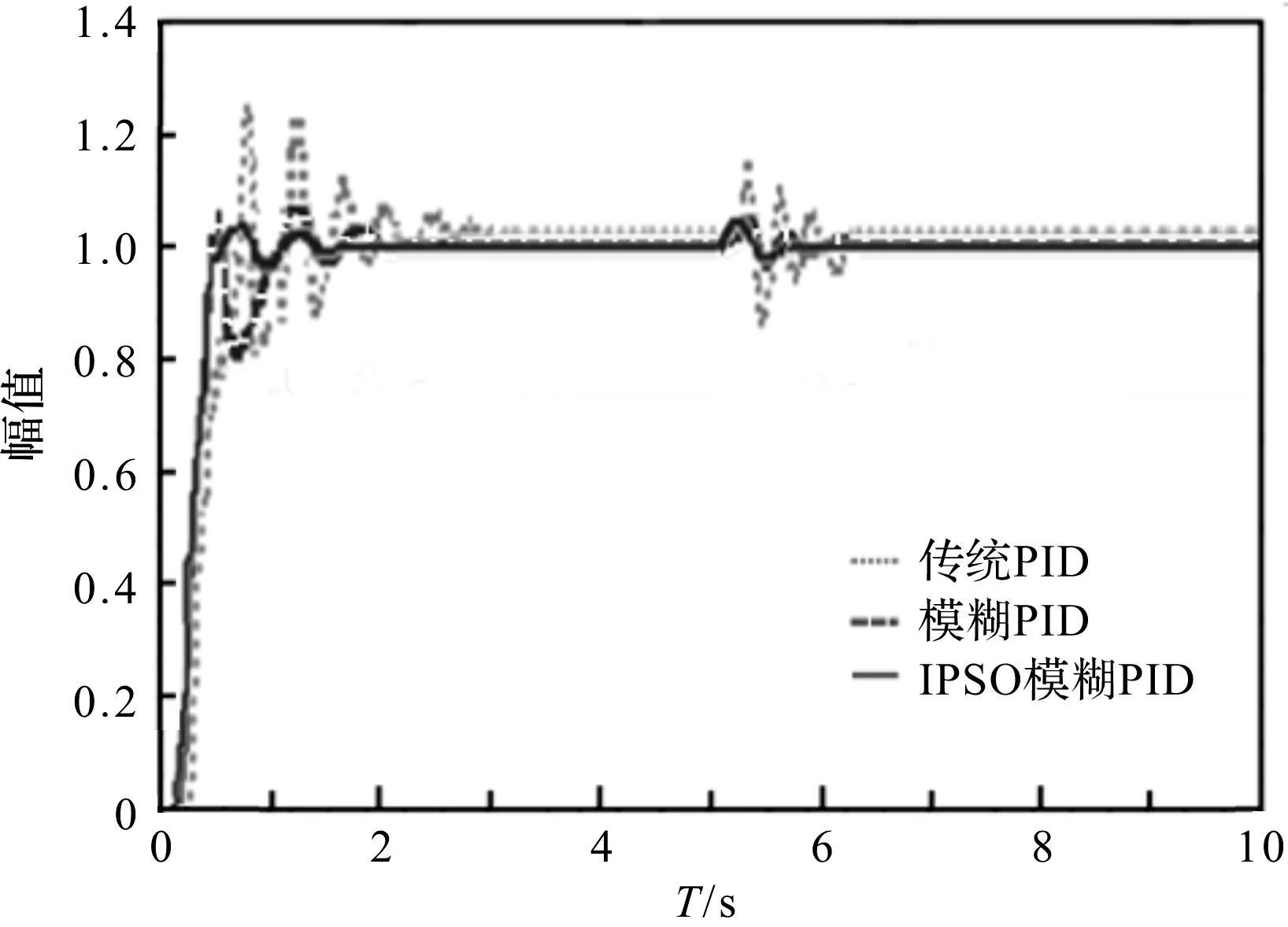
图4 单位阶跃信号仿真结果

由图4可见:IPSO优化模糊PID控制的超调量小,响度速度快,达到稳态状态时间短,控制效果好,抗干扰能力强。

为进一步分析控制策略的有效性,笔者将采用3种控制方法得到仿真结果进行对比,如表1所示。

表1 仿真结果对比

由表1可以看出:与传统PID控制相比,ISPO优化模糊PID控制策略超调量缩减了20%,稳态时间缩短了40.4%,误差减少了11.4%。该结果说明,笔者所提出的控制方法得到的控制精度最高,可以满足桥式起重机吊减摆要求。

4 吊重摆动影响因素分析

由式(4,5)可知,当起吊的重量一定时,钢丝绳的长度和小车的加速度是影响减摆系统的主要指标。

为分析各因素对吊重摆动的影响,笔者首先保持起吊重量为m=500 kg,位移x=2 m,小车加速度为a=0.15 m/s2不变,分别采用钢丝绳长度l=2 m,l=2.5 m,l=3 m进行仿真;然后,保持起吊重量为m=500 kg,位移x=2 m,钢丝绳长度为l=2.5 m不变;分别取小车的加速度为a=0.2 m/s2,a=0.3 m/s2,a=0.4 m/s2进行仿真。

钢丝绳长度对摆动的影响的仿真结果如图5所示。

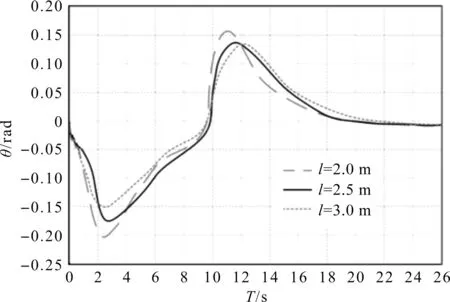
图5 钢丝绳长度对摆动的影响

由图5可以看出:在起升重量不变的情况下,不同长度的钢丝绳对吊重摆角影响不大,摆角衰减时间几乎不受影响,这说明不能把改变绳长作为减摆的主要措施。

小车加(减)速度对摆动的影响的仿真结果如图6所示。

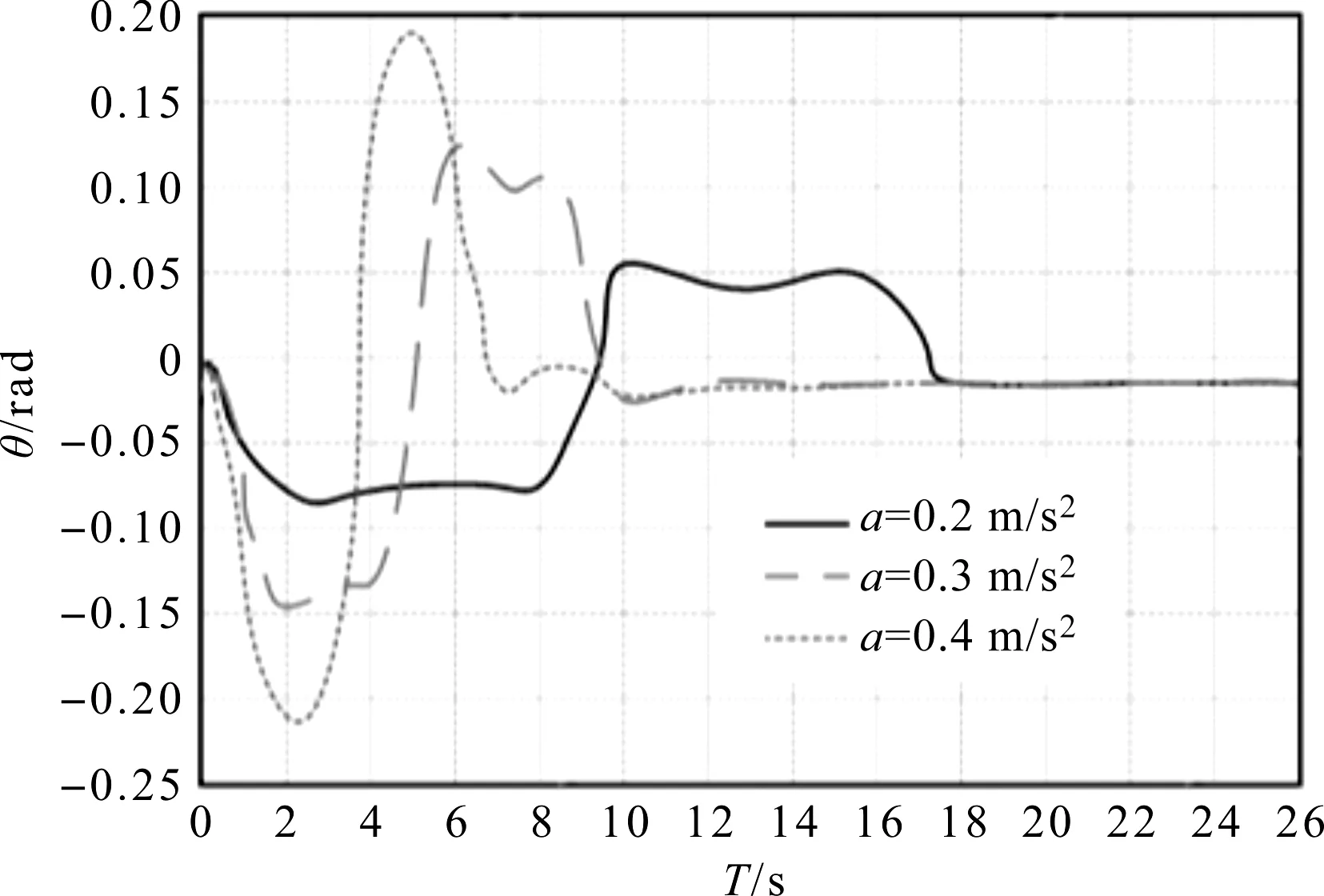
图6 小车加(减)速度对摆动的影响

由图6可以看出:在起升重量不变的情况下,小车的加(减)速度对吊重摆角影响较大,摆动幅度随小车加(减)速度的增大而增大。

该结果说明,可以通过改变小车的运行状态来抑制吊重摆动,但小车的运行速度又影响了工作效率,所以在实际工作中,应该基于防摆系统合理控制小车的运行状态。

5 实验测试与结果分析

为验证所用控制策略的有效性,笔者基于某型桥式起重机进行实验测试。

该起重机的各项参数如下:

跨度为20 m,小车驱动电机功率6.3 kW,电机转速1 000 r/min,制动力矩200 N·m。

在实验过程中,起吊重量为500 kg,小车以0.25 m/s2的加速度运行距离为1.2 m时开始制动,采用不同的控制策略进行防摆控制,然后对小车的位置和吊重摆角进行数据采集,时间为50 s。

不同控制方式位移变化的测试结果如图7所示。

图7 不同控制方式位移变化

不同控制方式摆角变化的测试结果如图8所示。

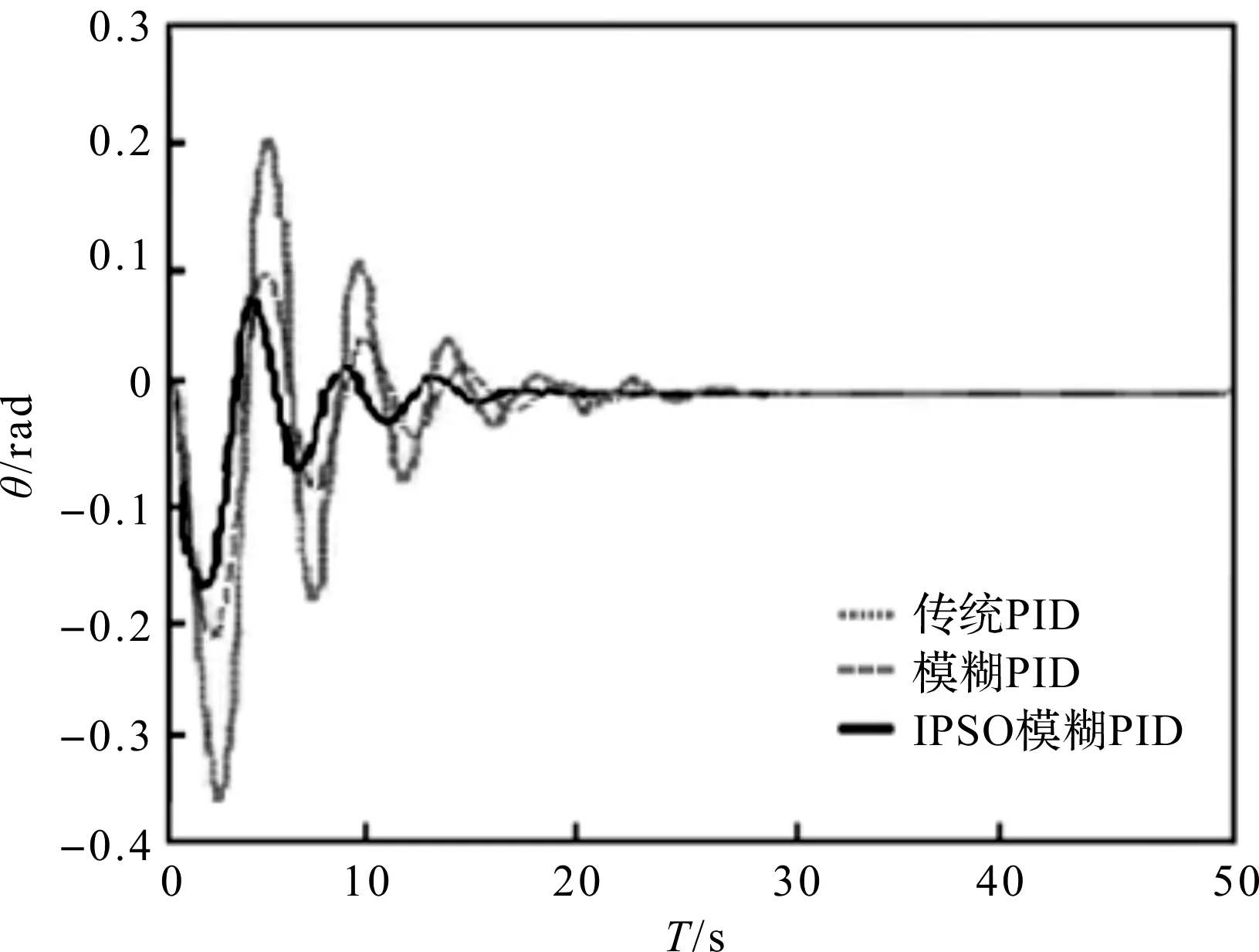
图8 不同控制方式摆角变化

为进一步说明所用方法的有效性,笔者将采用3种控制方法得到的实验结果进行对比,如表2所示。

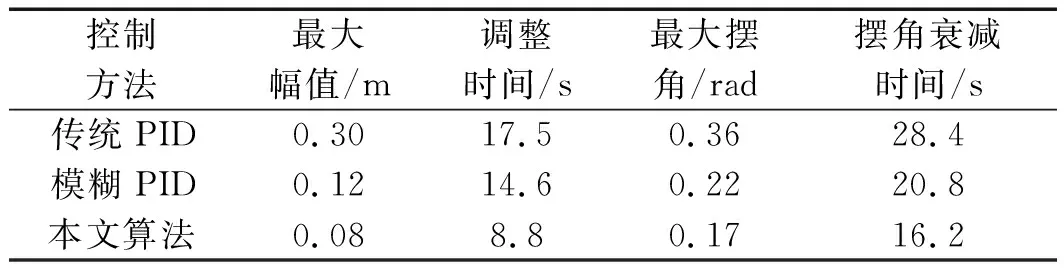
表2 实验结果对比

由表2可以看出:IPSO优化模糊PID方法能使小车准确定位,并有效消除吊重的摆动;相比传统PID控制策略,小车的定位精度提高了73.3%,定位时间缩短了49.7%,消除摆角的时间缩短了43%,控制效果更为有效。

6 结束语

为解决桥式起重机吊工作过程中吊重定位精度差、吊重摇摆以及工作效率低的问题,笔者在保证作业安全性和运行稳定性的基础上,提出了一种基于改进粒子群优化的模糊PID控制策略,具体过程和结果如下:

(1)利用Lagrange动力学微分方程分析影响吊重稳定性的因素,确定了控制参数指标;

(2)对粒子群算法的更新策略进行改进,并通过改进算法优化模糊PID控制器的参数,使其更具适应性。同时,以运动小车的位置和吊重的摆角作为研究对象,进行了仿真分析和实验测试,并分析了钢丝绳的长度及小车加(减)速度对减摆效果的影响;

(3)当吊重的质量一定时,通过仿真分析发现:钢丝绳的长度变化对吊重摆角的影响并不明显,而小车的加(减)速度对摆角影响较大,摆动幅度随加(减)速度的增加而变大。

由此可以得到结论:基于IPSO优化的模糊PID控制策略可有效地实现小车精确定位和快速消除吊重摇摆,克服了吊重扰动对小车位置的影响;该控制策略的抗干扰能力强、控制效果好。

与传统PID控制方法相比,采用该控制策略后小车的定位精度提高了73.3%,消除摆角时间缩短了43%,大大提高了起重机的作业效率和安全性。