基于改进型ADRC的四旋翼无人机运动控制

段淑霞，王力超，周群利

(1.芜湖职业技术学院，安徽 芜湖 241000；2.安徽工程大学，安徽 芜湖 241000)

随着科技的发展，因四旋翼无人机在无人探测，军事应用，灾害监测等方面有着广泛的应用[1-3]，且其具有方便携带、结构简单、探索方便及垂直升降的特点，因此四旋翼无人机受到了越来越多国家的关注。然而在其实际应用过程中，四旋翼无人机易受到外界环境及自身系统的欠驱动性和耦合性的干扰，吸引了广大的学者对其不足之处进行了研究[4-6]。

因四旋翼无人机精确的数学模型难以建立，Mallavalli采用传统的PID控制器控制其姿态[7]，但实际运用中抗干扰效果略有欠缺；博康针对Mallavalli所研究的问题[8]，对PID控制器进行了改进，设计了自适应PID控制器，结果显示在无干扰情况下具有良好的姿态控制效果，但遇到机翼及外界不确定的风的影响时，会受到比较大的扰动；杨桑和Yildiz采用自适应控制方法以此来降低控制系统对四旋翼模型依赖的问题[9-10]，然而从仿真结果显示虽然模型问题得到了解决，但仍存在一些控制精度及鲁棒性不强的问题。为了应对控制系统鲁棒性不强的问题，Muliadi采用神经网络与PD控制相结合的方式来解决稳定性及不确定扰动的问题[11]；郭昇针对四旋翼无人机中欠驱动问题[12]，将无人机系统分为两个系统，一个全驱动系统，一个欠驱动系统，然后分别用基于PID的滑膜控制器相结合进行处理，从而解决了欠驱动问题。针对四旋翼无人机出现的饱和等问题，部分学者将自抗扰控制器运动到无人机当中，取得了良好的控制效果。如对无人机欠驱动问题，洛图福做了进一步的改进[13]，其采用基于有限时间元的自抗扰控制对四旋翼无人机进行控制，以此提高控制系统的控制能力；李乐宝将如何抑制干扰和提高控制精度的问题作为研究对象[14]，设计了滑膜变结构对四旋翼无人机的未知进行控制，并采用扩张状态观测器用来提高四旋翼无人机运动时的跟踪精度问题；邱潇颀针对四旋翼无人机的输入饱和问题提出了自适应的自抗扰控制策略[15]，成功解决了四旋翼控制器在饱和情况下和外界干扰下的问题，有效地提高了四旋翼无人机的控制效果及容错能力。

自抗扰控制是韩京清先生于1998年提出的一种控制方法，该控制方法在PID基于上进行改进，设计了自抗扰控制器，其由跟踪微分器，扩张状态观测器和非线性状态误差反馈控制率三部分组成，并且保留了基于误差消除误差的控制思想，其使用大量的非线性函数使得控制器具有较强的鲁棒性、较快的响应速度及能保持很高的精度，解决了一般控制器不好解决的一些问题。本文采用改进型自抗扰控制器对四旋翼无人机运动系统进行优化，针对自抗扰控制器中非线性函数存在部分区间不可导和可能会引起无人机系统在实际运行过程中出现的抖动问题，设计了新型非线性函数，并由新型非线性函数对扩张状态观测器和非线性状态误差反馈控制率进行了改进，最后利用改进后的自抗扰控制对无人机系统进行仿真，结果显示所设计控制器的优越性能。

1 无人机运动模型

图1为无人机运动示意图。

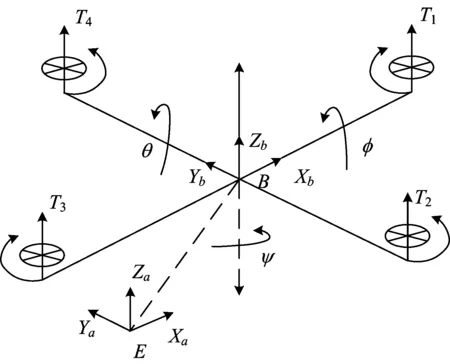
图1 四旋翼无人机运动示意图

为了描述四旋翼无人机的模型，首先要对四旋翼的动坐标系E-xa,ya,za和定坐标系o-xb,yb,zb进行建立，并且定坐标系到动坐标系的转换关系如式(1)所示。

(1)

在建立四旋翼无人机运动模型之前，先对无人机系统做两点假设：1)无人机为刚体，外界的变化不会影响四旋翼无人机的结构；2)无人机的重力加速及其变化和空气阻力等外界变化不会对无人机系统造成影响。在此假设下运用牛顿-欧拉法建立无人机系统运动模型，如式(2)所示。

(2)

其中，各自由度之间的控制量和转速之间的关系如式(3)所示。

(3)

式中各物理量表示的意义如表1所示。

表1 各物理量及意义

2 自抗扰控制器

2.1 自抗扰控制器及其组成

自抗扰控制器由三部分组成：1)跟踪微分器：对输入信号进行优化处理，以提高高质量的控制量；2)扩张状态观测器：针对系统内部一系列的扰动及不确定模型进行观测，从而提高控制系统的控制能力；3)非线性状态误差反馈控制率：将跟踪微分器与扩张状态观测器的输入量进行非线性组合，从而为系统提供更优的控制效果。如图2所示。

图2 自抗扰控制组成图

2.2 改进型非线性函数

非线性函数是自抗扰控制的核心函数，非线性函数的选取与设计是优良控制的重要保证。其选取与设计应遵循以下原则：1)在原点处可导且光滑；2)收敛性较好；3)原点处值恒为0。

传统的非线性函数fal(e,α,δ)如式(4)。

(4)

在分段点处求导得：

从上式可以看出，虽然传统的非线性函数是连续的，但存在不可导点，因此需要对之改进优化。具体设计如下：

当|e|>δ时，新函数nfal(e,α,δ)的表达式不变。当|e|≤δ时，nfal(e,α,δ)函数如式(7)所示。

nfal(e,α,δ)=l1sine+l2e2+l3tane

(7)

因sin(·)函数收敛性更强，运用差值拟合得到：

(8)

求解得到：

(9)

最终得到：

(10)

为了验证新型非线性函数的性能，对传统非线性函数和新型非线性函数进行仿真如图3所示。

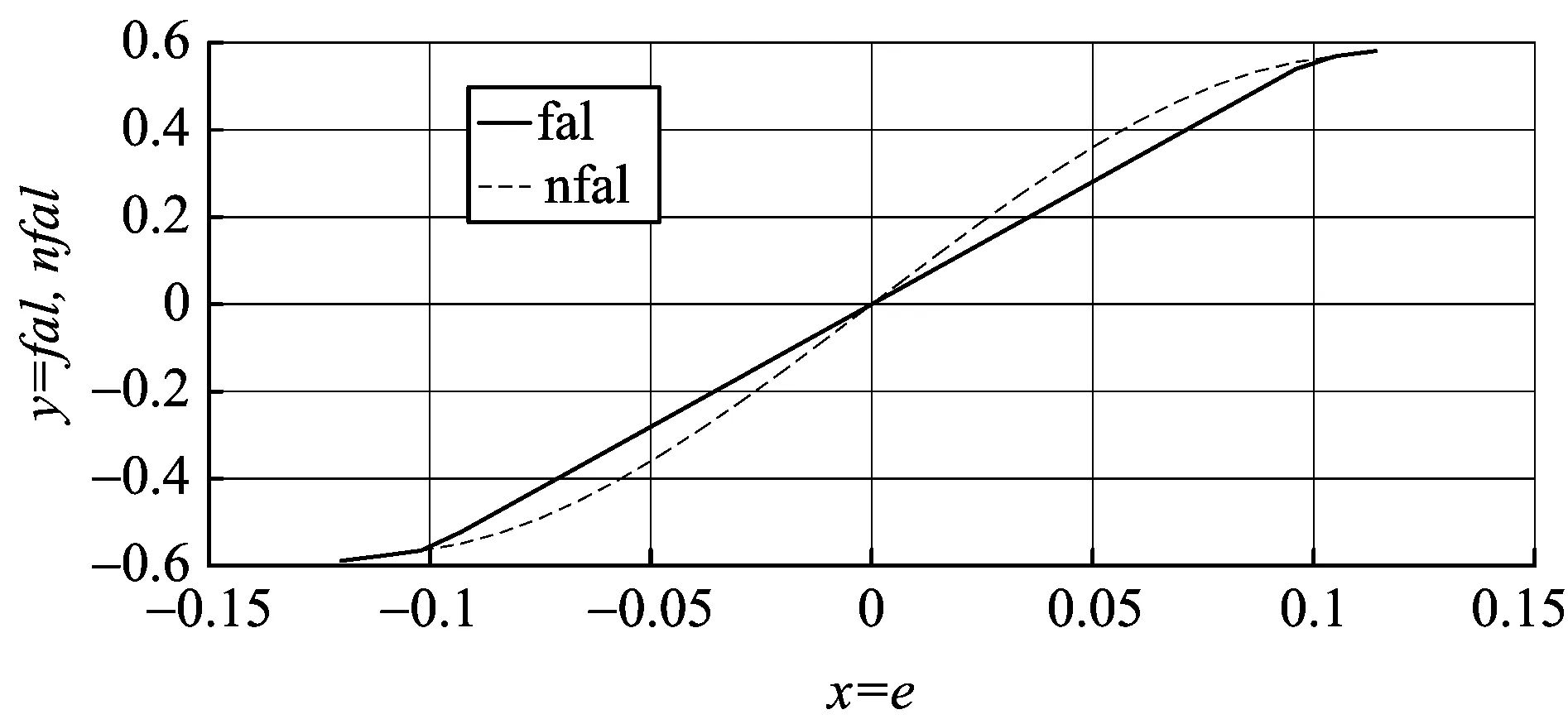
图3 nfal(e,α,δ)函数与fal(e,α,δ)函数的比较

从图3中看出，新型非线性函数比传统的非线性函数更加光滑，且可导性更好。本文中的扩张状态观测器与非线性误差反馈控制率就是基于此函数设计的。

3 改进型自抗扰控制器

3.1 跟踪微分器

跟踪微分器主要作用是提高输入信号的质量，其将输入信号进行分解，从而获得更优的控制量，并将优质的控制量作用于扩张状态观测器，从而提高系统的控制能力。跟踪微分器的算式为(11)所示。

(11)

其中，x(t)为四旋翼无人机的输入信号，u=fan(x1-Xr,x2,r,h0)的具体算式如下：

其中，h为步长，r为跟踪系数，Xr为四旋翼无人机的输入，x1为跟踪四旋翼无人机的信号。

3.2 新型扩张状态观测器

扩张状态观测器是控制器的核心，其主要作用主要有两点：1)四旋翼无人机的输出信号反馈于新型扩张状态观测器，经新型扩张状态观测器的处理，信号分别作用于跟踪微分器和补偿装置；2)对各种因素引起的扰动进行补偿，包括但不限于不精确模型的输入，四旋翼无人机系统内外的扰动。通过新型扩张状态观测器的处理，使得系统的处理不确定的能力得到有效的提升，从而提高控制器整体的控制性能。新型扩张状态观测器具体算式如下：

(15)

其中，新型非线性函数已在上节给出，ε1为四旋翼无人机的反馈误差，u为四旋翼无人机的控制量，b0为补偿系数，β11,β12,β13为增益，α1,α2,α3为非线性系数。

3.3 新型非线性状态误差反馈控制率

新型非线性状态误差反馈控制率主要作用是提高控制器的稳定性和抗扰动能力，其将跟踪微分器和新型扩张状态观测器所输出的量进行非线性组合，从而提高了控制器的工作精度。新型非线性状态误差反馈控制率具体算式为：

(16)

其中，e1,e2为误差和误差的微分，α是非线性系数，β21,β22,β23为增益，δ为滤波因子。

3.4 自抗扰控制器

以上对新型非线性函数进行了设计，并且在新型非线性函数的基础上对自抗扰控制器的扩张状态观测器和非线性误差反馈控制率进行了改进，从而设计了新型自抗扰控制器。为了验证改进后的效果，将对所改进的控制器进行仿真，其具体参数如表2所示。

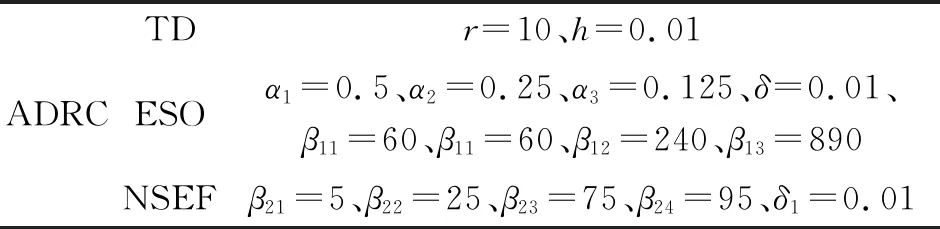
表2 自抗扰控制参数

分别用自抗扰控制，改进的自抗扰控制和PID三种控制器进行验证，从图4可以看出，虽然三种控制器最终都到达了稳定状态，但PID控制器的超调和到达稳定时间最长，而传统的自抗扰控制器控制性能位于改进型和PID控制器之间，改进型的自抗扰控制器响应时间最短，超调最小，拥有更好的控制性能。

图4 阶跃响应

图5为阶跃响应时三种控制系统受到同样大的扰动时的响应曲线，从图5可以得到，当受到同样的扰动时，PID控制器受到的影响较大，其恢复所需要的时间更长，且恢复过程中稳定性会受到一点影响，传统ADRC受到同样的扰动时具有较快的恢复性且受扰动影响最小，改进型ADRC在受到同样的定常扰动时，其恢复时间和抗干扰能力最强，具有很强的稳定性能。

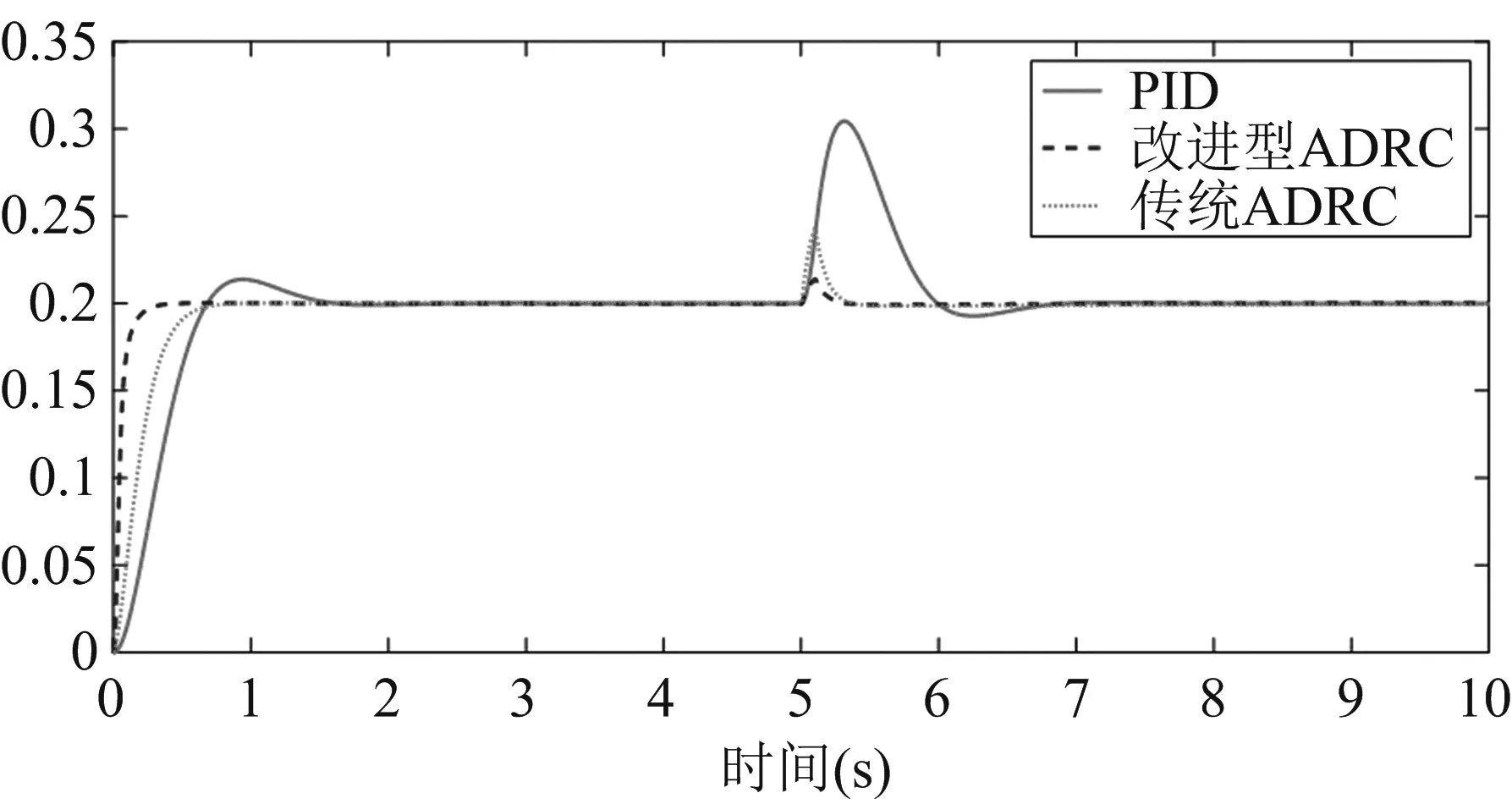
图5 定常扰动

图6为三种控制器遇到高频扰动时的响应，从结果可得，当在方波状态下遇到高频扰动，PID的控制器的波动大，且幅值较高，而传统ADRC和改进ADRC波动较小，其中改进ADRC的鲁棒性最强，稳定性最高，即使在高频大幅值的扰动下也几乎无波动，其抗干扰能力最优。

图6 高频扰动

4 实验验证

从上一小节可以看出改进型自抗扰控制器优越的控制性能，为了进一步说明改进型自抗扰控制器运用于四旋翼无人机上的控制能力，对其进行实验验证。

对同样的参数的自抗扰控制器与改进自抗扰控制器以及PID控制在所搭建的四旋翼无人机平台中验证。其中，四旋翼无人机的具体参数如表3所示。

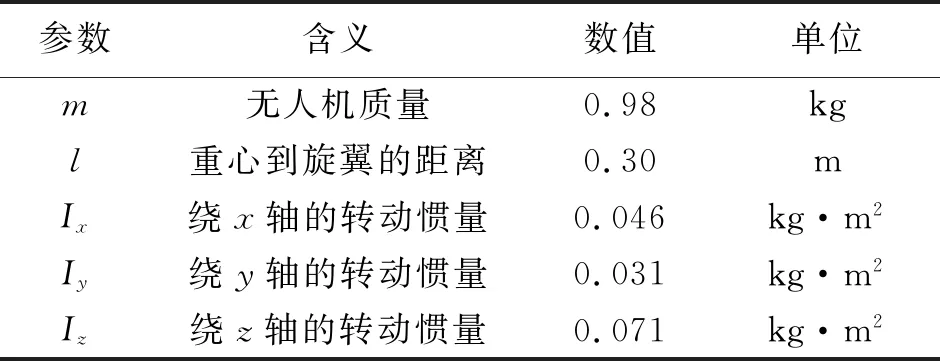
表3 四旋翼无人机参数

图7(a)为四旋翼无人机的滚转角响应，图7(b)为四旋翼无人机的俯仰角响应，图7(c)为四旋翼无人机的偏转角实验图，图8为对四旋翼无人机高度的实验图。

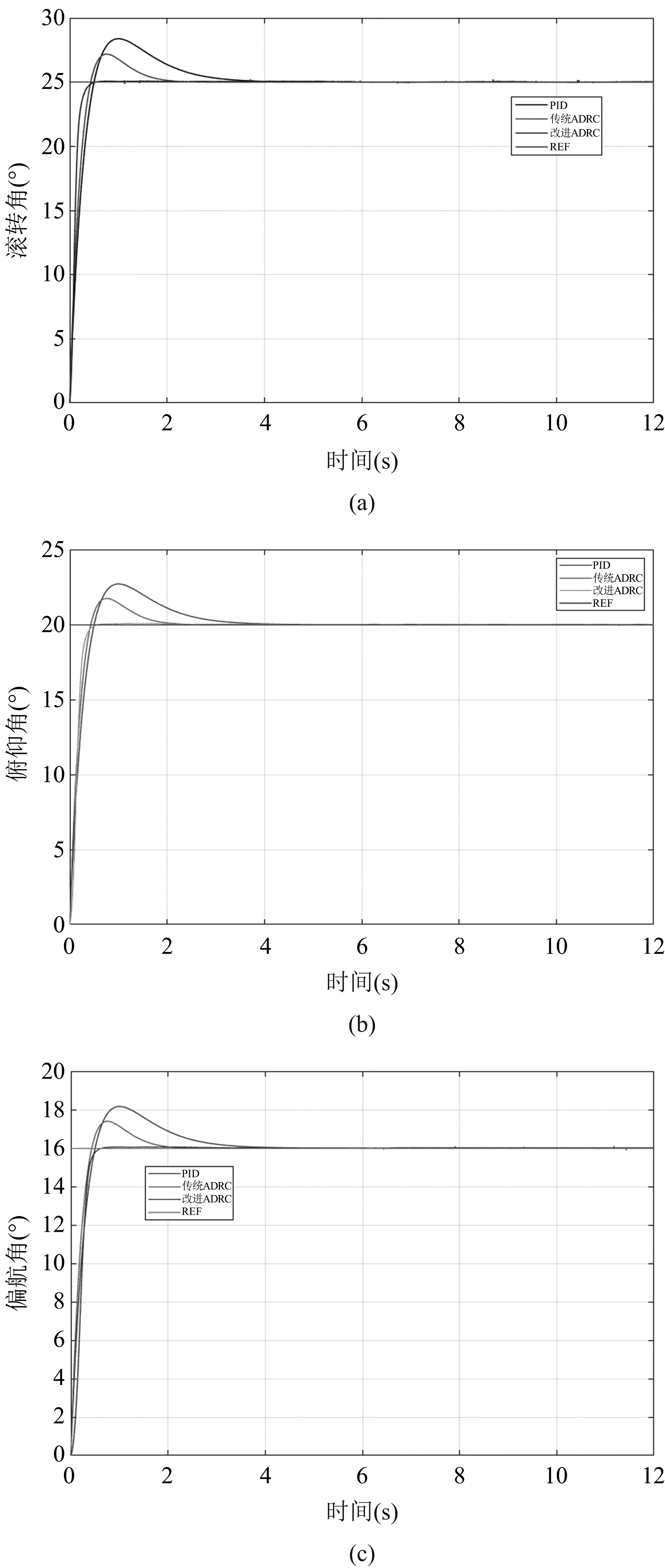
图7 四旋翼无人机三个姿态响应

图8 四旋翼无人机高度响应

在图7四旋翼无人机的三个姿态角控制中，PID控制器的到达指定旋转角度时间最长，且初始时有较大的超调，而传统ADRC在四旋翼无人机的姿态角控制时其控制性能位于PID控制与改进ADRC控制之间，改进ADRC控制器在四旋翼无人机的姿态角控制时表现出优异的控制性能，在图8可以看出，在四旋翼无人机高度的响应曲线中，三种控制器最终都能到达稳定运行高度，改进型ADRC能准确快速地到达指定的高度位置，几乎高度无超调，而PID控制器和传统ADRC控制器在四旋翼无人机高度的响应中，会有一定的高度超调且到达稳定高度运行的时间较长，所以，PID控制器的控制效果无论是在四旋翼无人机的姿态还是高度控制方面，其快速性和稳定性均较弱，传统ADRC控制器的控制效果运用于四旋翼无人机中较PID控制较好，但仍然存在一定的超调和到达稳定时间长的问题，改进ADRC在四旋翼无人机中的控制效果较优，快速性和到达稳定时间较为理想，拥有更好的控制性能。

图9(a)为四旋翼无人机受到定常扰动时的滚转角实验曲线，图9(b)为四旋翼无人机受到定常扰动时的俯仰角实验曲线，图9(c)为四旋翼无人机受到定常扰动时的偏航角响应，图10为四旋翼无人机受到定常扰动时的高度响应曲线。基于图7和图8的实验，当无人机在正常运行过程中受到外界的定常扰动时，响应曲线如图9和图10所示。

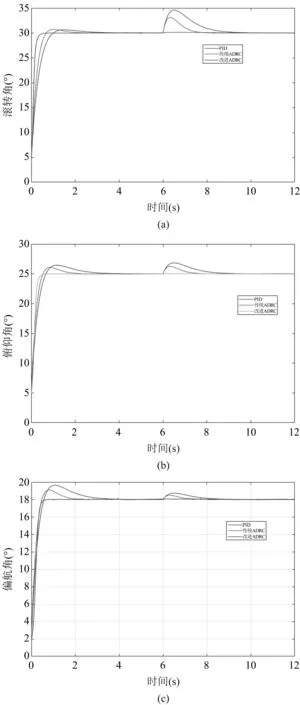
图9 定常扰动三个姿态角响应

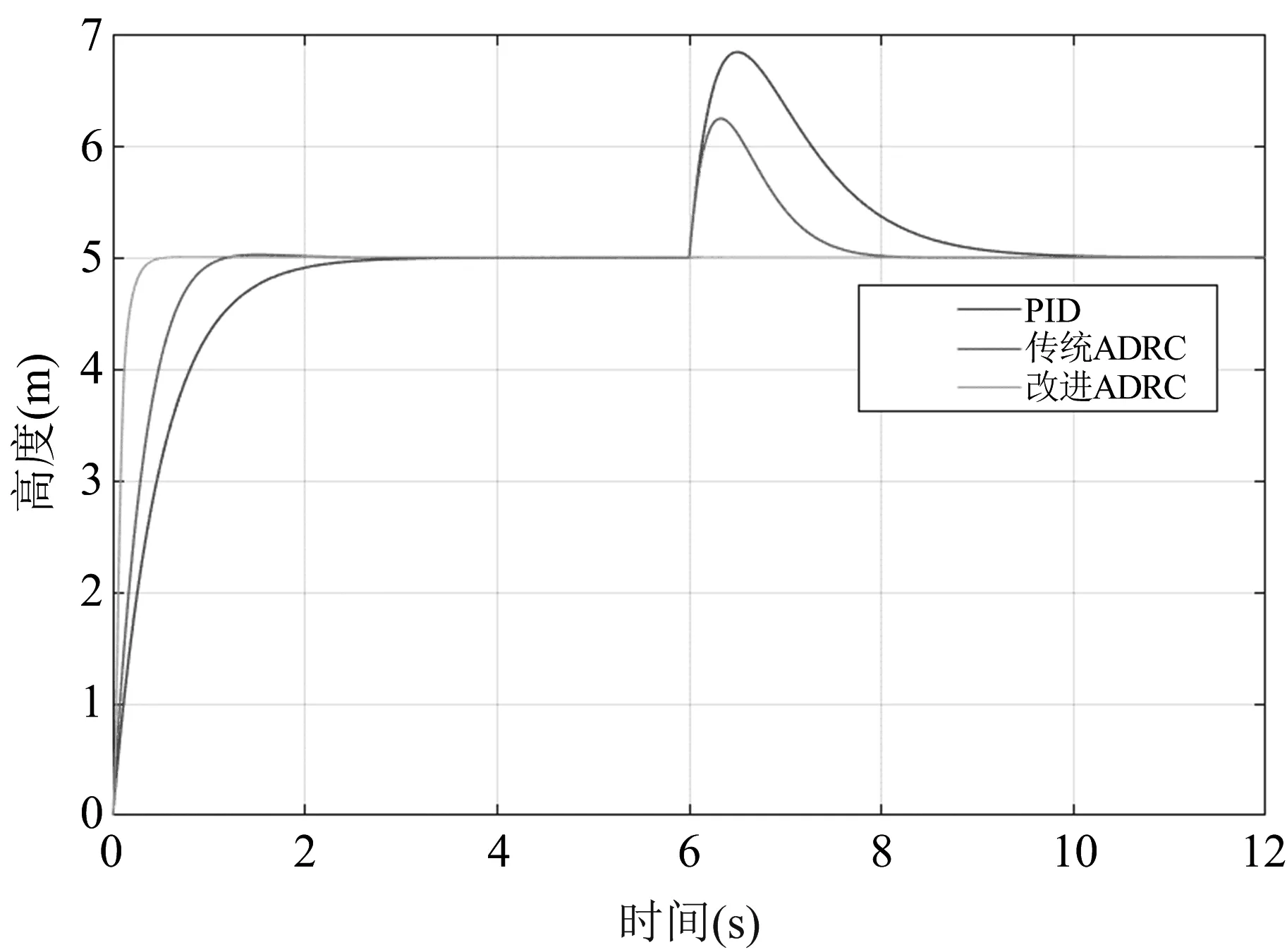
图10 定常干扰时高度响应

在图9四旋翼无人机的三个姿态角受到定常扰动时的控制中，PID控制器由初始受到扰动到恢复稳定的旋转角度所需时间最长，且在三个姿态控制角中受到定常扰动时的表现性能不理想，受到外界干扰时偏离原定的姿态角度较大，而传统ADRC在四旋翼无人机的姿态角突然受外界扰动时其控制器表现的性能较为良好，无论是姿态角受到扰动时偏离的角度，还是姿态角受扰动时恢复原姿态角所需的时间都较PID控制表现优异，改进型ADRC控制器在四旋翼无人机的姿态控制受到外界扰动时表现出优异的控制性能；在图10中，三种控制器在四旋翼无人机的高度受到定常扰动控制中，改进型ADRC即使在受到外界或系统内部的定常扰动时，对四旋翼无人机的高度控制几乎无影响，而PID控制器和传统ADRC控制器在四旋翼无人机高度受到扰动的响应中，其受到外界或系统内部的定常扰动时，高度会有一个较大的变换，且受到扰动恢复到定常高度时所需的时间较长，综上所述，PID控制器无论在四旋翼无人机的三个姿态角控制受到扰动中还是在高度控制受到扰动时，其表现出的抗扰动能力均较弱，在受到扰动时候其位置角或高度都会有较大的变化，且恢复到指定的角度或高度时间较长，传统ADRC控制器的控制效果运用于四旋翼无人机定常扰动中，相较于PID会有良好的控制效果，但其无论是恢复时间还是超调仍与理想控制有一定的偏差，改进型ADRC在四旋翼无人机中的定常干扰控制中表现优异，具有较强的抗干扰能力和较强的稳定性。

图11为四旋翼无人机滚转角受到高频扰动的响应曲线，图12为四旋翼无人机受到高频扰动时的高度响应曲线。基于上述实验，图11以滚转角为例当四旋翼无人机受到高频扰动时的姿态角度响应曲线图，图12为四旋翼无人机变高度运行时受到高频扰动的响应曲线。

图11 高频扰动滚转角响应

图12 高频干扰时高度响应

当滚转角做方波运动且受到高频的内部或外部扰动时，从图11中可以得到，PID控制器控制四旋翼无人机滚转角的角度受扰动影响大，当高频扰动一直存在时，角度波动频繁，其鲁棒性和抗干扰能力不强，传统ADRC控制器在控制四旋翼无人机滚转角时，其鲁棒性相较于PID控制器表现的性能较好，但与理想控制器的表现性能仍有一定的差距，改进ADRC在四旋翼无人机滚转角受到高频扰动时其几乎不受外界扰动的影响，且到达预定的角度或高度也较快，在做姿态滚转角运动其抗干扰能力较强，表现性能优异。从图12中可以得到，当四旋翼无人机做变高度运动且受到高频扰动时候，PID控制会让无人机高度运动变化较大且无人机抗扰动性能不佳，传统ADRC受到高频扰动时候波动较小，且高度调节能力强，改进ADRC在四旋翼无人机做变高度运动且受到高频扰动时表示出优异的控制性能，无论是鲁棒性还是超调性及稳定性都表现优异。

从上面实验中可以看出，改进型ADRC无论在四旋翼无人机的三个姿态角控制还是在高度控制中，都表现出优异的控制特性，即使是受到定常扰动时，其稳定性依然很高，当受到高频扰动时，改进型ADRC鲁棒性在三个控制器中表现最强，因此，改进型ADRC符合四旋翼无人机的姿态及位置控制所需的要求。

5 结论

本文针对四旋翼无人机在正常运动时可能出现的各种问题，设计了符合四旋翼无人机姿态及位置的改进型ADRC控制器。通过多方面的实验，验证了改进型ADRC在四旋翼无人机实际应用中的性能，改进后的ADRC相较于PID和传统ADRC拥有更好的表现能力。