一阶电路时域分析教学改革与实践

高文根，陈其工，王冠凌

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

随着我国高教改革的深化，越来越重视培养学生的自主学习能力，在此大环境下，课堂教学学时有了较大的削减[1]，以安徽工程大学“电路分析”课程为例，课堂教学学时被削减了20%。在压缩学时的背景下，为了提高教学效率，实现课时缩减但教学质量不缩水的目标，教学改革势在必行[2]。动态电路分析是电路理论教学体系中的重要内容[3]，通常包括时域分析与频域分析两种分析方法。目前，主流的电路理论教材中一阶电路时域分析法都是按零输入响应、零状态响应、全响应三种情况，分为三个小节来组织教学内容，每小节包含列写电路方程、求解电路方程、讨论物理意义等环节，进而给出三要素分析法[4](P147)，[5](P255)，[6](P221)。这种递进式教学内容组织方式需要有充裕的学时作为保证，此外，一阶电路三种响应的教学内容缺乏数学层面上的归纳统一，不利于学生理解动态电路的物理意义[7]。笔者结合教学中的实践，积极探索学时压缩背景下的电路理论教学模式改革，针对一阶电路时域分析教学中存在的上述问题，探索出一种新的教学方式。从数学层面上实现一阶电路三种响应教学内容的统一，引导学生实现三种响应的融会贯通；采用实际工程案例来加深学生对动态电路的物理意义的理解，激发学生的学习兴趣，培养学生的工程思维。

1 一阶电路的模型

动态电路中通常含有储能元件电容或电感，由于储能元件中的能量吐纳需要一定的时间来完成，当电路换路时，电路由旧稳态过渡到新稳态会产生一个动态响应的过程。动态电路的求解方程为微分方程或积分方程，当电路方程为一阶微分方程时，即为一阶电路[8]。电路模型是电路分析的研究对象，是一阶电路分析的基础，在一阶电路时域分析教学中，首先要建立电路的模型[9](P40)。教学中分别给出具有普适性的结构模型，以及具有统一性的数学模型。

1.1 一阶电路模型的普适性解释

目前，一阶电路时域分析都是在直流激励场景下展开教学，教材中通常采用典型的RC与RL串联电路来进行讲解，实践教学中很多学生存在疑问，基于如此简单的电路结构推导出的三要素公式为什么具有普适性？在实际教学中，依据戴维宁定理推出一阶电路RC串联结构模型，如图1所示，任一线性含源电路网络都可以等效为一个电压源US与电阻R串联电路；为了实现数学方程的统一，方便学生理解与记忆，根据电路理论的对偶原理，依据诺顿定理推出一阶电路GL并联结构模型，如图2所示，任一线性含源电路网络都可以等效为一个电流源IS与电导G并联结构模型。由此，从电路理论层面解释了一阶电路RC串联模型与GL并联模型的由来，给出一阶电路模型具有普适性的依据。

图1 一阶电路RC串联结构模型

图2 一阶电路GL并联结构模型

1.2 一阶电路模型的统一性方程

依据基尔霍夫电压定律列写图1所示RC串联电路的回路电压方程，依据基尔霍夫电流定律列写图2所示GL并联电路的结点电流方程，分别为

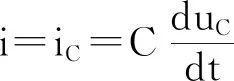
比较式(3)与式(4)可见，RC串联与GL并联一阶电路的方程呈对偶特性，其中RC与GL的乘积为一个常数，统一用τ表示；状态变量电容电压uC与电感电流iL统一用y表示；当一阶电路中激励为直流，电压源US和电流源IS为常数，统一用A表示。一阶电路模型的电路方程可归纳统一为

(5)

式(5)统一了一阶电路的电路方程上，对全响应、零状态响应和零输入响应三种情况都适用，将三种情况归纳在一起讲解，不仅节省了授课学时，提高了课堂效率，而且便于学生从数学层面理解一阶电路问题，易于融会贯通一阶电路的三种响应的教学内容。

2 一阶电路的响应

从数学的角度来看，一阶电路的分析就是求解式(5)所示的一阶微分方程，这对于修完《高等数学》的学生来说，并不是难事。教学中主要侧重于引导学生：推导出三要素公式、理解三要素的物理意义、一阶电路响应的分解，培养学生“工程问题→数学模型→数学求解→工程应用”的工科思维[10]。

2.1 一阶电路的三要素公式

式(5)所示一阶微分方程的全解由其通解yh和特解yp两部分组成，分别为

(6)

其中，k1、k2都为常数，则全解的表达式为

(7)

由式(7)，令t=∞时有k2=y(∞)；令t=0+时有k1=y(0+)-k2=y(0+)-y(∞)。代入式(7)整理得

(8)

其中，y(0+)的物理意义是电路换路后最初时刻y的初始值，对应的是电容电压初始值uC(0+)或电感电流初始值iL(0+)；y(∞)的物理意义是电路换路后重新达到稳定状态时y的稳态值，对应的是电容电压稳态值uC(∞)或电感电流稳态值iL(∞)；τ是个常数，由式(8)可见τ是个时间常数，它的大小影响指数项衰减的快慢，即决定了一阶电路过渡过程时间的长短，工程上一阶电路的过渡过程一般为3τ～5τ。根据上述推导，一阶电路响应的三要素公式可归纳为如式(8)所示，由此，一阶电路分析问题则转化为求解所求响应y的初始值y(0+)、稳态值y(∞)和时间常数τ，求解出三者的数值后，代入式(8)即可得出相应响应的解[11](P36)。

2.2 一阶电路的响应分析

一阶电路的响应分为零输入响应、零状态响应、全响应三种情况，三者都符合式(8)所示的三要素公式，即在数学上是统一的，相互之间的区别仅在于电路变量的初值、有无电源激励的条件不同。教学中根据1.2与2.1两节内容，结合式(5)与式(8)对一阶电路响应进行分析，引导学生实现三种响应的融会贯通。

当一阶电路中没有电源作用，电路的响应仅仅由电感或电容元件的初始储能作用产生，称为零输入响应。此种情况下，电压源或电流源的数值为零，即A=y(∞)=0；电容电压或电感电流的初始值不为零，即y(0+)≠0。代入式(8)可得零输入响应如式(9)所示，可见零输入响应的物理意义是储能元件中储能的放电过程。

(9)

当一阶电路中电感或电容元件没有初始储能，电路的响应仅仅由电源作用产生，称为零状态响应。此种情况下，电容电压或电感电流的初始值为零，即y(0+)=0；电压源或电流源的数值不为零，即A=y(∞)≠0。由式(8)可得零输入响应如式(10)所示，可见零输入响应的物理意义是储能元件在外部电流源激励下的充电过程。

(10)

当一阶电路中储能元件的初始储能和电源都不为零，两者共同作用产生的响应，称为全响应。此种情况下，y(0+)≠0，A=y(∞)≠0，全响应可表示为式(8)，其物理意义是储能元件的储能与外部电源共同作用所产生的过渡过程。由式(8)可见，全响应是由稳态分量(强制分量)y(∞)与暂态分量(自由分量)[y(0+)-y(∞)]e-t/τ叠加的结果。此外，式(8)可以变换为式(11)，则全响应又可理解为由零输入响应和零状态响应叠加的结果。

(11)

3 一阶电路的工程案例

在电路理论教学中，一阶电路的教学内容紧跟在一般线性电阻电路之后，一般电阻电路模型是代数方程，一阶电路模型则是微分或积分方程。这种数学上的跨越是源于电路背后物理本质的不同，如果单纯从理论上讲解，学生难免会觉得抽象，不利于学生理解一阶电路的物理意义，培养学生的工程思维。为了避免理论教学与工程实践脱节，需要结合学生专业特点，选择合适的工程案例进行讲解，引导学生学习一阶电路的物理过渡过程。本文以自动化专业为例，笔者在教学中选用“声光控制路灯电路”作为工程案例，起到了良好的教学效果。

3.1 工程案例电路工作原理

电路理论课程是电类专业的专业基础课，通常在低年级开设，开课时学生还没有学习过其他相关专业课程。因此，需要介绍清楚工程案例电路的工作原理，让学生充分了解工程案例的背景。

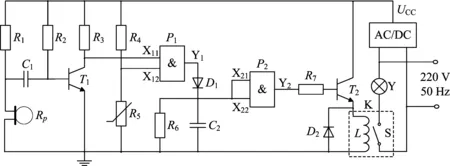
图3 声光控制路灯电路原理图

如图3所示，在“声光控制路灯电路”电路中，AC/DC为直流电源电路，主要功能是将交流电转变为直流电给声光控制路灯系统供电。P1和P2是两个逻辑与门电路，X11、X12、X21和X22分别是它们的输入。R5为光敏电阻，与电阻R4构成分压电路，当光照明亮时，R5阻值很小，使得与门P1输入X12为低电平封锁P1，此时无论P1输入X11的高低，P1输出Y1都为低电平，进而使得与门P2输出Y2为低电平，使得三极管T2截止，继电器K的线圈L不得电，触点S无法闭合，路灯Y不亮。当光照昏暗时，R5阻值很大，使得P1输入X12为高电平，此时P1输出Y1的高低则视X11的高低而定，当没有声音激发拾音器RP时，由于电容C1隔直通交的性质，电源UCC与电阻R2构成三极管T1基极偏置，使得三极管T1工作在饱和区，使得P1输入X11为低电平，其输出Y1为低电平，P2输出Y2为低电平，三极管T2截止，继电器K的线圈L不得电，路灯Y不亮；当拾音器RP受到声音激发时，产生交变信号通过电容C1影响三极管T1基极偏置，造成三极管T1截止，使得P1输入X11为高电平，其输出Y1为高电平，P2输出Y2为高电平，使得三极管T2工作在放大区，继电器K的线圈L得电导通，触点S闭合，路灯Y被点亮。综上所述，只有同时满足环境光线昏暗、拾音器受到声音激发两个条件时，路灯才会点亮，否则路灯不亮，实现了声光控制路灯的功能。

在“声光控制路灯电路”工作原理介绍中，涉及模拟电子电路和数字电子电路两门课程的相关知识，这两门课恰好是电路理论课程的后修课程，教学中应该给予适当的交代，对学生做好引导，激发学生的学习兴趣，培养学生对所学专业的认同感。

3.2 一阶电路工程应用剖析

3.2.1 一阶RC电路

如图3所示，结合3.1节中的工作原理分析，当满足光照昏暗、拾音器受到声音激发时，P1输出Y1为高电平时，二极管D1正向导通，与电容C2构成一阶RC电路给电容C2充电，但拾音器受到声音激发是短暂的，瞬间P1输出Y1就由高电平恢复为低电平，由于一阶RC电路的时间常数τ等于RC的乘积，二极管正向导通电阻很小(电阻阻值R6被设计的很大，可以近似忽略视)，此时时间常数τ很小，瞬间电容C2已被充满，使得P2输出Y2为高电平，进而驱动继电器K的触点S闭合，路灯Y被点亮。

当P1输出Y1由高电平恢复为低电平后，二极管D1反向截止，此时电阻R6和电容C2构成一阶RC电路供电容C2放电，由于R6阻值很大，此时时间常数τ很大，电容放电过渡过程相对缓慢，实现在一定时间内能维持P2的输入X21和X22为高电平，即能维持P2输出Y2为高电平，起到路灯延时照明的作用，延时长短可以通过R6和C2的参数来设计。

3.2.2 一阶GL电路

当P2输出Y2为高电平时，使得三极管T2工作在放大区，三极管T2与继电器K的线圈L构成一阶GL电路，由于一阶GL电路的时间常数τ等于GL的乘积，此时三极管的等效电导G较小电阻，时间常数τ较小，线圈L快速充电，令触点S闭合，点亮路灯Y。当电容C2经R6放电使得P2输出Y2变为低电平，三极管T2截止，根据电感的特性，其电流不允许突变，所以在线圈L两端设计了并联二极管D2，该二极管作用是供三极管T2截止后线圈L续流，释放线圈储存的能量，避免线圈L两端产生过电压，损坏电路器件。由于二极管D2正向导通的电导较大，此时时间常数τ较大，电感释放能量过程较长，冲击较小。

4 结论

将一阶电路的各个响应从数学模型上进行统一，归纳在一起列写电路方程、求解电路方程、讨论物理意义，从数学上推导出三要素公式，同时阐明三要素的物理意义，再从不同角度理解一阶电路各种响应的本质，以及相互之间的关系。此外，结合工程实例讲解一阶电路的过渡过程特性，引导学生认识一阶电路在工程中的应用，让学生进一步理解一阶电路动态响应的物理意义。通过教学实践发现，与原有的教学方式相比，本文提出的一阶电路时域分析教学方法可减少三分之一的教学课时，教学效果良好，适应课时缩减的教学需要，对新工科背景下高校电路理论课程的教学具有一定的参考意义。