提高储层平均毛管力曲线计算精度的分形方法

李 竞，朱国金，刘 晨，王兴龙，王 龙.

(1.海洋石油高效开发国家重点实验室，北京 100028；2.中海油研究总院有限责任公司，北京 100028；3. 中国海洋石油国际有限公司，北京 100028)

0 引言

储层岩石的微观孔隙结构极端复杂，很难精确描述。孔隙度、渗透率、RQI等从不同角度定量表征孔隙结构，毛管压力曲线和J函数曲线定量反应流体在多孔介质渗流过程中的压力和饱和度变化关系。用毛管压力函数(或J函数)分别拟合同一类储层的单个岩心的毛管压力曲线(J函数曲线)，对拟合参数做平均，再代回函数式就可求出代表该类储层微观孔隙结构平均化性质的平均毛管压力曲线(平均J函数曲线)，以用于油藏数值模拟，其中，平均曲线的计算精度取决于每个岩心的曲线拟合精度。

目前广泛应用于常规孔隙分选较好储层的无因次毛管压力即J函数幂率回归式是经验公式，国外称之为Brook Coery经验回归式[1-4]，相关参数未明确指明与岩心孔隙结构参数的关系，对大量孔隙分选差的储层，还存在实测毛管力曲线拟合精度偏低的问题。基于分形理论和毛管束渗流模型，李克文推导出现有幂函数的表达式并将参数与分形维数建立了关系[4]，指出了幂函数的适用条件是分形维数D<3和残余润湿相饱和度边界条件下毛管压力Pc趋于正无穷大，此外还推导出广适分形毛管力函数[1]，但在该函数中，润湿相饱和度进行了归一化，即代表可采储量采出程度，这导致残余润湿相饱和度边界点处，超出负指数幂函数自身的定义域而无法计算。贺承祖[5]通过将达西定律和泊稷叶定律联立，也推导出幂函数回归式，区别是润湿相饱和度不进行归一化，即代表累计产油量，残余润湿相饱和度边界点处不存在数学问题。目前毛管压力函数中是否对润湿相饱和度进行归一化，尚存在争议，但前人研究表明，储层孔隙结构至少在一定孔喉半径范围内，确实具有分形特征[5]，可以用分形方法对现有经验公式进行解释和改进。

该文通过考虑孔隙分选差储层在小孔喉方向集中程度更高，推导出无因次毛管压力J函数的分形回归式，是对李克文广适毛管力回归式的推广和修正(润湿相饱和度不做归一化处理)。伊拉克低渗灰岩储层的实测J函数数据证实，该方法能有效提高拟合精度。对于孔隙分选较好的储层(例如渤海高渗砂岩气层)，可继续使用现有分形幂率型回归函数，而分形参数则指出了回归结果与分形维数、最大、最小毛管压力的关系。分形毛管压力(J函数)式的提出，从多孔介质渗流角度，进一步深化了复杂的微观孔隙结构定量表征，针对分选较差的储层，分形式可反算出精度较幂率型更高的毛管压力曲线，有效提高该类储层平均毛管压力曲线的计算精度。

1 J函数分形回归式的数学推导

无因次毛管压力即J函数幂率回归经验公式，国外称之为Brook Coery经验回归式[1-4]。

(1)

式中:J(Sw)为无因次毛管压力函数，无因次；A0，B0为经验回归系数，无因次；Sw为润湿相饱和度，小数。

根据分形几何理论[1]和不等径等长平直毛管束渗流模型[6]，自相似的单元体可以无限填充符合分形结构的储层微观孔隙空间，该自相似体可为半径为变量r，长度为常量L的平直毛细管[1]。压汞过程中，某个汞饱和度增加区间，汞新填充的一簇毛细管的数量N(r)与其半径r之间存在幂函数关系[7]:

N(r) =ar-D

(2)

式中:N(r)为某时刻汞新填充的半径为r的毛细管数量，根；r为某时刻被汞新填充的毛细管的半径，μm；D为分形维数，无因次；a为比例常数，无因次。

考虑孔隙分布的连续性，则压汞岩心的总孔隙体积为:

(3)

式中:V(r)为岩心总孔隙体积，μm3；L为岩心长度，μm；rmin为孔隙中最细毛细管对应的半径，μm；rmax为孔隙中最粗毛细管对应的半径，μm。

由式(3)易得某时刻未被汞充填的即半径小于r的孔隙累积体积[5]为：

(4)

同理可得已被汞充填的即半径大于等于r的孔隙累积体积为:

(5)

该时刻润湿相饱和度，即空气相饱和度为:

(6)

毛管压力与孔隙半径的关系式为:

(7)

式中:σ为汞-空气界面张力，N/m，一般取0.48 N/m；θ为汞-空气润湿角，(°)，一般取140°；Pc为毛细管压力，MPa。

式(7)代入式(6)，可得:

(8)

若用SHg= 1 -SAir替换为含汞饱和度，则式(8)变为式(9):

(9)

式(8)、式(9)中:Pmax为最小毛管半径对应的最大毛管压力，Pe为排驱压力，即最大毛管半径对应的最小毛管压力。

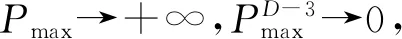
(10)

(11)

式(10)或式(11)即贺承祖压汞分形函数[5]，与Brooks Corey函数[1]相比，饱和度未做标准化处理，由于分形维数D<3，则归一化饱和度为0的点，超出幂函数幂指数为负数时的定义域而无法计算，故贺承祖压汞分形函数式(10)或式(11)更合理。

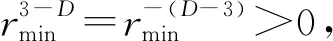
(12)

由式(9)可得:

(13)

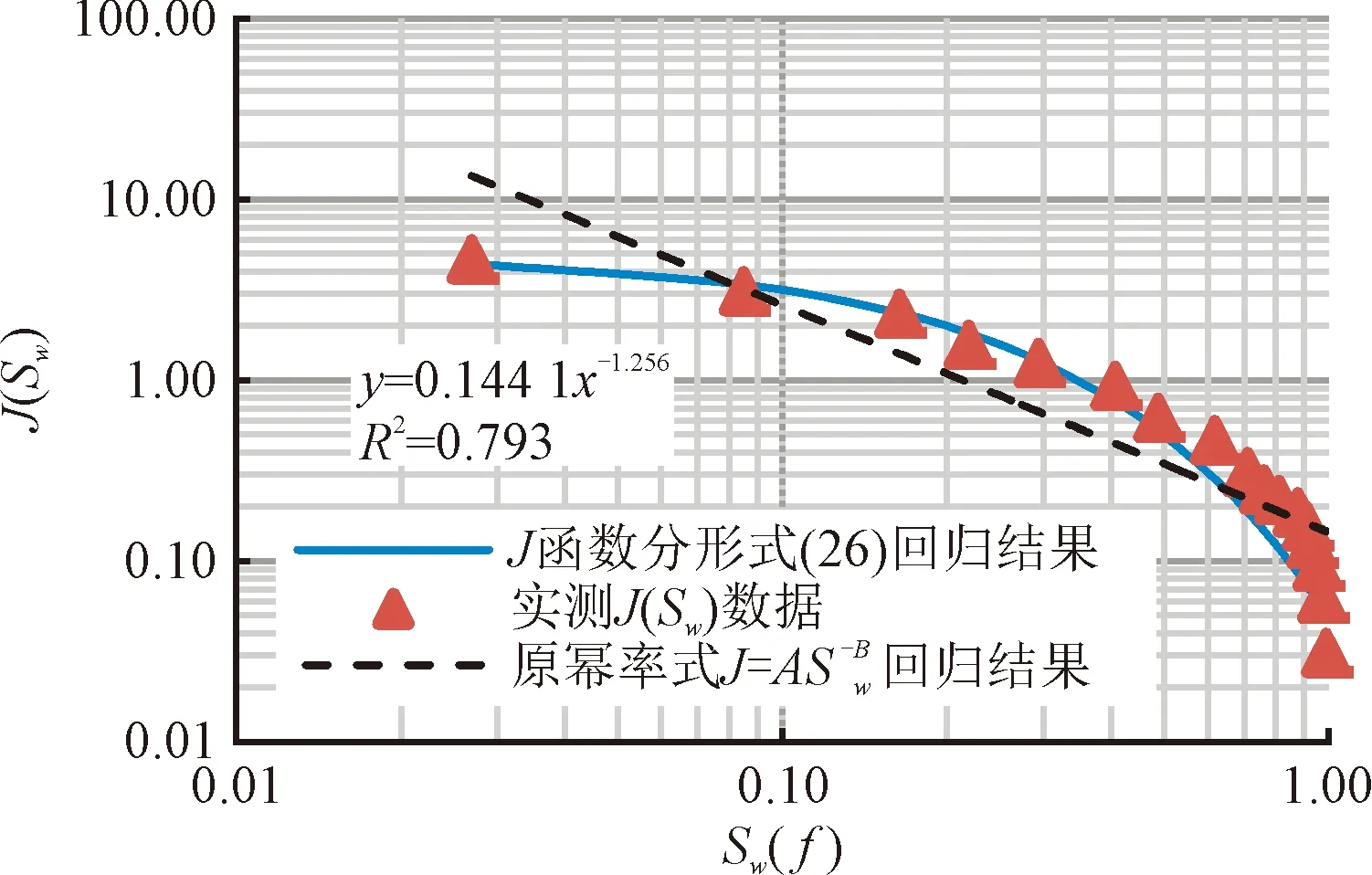
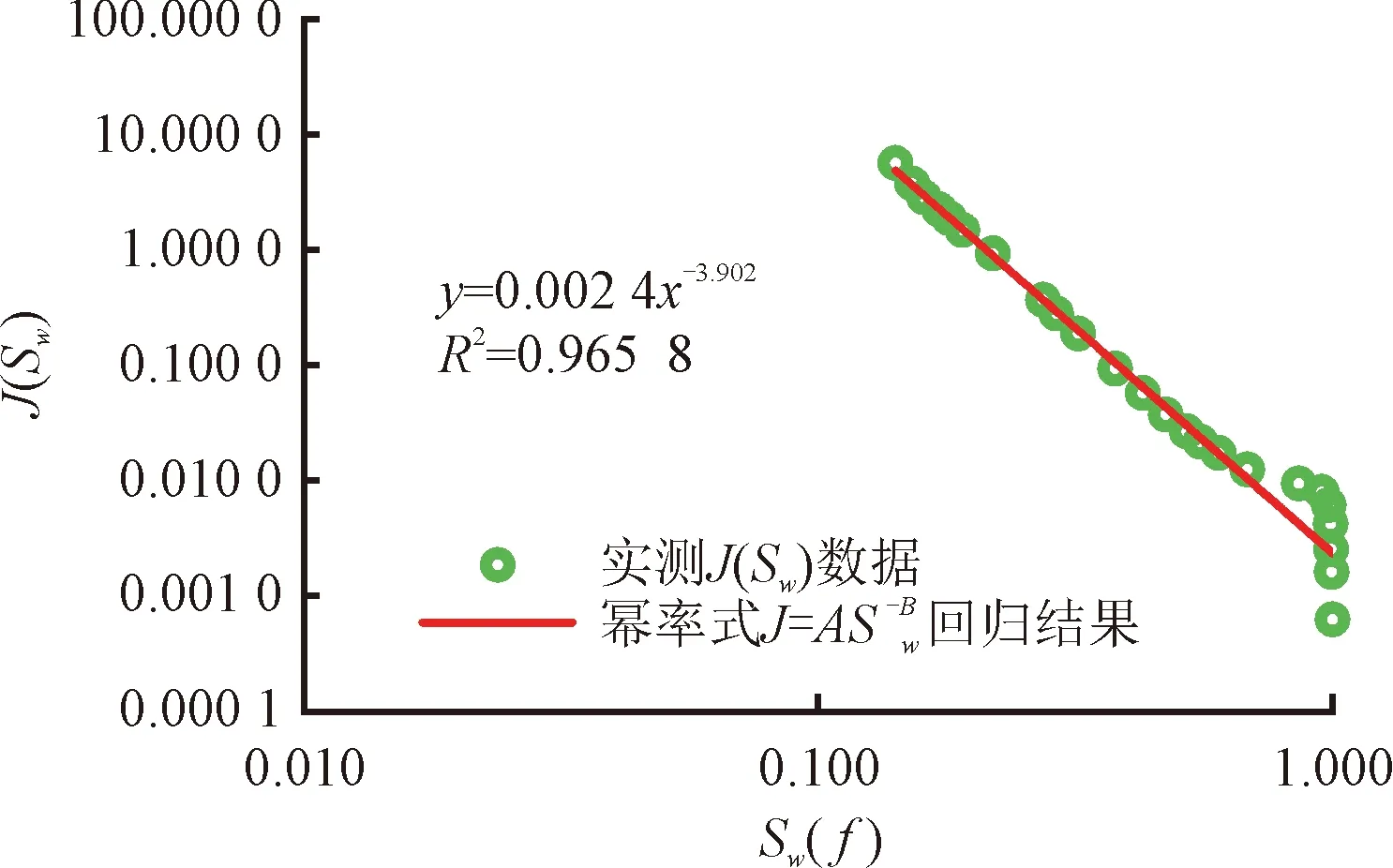
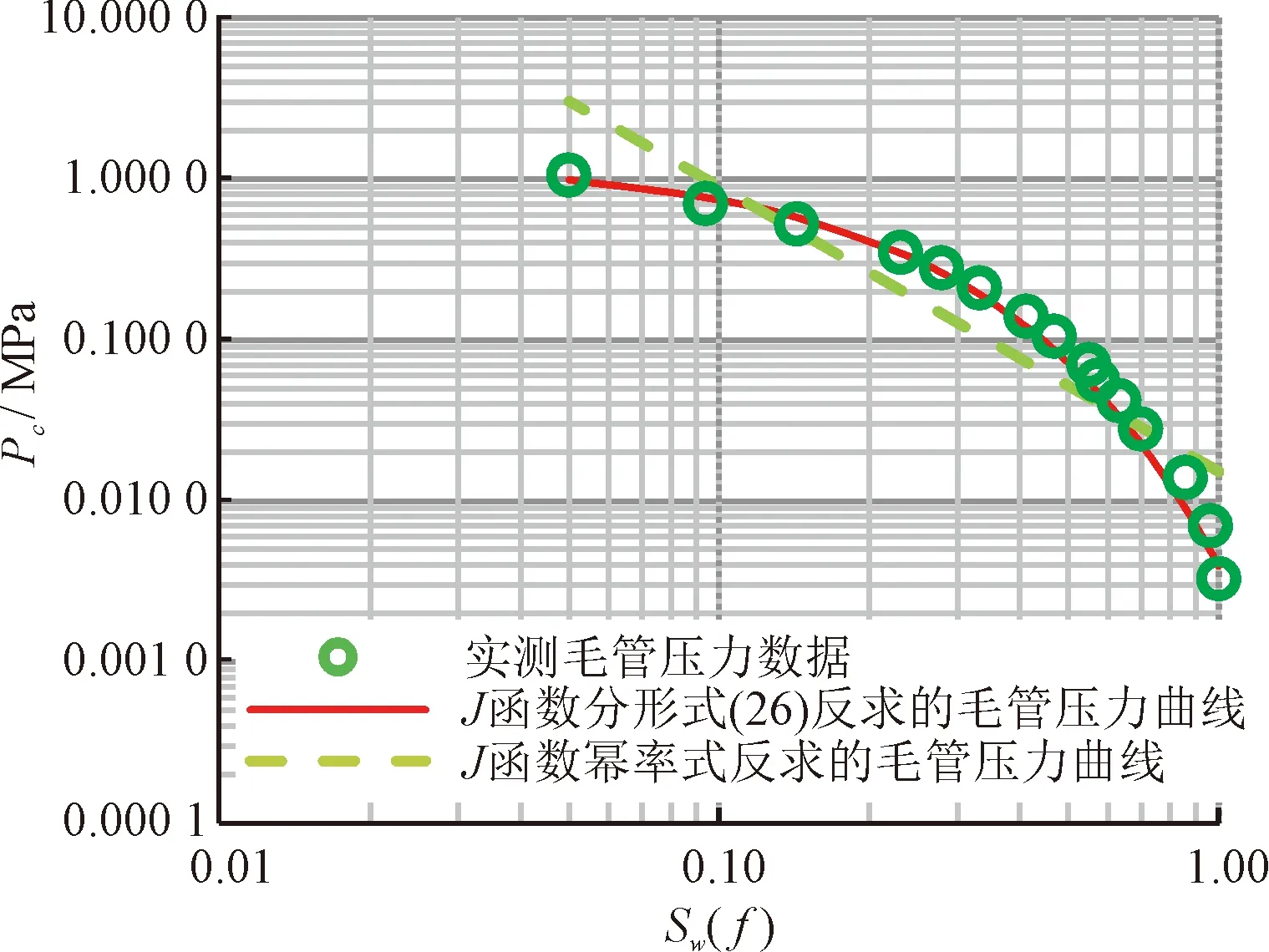
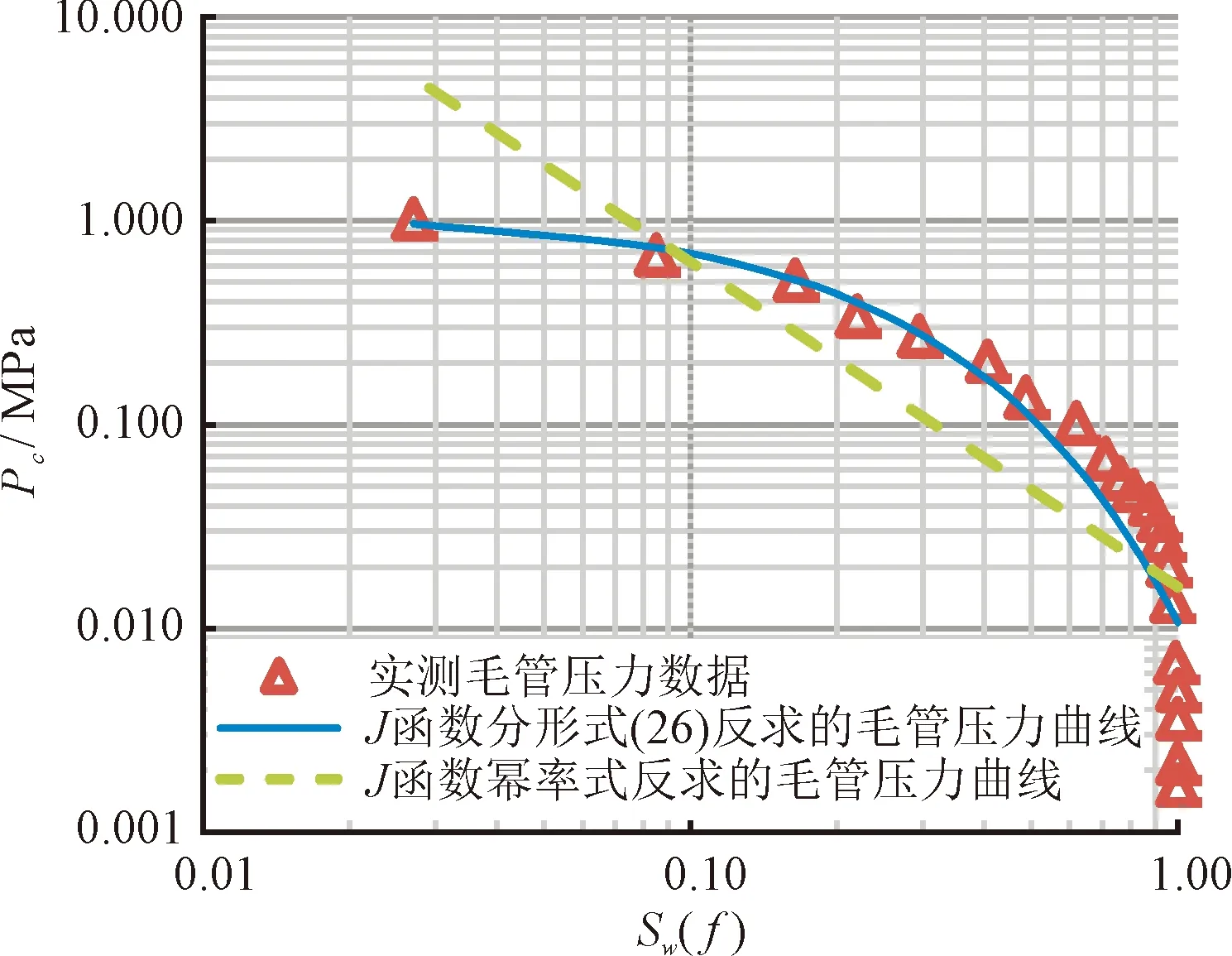
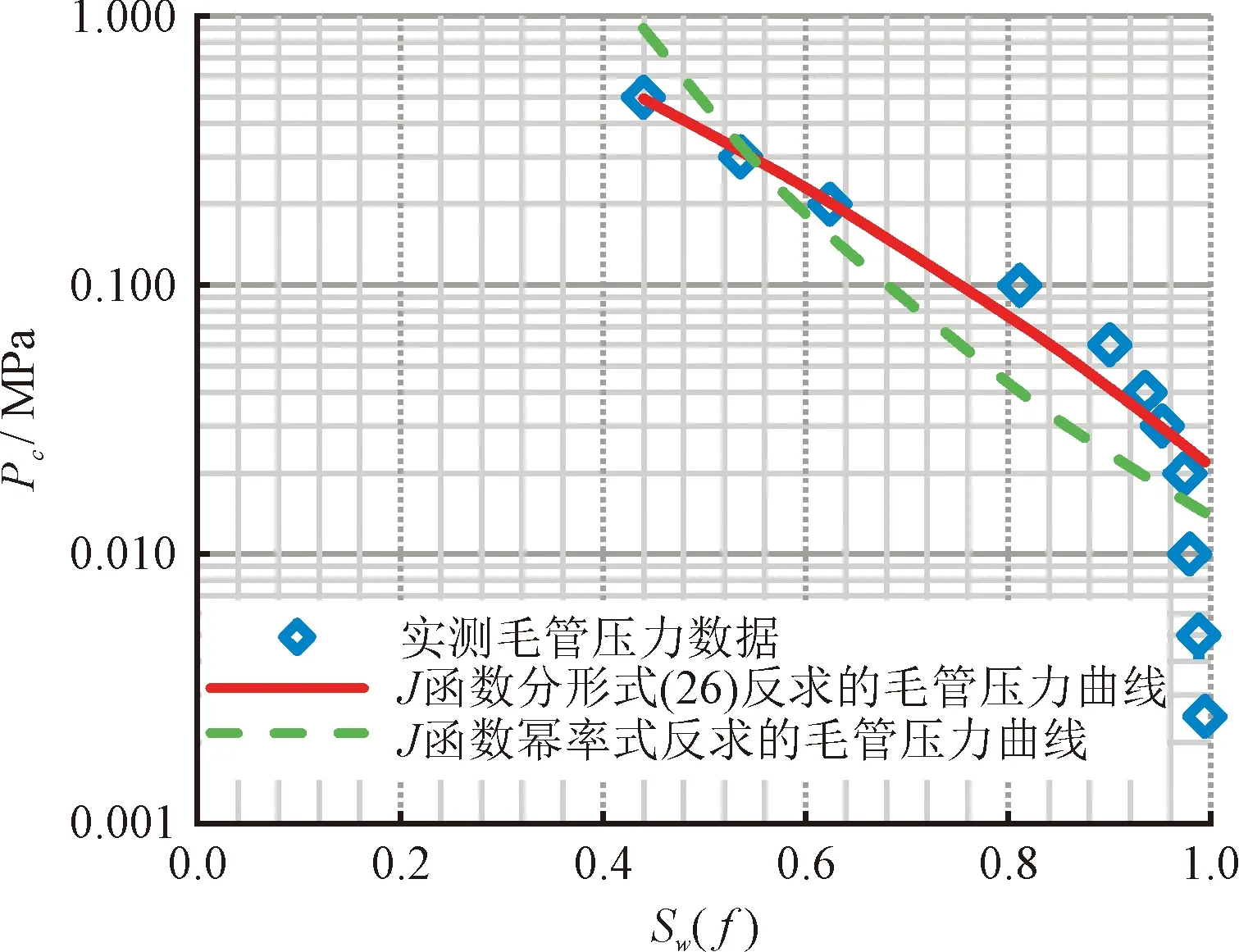
式(12)或式(13)为压汞分形函数回归式在3

根据不等径等长毛管束渗流模型和泊稷叶定律，在Δp的压差下，黏度为μ的汞通过单根毛细管的流量为:

(14)

式中:qHg为半径为r的单根毛细管中汞的流量，mm3/s；r为单根毛细管半径，μm；Δp为驱替压差，MPa；μ为汞相黏度，mPa·s；L为毛细管长度或岩心长度，μm。

将单根毛管体积V(r) =πr2L代入式(14)，得:

(15)

从rmin至rmax加和得到多孔介质总流量为:

(16)

将汞累计充填的毛细管体积用岩心含空气饱和度表示为:

(17)

式(17)中:V(r)为单根毛细管体积，μm3；A为岩心截面积，μm2；L为岩心长度，μm；φ为岩心孔隙度，小数；SAir为岩心含空气饱和度，小数。

将式(17)代入式(16)，得:

(18)

联立达西定律:

(19)

得到绝对渗透率的表达式，并考虑孔隙的连续分布，得到:

(20)

J函数定义为无因次毛管力，并消除孔隙度和渗透率的影响:

(21)

式中:σ为界面张力，N/m；θ为润湿角，(°)；Pc为毛细管压力，MPa；k为绝对渗透率，μm2；φ为孔隙度，小数。

对于常规中、高孔渗且孔隙分选好的储层，将式(7)、式(10)、式(20)代入式(21)，可得:

(22)

实际应用时，暂不纠结于各参数内在的相关性，式(22)简化为:

(23)

式中:A0为分形维数相关拟合参数，无因次，A0>0；B0为分形维数相关拟合参数，无因次，B0>0；SAir为含空气饱和度，小数，0

式(23)即目前广泛应用的J函数幂率型经验回归式[6]，通过推导，揭示出其应用条件是分形维数D<3和残余空气饱和度下rmin→0，该式将经验参数A0，B0与分形维数建立了关系。

对差分选的低孔、低渗储层，将式(8)、式(12)、式(20)代入式(21)得:

(24)

而若代入式(12)而非式(13)，将得到:

(25)

式(24)和式(25)可分别简化为:

(26)

(27)

式中:A1，A2为分形维数、最大、最小毛管压力相关拟合参数，无因次，A1>0，A2>0；B1，B2为最大、最小毛管压力相关拟合参数，无因次，00，C2>0；SAir为含空气饱和度，0

式(26)或式(27)即J函数分形回归式在30，故该式的应用条件是30。

另外需要指出的是，与流体性质相关的润湿角、界面张力，在推导过程中均被消去，即J函数分形回归式(23)、式(27)不仅适用于压汞过程，也适用于任意两相流体的驱替过程，式(23)等同于式(1)，下文统称式(23)、式(1)为分形幂率式。

2 分形J函数回归式提高差孔隙分选储层的回归精度

通过以上对储层岩心J函数分形数学公式的推导，明确了幂率型J函数回归式的分形物理意义和变化范围，其能在孔隙分选好的中高渗储层中广泛应用的原因是该类储层分形维数D<3，rmin≪rmax，孔隙半径主要集中在大于rmin的范围，压汞至残余空气饱和度时，rmin→0；其在孔隙分选较差的低渗储层中回归精度偏低的原因是该类储层分形维数30，新分形式(26)或式(27)的形式发生变化。

图1～图3为某碳酸盐岩油藏低渗灰岩储层实测J函数数据，由于双对数图上的线性特征，可知分形幂率式(23)的回归精度无法进一步提高，而新分形式(26)或式(27)则可明显提高，使用式(26)计算的分形维数结果均大于3、小于5。以伊拉克AG油田低渗灰岩油层(图3)为例，回归参数C1=7.152 0，由式(26)，分形维数D=3+1/C1=3.139 8。由表1知，表征回归精度的确定性系数R2提高0.157 1～0.248 2，平均提高0.20，均达到0.99，详见表1。

图1 伊拉克BU油田低渗灰岩油层J函数拟合Fig.1 J function matching for low permeability limestone oil layer in BU oilfield，Iraq

图2 伊拉克FQ油田低渗灰岩油层J函数拟合Fig.2 J function matching for low permeability limestone oil layer in FQ oilfield， Iraq

图3 伊拉克AG油田低渗灰岩油层J函数回归Fig.3 J function matching for lowpermea bility limestone oil layer in AG oilfield， Iraq

表1 J函数曲线样品物性参数和回归参数表Table1 Physical properties and J function matching parameters of rock samples

图4为某高渗砂岩气层实测J函数数据，在双对数图上呈现线性特征，分形幂率式(23)的精度已足够高，回归参数B0=3.902 0，确定性系数0.965 8，由式(21)，分形维数计算为3-1/3.902 0=2.744 0。

图4 渤海某油气田高渗砂岩气层J函数回归Fig.4 J function matching for high permeability sandstone gas layer in Bohai oilfield， China

分形维数的获取，除了用分形式(22)或式(25)通过实测J函数曲线回归得到外，还可以通过毛管压力分形函数式(9)和式(11)对毛管压力曲线回归得到，此外，还可以用相对渗透率分形函数对相渗曲线回归得到，有学者对实际岩心薄片进行作图法测定[8]分形维数，该文只讨论第一种方法。

3 求取平均毛管压力曲线

对同一类储层单个岩心J函数拟合指数求平均，就可求取代表该类储层平均毛管压力曲线。图5～图7分别是伊拉克BU，FQ，AG油田差分选、低渗灰岩油层单个样品由J函数新分形式(26)和幂率式(23)反求出的毛管压力曲线对比，图8是渤海某油气田高渗气层求出的平均毛管压力曲线，幂率式(23)反求的结果合理。可见对该类储层， 新分形式(26)反求出的毛管压力曲线精度更高，幂率分形式(23)精度明显损失较多。

图5 伊拉克BU油田低渗灰岩油层反求毛管压力Fig.5 Average capillary pressure curve of low permeability limestone oil layer in BU oilfield， Iraq

图6 伊拉克FQ油田低渗灰岩油层反求毛管压力Fig.6 Average capillary pressure curve of low per permeability limestone oil layer in FQ oilfield， Iraq

图7 伊拉克AG油田低渗灰岩油层反求毛管压力Fig.7 Average capillary pressure curve of low permeability limestone oil layer in AG oilfield， Iraq

图8 渤海某油气田高渗气层平均毛管压力曲线Fig.8 Average capillary pressure curve of high permeability sandstone gas layer in Bohai oil field，China

从图5～图8可以看出，无论是J函数新分形式(26)还是幂率式(23)，在大孔隙段拟合效果均不太理想，这是由于毛管压力测试过程中的麻皮效应导致[6]，即压汞初期测试点反应岩样表面凹凸不平的孔，未反应孔隙结构的分形特征。

4 结论

1)基于分形理论，推导出现有J函数幂率式的经验回归系数与分形维数的关系，该式的适用条件是分形维数小于3和残余润湿相饱和度下最小毛细管半径趋于0，解释了其广泛适用于中高渗岩心的原因；

2)基于分形理论，推导出适用于差孔隙分选储层的J函数分形表达式，其适用条件是分形维数大于3并小于5，残余润湿相饱和度下最小毛细管半径大于0，对应该类储层的孔喉分布特征，通过实测数据证实分形表达式和参数范围控制可以有效提高该类岩心或储层的J函数回归精度，确定性系数R2平均可提高0.20，达到0.99；

3)针对孔隙分选差的储层，J函数分形式的新分形式反求出的单个样品毛管压力曲线精度较幂率型损失小，从而能够有效提高该类储层多个岩心样品的平均毛管压力曲线的计算精度。