考虑压敏效应的技术极限井距计算方法研究

李承龙

(1.中国石油大庆油田有限责任公司 勘探开发研究院，黑龙江 大庆 163712；2.黑龙江省油层物理与渗流力学重点实验室，黑龙江 大庆 163712)

0 引言

特低渗透油藏储层物性差，渗透性差[1-5]。流体满足低速非达西渗流，渗流阻力大[6-8]。油层受压敏效应影响严重，渗透率损失严重，启动压力梯度增加，加剧了建立有效驱替的难度，导致开发效果及效益差[9-12]。井网加密是改善油藏开发效果的重要调整措施，注采井距过大，渗流阻力大，注采井间压力消耗大，无法建立有效驱替；注采井距过小，开发成本增加，效益变差[13-14]。因此，针对特低渗透油藏地质条件及开发技术政策，采用合理注采井距对油藏的有效开发具有极重要的意义。

针对特低渗透油藏，传统技术极限井距计算方法存在两点不足，一是未考虑压敏效应对注采井间驱替压力分布的影响[15-18]，二是未考虑压敏效应引起启动压力梯度发生动态变化的问题[19-20]，导致此类方法不符合特低渗透油藏矿场实际情况。为满足开发需求，该研究首先建立了考虑压敏效应的单井产量计算公式，根据公式分析压敏效应对注入井和采油井井底附近驱替压力(边界供给压力与井底压力之差)的影响，其次建立了基于压敏效应的变启动压力梯度计算公式，明确地层压力对启动压力梯度的影响。结合传统计算公式，推导考虑压敏效应的技术极限井距计算公式，形成适用于特低渗透油藏的技术极限井距计算方法，为油田的开发调整提供技术保障。

1 考虑压敏效应的驱替压力计算公式

考虑到渗透率的压力敏感性，将渗透率与压敏系数关系式带入到单井产量计算公式，积分得到考虑压敏效应产量计算公式[21]:

(1)

式中:K0为原始渗透率，mD；M为压敏系数，MPa-1；K为当前地层压力下的渗透率，mD；ph为供给压力，MPa；rh为供给半径，m；rw为井半径，m。

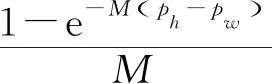
油井产量

(2)

水井产量

(3)

即:

(4)

由式(2)和式(4)，油水井附近的驱替压力分别为:

油井附近驱替压力

(5)

水井附近驱替压力

(6)

式中:Mo为采油井井底附近储层压敏系数，MPa-1；Mw为注入井井底附近储层压敏系数，MPa-1；ΔP1为采油井附近驱替压力，MPa；ΔP2为注入井附近驱替压力，MPa。

考虑压敏效应条件下的注采井间驱替压力可表示为:

(7)

为了简化问题，令ph=pi，则上式可整理为:

(8)

2 考虑压敏效应的启动压力梯度计算公式

将渗透率与压敏系数关系式带入到流度与启动压力梯度关系式[22]，得到的基于压敏效应的变启动压力梯度计算公式为:

(9)

根据上式可知，与传统认识相比，考虑压敏效应条件下的启动压力梯度是动态变化的，与流度、压敏系数、原始地层压力及目前地层压力有关。

3 考虑压敏效应的技术极限井距计算公式

传统技术极限井距计算公式为:

(10)

其中:

ΔP=Pe-Pw

(11)

式中:ΔP为驱替压力，MPa；R为技术极限井距，m；Pe为注入井井底压力，MPa；Pw为采油井井底压力，MPa。

将式(7)、式(8)和式(9)带入式(10)，得到基于压敏效应的变启动压力梯度技术极限井距计算公式为:

(12)

通过对比分析，传统计算公式仅考虑了驱替压力、静态启动压力梯度与井距的关系；该文所建立技术极限井距计算公式中考虑因素全面，包括原油流度、原始地层压力、目前地层压力、基于压敏效应的驱替压力等因素，可完善地描述特低渗透油藏储层及开发特征。

当不考虑压敏系数时，式(12)两端可整理为:

(13)

求极限并化简可得到:

(14)

进一步整理得到式(10)，证明公式推导过程的准确性。

4 模型参数分析

以大庆长垣外围肇源油田Y-4区块为例，利用所建立模型分析渗透率、注采压差、地层压力保持水平、原油黏度及压敏系数与极限注采井距的关系。截至2019年底，Y-4区块渗透率为1.5 mD，地下原油黏度为9.3 mPa·s，原始地层压力为14.8 MPa，目前地层压力7.3 MPa，破裂压力为13.3 MPa，注水井注水压力为13.3 MPa，油井井底流压为2.6 MPa，埋深为1 002 m，井筒半径为0.127 m，启动压力梯度为0.152 3 MPa/m，采油井端压敏系数为0.035 6/MPa，注水井端压敏系数为0.035 6/MPa。肇源油田渗透率与启动压力梯度的关系见式(15)，渗透率与压敏系数关系见式(16)和式(17)。

λ=0.221K-0.857

(15)

采油井端渗透率与压敏系数关系

Mo=0.043 2e-0.129 8K

(16)

注水井端渗透率与压敏系数关系

Mw=0.004 3e-0.129 8K

(17)

4.1 渗透率与技术极限井距关系

图1为渗透率与技术极限井距关系曲线。随着渗透率的变大，技术极限井距逐渐变大。渗透率越大，启动压力梯度越小，压敏效应影响越小，利用新方法计算的技术极限井距越大，越容易建立有效驱替；当渗透率小于2 mD时，渗透率与技术极限井距呈非线性变化，渗透率大于2 mD时，二者呈近似线性变化；与传统方法计算结果相比，利用新方法计算的技术极限井距进一步减小6～20 m，平均减小16 m。

图1 渗透率与技术极限井距的关系曲线Fig.1 Relationship curve between permeability and technical limit well spacing

4.2 地层压力保持水平与技术极限井距关系

图2为地层压力保持水平与技术极限井距关系曲线。地层压力保持水平对传统方法计算结果没有影响，与该文推导公式计算结果呈正相关；地层压力保持水平越高，压敏效应影响程度越弱，渗透率损失越小，启动压力梯度增幅越小，地层能量越充足，利用新方法计算的技术极限井距越大；地层压力保持水平与技术极限井距呈线性关系；当地层压力保持水平为70%时，与传统方法相比，采用新方法计算结果为34.6 m，技术极限井距需要进一步缩小10.4 m，当地层压力保持水平为100%时，采用新方法计算结果为40.2 m，技术极限井距需要进一步缩小4.8 m。为了实现有效驱替，特低渗透油藏需要保持较高的地层压力保持水平。

图2 地层压力保持水平与技术极限井距的关系曲线Fig.2 Relationship curve between formation pressure retention level and technical limit well spacing

4.3 注入压力与技术极限井距关系

图3为注入压力与技术极限井距关系曲线。注入压力越高，注采压差越大，驱替压力越大，技术极限井距越大，越容易形成有效驱动体系；注入压力与技术极限井距呈线性关系，随着注入压力的增大，采用新方法计算结果增幅较小；与传统方法计算结果相比，利用新方法计算的技术极限井距进一步减小10～13 m，平均减小11 m。特低渗透油藏可通过提高注入压力实现有效开发。

图3 注入压力与技术极限井距的关系曲线Fig.3 Relationship curve between injection pressure and technical limit well spacing

4.4 采油井井底流压与技术极限井距关系

图4为采油井井底流压与技术极限井距关系曲线。采油井井底流压越大，注采压差越小，驱替压力越小，能量损失越严重，所需技术极限井距越小；采油井井底流压与技术极限井距呈线性关系；与传统方法计算结果相比，利用新方法计算的技术极限井距进一步减小9～14 m，平均减小11 m。降低采油井井底流压，更容易建立有效驱替。

图4 采油井井底流压与技术极限井距的关系曲线Fig.4 Relationship curve between bottomhole flow pressure and technical limit well spacing

4.5 压敏系数与技术极限井距关系

压敏系数是表征储层压力敏感程度的物理量，压敏系数越大，压敏效应越强，储层渗透率变化越明显。图5为压敏系数与技术极限井距关系曲线，压敏效应对传统方法计算结果无影响；压敏效应越大，渗透率损失越大，启动压力梯度越大，利用新方法计算技术极限井距越小，区块越不易形成有效驱动体系；压敏效应与技术极限井距呈非线性关系；与传统方法计算结果相比，利用新方法计算的技术极限井距进一步减小3.5～18 m，平均减小11.3 m。

图5 压敏效应与技术极限井距的关系曲线Fig.5 Relationship curve between pressure sensitive effect and technical limit well spacing

4.6 启动压力梯度与技术极限井距关系

图6为启动压力梯度与技术极限井距关系曲线。启动压力梯度对技术极限井距影响较大，启动压力梯度越大，技术极限井距越小，两者呈非线性关系。启动压力梯度越大，渗流阻力越大，建立有效驱替难度越大。与传统方法计算结果相比，利用新方法计算的技术极限井距进一步减小11.4～15.2 m，平均减小11.8 m。

图6 启动压力梯度与技术极限井距的关系曲线Fig.6 Relationship curve between starting pressure gradient and technical limit well spacing

5 实例计算与分析

为了实现有效驱替，改善Y-4区块开发效果，2018年7月采取油水井对应压裂措施，根据传统技术极限井距计算结果(64 m)，优化设计压裂规模，压后注采井两端裂缝间距为50～72 m，区块初期吸水能力较强，但注入压力呈快速上升趋势，而注入量持续下降，区块仍未建立有效驱替。

利用新公式计算结果为47 m，小于区块实际井距。2019年11月，根据技术极限井距计算结果，重新优化设计压裂规模，选取1个井组实施二次压裂措施，压后该井组注入能力大幅度提升，产量明显增加，由4.8 m3/d上升至6.0 m3/d，注入压力由15.3 MPa下降至12.6 MPa，井组日产油量由1.7 t/d上升至4.6 t/d，日产液量由2.8 t/d上升至6.6 t/d，截止至2020年3月，该井组日产液量为5.7 t，证明该井组在二次压裂后已形成有效驱替。表1结合矿场实际情况，验证了该文所建公式计算结果更符合矿场实际情况。

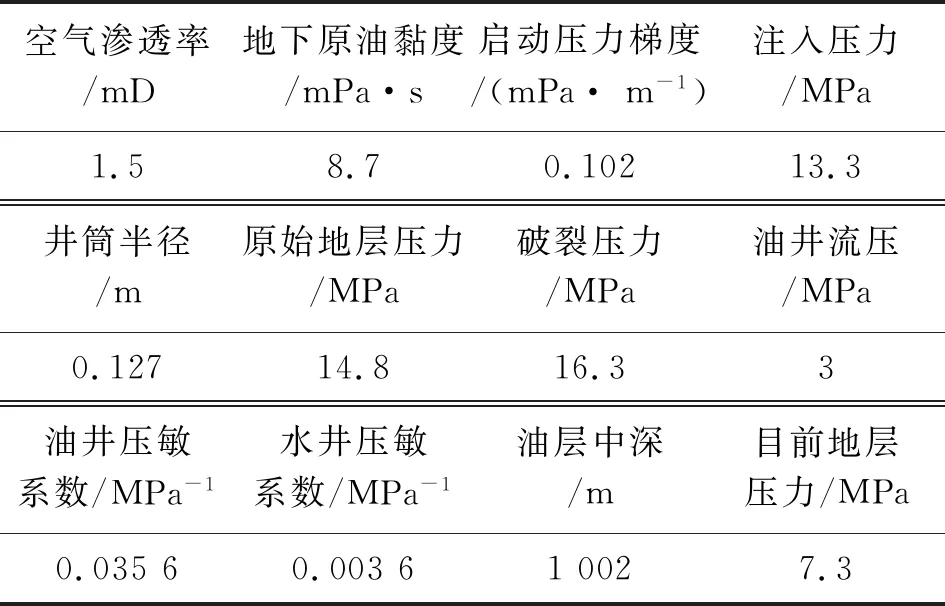
表1 Y-4区块基本参数统计表(2018.7)Table 1 Statistical table of basic parameters of block Y-4

图7为Y-4-W1注入井生产曲线。

图7 Y-4-W1注入井生产曲线Fig.7 Y-4-W1 injection well production curve

表2为Y-4-W1井组压裂前后生产情况。

表2 Y-4-W1井组压裂前后生产情况Table 2 Production situation of well group Y-4-W1 before and after fracturing

6 结论

1)利用考虑压敏效应的渗透率计算公式及启动压力梯度计算公式，推导了考虑原始地层压力及目前地层压力的启动压力梯度计算公式；利用考虑压敏效应的单井产量计算公式，建立了注采井附近的驱替压力计算公式。

2)通过分析所建模型参数得出，渗透率越大，注入压力越大，地层压力保持水平越高，采油井井底流压越小，压敏效应影响越小，技术极限井距越小，启动压力梯度越大，越容易建立有效驱替。

3)与传统方法计算结果相比，考虑压敏效应条件下，该文所建模型计算技术极限井距需进一步缩小3.5～20 m，平均缩小10 m以上。

4)Y-4-W1井组根据该文计算结果优化设计压裂规模后，注入能力及生产能力明显改善，动态数据证明了该井组已经成有效驱动体系。