缓冲/行走一体化着陆器运动学研究与步态规划

贾 山，周向华，陈金宝，赵建华，张 胜

(1. 南京航空航天大学航天学院，南京 211106；2. 航天进入减速与着陆技术实验室，南京 211106；3. 深空星表探测机构技术工信部重点实验室，南京 211106)

0 引 言

着陆缓冲可靠性及巡视探测灵活性是月球探测中备受关注的重要问题[1-2]。目前，国内外星表着陆装置普遍采用腿足式构型和固定式着陆设计，着眼点仅限于安全稳定地实现落震吸能，要求着陆点必须处于尽可能平坦的区域，且只能通过释放轮式巡视器的方式来实现对着陆器周边有限区域的探测，存在着难以实现主动可调姿式着陆缓冲、探测范围可扩展性不足、难以为月球基地建设任务提供配套设施和支持等局限性，需要研制一种具备姿态调整和位置移动等功能的着陆器[3]。

在可行走着陆器领域，国内外尚未有成功的任务案例，只在理论和工程方面，进行了一些探索性的研究和设想。2004年，Lockheed Martin公司参与NASA的探索系统体系研究，提出了轮式驱动的可移动着陆器设想[4]；同年，Boeing公司提出了一种火星探测器方案，包含一个载人着陆器和三个货运着陆器，载人着陆器采用传统腿足式构型不可移动，货运着陆器采用轮腿式构型可在星表移动并承担居住和探测任务[5]；NASA在星座计划下论证了可移动着陆器的优点和应用前景，并基于轮腿式移动系统ATHLETE提出了可移动月球着陆器的方案设想[6]。文献[3]对可移动月球着陆器在月球探测中的任务进行分析，指出移动式月球着陆器在月球探测、月表越障、月球基地建设维护和月球基地转移重建等任务中具有显著优势；文献[7]对新一代载人月面着陆器的发展趋势进行了研究，指出具有全月面到达能力和障碍自检测能力是新一代着陆器的发展趋势；文献[8]对载人月球基地工程所必须解决的问题进行了论述，指出可移动着陆器对解决着陆点与月球基地之间运输任务有着重要的作用；以上研究均以概念设想为主，指出了可移动着陆器对未来月球基地建设、大型载荷装运和月面任务执行具有诸多优势，但未对具体结构和功能实现作出相关阐述。文献[9]提出了一种基于轮腿式的六足串联式可移动载人月面着陆器，该着陆器通过轮式的高速移动和腿式的高效避障实现星表移动，但串联式腿足构型无法承受较大的着陆冲击，且轮式腿足末端易发生侧滑。文献[10]提出了一种新型腿式移动着陆器，该着陆器腿足采用桁架—机构转换方法设计，可以在承受更大冲击载荷的情况下满足机构运动要求，实现软着陆和行走功能；文献[11]提出了一种可重构腿式移动着陆器，该着陆器集着陆与行走模式于一体，通过多模态协同优化策略对着陆器的构型进行了拓扑优化；文献[12]提出了一种基于桁架机构变换的腿式着陆器，该着陆器通过桁架—机构转换方法，对着陆器多参数进行优化，得到了最佳的着陆腿和着陆器尺寸；以上研究对可移动着陆器的构型进行了设计优化，在满足缓冲要求的情况下提高了机构的运动性能，但未设计机构运动轨迹及着陆器行走步态。文献[13-14]提出了一种可移动着陆器方案，二者均采取在原有着陆器主辅缓冲支柱上增加驱动的方式，实现腿足机构在星表的移动；文献[15]提出了一种用于着陆探测的并联式四足机器人构型，并基于机体调整量最小设计了该机器人的行走步态，验证了该机器人的运动灵活性，但四足着陆器行走控制复杂，需要实时调整姿态。

综上，设计一种兼具着陆缓冲、姿态调整以及稳定行走功能的着陆器，对实现非确知复杂星表环境下的稳定着陆、对物质出露丰富的崎岖地形区域的移动式深度探测、对人员和物资的转运以及星表基地建设等都具有重要的支撑作用。由于四足构型行走步态复杂，需进行实时调姿以保证着陆器不会发生倾覆，轮腿式着陆器无法承载巨大的冲击，越障行走中需要复杂的控制策略来保障其腿足稳定不发生侧滑[16]，故本文设计了一种缓冲/行走一体化腿足式六足着陆器，在完成其正、逆运动学建模和直行、转弯等步态规划的基础上，实现了缓冲机构足端期望轨迹向主动驱动关节伸缩量的映射，并通过虚拟样机仿真验证了运动学模型的正确性和运动步态的稳定性。

1 缓冲/行走一体化着陆器设计

1.1 着陆器构型设计

缓冲/行走一体化着陆器是一种兼具稳定着陆和灵活漫游两种功能的着陆器。本文设计的六足式缓冲/行走一体化着陆器由一个正六棱台式本体和六套按中心对称方式分布在本体周围的缓冲/驱动集成式三自由度腿足机构组成。着陆器本体用来安装各种科学载荷，着陆腿采用悬臂式构型，可在发射过程中通过变动辅助支柱的长度实现收拢，并在着陆前自行展开。图1为缓冲/行走一体化着陆器整机构型示意图。

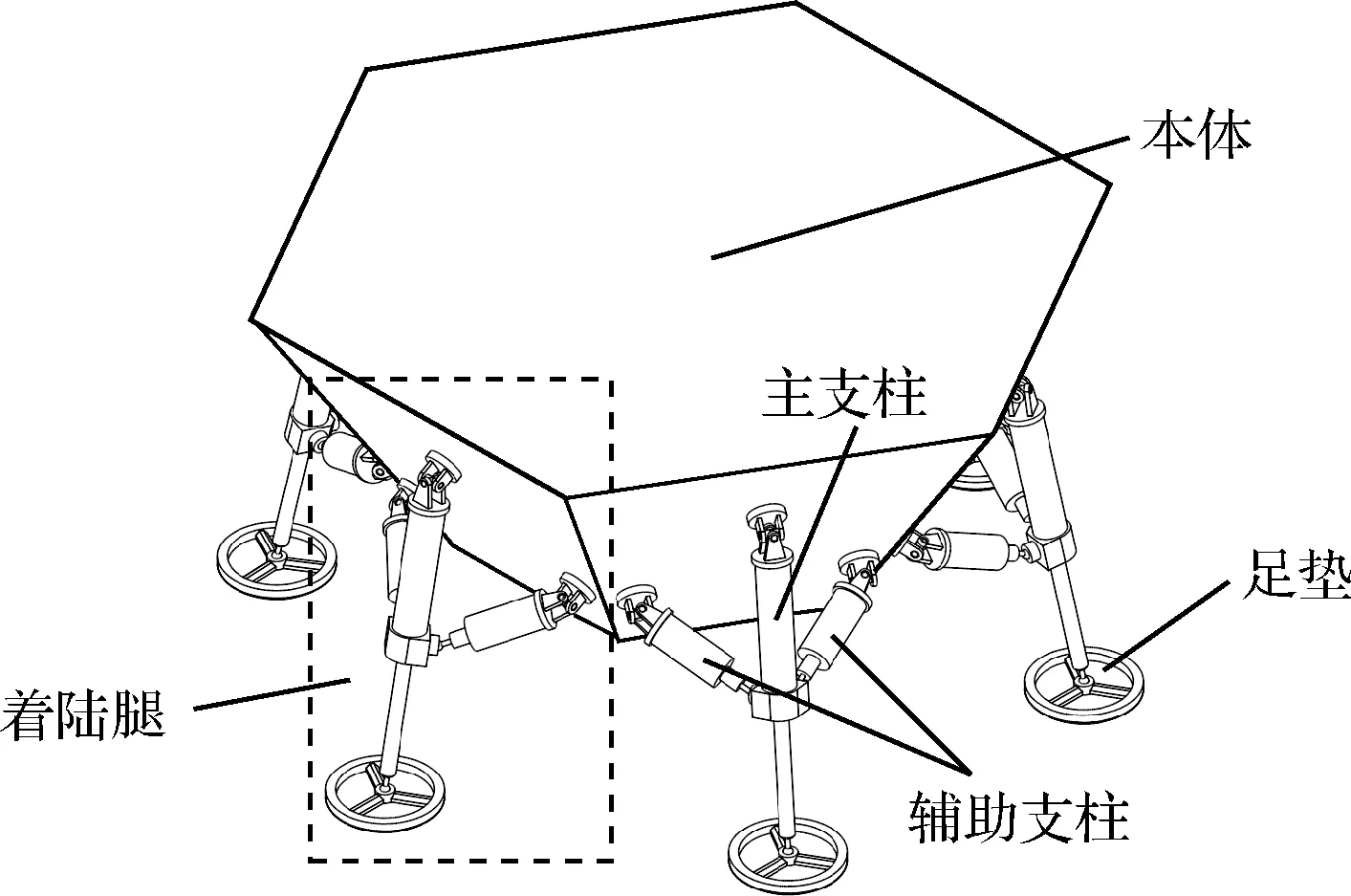
图1 缓冲/行走一体化着陆器Fig.1 Buffering/Walking integrated lander

1.2 缓冲/行走一体化功能实现

为实现着陆器的缓冲功能，每条着陆腿均由一个主支柱和两个辅助支柱构成。主辅支柱内置吸能/驱动集成式缓冲器，如图2所示。该缓冲器主要由活塞杆、内筒和外筒组成，内筒与外筒之间分别放置铝蜂窝缓冲材料，主支柱进行单向压溃缓冲吸能，辅助支柱可进行双向拉压缓冲吸能[17]。为实现着陆器的行走功能，每组主、辅支柱内均装有驱动装置。驱动装置由电机、减速器、制动器组成，配合滚珠丝杠可以实现主、辅支柱中活塞杆相对于内/外筒主体部分的伸缩运动。缓冲、行走功能的切换由缓冲/行走切换装置实现。当缓冲完成后，滑块与卡锁保持锁止状态，随后，驱动装置带动滚珠丝杠运动，实现活塞杆相对于内/外筒主体部分的伸缩，从而驱动着陆器行走。图2为吸能/驱动集成式缓冲器示意图。

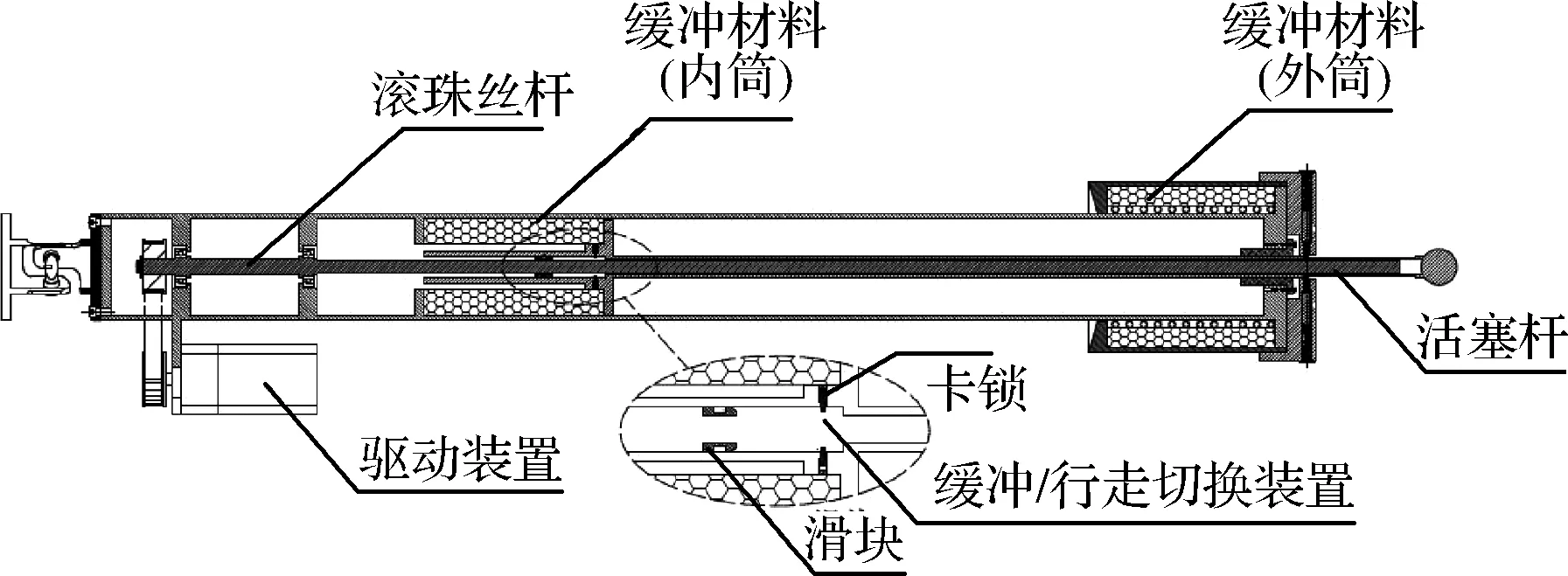
图2 吸能/驱动集成式缓冲器Fig.2 Energy-absorbing/driving integrated buffer

2 着陆器腿足机构运动学分析

为便于描述，建立单腿坐标系示意图，图3(a)为着陆器关键点位置示意图，图3(b)为各关节坐标系示意图。OB为着陆器本体质心，在该点处建立本体质心坐标系{OB}，O0为主缓冲支柱与本体连接点(A)，以该处胡克铰为转动关节建立坐标系{O1}、{O2}，O3为主缓冲支柱与足垫连接点(B)，以该点处球铰建立足端坐标系{O3}。

图3 着陆器单腿关节坐标系示意图Fig.3 Joint coordinates of lander single leg

2.1 单腿正运动学

如图3所示单腿机构坐标系定义，规定逆时针旋转为正。坐标系{O1},{O2}处的关节转角为θ1,θ2；{O3}处的伸缩位移为p1；L1为主支柱初始长度。根据连杆参数关系，由改进D-H参数法建立单腿机构连杆参数表[18-20]，如表1所示。

表1 着陆器单腿机构D-H参数表Table 1 Link parameters of single leg

(1)

(2)

(3)

(4)

可得单腿机构运动学正解，如式(5)所示。

(5)

式中：

(6)

2.2 单腿逆运动学

(7)

分离θ1项，可以得到

(8)

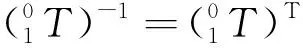
(9)

令方程两边的元素(1,4),(2,4),(3,4)相等，可得方程组

(10)

对方程组求解可得：

(11)

其中，关节转角θ2的转动范围由辅助支柱的伸缩位移限定，具体如表2所示，不会达到±π/2，故p1不会出现无解。

2.3 “UP-2UPS”映射

如图3所示单腿机构关节坐标系，U1和U2为辅助支柱与本体之间的胡克铰连接点，S1和S2为辅助支柱与主支柱之间的连接点。S1和S2在坐标系{O2}下的坐标分别为(x2,y2,z2)和(x3,y3,z3)，U1和U2在坐标系{O0}下的坐标分别为(x1,y1,z1)和(x4,y4,z4)。

由正运动学推导S1和S2的位姿矩阵，

(12)

(13)

将式(1)和式(2)与式(12)、式(13)分别相乘，可得：

(14)

(15)

由此可以得到S1和S2的位置矩阵分别为(px2,py2,pz2)T，(px3,py3,pz3)T，U1和U2的位置矩阵分别为(px1,py1,pz1)T、(px4,py4,pz4)T，其位置矩阵如式(16)和式(17)所示。

(16)

(17)

图3所示关节转角θ1和θ2发生转动后，根据U1,U2,S1,S2在坐标系{O0}内的位置坐标，可求得两组辅助支柱的伸缩变化量。至此，可以得到主、辅缓冲支柱的伸缩量与关节转角θ1,θ2之间的变换关系，如式(18)。

(18)

其中:L1为主支柱初始长度，L2和L3分别为辅助支柱初始长度。

最后，由上述推导对着陆器进行运动学求解，过程如下：

1)输入足垫末端的期望位姿矩阵，由逆运动学求解得到各关节角的转动量；

2)将各关节角转动量代入正运动学进行求解，得到主、辅支柱连接点处的位置变化量；

3)通过“UP-2UPS”映射方式，将主、辅支柱连接点处位置变化量作为输入，得到主、辅支柱中各直线驱动装置的伸缩位移量。

2.4 工作空间分析

着陆器构型参数及驱动装置伸缩边界如表2和表3所示。

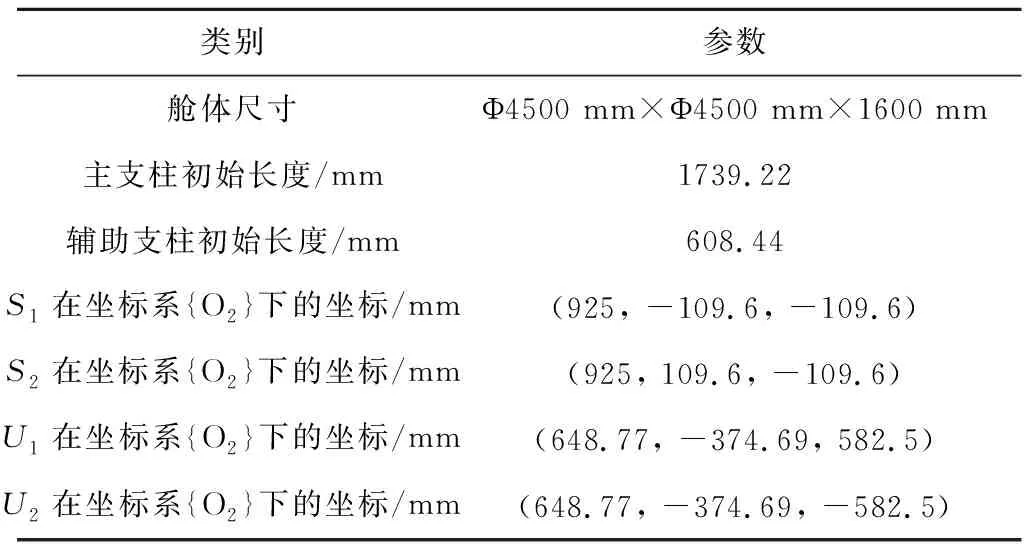
表2 着陆器构型参数表Table 2 Mechanism parameters of lander

表3 驱动装置伸缩边界Table 3 Moving boundary of driving device

根据以上参数，综合式(1)～式(18)，由蒙特卡洛法绘制该腿足式着陆机构的末端足垫相对于坐标系{O0}的工作空间[21]，如图4所示。

由图4(a)可知，足端工作空间在y轴方向对称分布；在z轴和x轴方向跨度较大，且分布合理。其中，x轴方向跨度为573～2092 mm，y轴方向跨度为-162～162 mm，z轴方向跨度为1123～2670 mm，结合着陆器主支柱初始长度，可知腿足机构可实现300 mm×300 mm的障碍物的跨越，如图4(b)所示。

3 着陆器步态规划

3.1 “3-3”步态

“3-3”步态是六足动物行走时速度最快且最稳定的一种步态，目前，六足机器人广泛采用“3-3”步态。其最大特点为任何时刻总有三条腿处于支撑相，且本体重心始终处于支撑三角形内。图5为“3-3”步态行走示意图，正六边形表示着陆器本体，其质心处于几何中心，6个圆点表示着陆器足垫末端位置，其中空心表示处于摆动相，实心表示处于支撑相[22]。

初始状态如图5(a)所示；当着陆器向前运动时，腿足2、4、6处于支撑并相对于本体向后摆动，使得本体质心向前移动，同时腿足1、3、5向上抬起，如图5(b)所示；之后腿足1、3、5放下处于支撑，此时如图5(c)所示；然后，腿足1、3、5处于支撑，腿足2、4、6向上抬起，如图5(d)所示；最后，腿足2、4、6向前摆动并放下，如图5(e)所示。至此，着陆器回到初始状态，完成向前运动的一个步态周期。

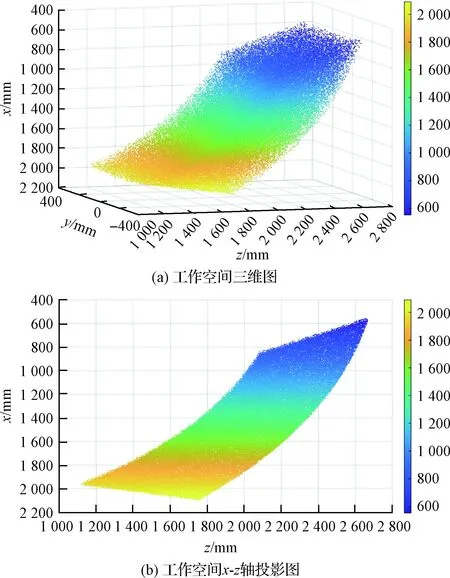
图4 足端工作空间示意图Fig.4 Leg-end workspace of lander

当着陆器需要转弯时，其初始状态如图6(b)所示。向左转弯时，腿足2、4、6抬起，腿足1、3、5相对于本体向左摆动，重复上述各阶段工作，着陆器即完成了左转，如图6(a)；向右转弯时，腿足1、3、5抬起，腿足2、4、6相对于本体向右摆动，重复各阶段工作，着陆器即完成了右转，如图6(c)。

3.2 足端轨迹规划

建立图7所示着陆器单腿机构迈步简图，其中O0为腿足1的根关节，OF为该腿足足垫末端位置点，OF′为足垫期望落足点。在着陆器向前运动过程中，假设其质心保持匀速运动，以足垫末端初始位置点为坐标原点在地面坐标系下进行足端轨迹规划。为方便描述，建立足端坐标系{OF}，坐标系{OF}下的zF轴、xF轴分别与坐标系{O0}下的y0轴、x0轴平行，足垫末端在迈步过程中坐标随时间变化用x(t)、y(t)、z(t)来表示。其中，单腿迈步步长为s，高度为h。

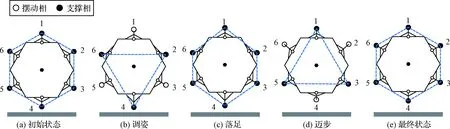
图5 “3-3”步态示意图Fig.5 “3-3” gait planning

图6 “3-3”步态转弯示意图Fig.6 “3-3” gait cornering planning

当单腿迈步步长为s，高度为h为0时，足垫末端位置在坐标系{O0}下随时间变化轨迹将为一直线，并且由于足垫与地面之间存在摩擦力，着陆器本体会相对于腿足机构的摆动方向而反向运动，即着陆器调整姿态。此时，由于足垫末端在坐标系{O0}下x0方向的值始终不变，因此将保证着陆器本体质心在xB方向不会发生较大起伏。

已知着陆器足端轨迹后，可根据逆运动学求解主、辅支柱内各直线驱动关节的目标伸缩量。由着陆器初始状态可得坐标系{OF}原点在坐标系{O0}下的坐标为(xF,yF,zF)，则足端轨迹在{O0}下可以表示为:

图7 着陆器单腿机构迈步简图Fig.7 Step track of lander

(19)

由式(11)可得关节转角和主支柱伸缩位移量分别为

(20)

之后，由式(18)可得主、辅支柱内各直线驱动关节的伸缩变化量。

4 仿真校验

仿真校验针对所提出的六足腿足式可移动着陆器开展，在ADAMS环境下完成了“3-3”步态仿真，如图8所示。着陆器初始状态如图8(a)所示，着陆器向右移动，腿足1、3、5抬起，腿足2、4、6处于支撑并相对于本体向后摆动，如图8(b)所示；之后，腿足1、3、5放下处于支撑，如图8(c)所示；然后，腿足2、4、6抬起，腿足1、3、5处于支撑，如图8(d)所示；最后腿足2、4、6向前摆动，后放下支撑，如图8(e)所示。至此，着陆器回到初始状态，完成向前运动的一个步态周期。

4.1 行走运动特性分析

着陆器行走过程中，本体质心位移如图9所示。图9(a)为着陆器本体质心前进方向时间—位移曲线，说明本体在沿前进方向(Z方向)按阶跃式节律进行移动，行走速度约为140 m/h；图9(b)为着陆器本体质心沿竖直方向的时间—位移曲线，呈周期波动，初始扰动为着陆器缓冲着陆过程，本体质心竖直方向(X方向)波动为12.59 mm(着陆器本体高度为1600 mm)，约占其本体高度的0.79%。着陆器行走过程中本体的俯仰角和横滚角变化如图10所示，横滚角维持在0°左右；由于着陆器本体相对于地面坐标系不断移动，俯仰角曲线随时间偏移，其中俯仰角最大值为0.62°，最小值为-0.19°，绝对值均值为0.314°。结果表明着陆器行走过程平稳可靠，未发生较大偏移。

图8 “3-3”步态仿真图Fig.8 Simulation of “3-3” gait planning

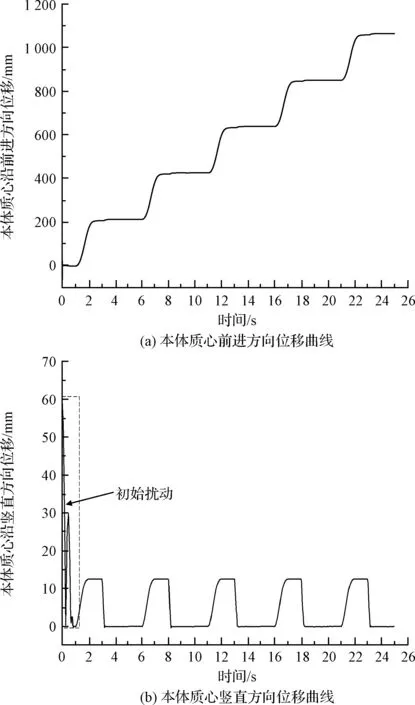
图9 着陆器本体质心位移图Fig.9 Body mass center displacement of lander

图10 着陆器行走姿态角变化曲线Fig.10 Posture angle of lander walking

着陆器行走过程中，腿足驱动装置位移曲线如图11所示。图11(a)为腿足机构2中各驱动装置时间—位移曲线，主支柱驱动行程为-3.2～5.4 mm，辅助支柱行程分别为-85.25～0 mm、-15.44～0 mm。图11(b)、(c)为腿足机构4、6中各驱动装置时间—位移曲线，各驱动装置位移一致，呈周期变化，主支柱行程为-13.65～56.88 mm，辅助支柱行程均为-43.90～0 mm。由于着陆器前进方向与腿足机构4内y0轴平行，因此腿足机构4中两组辅助支柱驱动行程相同，腿足机构2和腿足机构6内y0轴与前进方向存在夹角，因此腿足机构2和腿足机构6中的两组辅助支柱驱动行程不同。可以看出，驱动装置位移曲线平顺，满足主辅支柱伸缩边界要求。

图11 着陆器驱动装置位移图Fig.11 Device displacement of lander

4.2 行走稳定性分析

稳定裕度是衡量着陆器行走稳定性的一项关键指标。为准确评定着陆器的行走稳定性，规定稳定裕度为着陆器本体质心在水平面内投影点至支撑多边形各边距离的最小值。着陆器行走过程中，稳定裕度变化曲线如图12所示，着陆器初始状态下稳定裕度为1795 mm，行走过程中最大稳定裕度为1050 mm，最小稳定裕度为861 mm，平均稳定裕度为979.125 mm，平均稳定裕度值为初始稳定裕度值的54.55%，结果表明了着陆器行走过程中具有良好的行走稳定性。

5 结 论

本文提出了一种悬臂腿足式缓冲/行走一体化六足着陆器，在对该着陆器UP+2UPS悬臂式腿足机构进行了运动学分析的基础上，设计了“3-3”行走步态，规划了足端轨迹并进行了虚拟样机仿真。结果表明：UP+2UPS悬臂式腿足机构运动平顺稳定，驱动装置位移曲线平滑可靠；腿足机构可达空间满足行走步态要求且具备300 mm×300 mm障碍物跨越能力；“3-3”行走步态稳定，无较大起伏与偏移，本体起伏占其高度的0.79%，横滚角维持0°左右，俯仰角均值为0.36°，稳定裕度高，平均稳定裕度为979.125 mm。本文研究成果为该类型着陆器的研制提供了一定的理论基础，可作为缓冲/行走一体化星表着陆器的设计参考。