机器人在轨构建空间桁架结构的装配序列规划方法

罗建军，王嘉文，王明明，刘 聪

(1. 西北工业大学深圳研究院，深圳 518057；2. 西北工业大学航天学院航天飞行动力学技术重点实验室，西安 710072)

0 引 言

随着航天技术的进步与应用需求的拓展，代表国家科技实力的空间站、空间反射镜、通信天线、太阳能电站、地外基地等空间大型平台和基础设施的建设需求日益迫切。空间在轨服务可以拓展人类的太空活动，帮助人类进行更广泛、更深入、更创新的空间探索活动[1]。而一些体积或质量较大的空间设施无法通过运载火箭一次部署完成，需多次发射在空间中进行组装构建。空间在轨装配是指在太空中，将不同的部件连接起来，构建成为一个由结构、子系统或子系统的单元体等组成的空间设施。在轨装配扩大了我们设计任务的空间，增加了人类太空活动的多样性[2-3]。空间在轨装配技术未来的发展方向是空间自主装配，而智能装配序列规划是实现装配智能化、自主化、自动化的关键问题。智能装配序列规划的意义在于检测出可行的装配序列，在考虑各种装配过程约束的情况下，寻找最优的装配序列。根据装配序列，对装配过程的各个方面进行更优的设计和安排。另外，合理的装配顺序有利于提高装配效率，降低装配成本。装配序列的自动生成和优化对于整个任务的进行至关重要[4]。

从20世纪70年代开始，NASA兰利研究中心就进行了一系列的研究[5]。1980年，该中心在地面零重力模拟池中进行了手动装配四面体的实验[6]。1985年11月，在“亚特兰蒂斯”号航天飞机上，两名航天员手动装配一个13.7 m的桁架结构，以此评价手动装配的有效性[7]。随着机器人技术与空间机械臂的发展，自主装配成为空间装配更好的解决方式，也是未来发展的趋势[8-14]。

针对空间结构的在轨装配序列规划方法，目前已有一些研究工作。可以按照是否考虑机器人的运动，将装配序列规划分为两类。对于不考虑机器人运动装配的问题，通常利用图论的方法建立可行解，采用软计算的方法求最优序列。其中，Bonneville等[15]使用了遗传算法进行求解。Chen等[16]对遗传算法进行了改进，加入交叉变异操作以解决算法陷入局部最优的问题。Lazzerini等[17]使用了分段编码的遗传算法，提高了求解速度。Hong等[18]提出了一种具有启发式工作规则的三阶段集成方法，以帮助计划器生成最佳和最有效的装配序列，最后使用反向神经网络方法进行求解。Cao等[19]研究了一种新的免疫算法在装配序列中的应用。并将两种人工免疫算法模型(骨髓模型与否定选择算法)相结合，缩短了计算时间。Motavalli等[20]使用模拟退火算法给出了用于序列优化的评价函数。Wang等[21]利用离散粒子群算法对装配序列进行求解。Bahubalendruni等[22]则考虑装配过程中的机器人避撞与能量消耗，用粒子群算法求解最优装配序列。曾冰等[23]提出利用萤火虫算法进行序列规划。Li等[24]对萤火虫算法进行了改进，赋予萤火虫可变视距的能力，提升了萤火虫算法的性能。Failli和Dini[25]首先使用蚂蚁系统进行序列检测和优化，Wang等[26]提出了一种新的蚁群算法来生成和优化产品的装配序列。郭继峰等[27]将桁架系统进行分层规划，并用蚁群算法求解。梁丽芬等[28]结合基于模型定义技术，采用混沌粒子群算法对装配序列进行求解。

利用机器人进行装配的序列规划问题与传统的序列规划不同，需要考虑机器人对整个装配过程的影响。文献[25]考虑了机器人的可抓捕性与装配方向，并对可装配性进行定义，完成了考虑机器人的装配单元装配序列规划。文献[29]对多机器人装配问题进行分析，将其转化为约束满足问题。通过对可行的重抓取进行假设，将约束满足问题进行解耦，分解为独立的小问题，使求解速度大幅度提高。文献[25, 29]只考虑了机器人对装配过程的影响，并没有对各机器人的规划与控制进行具体设计与求解，而本文具体分析了机器人的运动，并设计了关节轨迹与控制器。文献[30]将机器人装配序列规划问题分为两层，逻辑层与物理层。在逻辑层中规划序列，并通过物理层进行检测并反馈，对逻辑层规划结果进行改进。引入了反馈机制，提高机器人装配序列规划效率，但是没有考虑机器人在整个装配过程中的控制问题。文献[31]分析了利用机器人构建张拉结构的序列规划问题，利用基于采样的运动规划方法。文献[32]对机器人增材制造三维桁架的自动序列和运动规划问题进行了研究，并提出了一个新的层级式规划框架，以解决通常规划时间长、配置复杂的挤出式序列和运动规划问题。文献[31-32]中没有考虑机器人的装配操作，只对机器人的末端轨迹进行了规划。本文考虑装配运动的特殊性，对机器人装配动作进行了特殊设计，引入力反馈设计，增加了装配的可靠性。文献[33]针对装配过程中机器人在桁架上的攀爬移动问题，对机器人的移动步态进行了分析。文献[34]提出一种基于强化学习的自适应方式，在四旋翼无人机装配桁架结构的背景下，求解了桁架装配顺序与无人机装配时的路径规划问题。

本文针对采用机器人在轨构建空间桁架结构的装配序列规划问题，设计了机器人装配系统，并围绕此系统，提出了一种可同时求解机器人运动规划与控制的序列规划方法。在装配系统设计方面，本文采用仿生设计方法，设计了具有双末端执行器的装配机器人；在机器人运动规划与控制方面，本文设计了机器人的攀爬运动规划与轨迹跟踪控制方法以及装配运动规划与力控制方法；在序列规划寻优方面，本文建立了考虑机器人运动路径与控制能耗的评价指标，并采用离散粒子群算法对其进行求解。在仿真方面，本文构建了采用所设计机器人进行空间桁架装配的任务场景，求解得到装配序列与机器人运动与控制，校验了本文方法的有效性与先进性。

区别于之前的序列规划方法，本文的方法具有如下三方面优势：首先，分析了机器人在装配过程中的运动与控制方法。第二，在传统序列规划求解装配单元装配序列的基础上，还可以得到机器人运动等信息。第三，建立了考虑机器人的运动路径与燃料消耗的装配序列评价函数，保证机器人运动路径最短，能耗最低。

1 在轨装配系统设计与建模

1.1 装配系统设计

本文基于仿生学理念，参考蛇的构型以及猴子等攀爬类动物的动作，设计了灵活、自由的装配机器人。该机器人具有两个末端执行器，皆可抓持在空间桁架结构上。抓持在空间桁架结构上的末端执行器即可视为基座。在进行移动操作时，可通过改变机器人构型，同时两个末端执行器轮流抓持空间桁架结构，完成机器人在空间桁架结构上的移动。在进行装配操作时，可使机器人一端抓持住空间桁架结构充当基座，另一端完成装配操作。

装配机器人可根据任务要求设置自由度，一般采用六自由度或以上(见图1)，以增加机器人的灵活性。机器人采用模块化的设计思想，各个关节由彼此独立的模块连接而成，可以根据不同的任务需求改变机器人的自由度以及构型配置，也可以通过改变执行器结构以完成不同的任务。

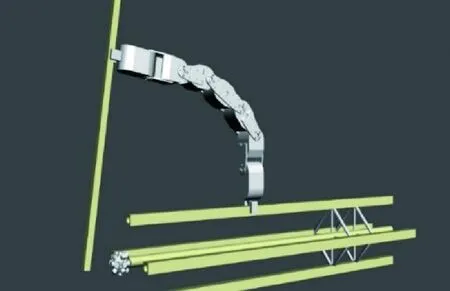
图1 机器人装配空间桁架结构示意图Fig.1 Illustration of robot assembly space structure

1.2 装配机器人建模

(1)

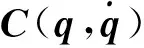
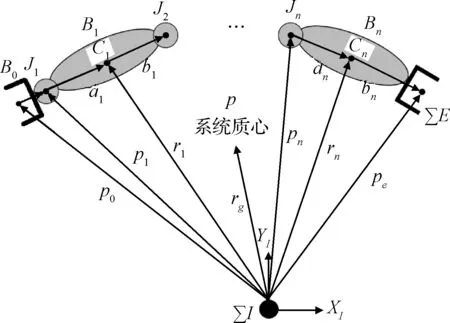
图2 装配机器人的一般模型Fig.2 General model of assembly robot

(2)

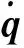
(3)

式中：δt为求解步长。当装配机器人末端执行器切换充当基座时，机器人的广义坐标与D-H参数发生变化，需要重新进行建模。为求解方便，装配机器人一般采用对称设计，在末端执行器切换时，只需将对称关节角进行交换定义即可。

2 装配机器人运动分析

本文根据控制策略的不同，将机器人运动分为巡游运动与装配运动两类。巡游运动完成机器人在空间桁架结构上的移动，装配运动完成各装配单元间的装配。

2.1 巡游运动

由于机器人运行在空间环境，因此，设计装配机器人的运动步态时，需确保可靠性。

当装配机器人在同一根杆上需要向前移动时，本文设计了滑行运动步态(见图3)。在受到干扰时，两个末端执行器夹爪皆可迅速抓紧杆件，保证装配机器人的安全。滑行运动步态具体运动步骤如下：

1)机器人位于初始位置，由夹爪1支撑整个机器人，夹爪2逐渐松开。

2)机器人开始收缩中间关节，使夹爪2沿着杆件滑行移动到预定位置。

3)夹爪2逐渐夹紧，夹爪1松开，完成机器人基座转换。重复此动作完成机器人的移动。

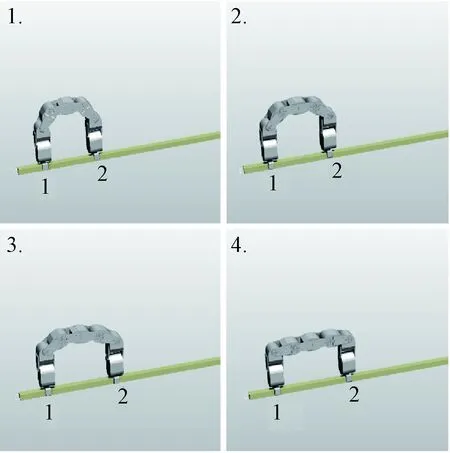
图3 滑行运动步态Fig.3 Sliding gait

图4 翻转运动步态Fig.4 Turnover gait

当装配机器人需要在两根杆间完成跨越时，要求装配机器人步态较大，本文在此设计了翻转运动步态(见图4)。翻转运动步态具体运动步骤如下：

1)机器人位于初始位置，由夹爪1支撑整个机器人，夹爪2逐渐松开。

2)机器人中间关节开始运动，夹爪2慢慢远离杆件，使机器人完成整体翻转。

3)夹爪2运动到预定位置，夹爪1松开，完成机器人基座转换；重复此动作完成机器人的移动。

在设计机器人关节轨迹后，采用逆动力学控制对所设计轨迹进行跟踪，关节控制律为：

(4)

式中：ν为辅助控制输入。

(5)

求得误差动力学为：

(6)

选取合适的增益矩阵KVT与KPT即可保证控制系统稳定。

2.2 装配运动

当装配机器人需要执行装配操作时，首先从初始状态运动到装配准备状态，随后夹持装配单元杆件，开始进行装配运动(见图5)。具体步骤如下：

1)机器人位于初始位置，由夹爪1支撑整个机器人，夹爪2逐渐松开。

2)机器人中间关节开始运动，夹爪2慢慢远离杆件，机器人整体翻转，直到夹爪2运动到预定位置，机器人进入装配准备状态。

3)夹爪2夹紧装配单元杆件，完成装配运动。

图5 装配机器人装配运动示意图Fig.5 Illustration of assembly movement of assembly robot

机器人从初始状态运行至装配准备状态时，依然采用第2.1节的规划与控制方法。在装配开始后，首先完成机器人末端执行器z轴方向上的力控制，然后再保持接触力，完成x-y平面上的遍历搜索。具体流程如图6所示。

图6 装配运动流程图Fig.6 Assembly motion flow chart

在建模时，本文忽略机器人的柔性，将机器人建模为刚体，将机器人接触的环境，也就是桁架结构的杆件，建模为柔性体，其刚度用KP表示。当机器人末端与环境接触产生微小位移δx时，所产生的弹性恢复力为：

F=-Kpδx

(7)

(8)

设计机器人在末端执行器z轴方向上的柔顺控制律为：

(9)

本文力位混合控制器采用R-C控制器，R-C控制器不考虑力控制与位置控制动态耦合的影响。因此，机器人装配过程中两个阶段的控制力为：

(10)

3 装配序列规划

传统装配序列规划只对装配单元进行建模，求解各装配单元的装配顺序。而针对采用机器人进行装配的序列规划问题，还应考虑机器人的规划与控制。将传统的装配序列规划问题(ASP)转变成任务与运动规划问题(TAMP)。

3.1 装配过程建模

与传统的装配序列规划相同，首先衡量装配单元之间的关系。根据装配桁架结构，计算装配关系矩阵[36]。在本文中，装配关系矩阵包括干涉矩阵、连接矩阵和支撑矩阵三种。

除此之外，本文所规划的装配序列考虑了机器人对装配的影响，其中包括装配过程中的机器人运动路径最短，能耗最小，因此建立机器人装配的运动模型。本文基于图论理论将机器人运动环境建模为无向图，随后采用A*算法求解装配路径。因此本文假设机器人消耗的能量只有关节驱动部分。根据第2节求出的机器人关节控制力矩，建立机器人绝对值形式的能量消耗评价函数：

(11)

3.2 评价函数

本文针对机器人装配空间桁架结构的特点，采用四个评价指标：装配可行性，装配稳定性，装配路径与装配能耗。前两个指标描述装配单元的装配情况，文献[37]已经叙述了其计算方法。后两个指标描述装配过程中机器人的情况，计算方法如下：

1)装配路径

装配路径表示在装配过程中，各机器人所运动的路径长度之和。建模为无向图G=(V,E)，并计算SR(Σ)=[SR(Σ),SR0(Σ)]，nl=nl+nl0。所有装配单元检测完成后，输出各机器人路径SR(Σ)与机器人运动路径之和nl。显然，nl越小，机器人行驶总路径越短，装配越优。

2)装配能耗

装配能耗表示在装配过程中，各机器人消耗能量之和，将其定义为ne。对于装配序列{P1,P2,…,Pn}，在计算完机器人路径SR(Σ)后，根据4.4能耗计算方法，求解机器人能耗F，令ne=F，并输出各机器人运动规划qd与控制律τ。显然，ne越小，机器人消耗总能量越小，对装配有利。

将以上评价指标进行归一处理，建立函数模型，准确评价装配序列的优劣。对于序列{P1,P2,…,Pn}，其评价函数为：

(12)

装配评价指标中，(1)、(2)两个指标为约束指标，不满足该指标的装配序列无法完成装配。因此，满足装配序列可行的约束条件为：

(13)

其中，nc代表装配稳定性，ns代表装配支撑性，nl代表装配路径，ne代表装配能耗。ω1,ω2,ω3,ω4分别代表各指标权重系数，且ω1+ω2+ω3+ω4=1。各权重系数可根据不同装配的不同需求制定。而约束条件代表装配序列满足的前提条件，即在装配每一步都需要是稳定的且每一步都有可进行装配的方向，即与之前的装配不发生干涉。

3.3 离散粒子群

空间桁架在轨装配序列规划是一个离散整数组合优化问题。在此采用离散粒子群算法求解。在装配序列规划中，装配序列为待优化项。因此，用粒子i的位置表示装配序列，粒子i的维数即为装配单元个数。粒子i的位置表示如下：

Xi=(xi1,xi2,…,xin)

(14)

其中，xij为从1～n互斥的整数,n为粒子i的维数，即装配单元个数。xij表示粒子i的j维分量，代表装配序列Xi的第j个装配单元。初始装配序列可以随机生成，也可以人为辅助给出。粒子的速度决定粒子位置的改变，与粒子位置维数相同。因粒子中所有元素互不相同，因此粒子速度可看成对粒子位置中元素位置的调整。粒子i的速度表示为：

在多方共赢的工学结合培养模式下，本专业教学水平全方面提升，教师专业技能得到锻炼，近年来连续获得省级技能竞赛二等奖，行业竞赛一等奖等教学成果；课程内容进一步完善，不断产生教学改革、课程改革等项目；学生就业率与对口率逐渐提高。学院在合作过程中大量减少校外实习基地建设精力与经费，同时节约教师专业技能培训开支。通过技术工作室外包服务孵化学生创业，产生校园创业项目，与企业合作范围不断扩大过程中提高学院在行业中的知名度，提高相关专业就业情况。

Vi=(vi1,vi1,…,vin)

(15)

其中,vin表示粒子i第n个装配单元的速度，初始粒子速度随机生成。

由于装配序列具有的特殊性质，需要对粒子速度与位置作出约束，粒子位置中的元素应包含所有装配单元编号且不能重复。因此对粒子与运算准则进行重新定义[38]，采用下式对粒子i的速度与位置进行更新：

(16)

式中:w为参数惯性权重，其控制前一代速度Vi(t)对此时速度Vi(t+1)的影响；c1与c2为学习因子，c1控制个体历史最优位置Pi(t)对速度Vi(t+1)的影响；c2控制全局最优位置Pg(t)对当前速度Vi(t+1)的影响。

4 仿真校验

为了证实所提出的在轨装配序列规划的方法，本文以7自由度机器人装配常用空间桁架结构为仿真场景，在第4.1节中对机器人、桁架及仿真需要的各项参数进行定义；在第4.2节中分析并验证了装配过程中的机器人运动以及控制器设计的有效性；在第4.3节中验证了该桁架结构的装配序列，并最终给出机器人在整个装配任务中的运动规划与控制。

4.1 仿真场景

本文以文献[39]中所述空间桁架基础结构为例设计仿真场景，图7所示，该结构在空间可进行平铺与扩展，是空间众多设施构建的基础结构。因单个杆件安装复杂度较高，本文将基础结构分解成三个四面体与六根单杆，一共九个装配单元进行研究，以减少装配操作，提高装配效率与可靠性。且四面体设计为可折叠结构，采用折叠与装配共同构建大型空间桁架的方法，综合各方面的优点，既可减少装配单元数量与装配操作，也可以构建大型结构。

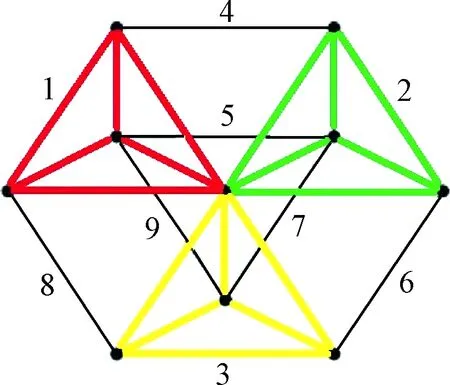
图7 空间桁架基础结构示意图Fig.7 Illustration of space truss foundation structure

机器人采用7自由度，具有两个末端执行器，机器人具体动力学参数如表1所示。

4.2 机器人运动仿真分析

机器人在整个装配中的运动分为两部分:同一根杆上的移动与两根杆之间的跨越。根据第2.1节规划的滑行运动步态，机器人规划初始关节角q0=[0,π/3,0,π/3,0,π/3,0]，切换末端执行器时规划目标关节角为qt_s=[0,π/8,0,3π/4,0,π/8,0]，本文采用三次多项式插值法规划关节轨迹。在控制器设计中，为验证控制器性能，给出机器人关节角初始误差eq0=[0.02，0.1，-0.01,-0.1,0.01,-0.1,-0.02]，控制律中KPT=250E，KVT=10E，E为单位矩阵。机器人完成该动作后，末端执行器切换充当基座，需要重新对关节角进行编号，此时机器人目标关节角变为初始关节角，控制机器人回到初始状态。至此，机器人滑行运动一次步态完成。

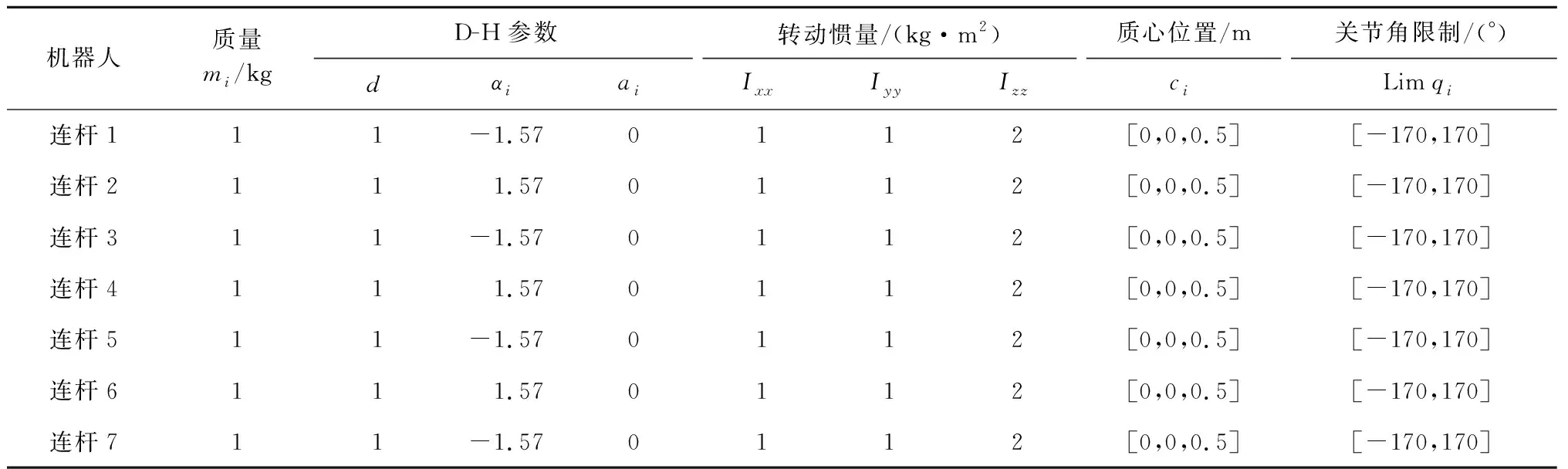
表1 装配机器人的运动学与动力学参数Table 1 Kinematic and dynamic parameters of assembly robot

图8 滑行运动步态机器人关节角变化Fig.8 Joint angle of robot’s sliding gait

针对本文仿真场景，可将异杆跨越运动分为60°异杆跨越运动步态与90°异杆跨越运动步态。60°跨越运动中，切换末端执行器时的目标关节角为qt_60=[0,-π/9,0,-π/9,0,-π/9,0]，90°跨越运动中为qt_90=[0,-π/6,0,-π/6,0,-π/6,0]。关节角初始误差为eq0，控制律中KPT和KVT与同杆运动相同。完成该动作后回到初始状态，异杆跨越步态完成。

图9展示了60°异杆跨越运动步态下的关节角变化。从图9可以看出,规划关节角变化平滑，控制器性能优越，跟踪误差较小。图10展示了90°异杆跨越运动步态下的关节角变化，仿真结果与60°异杆跨越运动步态相近，效果良好。

第一阶段仿真控制机器人末端与装配单元期望接触力为[0,0,-2]，桁架杆件刚度为300 N/m。机器人初始末端相对基座位置为[3,1,1.6]，相对基座姿态为[0,0,-π/2]；实际装配时机器人末端相对基座位置为[3,1,1]，力控制律设计中KP=4E，KE=8E。图11与图12所示为z轴方向接触深度与接触力变化图。从图11～12可以看出，接触深度最终稳定在0.007 mm，接触力稳定在2 N，完成了装配接触力控制的目标。

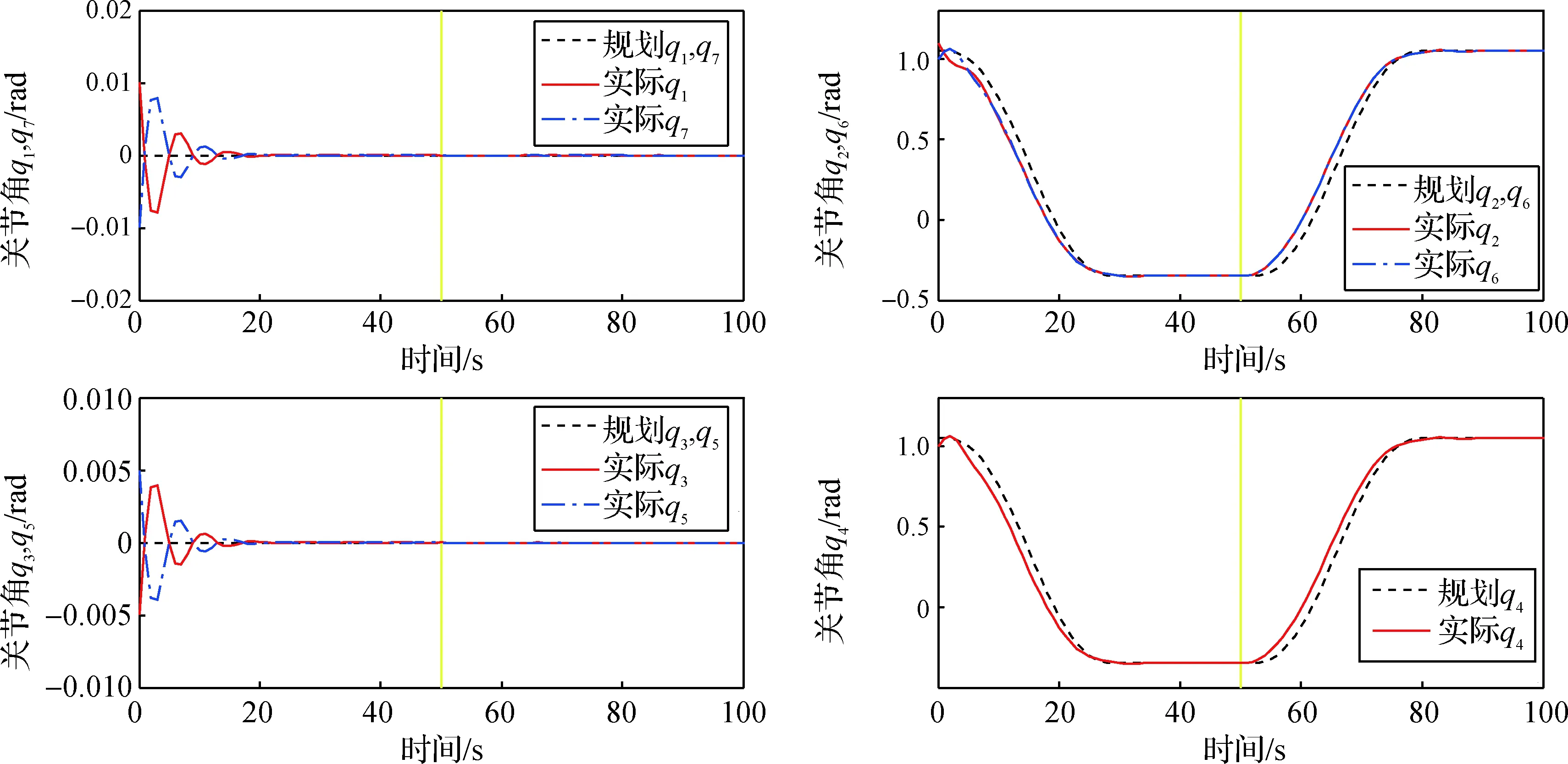
图9 60°异杆跨越步态机器人关节角变化Fig.9 Joint angle of robot’s 60° stride over gait

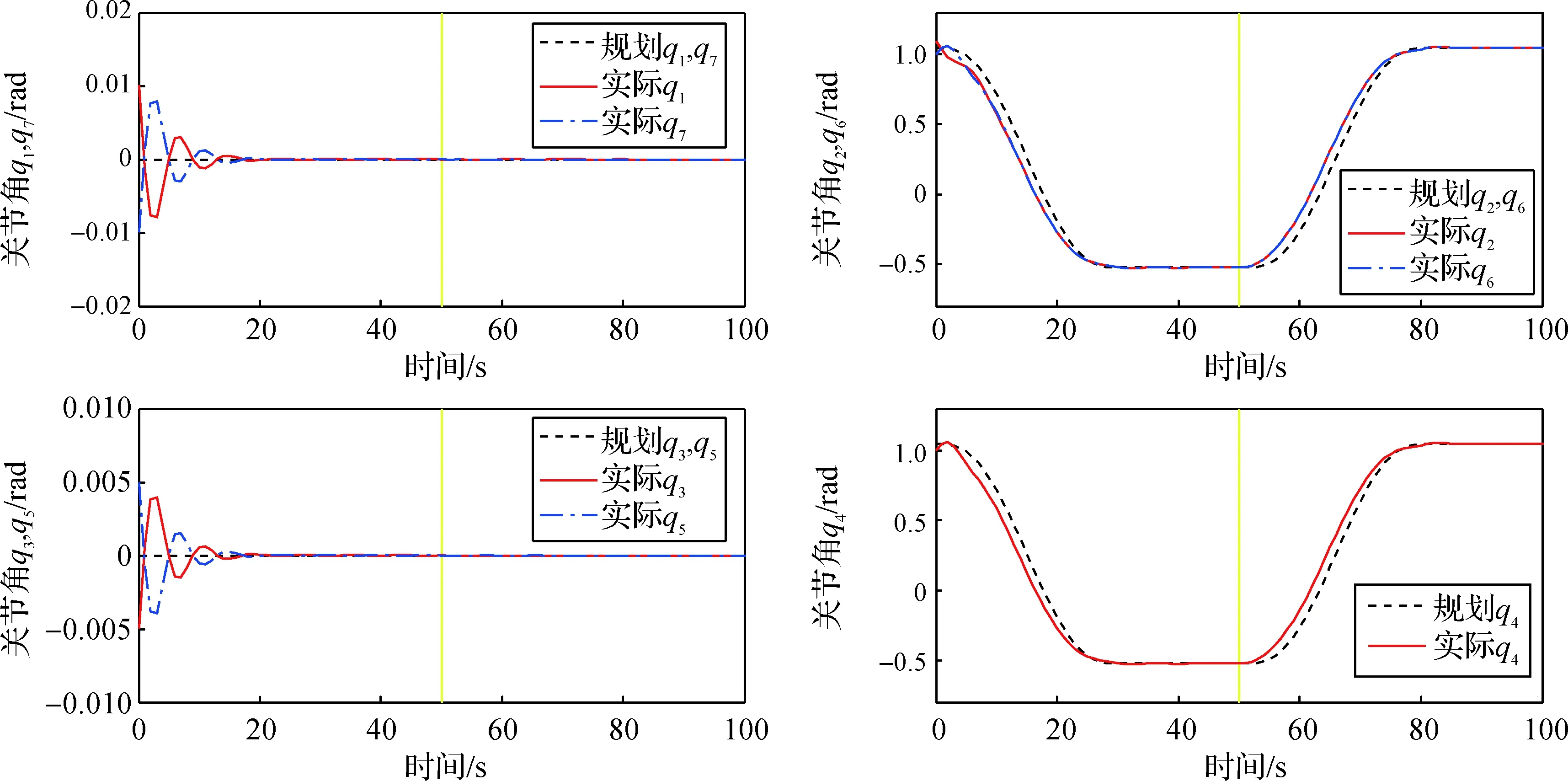
图10 90°异杆跨越步态机器人关节角变化Fig.10 Joint angle of robot’s 90° stride over gait

图11 z轴接触深度Fig.11 Contact depth of z-axis

图12 z轴接触力Fig.12 Contact force of z-axis

图13展示了装配第一阶段下的关节控制力矩变化。从图13可以看出，关节控制力矩最终趋于稳定，但是不都为零，这是因为此部分关节力矩用来保持接触力稳定。

图13 装配第一阶段机器人关节控制力矩变化Fig.13 Joint control torque of assembly first stage

第一阶段仿真控制机器人在z轴保持接触力的同时，在x-y平面进行螺旋遍历搜索。跟踪控制律设计中KPT=300E，KET=20E。图14所示为机器人末端轨迹图。从图14可以看出，所设计控制律跟踪效果优秀，允许装配范围覆盖末端轨迹经过的所有区域，在装配出现误差且无视觉辅助情况下，可消除误差，成功装配。

图14 装配第二阶段机器人末端位置变化Fig.14 End-effector position of assembly second stage

4.3 装配序列规划

本仿真中假设装配单元之间皆为稳定连接。在桁架标注抓取点并建立无向图如图15所示。

图15 抓取点编号及无向图建模Fig.15 Grab point number and modelling graph model

本文中装配能耗采用绝对值形式进行计算，图16展示了一次巡游运动与装配运动下的机器人能耗变化图。

图16 巡游运动与装配运动能耗变化Fig.16 Energy consumption of patrol and assembly movement

本文仿真在求解时，假设：1)装配环境不存在重力，且各装配单元之间连接都为稳定连接；2)机器人在运动过程中无外界干扰，在装配过程中无误差；3)不考虑机器人运输与拾取装配单元的操作；4)编号为1，2，3的四面体装配单元，在每条边上机器人只需要一步即可跨越至相邻杆。而编号4，5，6，7，8，9的六个单杆装配单元，机器人需要做一步同杆移动的动作，方可跨越至相邻杆。

基于上述假设，评价函数式(12)中ω1=ω2=0，考虑机器人路径与能耗对装配过程的影响，在此设置ω3=0.3，ω4=0.7。种群数量为20，进化次数为500。学习因子c1=0.2，c2=0.8。取w=0.4,0.7,0.9时，得到适应度函数变化曲线，如图17所示。

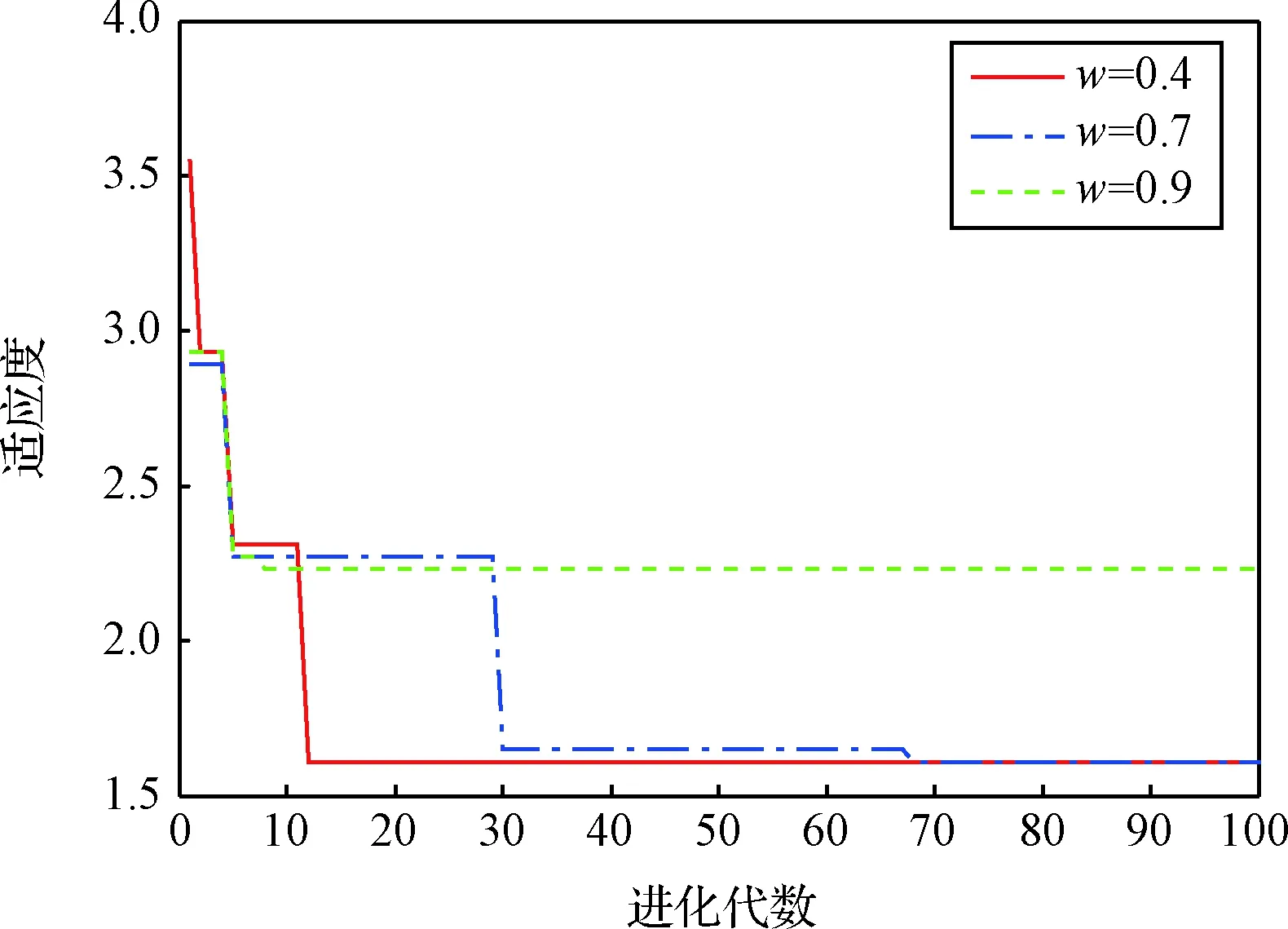
图17 参数惯性权重w对适应度的影响Fig.17 The influence of parameter inertial weight w on fitness function

从图17可以看出，最终适应度函数fmin=1.6111，与其对应的最优序列、机器人运动路径、机器人动作等装配规划如表2所示。

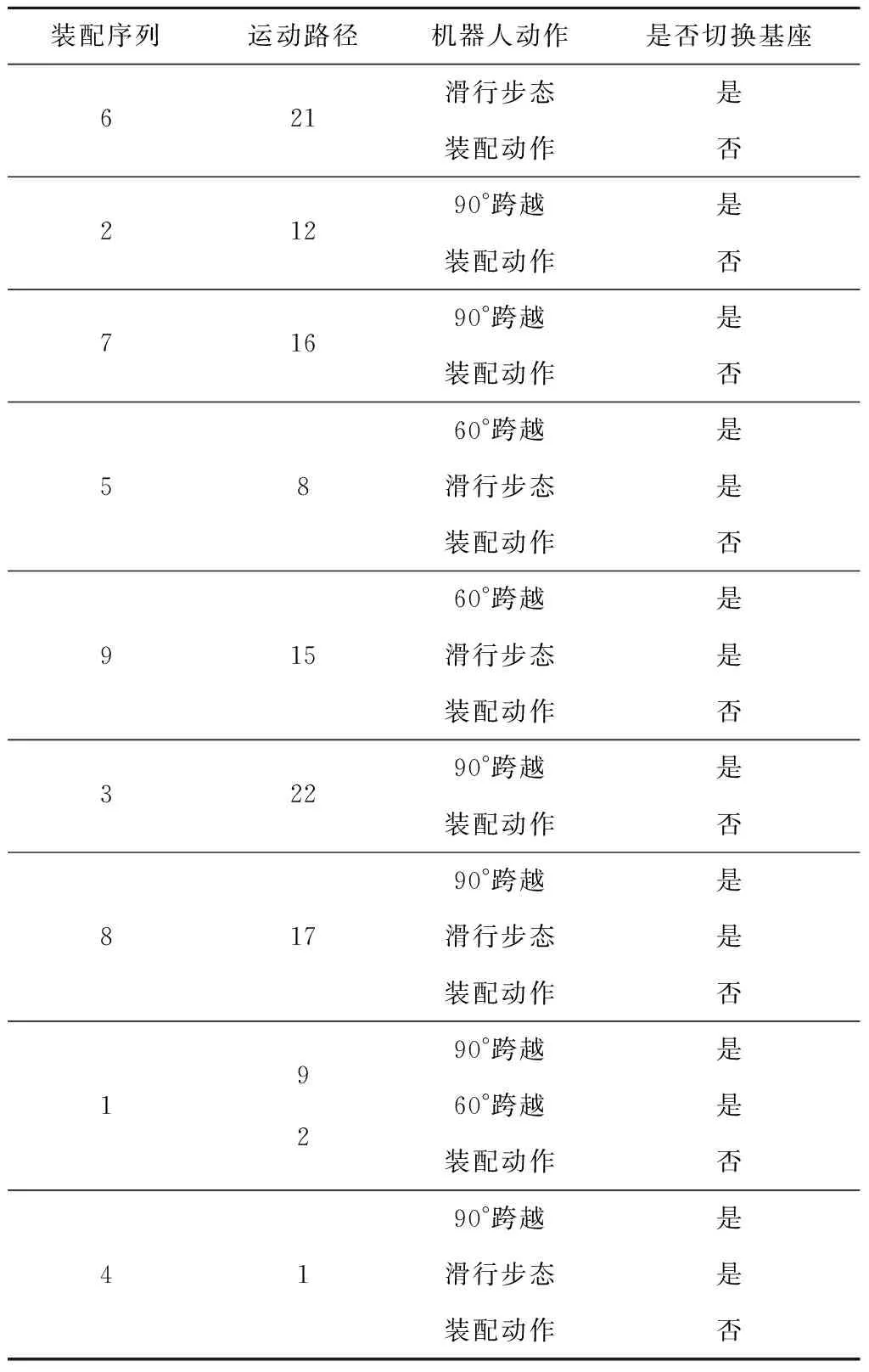
表2 机器人装配桁架的序列规划Table 2 Sequence planning of robot assembly truss

图18展示了机器人在整个过程中的运动路径变化，与表2中的机器人运动路径一一对应。

图18 装配中的机器人运动路径规划图Fig.18 Robot motion path planning in the assembly process

图19～图21展示了整个装配过程中的关节角、关节控制力矩以及能耗变化。横坐标的一个刻度代表机器人的一个动作，与表2中规划机器人动作一一对应。点划竖线代表末端执行器切换时刻，与表2中是否需要切换末端执行器一一对应。图19～21可看出机器人关节角运动曲线平滑，所设计控制律跟踪误差小，每个阶段机器人运动后都回到初始状态。关节控制力矩可用来指导各关节舵机的选择。机器人能耗可用来指导机器人能量储备规划。

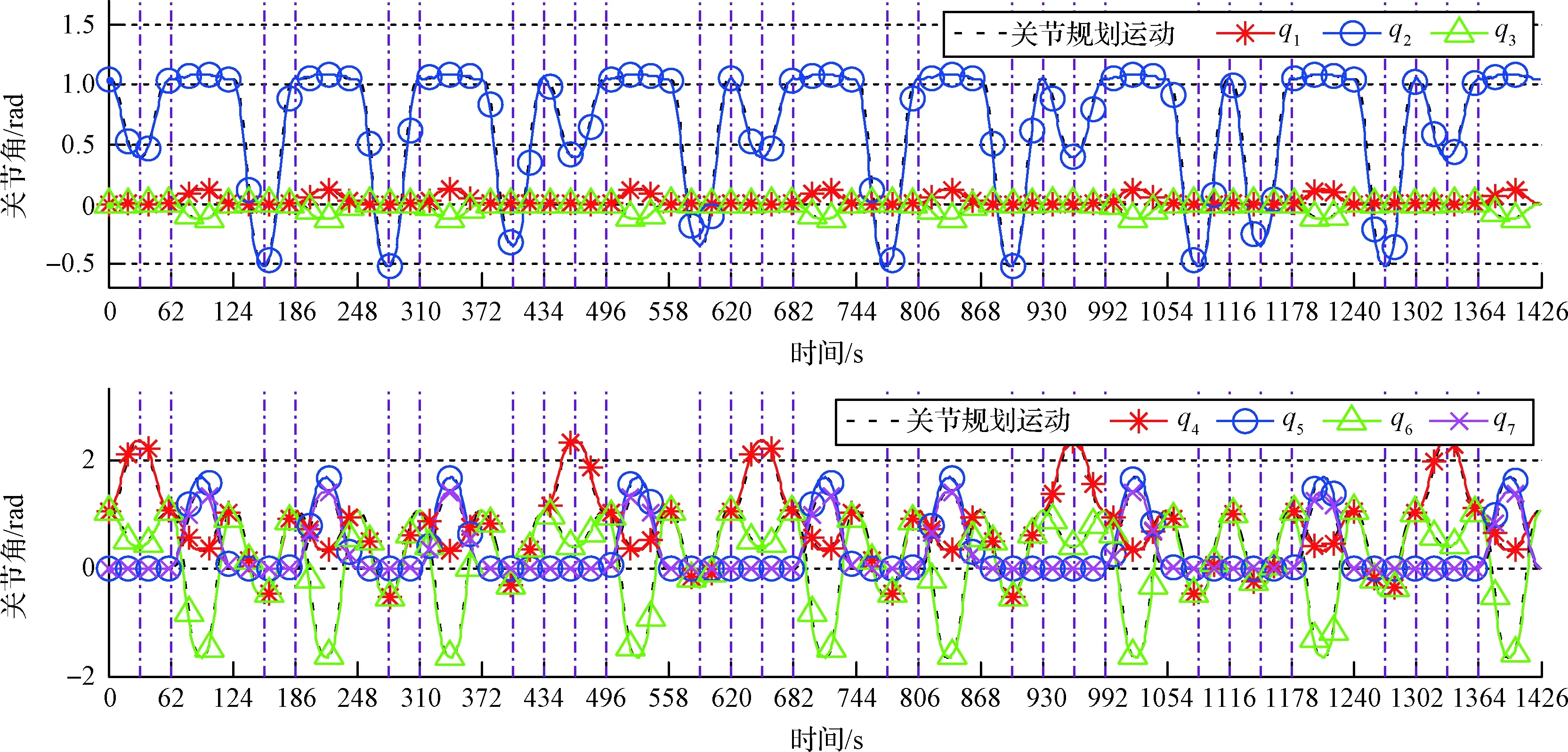
图19 整个装配过中的机器人关节角变化图Fig.19 Joint angle in the whole assembly process

图20 整个装配过中的机器人关节控制力矩变化图Fig.20 Joint control torque in the whole assembly process

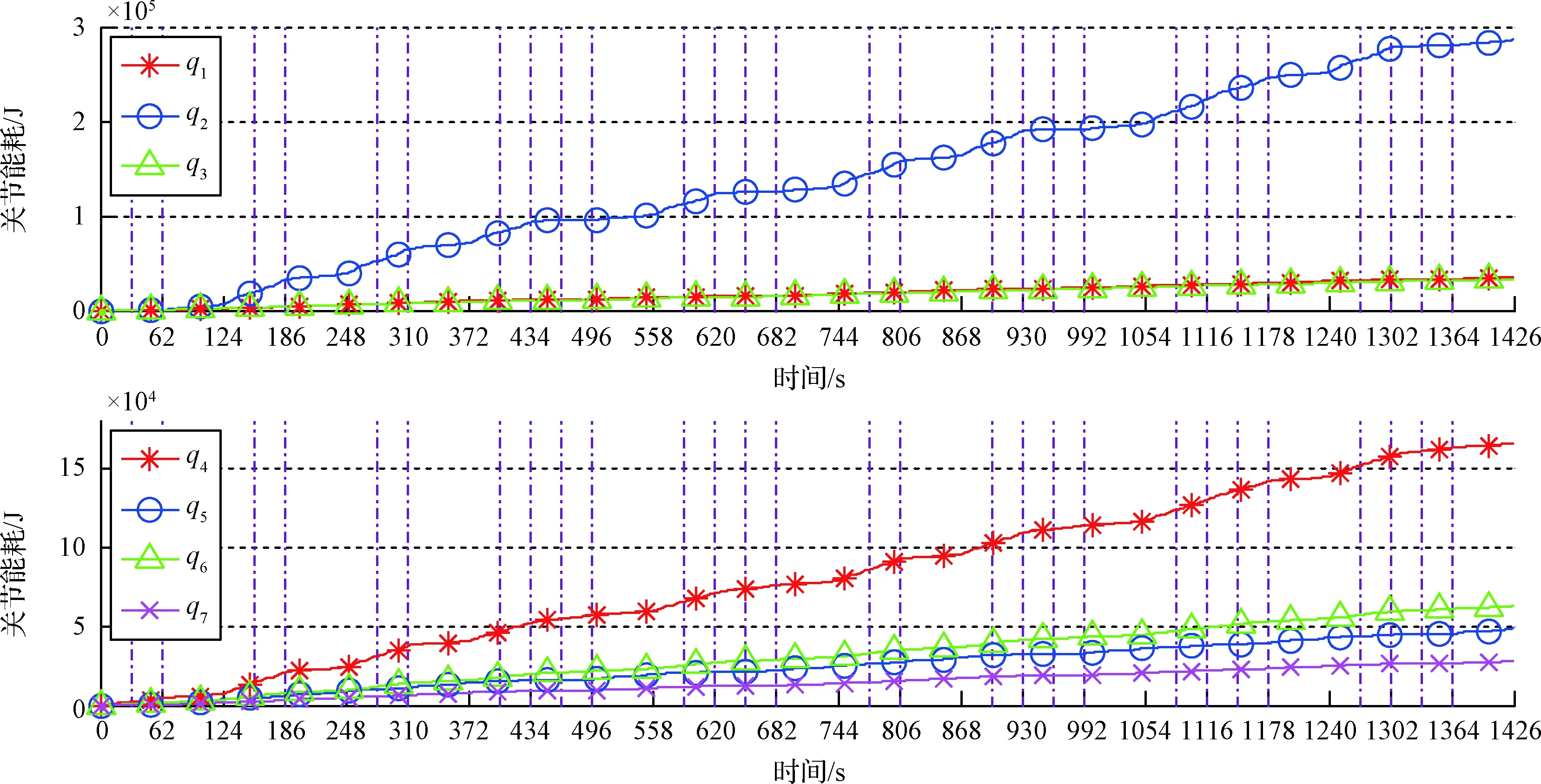
图21 整个装配过中的机器人关节能耗变化图Fig.21 Energy consumption in the whole assembly process

5 结 论

本文针对机器人在轨装配空间桁架结构的序列规划问题,提出了一种考虑机器人运动的序列规划方法。在求解装配单元最优装配序列的同时，可给出机器人装配过程中的规划与控制序列。首先，设计了在轨装配的机器人系统并对其建模；然后，设计了任务中机器人的运动规划与控制器，对机器人滑行步态、异杆跨越步态进行了仿真，关节角变化平稳、控制器跟踪准确，跟踪误差小；并以轴孔装配为目标，在装配出现误差且无视觉辅助的情况下，消除了误差影响，成功装配。随后，建立机器人在轨装配空间桁架结构的评价指标并寻优。在考虑装配可行性、装配稳定性、装配路径与装配能耗的影响下，在得到装配单元装配序列的同时，可得到机器人的运动，这对装配机器人设计与装配任务规划具有重要意义。