基于反例确认的CPS 不确定性模型校准*
杨文华 ,周 宇 ,黄志球
1(南京航空航天大学 计算机科学与技术学院,江苏 南京 211106)
2(高安全系统的软件开发与验证技术工信部重点实验室(南京航空航天大学),江苏 南京 211106)
3(软件新技术与产业化协同创新中心,江苏 南京 210093)
信息物理系统(cyber-physical system,简称CPS)涵盖了人、机、物的融合,它借助技术手段将人的控制延伸至信息与物理世界.CPS 涉及环境感知、嵌入式计算、网络通信和控制等系统工程,其目标是使物理系统具有计算、通信、精确控制、远程协作和自治能力.它注重计算资源与物理资源的紧密结合与协调,其应用领域非常广泛,包括工业控制、智能制造、智能交通、远程医疗、智能电网、航空航天等领域[1].研究CPS 对于相关领域软件的发展具有十分重要的意义.
CPS 需要融合像传感器、嵌入式计算、云计算、网络通信与软件等各类信息技术,设计时需要考虑如何对系统进行智能、安全、高效的控制,以完成复杂、精密的应用.与此同时,信息计算、物理设备、外界环境之间的复杂交互也需要得到关注,因此CPS 往往比较复杂.除此之外,由于系统与环境的固有复杂性以及系统中使用设备的不完美性,不确定性普遍且固有存在于CPS 中.例如,系统感知环境时使用的传感器就难免会存在误差,这一误差的具体值在运行时是不确定的[2,3].然而,CPS 的“身影”又广泛出现在大量安全与任务攸关领域,因此,如何在CPS 复杂性及不确定性影响下对其质量进行保障成为了CPS 研究的重点关注问题.形式化验证是保障系统质量的有效途径之一,它可以提供严格的证明来验证系统在运行过程中是否满足要求的性质.现有工作在CPS 的验证问题上取得了显著进展[4],对CPS 的安全性[5,6]及鲁棒性[7]等性质进行了验证.在这些验证工作中,模型检验技术是一类被广泛使用的技术[8].基于系统的模型与待检验的规约性质,模型检验技术可以自动化地对系统模型的状态空间进行显式的遍历或者以符号化的不动点计算来判断该模型的行为是否满足规约性质.当检查结束时,如果未出现反例,则该模型对于此规约性质而言一定是正确的;而如果出现反例,则模型检验技术会给出一个具体的执行轨迹,说明模型是在何种输入下如何一步步执行并最终违反给定的规约性质的.
不确定性广泛存在于CPS 中且会影响系统的执行.因此,在对CPS 验证时也需要考虑不确定性,否则会导致验证结果不准确,与系统实际运行情况存在偏差.一种通用处理不确定性的方法是对系统中的不确定性进行建模,刻画系统中不确定性的特性和影响,再在验证时融合系统模型与不确定性模型.例如,我们之前的工作[4,9]提出通过误差区间与分布对CPS 中的不确定性(如传感器感知误差)进行建模,之后借助约束求解器对系统进行验证,验证时将不确定性对系统感知变量的影响考虑进去.通过考虑这些不确定性,我们发现了已有验证方法不能发现的但系统实际运行中却存在的错误情况(反例),提高了验证结果的准确度.反例描绘了系统是在何种输入下如何一步步执行并违反规约的.但是由于受不确定性因素的影响,即使在给定的输入下反例也不一定能够被触发,因为我们无法控制不确定性的程度,比如报告的反例中要求传感器的误差是某个值,但系统在实际运行时传感器的误差却不一定满足反例的触发条件.因此,反例的发生是存在概率的,为此我们提出了一种估算反例发生概率的方法,可以提供更丰富的验证结果信息.
然而,验证的一个关键输入是不确定性模型,这些验证工作的有效性非常依赖于不确定性模型是否精确.倘若输入的不确定性模型不够精确,则势必会导致验证结果与实际不符.例如,我们使用误差区间与分布来刻画CPS 中的传感器误差这一不确定性,但是由于传感器的运行受众多环境因素的影响以及数据样本大小的局限性,实际中可能难以在最初就精确且完全地建模出这一不确定性,具体可以表现为误差区间不精确或者分布的参数有偏差.验证时使用不精确的不确定性模型会影响验证结果的准确度,比如报告的反例在现实中不会发生或者不太重要的反例可能被错误地突出报告(像低概率的反例被报告为高概率).为了消除不精确的不确定性模型对验证结果的影响,我们提出通过校准来得到精确的不确定性模型,从而提高验证结果的准确度.
首先,为了确认不确定性模型是否精确,我们观察到可以利用反例确认来进行判断.所谓反例确认就是让系统在反例要求的环境中运行,观察该反例是否会在系统执行中被触发.在反例的确认过程中,如果我们发现所报告的反例的概率与实际确认时统计的反例发生概率相差甚远,则可以认为不确定性模型不够精确,因为不确定性模型是计算反例概率的关键输入.例如,假设我们报告的一个反例,根据不确定性模型计算的反例发生概率为0.2,但在实际环境中对其进行确认时经过统计后发现,执行了100 次都没有观察到该反例的触发,则可以有足够的理由认为用于验证的不确定性模型不够精确.其次,在确认不确定性模型不精确之后,为了得到更准确的验证结果,我们提出了一种对不确定性模型进行校准的方法.该方法利用反例确认的结果来指导不确定性模型的校准.具体而言,就是将不确定性模型的校准问题化归为一个搜索问题,搜索的目标是最小化反例的计算概率与确认过程中的反例触发的实际概率之间的差异.通过遗传算法对该搜索问题进行求解,求解的过程中会不断改变不确定性模型(如区间范围以及分布的参数)以使得反例的计算概率与实际概率的差异最小化,之后将满足最小化的不确定模型作为校准后的模型.为了进一步确认校准后的不确定性模型是否精确,我们通过假设检验来帮助判断.我们使用校准后的不确定性模型重新验证系统,再对新报告的反例进行确认并对它们的计算概率与实际概率进行假设检验来判断这两种概率之间的差异是否足够小.若能通过检验,则接受校准后的不确定性模型并停止校准,否则,引入更多的反例确认数据,重复上述校准过程,直至通过检验.
本文第1 节介绍我们所使用的驱动案例,一个自动避障与搜索小车系统.第2 节详细介绍我们提出的不确定性模型校准方法.第3 节展示校准方法在驱动案例上的实验结果以及分析.第4 节介绍目前对CPS 中不确定性进行处理的相关工作.最后第5 节是总结.
1 驱动案例
自动小车是一类典型的信息物理系统[1].图1 展示的是一个自动小车系统的运行场景.小车的主要功能是探索整个区域并避免碰撞到任何障碍物.小车可以在方格内执行相应动作,移动到东南西北4 个方位的其他方格内.小车车身四周配备了传感器,可以感知四周障碍物的距离.为了确认小车对区域探索是否广泛,区域内设置了一些检查点,小车巡视到检查点时会收到相应信号.自动小车系统会基于感知到的距离来决定小车的探索动作并躲避障碍物.如果小车撞到障碍物,则认为自动小车系统失效,或者小车的运行步数超出了一个阈值却仍未巡视到所有检查点,这种现象也认为是失效.
小车系统的运行逻辑是系统设计的关键,为了应对这一问题,我们的已有工作[4]提出了使用交互状态机(interaction state machine,简称ISM)来建模系统的运行逻辑.ISM 被定义为一个元组M:=(S,V,R,s0),其中,S是系统所有状态的集合,s0∈S是系统的初始状态;V是包含系统所有变量的集合.V=Vs∪Vn,其中,Vs和Vn表示两个不相交的类别.Vs包含所有的感知变量,这些变量存储系统关注的环境属性值,Vn包含了其他所有变量,即非感知变量;R是系统所有执行规则的集合.对于每个规则r∈R,r关联到一个状态s∈S,该状态是r的源状态.规则r的形式是r:=(condition,actions),条件condition是一个逻辑公式,其涉及的变量都在V中,当公式被满足时,规则会被触发执行.动作actions规定了当规则被触发时应该执行的动作,这些动作可以更新系统状态也可以与环境进行交互(例如控制小车移动).系统通过ISM 模型是可以执行的.从初发状态s0出发,一个ISM 模型M:=(S,V,R,s0)重复地读取其感知变量的值(自动地通过传感器的环境感知更新),然后评估并决定执行何条规则,最后执行被选中规则的相应动作.当状态s∈S是M的当前状态时,以s为源状态的所有规则被启用,而其他规则被禁用.只有被启用的规则可以参与到规则的评估中,评估是依据环境感知来判断规则的逻辑公式是否被满足.若一个被启用的规则r的条件r.condition被满足,则该规则将被触发执行.当有多条规则的条件都得到满足时,只能有一条规则被选择执行,这可以通过一些优先级或随机机制来解决.因此,一个ISM 模型的一次执行可以表示为一条由状态和规则构成的路径σ=s0r1s1...rnsn.
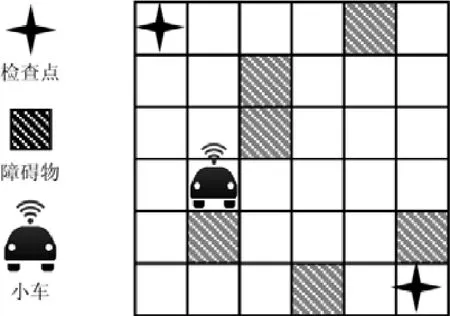
Fig.1 The running scenario of the robot-car system图1 自动小车系统运行场景
为了验证CPS 的行为是否正确,已有工作[4]基于ISM 使用模型检验技术对系统进行验证.具体而言,首先将ISM 模型中的路径取出,获取每条路径的路径条件(即路径中所有规则的条件的合取).由于系统与环境之间存在交互动作,系统执行完这些交互动作会影响系统后续的环境(例如小车往东移动后,与东边障碍物的距离会缩短),因此需要将这些动作的效果建模出来,具体可以建模为模型中感知变量之间的约束(例如小车往东移动前后与东边障碍物的距离之差应为小车东移的距离).另外,为了考虑系统中的不确定性,使用误差区间对其进行建模.例如,假设小车与东边障碍物的实际距离为east,但是受由于不确定性因素的影响,传感器存在一个误差区间[–6,6],因此小车感知到距离可能不是east,而是[east−6,east+6]范围内的某个值.在进行验证时,将路径条件中受不确定性影响的感知变量v替换为v',同时要求它们满足v–a≤v'≤v+b这一约束,其中,[a,b]是传感器的误差区间.最后,将更新后的路径条件、建模动作效果的约束以及失效条件一起输入到SMT(satisfiability modulo theories)约束求解器进行求解.详细的验证方法和过程可参见文献[4,9],这里不再赘述.若约束不满足,则说明路径正确,否则,说明此路径有问题,约束求解器也会给出一个反例,描述此路径对应的约束中所有变量的取值情况.反例对应的是系统的一次实际执行.以小车系统为例,根据小车系统的反例可以构造出一个实际的物理环境(如障碍物的分布).让小车在这一环境中运行,该反例却不一定会被触发,因为传感器的不确定性不受我们控制.因此,即使在反例对应的环境中,反例的触发也存在一定的概率.而这一概率与建模不确定性的误差区间有着密切的联系,不确定性在误差区间内如何分布会影响到反例的触发概率.因此,在建模不确定性时,不仅可以使用误差区间还需要使用概率分布.例如,传感器的误差可以是高斯分布或者均匀分布.依据这些不确定性模型以及系统模型,可以计算出所报告的反例的发生概率.反例概率描述的是在给定的输入下(以小车为例,即一个障碍物分布的具体实际场景),系统按照该反例规定的路径执行的概率.在这一过程中,我们不要求反例中某些变量的取值(例如运行时感知的误差)与验证时返回的值一致.文献[9]的工作中也给出了详细的计算方法.这些验证结果的信息非常丰富,可以为系统质量的提高和改善提供巨大的帮助.
可以看出,在这一验证过程中,不确定性模型起着至关重要的作用.不确定性模型不仅会影响报告反例的数量,还会影响反例的计算概率.以上述小车系统为例,传感器的误差范围实际应该为[–6,6],但在最初可能会得到[–5,5]这样一个范围.若验证时使用的是这样一个不精确的模型,显然会导致验证结果不准确,比如无法报告实际存在的反例.除此之外,建模不确定性的概率分布得也可能不精确.假设不确定性的实际概率分布为均值是0、方差为1 的高斯分布N(0,1),但最初建模时无法精确获得相关信息,使用的是均值为0、方差为4 的高斯分布N(0,4).由于估算反例发生概率时会用到不确定性的概率分布,使用这一不精确的模型,显然会导致反例概率的计算不够准确.因此,为了得到更准确的验证结果,需要对不精确的不确定性模型进行校准.
2 基于反例确认的模型校准方法
为了获取更准确的验证结果,我们的已有工作在验证CPS 时考虑了系统中的不确定性[9].相较其他验证方法,该方法可以检测到许多被其他方法忽略的真实反例.而该验证方法的一个重要输入是不确定性模型.建模不确定性时使用的是物理学中常用的误差区间与分布.以传感器感知的不确定性为例,在感知时传感器不可避免地存在误差,运行时我们却无法确认具体的误差值是多少.但这个误差一般存在一个大概的范围且常常可以用某种分布对其进行刻画.
然而,由于测量过程中不可控制的噪声和数据样本数量存在一定的局限性,很难在最初就精确而完整地建模系统中的不确定性[10].从而使得用于验证的不确定性模型不精确.这里,不确定性模型具体代表建模不确定性时所用的误差区间与相关分布的一些参数(如高斯分布的均值和方差).而这些不精确的模型会导致验证结果偏离现实:不太重要的反例可能被错误地突出显示(如本来低概率的反例变成了高概率),或者更糟的是,还有可能会报告一些错误的反例(如现实中不会发生).具体的表现形式可以是,所报告的反例的概率与实际中统计的反例发生的概率相差甚远,因为不确定性模型是计算反例概率的关键输入.不精确的不确定性模型会导致所报告的反例的计算概率与真实场景中统计的实际概率之间出现不一致.基于这一关键观察,我们提出通过反例确认,比较反例计算概率和执行中统计的实际概率之间的差异来发现不精确的不确定性模型,并基于反例确认的结果来进行模型的校准.接下来,我们将详细介绍所提出的不确定性模型校准方法.
2.1 方法概述
本节给出不确定性模型校准方法的概述,我们将校准问题表达为一个搜索问题,其目标是最小化反例的计算概率与实际概率之间的差异.方法的过程如图2 所示,主要包括识别、搜索以及判断这3 部分.首先,为了识别不确定性模型是否精确,比较反例的计算概率与实际概率之间的差异,如果它们之间的差异很大(大于给定的阈值),则认为不确定性模型是不精确的.在搜索阶段,采用基于搜索的算法来找到最小化适应度函数的解(即校准了的不确定性模型).基于搜索的算法可以根据现有的数据集提供自动评估,以评估校准的不确定性模型的质量.然而,仍然存在这些数据不具有代表性的可能,这将会导致校准的不确定性模型与这些特定数据过于匹配从而偏离了真实的不确定性模型.为了应对这个问题,我们采用假设检验来辅助判断校准后的模型是否精确且具有代表性.具体而言,我们使用校准后的不确定性模型再次对系统进行验证以获取新的反例.对新的反例,计算它们的发生概率并统计它们在实际场景中的实际发生概率,再通过假设检验判断反例的计算概率与实际概率之间的差异是否足够小.若能通过假设检验,则接受校准后的模型并停止校准.否则,引入更多的反例样本进行校准,并重复该过程,直到假设检验认可校准后的不确定性模型.

Fig.2 Overview of the calibration approach of uncertainty models图2 不确定性模型校准方法概述
2.2 反例确认
不精确的不确定性模型会导致验证结果偏离现实.反之,通过对验证结果进行确认,可以发现用于验证的不确定性模型是否精确.换言之,我们可以让系统在反例对应的实际场景下运行,统计反例是否会触发以及触发的频率.根据这些信息,可以获得反例的实际发生概率.然后将反例的计算概率与实际概率进行比较,就能识别出不确定性模型是否精确.
已有工作[4]通过遍历CPS 对应的ISM 模型的每条候选路径来收集系统的行为,并获取路径的路径条件,其中与环境相关的变量使用了误差区间来引入不确定性.失效条件描述了系统的故障,通过把失效条件与路径条件合取再使用SMT 求解器对条件进行求解可以得到验证结果.如果条件满足的话,则意味着系统会失效,而求解器返回的解与路径一起组成一个反例.反例描述了系统的执行轨迹,其中包含失效条件与路径条件中变量的取值,这些值可以对应到导致系统失效的环境输入.
验证结果的准确性对系统调试过程有很大的影响,因为不准确的验证结果会误导开发人员调试时的意图.在不准确的验证结果中可能会有虚假的反例,或者不太重要的反例被错误地突出报告.为了精化验证结果,确认(validation)是一种自然而广泛采用的方法.确认反例必须在反例描述的环境设置下实际部署并运行系统,观察系统是否遵循反例的路径执行并失效.反例中包含了丰富的信息,像系统每一步执行的动作以及相关输入变量的取值.根据这些信息可以构造出一个系统实际的运行场景.例如,自动小车系统的一个反例就可以对应到一个实际的物理场景,包括障碍物的分布以及检查点的位置等.下面我们以一个简单的示例来加以说明,针对一个反例,如何构造与之对应的一个实际的场景.图3 展示的是一个简化的反例及其与之对应的场景.我们规定的性质是要求小车不要撞上障碍物,由于这里我们主要关注的是如何根据反例构造一个实际的环境,因此给出的并非一个完整的反例,实际的反例往往比这复杂且会违反性质.假设我们通过验证找到这样一个反例,该反例的路径如图3 所示,其中包含一条规则r1.而r1.condition要求小车与北边障碍物的距离大于2,r1.actions描述的动作是往北移动一个单元.针对这条路径中包含的变量north,求解器返回的值为3.路径以及变量取值构成了一个反例,而对于这个反例,我们可以构造出图中所示的实际场景,在小车往北移动之前,根据north的取值可知,距小车北边3 单元有一障碍物,因此我们可以构造出图中所示的场景.

Fig.3 An example of the environment construction for a counter example图3 反例对应的环境构造示例
反例中包含的信息十分丰富,根据反例如何构造实际场景亦很直观,因此这里不再赘述.而反例确认就是让系统在该反例对应的实际场景下来运行,观察反例能否触发.在观察的过程中,我们还可以记录系统运行的次数以及每一次的运行情况,从而可以统计出反例的实际概率.若通过比较反例计算概率以及实际概率发现两者之间的差异较大,则可以安全地判断出不确定性模型不够精确,需要进一步校准.
2.3 校准问题求解
为了校准不精确的不确定性模型,我们提出将校准问题转化为一个搜索问题.给定一组具有实际概率和计算概率的反例,搜索以已有验证中使用的不确定性模型作为起始点,搜索能够最小化适应度函数的不确定性模型.而适应度函数是关于反例的实际概率和计算概率之间的差异.更具体地,不确定性模型是使用误差区间与分布进行建模的,而这些又表征为具体的参数,例如高斯分布的均值和方差.因此,搜索问题的本质就是找到最小化适应度函数的不确定性模型参数的值.下面,我们详细介绍适应度函数的定义以及所使用的搜索算法.
2.3.1 适应度函数的定义
适应度函数描述的是搜索问题的目标,并通常根据相关的度量标准或属性而加以定义.如前所述,校准需要首先发现所选反例的计算概率和实际概率之间的不一致性.我们通过计算这两种概率之间的差异,并使用其绝对值的总和除以反例的个数来描述不一致性的程度.由于我们的目标是找到适当的误差区间和分布的参数值,使得所选择的反例的计算概率与实际概率之间的不一致最小化,所以我们直接将上述计算不一致性的函数作为适应度函数.为了获得反例的实际概率,我们让系统在反例相应的环境中运行固定次数,并统计反例的触发次数.那么触发次数与总次数的比值就是反例实际的概率.由于反例的个数可能很多,所以获取所有反例的实际概率可能是非常耗时与不实际的,所以我们只选择了一部分反例来作为样本.选择反例的策略可以有很多,但是我们建议先选择具有高概率的反例,这样可以加快校准过程.
设U=(u1,u2,...,um)是包含不确定性模型所有参数的一个向量,Θ={σ1,σ2,…,σn}是选择的反例的集合.每一个u i∈U(1≤i≤m)可以是误差区间的上下限或者表征概率分布的参数,这些参数是在连续区间上取值的.例如,表征高斯分布的参数是均值和方差,表征均匀分布的参数是区间的下限和上限.每一个σi∈Θ(1≤i≤n)具有一个根据不确定性模型U计算得到的计算概率cali,还有一个从确认过程中得到的实际概率acti.适应度函数用于衡量所选反例的两种概率cali和acti之间的差异,其定义如公式(1)所示.由于具有多个反例,我们使用反例概率差异的平均值作为适应度函数,其中,n是反例的个数.适应度函数是搜索的目标指导,在这里我们校准问题的目标是最小化适应度函数的值.

2.3.2 搜索算法
在基于搜索的软件工程相关研究中有许多优秀的搜索算法,如爬山算法、模拟退火和遗传算法等.这些算法具有不同的特征,可用于不同的场景.例如爬山算法与模拟退火被认为是局部搜索算法,它们每次参考一个候选解进行操作,并在该候选解的附近选择移动[11,12].另一方面,遗传算法被认为是全局搜索算法,可以一次在搜索空间中抽取多个点,相比局部算法提供了更强的鲁棒性[13].因此,在我们的问题中使用遗传算法进行搜索.遗传算法的过程从一组随机选择或预定义的个体开始,它们组成了第1 代种群.之后,种群可以通过重复地选择、交叉和变异等操作进化以找到取得最优值的个体.而评估个体与最优解的接近程度是使用一个适应度函数.设计遗传算法有几个关键组成部分,如选择操作(即如何选择个体进行复制)、交叉操作(即如何从两个父代生成子代)、变异操作(即如何变异一个子代)和初始种群生成(即如何生成第1 代种群).
我们使用遗传算法求解校准问题,其过程如算法1 所示.算法的输入包括不确定性模型U、选定的反例的集合Θ、作为算法中主迭代过程终止条件的一个整数n和一个小实数 .ϵ算法生成一个固定个体数的初始种群,按照MATLAB 中给定的建议[14],当适应度函数中的变量数不大于5 个时,初始种群数可以设为50,超过5 个时可以设为200 或者根据个数设成更多.种群规模也可以根据经验进行调整.增加种群数量使得遗传算法能够搜索更多的点,从而获得更好的结果.然而,种群规模越大,遗传算法计算每一代的时间就越长.一种常见的生成初始种群中的个体的方法是从适应度函数中的每个输入变量(即U中的每个元素)的取值范围内随机地选择一个值.然而,这种方法忽略了已有的不确定性模型,尽管已有的模型在某种程度上并不精确,但仍然比随机选择的值具有更大的可信度.
算法1.基于遗传算法的校准.
输入:不确定性模型U,选择的反例集合Θ,最大迭代次数n,阈值ϵ(用于衡量两次连续评估值之间的差异);
输出:校准后的不确定性模型s.


换句话说,现有的不确定性模型是不精确的但并不是完全错误的,所以要搜索的精确的不确定性模型应该接近现有的模型.因此,我们基于现有的不确定性模型来生成初始种群.首先,将不确定性模型U中所有变量的值编码成二进制形式.之后,对于每一位以一个概率pm随机地改变其值(从0 改为1 或从1 改为0),pm的取值后续将加以讨论.算法的核心部分是其迭代过程(Lines 5~13),其中,种群进行进化并且个体依据它们的评估值被选择.当达到最大迭代次数n,或者种群的最佳评估值不再显著变化(即两个连续迭代的最佳评估值之间的差小于ϵ)时,搜索终止.然后,最适合的个体被解码,以获得输入变量的值,它形成了校准的不确定性模型.
在迭代过程中,有几个关键的操作:选择(Line 9)、交叉(Line 10)和变异(Line 11).下面我们详细加以介绍.
· 选择.它根据评估值为子代个体选择父代个体.对于每一个个体i,其评估值evali就是适应度函数以个体i为不确定性模型的函数值fit.我们采用了一种标准的选择方法(轮盘赌方法),其中,个体i被选择的概率是evali是个体i的评估值,m是个体的总个数.被选择的个体都在选择池中.
· 交叉.它通过交叉两个父代个体来为新种群形成两个新的子代个体.为了选择交叉的父代,给定一个交叉概率pc,我们随机地从选择池中选择pm×m/2 个父代.在具体的交叉操作中,单点交叉策略被应用.然后,选择池中父代被其子代所代替.
· 变异.它通过对种群中的个体进行小的随机改变来提供遗传多样性,并使遗传算法能够搜索更广阔的空间.我们逐个地对选择池中的个体加以选择,并以变异概率pm随机更改其字符(例如,将以二进制形式编码的个体的字符从0 改为1).
遗传算法的参数(例如,交叉概率pc与变异概率pm)设置是问题依赖的.一般来说,增大变异概率可能会增加遗传的多样性,但会导致搜索过于分散在解空间上,从而增大了交叉概率,可导致算法在解空间上相对集中的区域进行搜索.我们也可以根据实验的反馈来调整参数.同时,现有的文献总结了许多有价值的经验,供我们处理问题时参考[15].根据建议,从[0.4,0.9]与[0.0001,0.1]中分别选择交叉概率和变异概率的值是安全的.算法获得的解包含了表示校准的不确定性模型的参数变量的值.
2.4 假设检验
在我们校准不精确的不确定性模型之后,确定是否接受校准的模型仍然是一个问题,因为尽管适应度函数可以评估校准的模型在现有数据样本上的质量,但该模型可能会过度匹配于这些数据.为了解决这一挑战,我们引入了新的反例数据样本,并采用假设检验来帮助我们判断在这个新的数据样本中是否有足够的证据来推断校准的不确定性模型对总体是精确的.假设检验是用来判断样本与样本、样本与总体的差异是由抽样误差引起的还是本质差别造成的统计推断方法[16].其基本原理是先对总体的特征做出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受做出推断.假设检验检查两个对立的关于总体的假设:原假设(H0)与备选假设(H1).原假设是待检验的推断.根据从样本数据获得的检验统计量,测试确定是否接受或拒绝原假设.就我们的问题而言,想用假设检验来回答的问题是校准的不确定性模型是否足够精确.如前所述,有理由认为,当不确定性模型精确时,反例的计算概率与实际概率之间不应存在明显的差异.基于该观察,我们提出H0与H1.对于一组未用于校准的反例σ1,σ2,...,σn,我们利用校准后的不确定性模型计算每一个反例σi(1≤1≤n)的概率cali,并在实验中获取其实际概率cati.如此一来,便得到了n对独立的观察数据:(cal1,act1),(cal2,act2),...,(caln,actn).设di(1≤1≤n)是σi的计算概率与实际概率之差,即di=cali–acti.由于每一个di都是由不确定性模型与精确的模型之间的偏差导致的,依据统计理论,则可以安全地假设它们服从一个正态分布.假设i=1,2,...,n,即d1,d2,...,dn是总体为的一个样本,其中,未知.基于这个样本,需要检验假设H0:μd=0与H1:μd≠0.H0表示反例的计算概率和实际概率之间没有显著差异.相反地,H1表示它们之间存在显著差异.下面,我们需要检验是否可以接受H0.如果接受,我们可以有信心地得出结论:校准的模型是足够精确的,并据此停止校准过程.否则,我们将引入更多的实验样本来进行校准,并重复校准过程,直到假设检验认可校准的不确定性模型.
我们在假设检验中采用的是经常使用的p值方法.p值被定义为在原假设成立的情况下获得与实际观察到的结果相同或“更极端”的概率.在此方法中,我们首先为原假设H0的p选择一个阈值α,该值被称为检验的显著性水平,一般设为5%或1%.如果p值小于或等于选定的显著性水平(α),检验表明观察到的数据与原假设不一致,因此原假设应该被拒绝.否则,接受原假设.例如,使用一个常用的α=0.05,当p<0.05 时原假设被拒绝,当p>0.05 时接受原假设.因此,p值的计算是我们假设检验的关键步骤.为此,我们首先需要确定一个检验统计量.存在许多检验统计量(如paired tests、Z-tests、t-tests 和Chi-squared tests),其选择是问题依赖的.例如,Z-tests 适用于检验严格服从正态分布且标准差已知的总体的均值.而t-tests 适用于在更宽松的条件下(假设更少)检验均值.使用检验统计量的观察值与其已知的分布,即可以计算p值.例如,为了对一个服从高斯分布N(μ,σ2)(其中,σ未知)的总体的均值μ进行假设检验,其中待检验的假设是H0:μ=μ0,H1:μ≠μ0.我们使用被现有工作[16]广泛采用的检验统计量其中,是样本的均值,S是样本的标准差,n是样本的数量.假设从样本数据中计算的检验统计量t的值是t0,则当t0大于0 时,p值等于,当t0小于0 时,p值等于许多现有的统计工具都支持p值的自动计算.在我们的检验中,也应用相同的方法来计算p值.用与表示样本d1,d2,...,dn的均值和方差.根据样本的特性,我们也使用检验统计量然后替换相应的值得到.之后我们可使用上述讨论的方法来计算其p值,并与显著性水平α进行比较,在我们的问题中将其设为5%.如果p值大于α,则检验表明反例的计算概率与实际概率之间没有明显的差异,故而可以接受原假设.在这种情况下,我们接受校准后的不确定性模型,并认为其够精确.如果p值不大于α,则检验表明反例的计算概率与实际概率之间存在明显的差异,应该拒绝原假设,不确定性模型也需要进一步校准.这需要新的反例并获取其计算概率和实际概率,这一过程可能是耗时的.不过,幸运的是,在假设检验中,我们已经有了一个新的反例样本,显然它们包含我们校准所需的新的信息(计算概率与实际概率).因此,我们直接引入这些反例并重新校准不确定性模型.
3 实验评估
本节评估校准方法的有效性,具体考虑以下两个研究问题.
研究问题1:我们的方法能不能有效地校准不确定性模型?
研究问题2:与其他算法相比,我们校准中使用的遗传算法表现如何?
在评估中我们使用第1 节介绍的驱动案例作为实验对象.该CPS 使用ISM 进行建模,详细的ISM 模型取自文献[4,9].借助已有工作中的验证方法,可以对该自动小车系统进行验证,获取系统的反例并计算出这些反例的概率.
3.1 校准的有效性
本实验评估的是采用我们的方法校准CPS 中不精确的不确定性模型的有效性.为了评估校准的有效性,我们首先需要得到不精确的不确定性模型,进行校准后再与精确的模型进行对比.实验中,校准的不精确的不确定性模型是在已有的一个精确的不确定性模型上改变得到的.在我们已有的工作[4]中,通过大量针对自动小车系统的实验可以发现,使用的一个已有的不确定性模型可以准确地估算反例的概率.因此可以认为这个已有的不确定性模型是足够精确的,我们也用其作为实验中的精确的不确定性模型的基准.不精确的不确定性模型是在这个模型(误差区间为[–6,6],分布为高斯分布N(0,22))的变化上得到的.
具体来说,我们识别了3 个控制变量:误差区间以及分布的均值和方差.这些变量的变化是以每次改变一个变量的受控方式进行的,我们对这些变量分别单独增大或减小了±1 与±2,即每个变量都进行了减小1 或2,增大1 或2 共4 种变化.通过一系列实验来检查我们的方法是否可以成功地校准那些不精确的不确定性模型.基于自动小车系统的反例来校准不精确的不确定性模型,自动小车系统的每个反例都具有计算概率和实际概率.计算概率是用不精确的不确定性模型计算得到的,实际概率是从实验中统计获得的.然后,将这些不精确的不确定性模型与反例一起传递给我们的校准方法进行校准.
表1 展示的是在驱动案例上得到的实验结果.实验中,对于使用不精确的不确定性模型得到的反例进行了确认,可以识别出这些反例的计算概率与实际场景中统计得到的实际概率之间差异较大,因此我们对其进行了校准.我们将精确的不确定性模型作为评估校准后模型的基准,而第2 列为校准后的不确定性模型.为了比较两个不确定性模型,使用欧氏距离来表示两个模型之间的差异.误差区间的下限l、上限u、均值n和方差v组成了模型m的4 个维度,两个模型m1与m2之间的欧式距离d是我们提出使用函数c=1/(1+d)来评估两个不确定性模型的接近度.显然,c的取值范围是(0,1],两个模型之间的距离越小,c值越大.如果两个模型完全一样,则c=1.从表1 第3 列我们可以看到,根据模型改变的不同,不精确的不确定性模型与精确的模型之间其接近度从0.077 到0.500 之间变化(平均为0.309).另一方面,校准后的不确定性模型显示出它们与精确的模型之间的接近度有了显著的改进(如第4 列所示).校准后模型的接近度从0.552 到0.757之间变化,平均接近度是0.689,提高了122.7%,这表明,校准后模型的精度已经大大提高,且接近精确模型的水平.我们还记录了适应度函数评估的迭代次数和遗传算法搜索的消耗时间,分别见表1 第5 列和第6 列.我们利用假设检验来帮助确定校准的不确定性模型是否足够精确且具有代表性.如果检验没有通过的话,则每次多引入10 个反例到校准过程中并重复校准,而这会增加搜索消耗的时间.引入的新反例的实际概率也需要通过反例确认的实验统计获得.在真实场景中,我们对这些反例同样也执行了100 次以获取其实际概率.然而,如表1 第7列所示,我们的方法需要的假设检验轮数很少.

Table 1 Calibration results obtained using data from real scenario on the motivating example表1 在驱动案例上使用真实场景中的数据获得的校准结果
在统计反例的实际发生概率时,需要让系统在反例对应的实际场景中多次运行,观察反例是否会触发以及触发的次数,为了使统计的概率尽可能地准确,运行的次数应该尽可能地多.但是,由于在实际场景中反复确认反例的成本较大,因此为了获取更准确的统计概率,我们在模拟场景中也对反例进行了反复的确认.在模拟实验中,我们对每个反例执行了1 000 次以统计其实际概率.另外,模拟实验还有一个好处是我们可以改变模拟实验中精确的不确定性模型,观察校准方法对这些不同模型的校准是否也有效.表2 报告了使用从模拟实验中统计获得的反例的实际概率进行校准后得到的结果,其中前4 个模型的变化基于的精确的不确定性模型是:误差区间[–6,6]、高斯分布N(0,22).中间4 个模型的变化基于的精确的不确定性模型是:误差区间[–6,6]、高斯分布N(1,22).后4 个模型的变化基于的精确的不确定性模型是:误差区间[–6,6]、高斯分布N(0,32).可以看出,上述真实场景下的实验结论在模拟实验中也一直保持一致.
需要注意的是,接近度的取值范围为(0,1],作为一种评估标准,它的值越接近1 就代表校准的模型与实际的模型越接近.借助假设检验来帮助我们判断何时停止继续校准,因此只要通过检验就停止校准.这是一种折中的做法,因为实际上我们可以通过增加反例样本的数量不停地重复校准.实验中假设检验的结果表明,根据校准结果得出的反例概率与计算的概率比较接近,所以我们没有进一步校准,若要获得更准确的模型,可以通过增加校准时使用的反例数量,或者提高假设检验的标准,来达到这一目的,但与此同时,相应的校准成本也会上升.
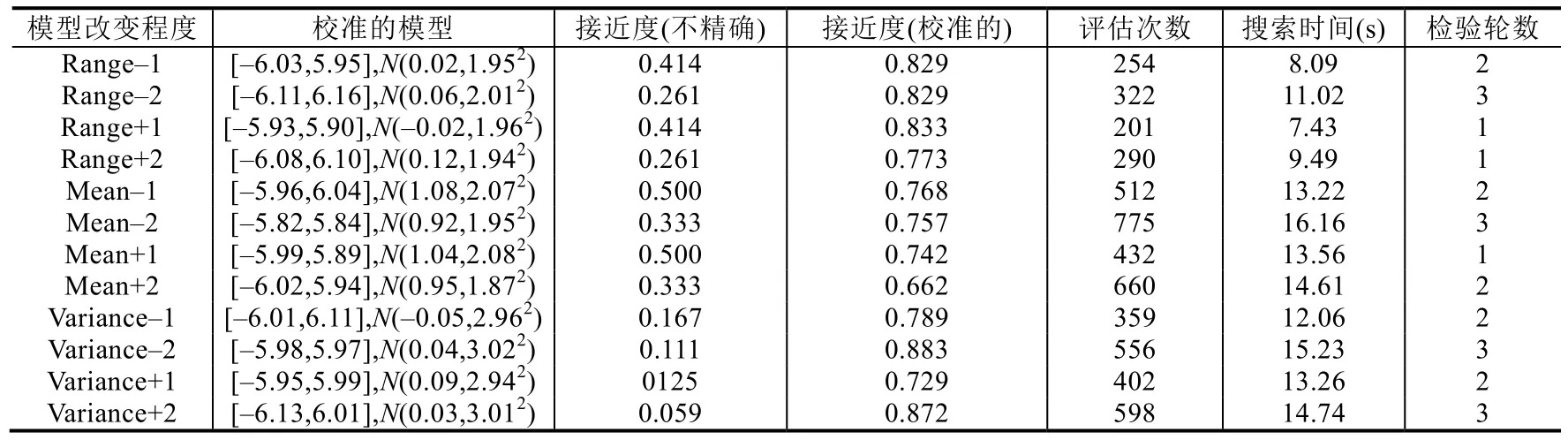
Table 2 Calibration results obtained using data from simulation on the motivating example表2 在驱动案例上使用模拟场景中的数据获得的校准结果
3.2 校准算法比较
我们通过使用遗传算法来搜索使适应度函数最小化的不确定性模型参数的值,以此来求解校准问题.除遗传算法外,还可以选择他算法用于解决这个问题,比如确定的分析方法或其他搜索算法.因此,为了进一步评估方法,我们将遗传算法与其他方法进行了比较.具体地,选择了另外3 种具有代表性的算法来求解这个问题:一种基于置信域的分析方法[17]、爬山算法[18]和模拟退火算法[19].
分析的算法是基于常用的置信域方法,在优化中常被用于表示使用更简单的与模型函数近似的目标函数的域的子集.然后通过近似模型函数和置信域,将原始问题转化为更简单的置信域子问题.我们在实验中直接使用MATLAB 优化工具箱中的“fminunc”求解器提供的分析方法来加以实现.同时,我们实现了爬山算法和模拟退火算法,以搜索不确定性模型参数的值,从而使适应度函数最小化.所采用的爬山算法是一个标准的爬山算法,初始搜索点设定为原始的不精确的不确定性模型的值.对于模拟退火,除初始搜索点也设置为原始不精确度不确定性模型的值以外,还有其他几个参数,包括初始温度、降温速率和迭代次数.参照文献[19],初始温度应该设置得足够高,而降温速率应略小于1.因此,我们尝试了几个不同参数的值以获得更好的性能,最终选择了100作为初始温度、0.96 作为降温速率以及20 作为迭代次数.在比较实验中,只用其他3 种算法代替了我们的遗传算法.我们的校准方法的其余部分,包括假设检验仍然保持不变.
我们再次使用了驱动案例作为实验对象,精确的不确定性模型是:误差区间为[–6,6]、高斯分布为N(0,22).用于校准的反例的实际概率来自于真实场景.表3 展示了4 种不同算法的校准结果.在每一个含有数据的单元格中包含3 个数字.第1 个是校准后的不确定性模型与精确的模型之间的接近度,第2 个是求解问题的计算时间,第3 个是假设检验的轮数.在我们的方法中,当校准的不确定性模型被拒绝后,需要更多的反例作为额外的样本来重复校准过程,并且需要准备反例的计算概率和实际概率.然而,重复校准过程将花费更多的计算时间,而这也包括在总的计算时间内.当校准结果被假设检验拒绝5 次时,我们将终止校准过程.表格中我们使用符号“#”表示没有获得校准的结果.
从表中我们可以看到,一般来说,基于遗传算法的方法的求解比其他3 种方法执行得更好,即遗传算法在更短的时间内计算了更精确的不确定性模型.更具体地说,由于适应度函数比较复杂,所以分析算法的能力比较受限,因为它需要执行置信域计算和因式分解.它往往花费了更多的计算时间.爬山算法在一次迭代搜索中花费的时间较少,但其常常落在局部最优中,这使得校准的不确定性模型容易被假设检验多次拒绝,需要重复校准,最终其总计算时间仍多于我们的方法.如实验结果所示,爬山算法给出的12 个校准不确定性模型中的9 个被假设检验5 次.模拟退火算法比爬山算法略好,但仍遇到类似的问题.基于以上讨论的实验结果可知,我们的基于遗传算法的校准方法可以有效地校准不确定性模型.
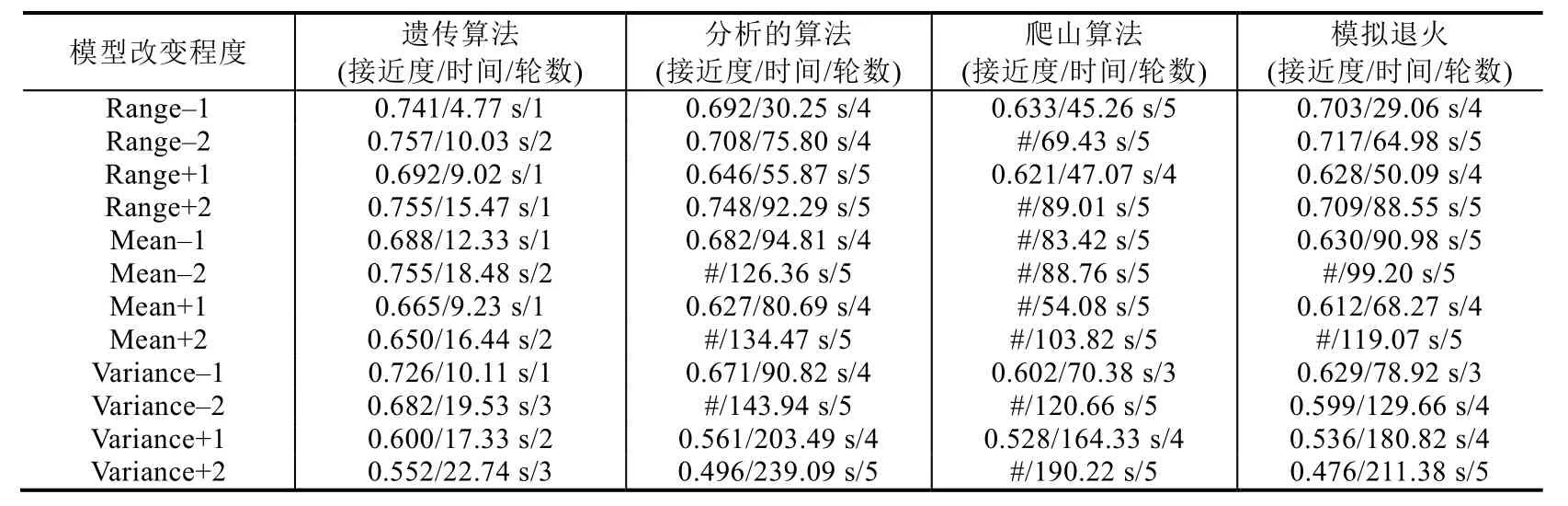
Table 3 Comparison of different algorithms in solving calibration problems表3 不同算法求解校准问题的比较
3.3 讨 论
本文所提方法的有效性可能会受到方法中随机性的影响.随机性的来源主要是方法中对于反例实际概率的统计以及校准时搜索使用的遗传算法.为了减小它们对实验结论的有效性影响,我们采取了一定的措施,具体而言,对于实际概率统计中存在的随机性,为了使统计的反例的发生概率与实际尽可能地相符,我们对每个反例在实际环境中进行了100 次的运行以统计其发生概率,同时也在模拟环境中运行了1 000 次.对于校准时搜索使用的遗传算法自身存在的随机性,我们在实验阶段根据已有工作的指导经验以及多次实验,对算法的参数进行了审慎的选择.我们的方法中包含的假设检验的部分也能起到降低随机性影响的作用.另外,本文处理的不确定性主要是传感器的感知误差这类不确定性,对于其他,例如动作执行缺陷等不确定性,需要在未来工作继续加以进一步研究.
4 相关工作
由于CPS 的自身特征以及环境的复杂性,在CPS 的许多方面都可观察到不确定性的存在.文献[2]研究了信息物理系统中不确定性的分类,并按照5C 技术架构[20]对CPS 中的不确定性进行了分类,介绍了架构中各层次上可能存在的不确定性.这些不确定性是CPS 中固有存在的,在CPS 的设计与实现过程中需要对其进行考虑与处理.若未妥当处理,不确定性很可能会影响CPS 的正确运行,进而导致系统出现各种问题.验证是一种有效的质量保障方法,已有工作通过在验证CPS 时显式建模不确定性,可以发现系统中许多潜在的问题.但验证时使用的不确定性模型却很难在最初就对其进行精确建模,因此本文提出了一种不确定性模型校准方法.本节将主要介绍与之相关的研究工作,具体包括CPS 中不确定性处理以及模型校准方面的工作.
尽管研究不确定性很重要,但CPS 中不确定性的研究仍处于发轫之初.为了深入理解CPS 中的不确定性,Zhang 等人[21]通过回顾各领域不确定性的现有工作,得出了一个不确定性的概念模型.该概念模型映射到CPS的3 个逻辑层次:应用层、基础架构层和集成层.他们使用UML 类图以及OCL 约束来表示该模型.为了确认该模型,他们在两个不同的工业案例上对不确定性进行了识别与描述.为了进一步描述CPS 中的不确定性,研究人员提出了多种不确定性建模方法.Cheng 等人[22]提出了一种需求语言RELAX,通过软件工程师明确指定系统需求中的不确定性以对其进行处理.该语言采用的是一种附带布尔表达式的结构化自然语言形式,使用威胁建模的一种变体来识别不确定性,其中威胁是在开发时带来不确定性的各种环境条件.文献[23]用SysML 需求图描述了CPS 中的不确定性,并借此在软件制品中追踪不确定性信息.CPS 涉及人、机、物的融合,为了刻画CPS 中人的不确定性行为,文献[24]提出了一种时钟约束规范语言的概率扩展.CPS 中的不确定性可能会影响系统的运行并可能导致严重的后果,发现问题的一种选择是测试不确定性对CPS 的影响.为了支持面向不确定性的CPS 的模型驱动测试,文献[25]提出了一个框架,以创建测试就绪(test ready)模型,该模型包含CPS 预期行为以及系统执行环境,并可以用于直接生成测试用例.验证是发现不确定性给CPS 带来的可能问题的另一种途径.CPS相关的验证工作较多[5,7,26-28],但只有一些工作[4,9]在验证中明确考虑了不确定性对系统的影响.我们之前的工作基于ISM 模型对CPS 进行了验证,并在验证中通过误差区间以及概率分布对不确定性进行了明确建模,相比其他不考虑不确定性的验证方法取得了更准确的验证结果.但正如之前所述,用于验证的不确定性模型的精确度难以保证.
校准是一个通用的术语.在物理学中,它可以用来表示评估和调整测量设备的精度与精度的行为[29],应用到不确定性模型的校准中,一种直接的思路是通过直接测量不确定性的参数来校准不确定性模型.与之互补,本文采取的校准思路是通过观察不确定性影响的最终结果来校准不确定性模型.通过直接测量来校准不确定性模型可能导致的一个问题是,通过直接测量校准后的不确定性模型验证得到的反例可能会与实际的差距较大.而我们的校准思路则从结果出发,是结果驱动的.我们根据系统最终的运行结果来校准不确定性模型,以使得通过校准后的不确定性模型得到的验证结果更接近实际,在这个过程中,不确定性模型蕴含的影响可能不仅仅是自身的.统计学中,也可以表示回归的逆过程或者统计分类中用来确定类成员概率的过程[30].在我们的问题中,它是指调整不确定性模型的参数,以确保模型尽可能精确地建模出实际的不确定性.一类与之相关的工作是模型校准(model calibration),其目标是系统地调整模型参数,使得输出能够更准确地反映现实[31].Vanni 等人在文献[32]中总结出了模型校准中的常见过程:识别要校准的输入,识别校准的目标,度量拟合适应度(评估输出与观察数据的匹配程度),搜索参数并接受校准结果.该过程的关键部分是适应度的度量和参数搜索策略.在现有工作中,最常用的适应度度量是最小二乘法、加权最小二乘法与似然函数[33].本文在校准过程中引入了适应度函数,使用的度量类似于最小二乘法.在参数搜索策略方面,有各种各样的方法来解决不同类型的搜索问题,例如广义的约减梯度法[34]、模拟退火[19]和遗传算法[13]等.贝叶斯方法也用于过模型校准[35],它定义了模型参数集的先验分布,并通过贝叶斯定理更新先前的结果,以反映在数据的似然函数中给出的附加信息,由此给出后验分布.为了实现这一点,可利用马尔可夫链蒙特卡罗的方法从模型参数的联合后验密度函数生成样本[35].
5 总结
CPS 的使用场景很多都是安全攸关的,对系统的质量有着较高的要求.而不确定性会影响到CPS 运行的方方面面,若未对其进行妥当处理很可能会对系统质量产生极大的负面影响.验证可以用于研究不确定性对CPS质量的影响,及早发现系统中的问题.已用工作在这一问题上取得了一些进展,验证CPS 时通过建模不确定性明确考虑了不确定性对系统的影响,相比传统方法取得了更为准确的验证结果.然而,由于测量过程中不可控的噪声和数据样本数量不足,很难在最初就精确地建模系统与环境之间交互的不确定性.本文提出了一种校准CPS中不精确的不确定性模型的方法,该方法利用当不确定性模型精确时反例的计算概率应与实验中统计获得的反例的实际发生概率接近这一观察,将不确定性模型的校准问题转化为一个搜索问题.之后,利用遗传算法来求解该问题,找到使得反例的计算概率与实际概率差异最小的精确的不确定性模型.同时,借助假设检验判断校准后的不确定性模型是否足够精确且没有过于匹配于选定的反例.基于实际案例上的实验结果表明,我们的方法能够有效地校准不精确的不确定性模型.

