运筹学存储决策问题在矿业企业生产中的运用

文金忠

（贵州省煤矿设计研究院有限公司，贵州 贵阳 550025）

运筹学经常应用与生活生产之中，在生产过程中产生的确定性以及概率相关的问题，需要进行改良与完善的策略。在学术研究中，运筹学的重要特征就是将约束性条件进行参数优化，从而达到满足生产要求的目的。关于这次研究，从文献中获取相关的知识以及学科方法，从而配合实际生产应用[1]。

在生产过程中，可以充分的实现运筹学的方法探索，经过调查分析发现，形成矿业中的普遍应用。基于矿业生产的复杂性以及技术性的要求，需要多种运筹学方法的尝试。根据非线性与线性之间的区别于联系，进行合理的动态调控，在使用方法的过程中，最重要的是通过计划延伸，并且强调混合规划的模型方法。应用过程中，了解矿石的储备，采矿的效益，通过时间等多方面的影响因素，进行产品的定位以及生产力成本的技术性创新，保持调查过程中的动态规划以及生产能力的调控，最大限度上提升生产效率和经济效益[2]。

1 提出问题

盘江煤电矿业公司井巷工程涉足拱架、锚杆等产品技术领域。集团公司从产品开发，产品销售直至井下专业化的安装、制作等多项服务。

非线性的井下支护系统是公司的主要产品之一。“非线性”系统是用于煤矿井下支护安装的设备。主要用来完成井下支护形式的形成。

目前，公司的“非线性”产品的核心硬件为拱架（产品1）、锚杆（产品2），均是由外地购进，如何订货才能使公司的成本最低是在年初计划时必须解决的问题。具体统计数据如下：

表1 两种非线性”产品的订货量及成本数据

2 建立问题模型

由于该产品的订货折扣是一定的，且在实际销售过程中并不要求必须是现货供应，且认为需求是连续均匀的。又因为企业可认在存储降至零后，还可以再等一段时间然后订货，主要是煤矿井下掘进的施工进度跟不上，当顾客遇到缺货时损失很小并且顾客会耐心等待直到新的补充到来。缺货会给公司带来直接或间接的损失，可以权衡得失，寻找最优的库存策略使总费用达到最小。这正是允许缺货的经济订货批量模型（允许缺货模型）此研究的问题。因此，用允许的经济订货批量模型（允许缺货模型）来求解。

3 求解模型，产生结果

（1）对于产品1。有D=R=1800套/年，C1=15800元/套年，C3=3000元/次，C2=1400元套/年。求得最优订货批量：

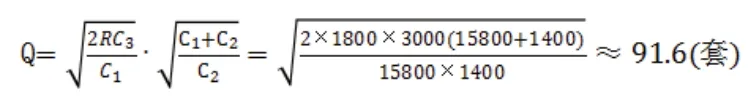
求得最大缺货量：

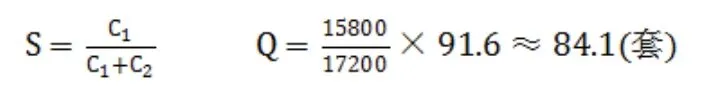
每年订货次数为：

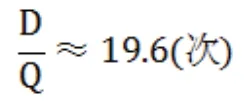
由于非整数，所以分别以19次和20次讨论其总费用，选择最佳次数。

a.订货次数为19次：

求得一年的总费用：

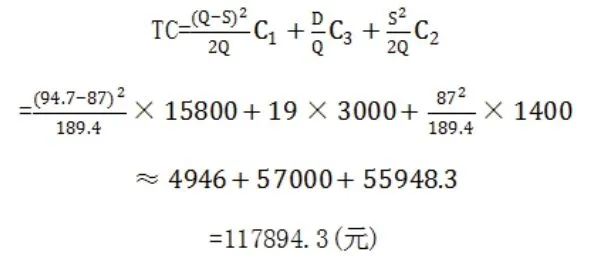
b.订货次数为20次：

求得一年的总费用：

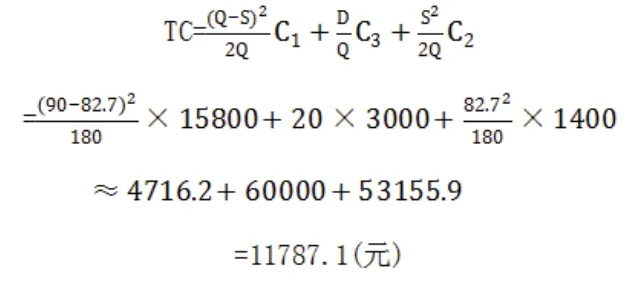
由于117894.3>117872.1，所以每年应订货20次，每次订货90套，最大缺货量为82套。

所需的最少周转资金为：

以上是在没有资金短缺问题的情况下的最优库存策略，如果公司的资金比较紧张，可以根据自身情况适当减少订货量，增加订货次数。

（2）产 品2。有D=R=1000套/年，C1=24500元/套 年，C3=3000元/次，C2=2000元套/年。可求得最优订货批量：

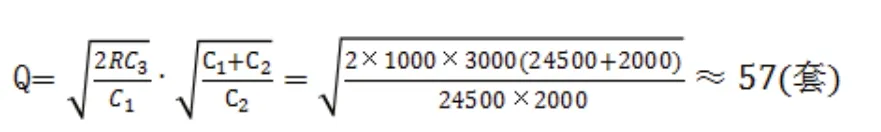
求得最大缺货量：

每年订货次数为：

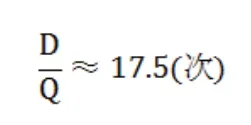
由于非整数，所以分别以17次和18次讨论其总费用，选择最佳次数。

a，订货次数为17次。

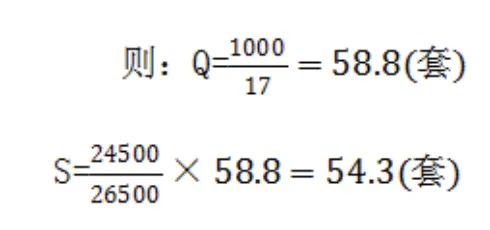
求得一年的总费用：

b.订货次数为18次

求得一年的总费用：

由于105403.8>10536.3，所以每年应订货17次，每次订货59套，最大缺货量为54套[4]。

矿产经济需要对矿物资源进行详细的勘查，并且根据资源的形态进行合理的开采。当矿业资源出现问题时，需要考虑一定的变量约束。系列运用运筹学方法进行处理，依据非线性等动态的管理方法进行调整。通过模型的研究，应该充分证实了工程、环境等因素的条件限制。将经济分析落实到生产运营之中，在投资过程中进行调控，保持良好的生产状态和运筹应用[5]。

运筹学经常性的应用与矿业生产之中，作为计划生产的重要组成部分，实现了很大的经济利益和生产效应。实际生产过程中，运用运筹学方法，提升应用领域的可行性。包括在运输分配矿床等方面都应该使用评价、设备配置以及材料的应用环节。从而实现广泛的线性、非线性的规划与管控。以此，也应该提升多种运筹学的技术引用，无论是在理论文献的收集方面还是在实践生产方面都应该遵从这个标准[6]。

综上所述，用允许的经济订货批量模型（允许缺货模型）来求解，可以获得最优化的订货结果。矿业企业工作过程中，很多的问题都是出现在公式表达和技术的抉择方面。在系统目标确定的情况下，需要考虑到系统的要求，以及参数化的具体处理。无论从生产角度还是运筹学理论分析角度，都应该正是运筹学依据，解决矿业中的实际问题，并且研发新的方法，充分运用计算技术和矿业资源，解决企业管理的问题。