栅前端壁射流抑制二次流的数值研究

赵 树，陈 榴，戴 韧

(上海理工大学 能源与动力工程学院，上海 200093)

在透平叶栅中，端壁二次流带来的流动损失约占总损失的1/3[1]，其中前缘马蹄涡和通道涡[2]均会造成二次流损失。为减少端壁二次流带来的流动损失，多种被动流动控制被应用到透平叶栅中，包括非轴对称端壁[3]、翼刀[4]和前缘壁角[5-7]等，但被动流动控制无法适应不同的工况条件，而射流主动流动控制可以根据需求进行调节。

Aunapu等[8]在优化后的翼刀位置开设12个射流孔，使通道涡远离吸力面。Bloxham等[9]通过在叶栅端壁上开抽吸孔，以吸除端壁上的低动量流体，使通道涡的发展路径向远离吸力面侧的方向发展。Li等[10]将射流应用到压气机端壁上，抑制了吸力面上的流动分离，但也使通道涡得到增强。姜帅[11]和刘华坪等[12]将射流引入到流道端壁，有效改变了通道涡的发展路径，减少了角区分离以及吸力面的流动分离。

除了在流道端壁上开设射流孔外，也有研究人员将射流孔开设在叶片上。Benton等[13-14]在透平叶栅吸力面侧开设射流孔，使涡系远离吸力面，进而降低了总压损失。Mcauliffe等[15]将射流孔布置在吸力面侧，证明低雷诺数下射流有助于抑制吸力面的流动分离，显著降低流动损失。

研究表明，应用射流控制二次流是有效的，但射流位置均处在叶栅内和涡系发展路径上，而二次流的生成是由于边界层的低动量流体到达叶栅前缘位置进而造成滞止分离，因此更优的选择是将射流孔开设在二次流的生成源头。此外，关于射流孔位置、倾斜角、俯仰角和动量系数对二次流的影响规律也不明确。

因此，笔者将射流孔布置在端壁前缘马蹄涡生成的位置，通过分析射流孔参数对前缘马蹄涡的影响，试图从二次流的源头出发来削弱马蹄涡的强度，进而改善后续通道涡的强度，减少流动损失。

1 模型与网格

以Langston[16]平面叶栅为研究对象，其数据见表1。

表1 透平叶栅叶型参数

采用定常雷诺时均方程(RANS)对Langston原始模型和射流模型进行数值计算。湍流模型采用剪切应力输运模型。为了保持数值模型与实验工况的一致性，叶片域上游存在1.45倍轴向弦长的进口域；叶片域中叶片上游和下游均存在0.2倍轴向弦长的流道长度；在叶片域下游存在1.3倍轴向弦长的出口域。参考文献[16]，实验工况如表2所示。

表2 叶栅入口实验工况

无量纲边界层进口速度U为：

(1)

式中：U0为进口速度，取值为33.5 m/s；H为展向叶高，m；z为无量纲展向叶高。

图1为叶栅域网格的拓扑结构示意图。叶栅周围采用O型网格，总层数为29层，第1层网格厚度为0.01 mm，网格厚度增长率为1.2；其他网格采用H型网格，轴向节点数为158，周向节点数为130，径向节点数为80。

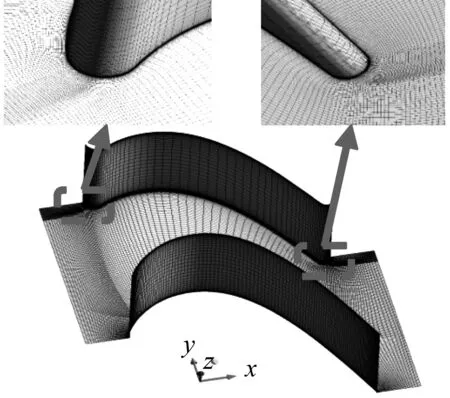
图1 网格示意图

为达到网格无关性的要求，采用不同网格数进行网格无关性验证，结果如表3所示。最终确定网格数为3.28×106。在近端壁位置进行网格加密，第1层网格厚度为0.01 mm，近端壁最大y+为2.289，满足计算要求。计算结果表明，沿x、y和z3个方向的速度残差均小于10-4，在600次的迭代过程中平均总压变化率小于0.5%，说明计算结果收敛。

表3 网格无关性验证

静压系数Cp为：

(2)

式中：ps,local为当地静压；ps,in为进口静压；pt,in为进口总压。

图2为50%叶高处静压系数Cp分布，其中Cax为轴向弦长的绝对长度,x为轴向坐标。从图2可以看出，静压系数模拟值与实验值基本一致，保证了数值模拟的准确性。

图2 50%叶高处静压系数分布

2 射流孔设计

图3给出了射流孔示意图。射流孔主要参数包括射流孔位置、倾斜角α、俯仰角β以及动量系数。

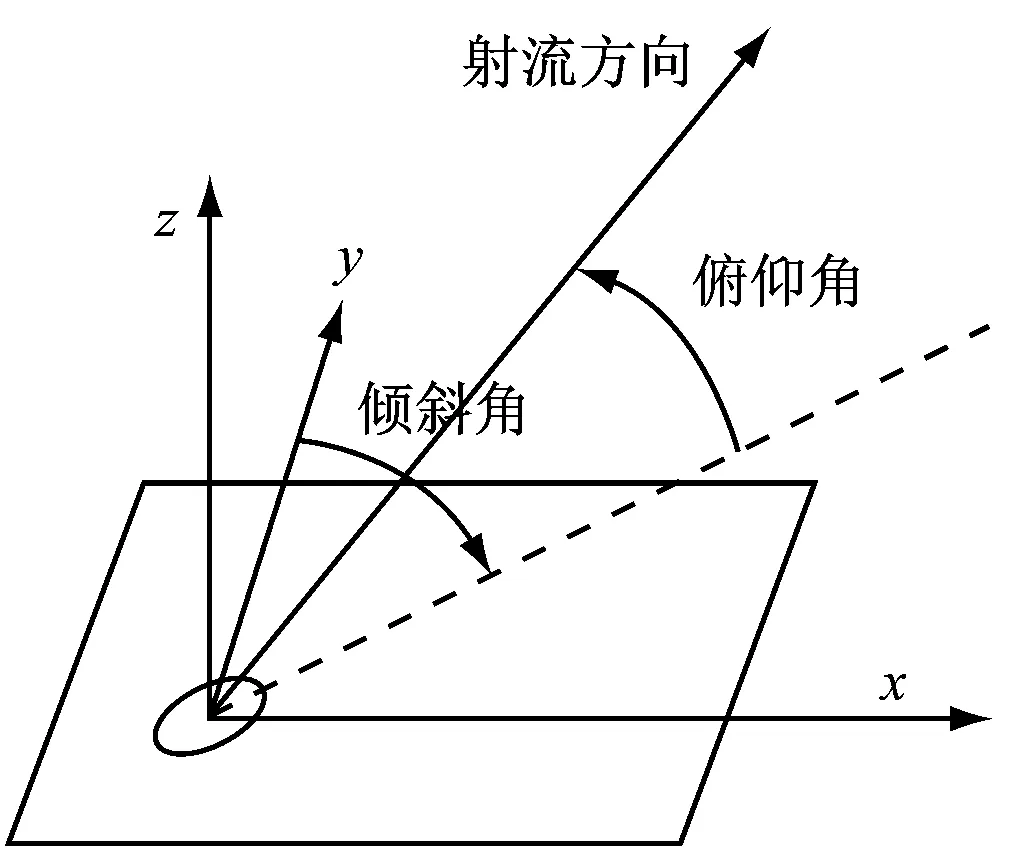
由于仅在下端壁开设射流孔，单个射流孔的动量系数定义为单个射流孔引入动量与主流动量的一半之比。

单个射流孔的动量系数Cμ为：

(3)

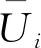
通过引入射流质量流量加权的总压损失系数来判断流动损失。

(4)

(5)

(6)

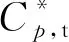
2.1 射流孔位置

在透平叶栅端壁前缘位置开射流孔，其目的是通过引入射流抑制前缘马蹄涡的流动分离，进而降低前缘马蹄涡的强度。图4给出了Langston叶栅原型近端壁的极限流线，line 1、line 2和line 3为对应叶栅前缘法平面与端壁的交线。

图4 Langston叶栅近端壁的极限流线

图5给出了line 1、line 2和line 3的Cf,x分布，其中Cf,x表示无量纲的壁面剪应力Cf在x轴方向的分量。

Cf可表示为：

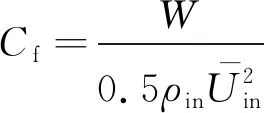
(7)

式中：W为壁面剪应力。

Cf,x为正说明主流沿x轴正向流动，为负则沿x轴反向流动。结合图4和图5可知，Cf,x的正负与极限流线方向一致，因此图4中点1、2、3与图5中的3个点对应，其中点2为前缘马蹄涡的流动分离点。

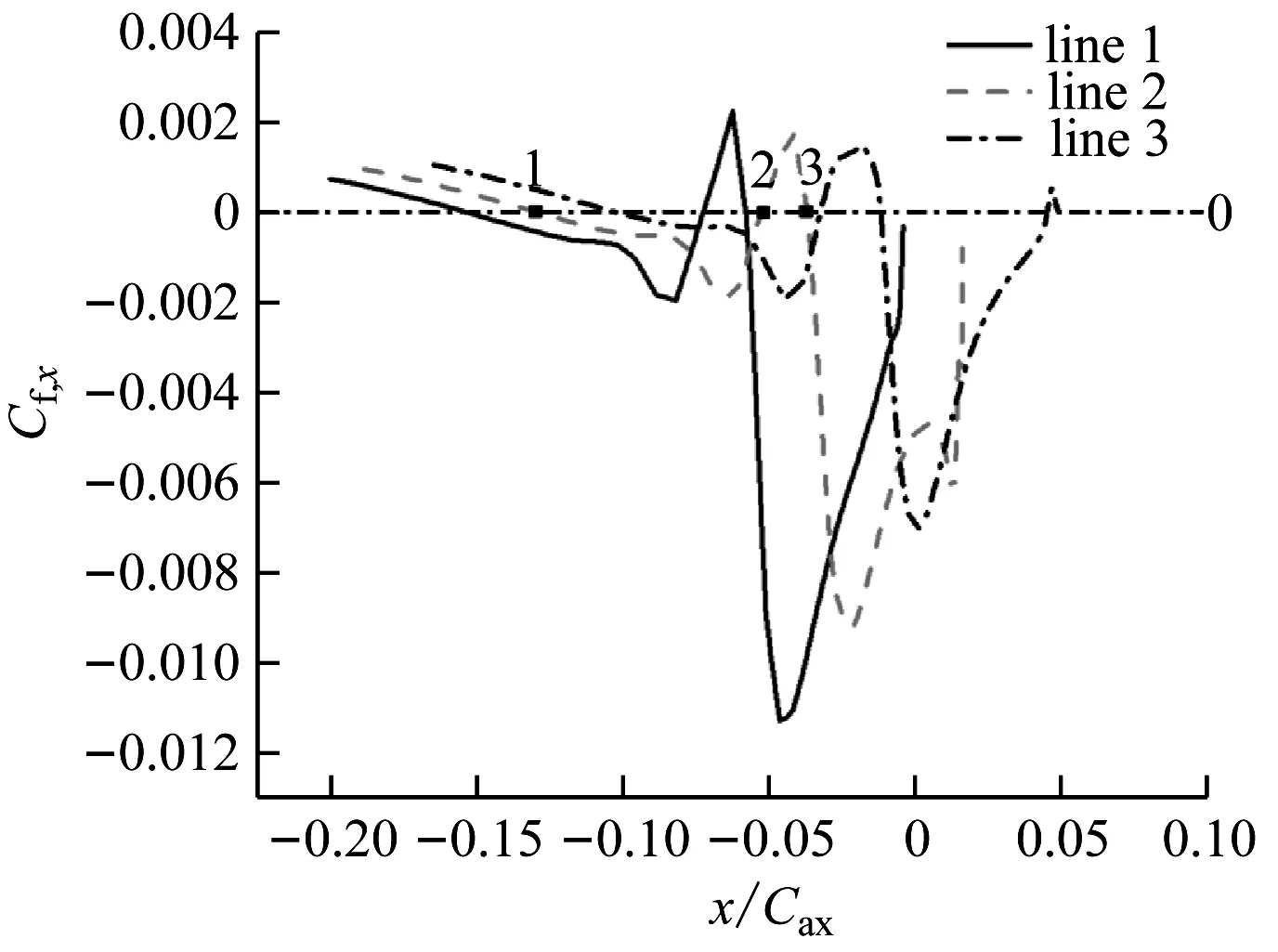
图5 3条交线沿轴向弦长的Cf,x分布

为控制前缘马蹄涡的流动分离，只需将射流孔的位置布置在流动分离线上。采用3个射流孔，分别布置在与line 1、line 2和line 3对应的流动分离点上。

2.2 射流孔俯仰角β和动量系数Cμ

由于前缘马蹄涡为三维流动分离，设置射流孔倾斜角α不变，角度方向与射流孔所在位置的近端壁极限流线方向一致。

为分析射流孔俯仰角β和动量系数Cμ对前缘马蹄涡的影响，对这2个因素进行全因子组合分析。参照文献[13]，单个射流孔动量系数分别取为0.02%、0.05%、0.1%、0.2%和0.3%，射流孔俯仰角β取值为20°、30°、40°和50°。图6给出了x/Cax=0.9截面下不同参数的射流模型和Langston原始模型总压损失系数比的分布。由图6可知，在射流孔俯仰角为20°～50°内，随着β的增大，总压损失系数比呈先减小后增大的趋势；随着动量系数由0.02%增大到0.3%，总压损失系数比呈先减小后增大的趋势。

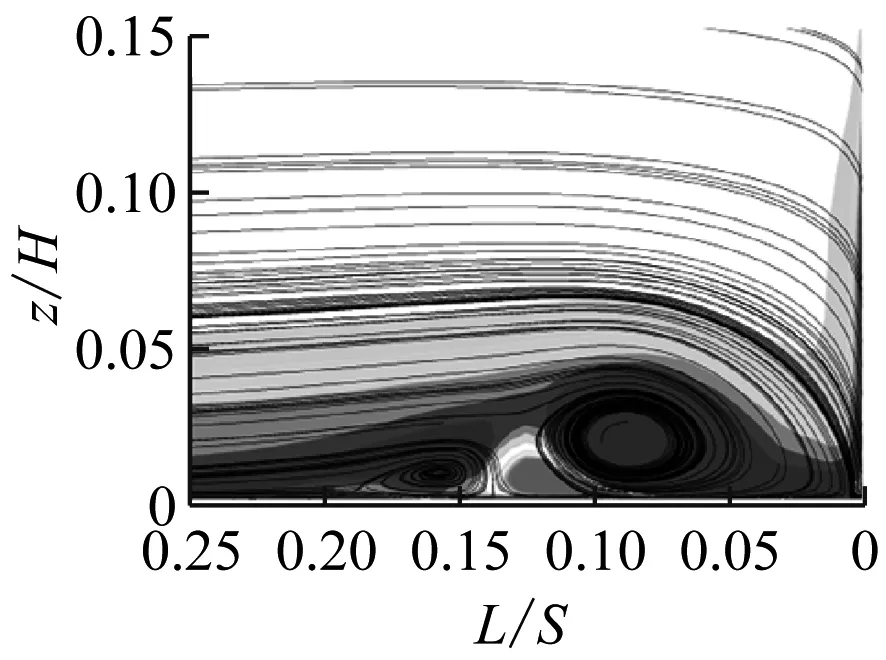
图7给出了动量系数为0.10%时不同射流孔俯仰角下叶栅前缘法平面的流线及涡量图。其中，L为法平面到叶栅前缘位置的距离。

涡量Ωx为：

(8)

式中：v、w分别为y和z方向的速度分量。

由图7可知，将射流孔布置在流动分离点时，不同射流孔俯仰角均可抑制前缘马蹄涡的流动分离，其主要差别在于其大小会影响前缘马蹄涡的大小形态。随着β从30°增大至50°，马蹄涡变大，同时引入射流的径向速度w也增大。由于径向速度与主流速度互相垂直，因此随着射流孔俯仰角的增大，射流对主流的干扰程度也越大，造成前缘马蹄涡的湍动能增大(见图8)，流动损失也增大。由图7(b)可知，由于射流孔俯仰角过小，引入的射流会压缩前缘马蹄涡，因此也会造成前缘马蹄涡湍动能增大。因此，随着β从20°增大至50°，总压损失系数比呈先减小后增大的趋势，见图6。

图6 射流孔俯仰角和动量系数对总压损失系数比的影响

(a) Langston原始模型

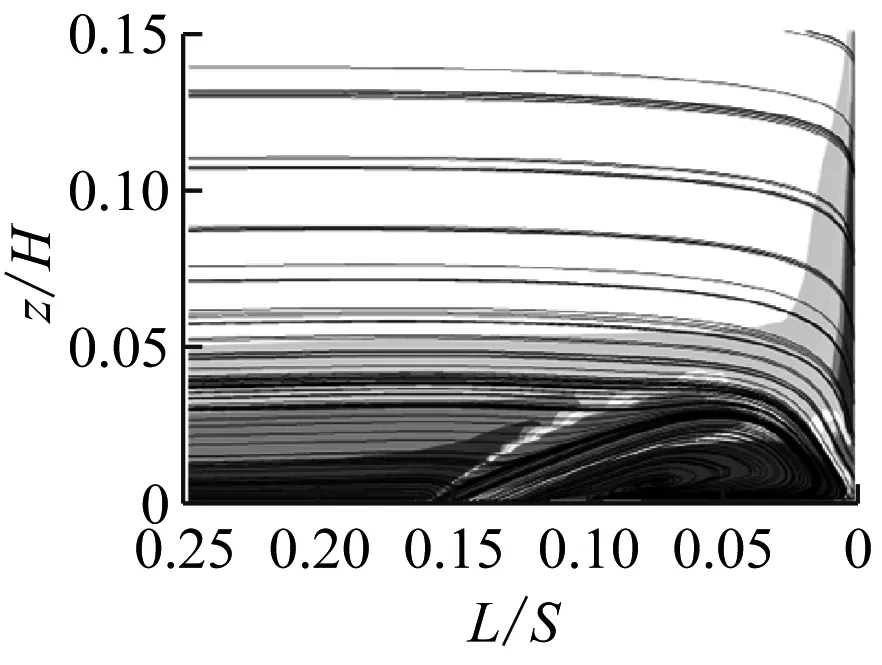
(b) β=20°

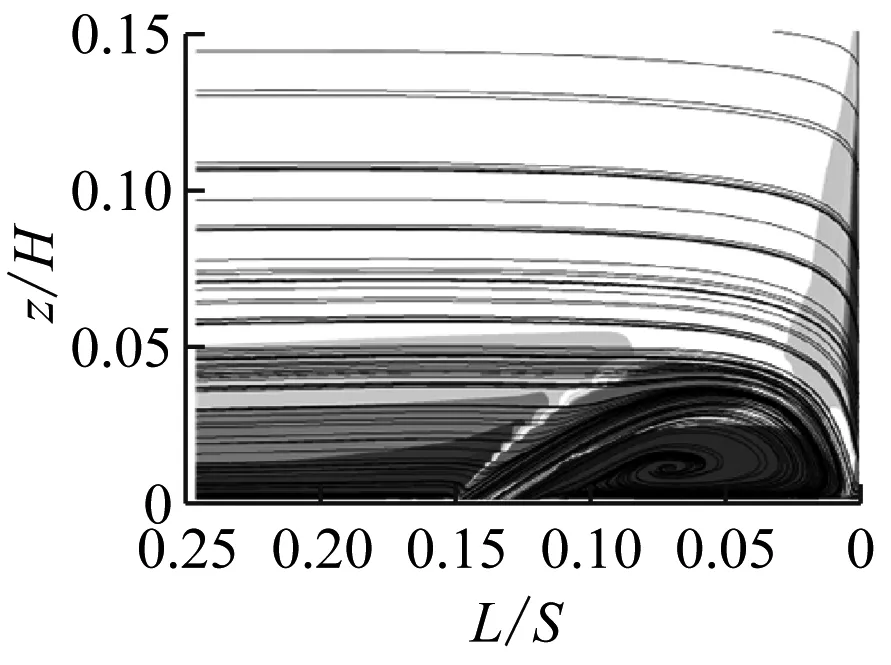
(c) β=30°

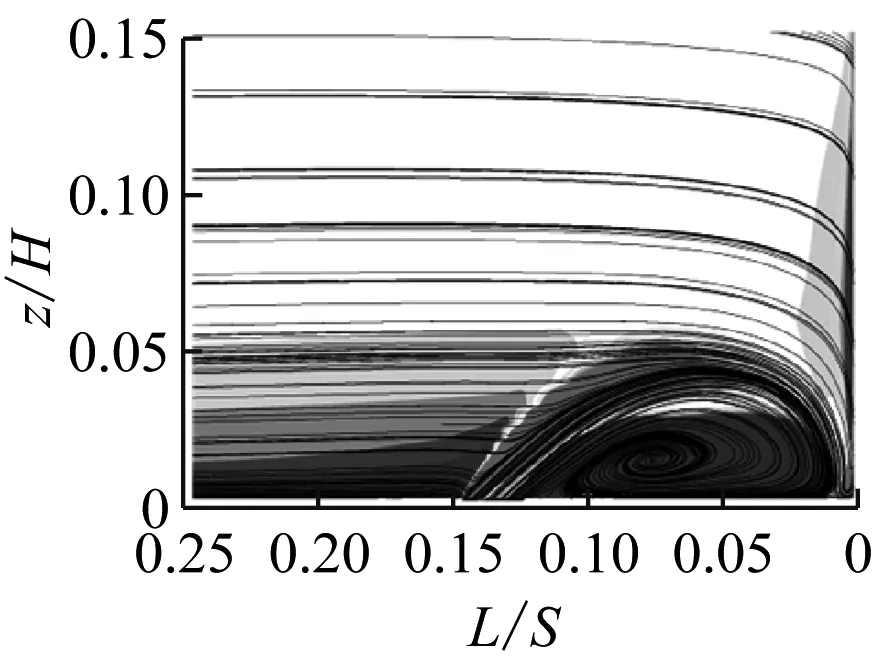
(d) β=40°

(e) β=50°

图9给出了射流孔俯仰角为30°时不同动量系数下的涡量图，相应的湍动能见图10。由图9可知，随着动量系数从0.02%增加到0.1%，前缘马蹄涡的流动分离得到了抑制，但随着动量系数的增大，射流会撞击叶栅前缘，从而造成更大的流动损失。从图10可以看出，湍动能与涡量的变化趋势相对应。

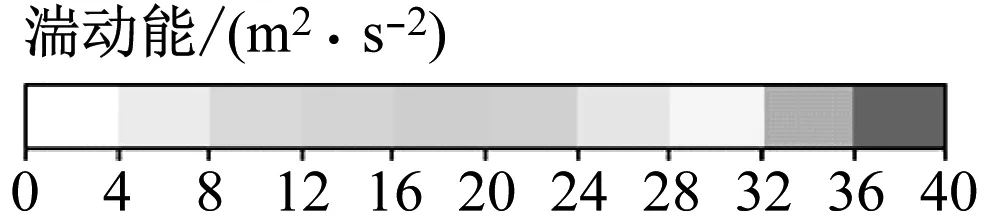
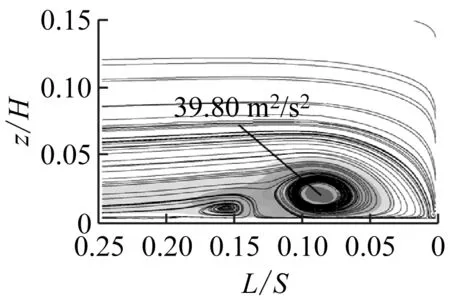
(a) Langston原始模型

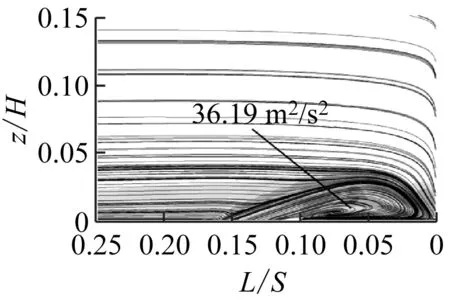
(b) β=20°

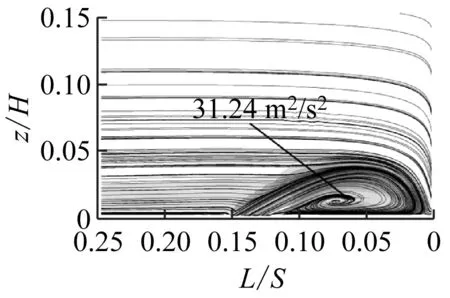
(c) β=30°

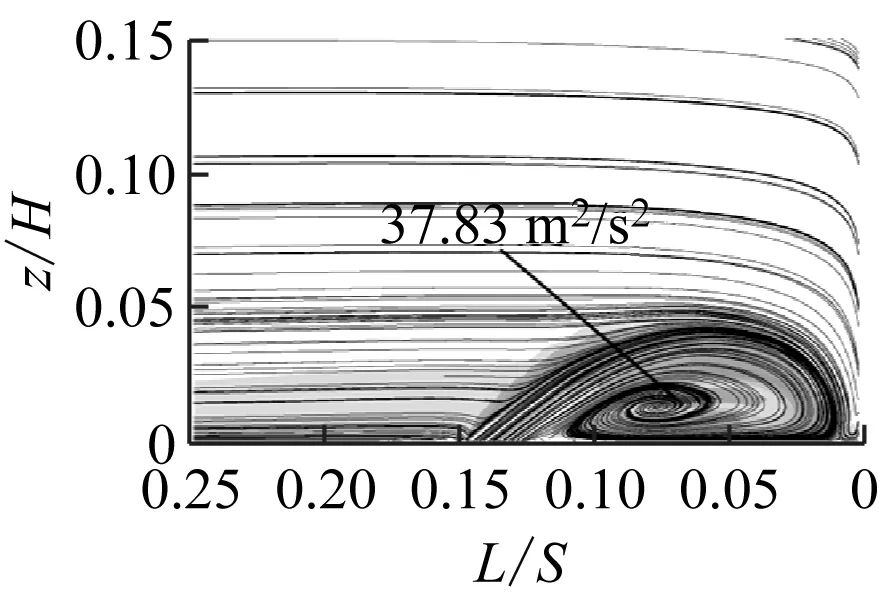
(d) β=40°

(e) β=50°

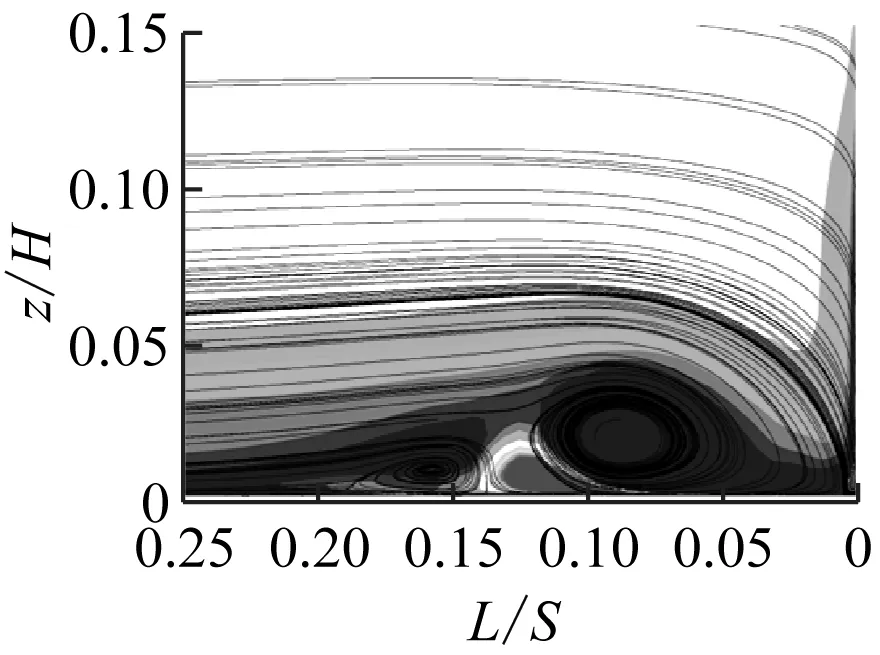
(a) Langston原始模型

(b) Cμ=0.02%

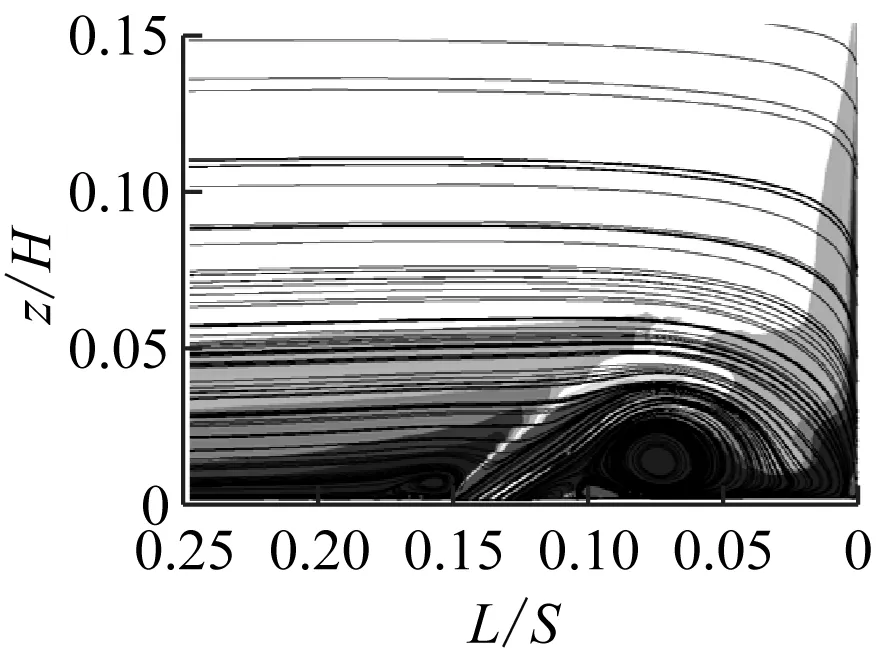
(c) Cμ=0.05%

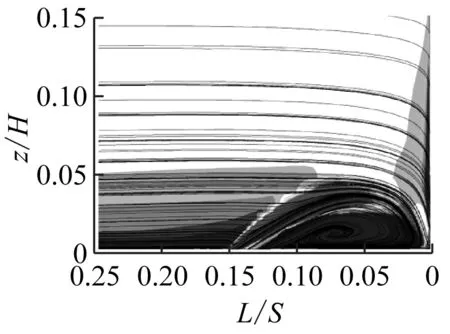
(d) Cμ=0.10%

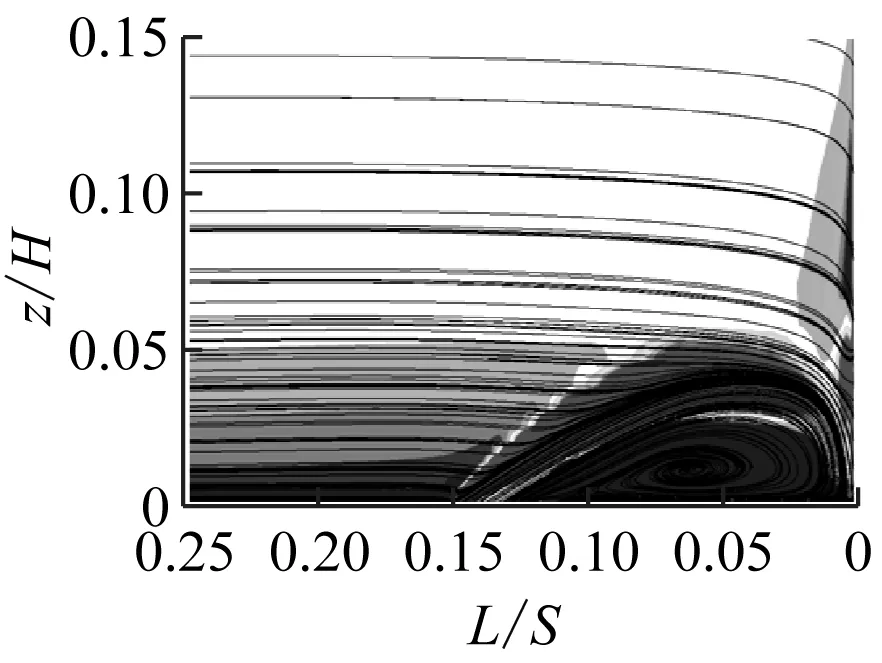
(e) Cμ=0.20%

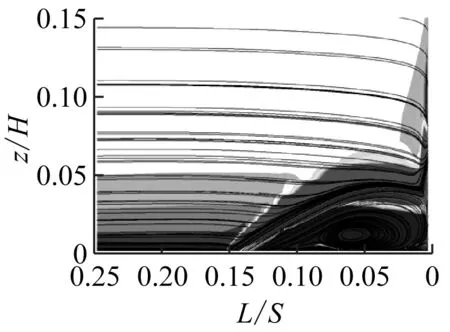
(f) Cμ=0.30%

(a) Langston原始模型

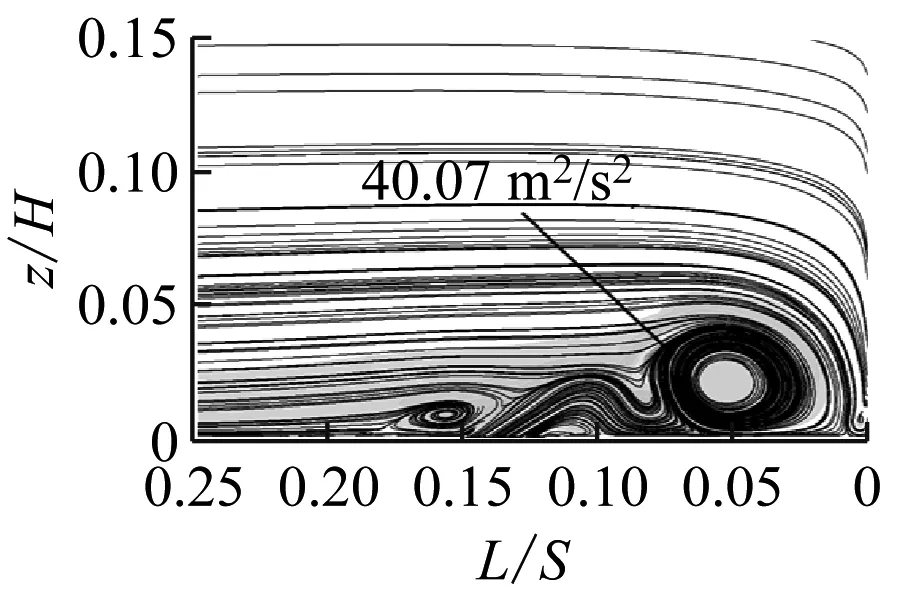
(b) Cμ=0.02%

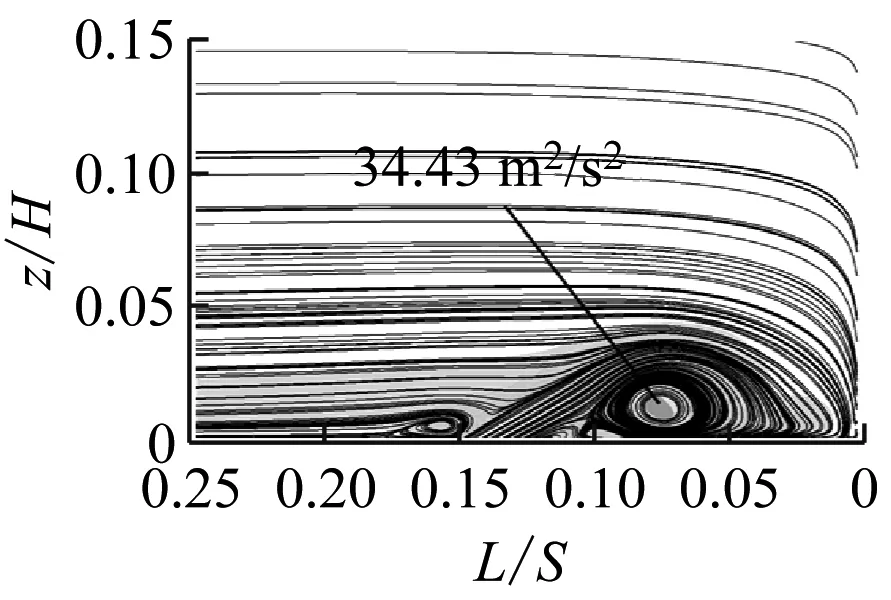
(c) Cμ=0.05%

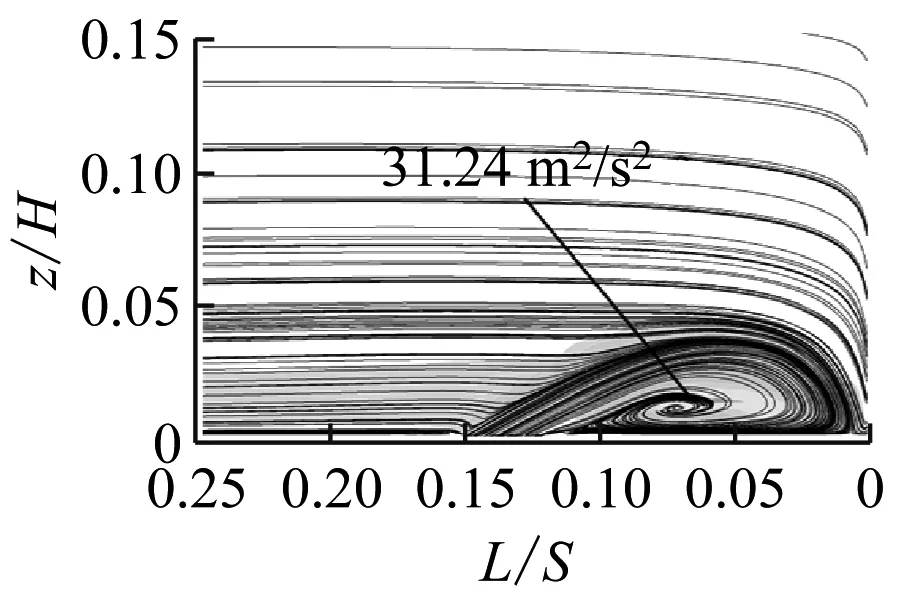
(d) Cμ=0.10%

(e) Cμ=0.20%

(f) Cμ=0.30%

因此，在动量系数为0.02%～0.3%内，随着动量系数的增大，总压损失系数比呈先减小后增大的趋势，也符合图6中总压损失系数比的变化规律。由图6可知，总压损失系数比大于1主要集中在动量系数过小的情况下。动量系数过小，则说明前缘马蹄涡的流动分离没有得到抑制，从而也说明在减少端壁二次流引起的流动损失的措施中，对前缘马蹄涡流动分离现象进行控制更为重要。当射流孔俯仰角为40°、动量系数为0.1%时，总压损失系数比达到最小，因此选择上述取值对流动结果进行分析。

3 射流对叶栅流动性能的影响

3.1 射流对叶栅通道涡发展过程的影响

图11为Langston原始模型和射流模型(β=40°、Cμ=0.1%)前缘法平面的湍动能图。对比Langston原始模型和射流模型的流动情况可知，引入的射流抑制了前缘马蹄涡的流动分离，同时使前缘马蹄涡的湍动能由39.87 m2/s2减小到38.19 m2/s2，且整体湍动能得到削弱。其原因是引入的射流改变了叶栅近端壁的低动量流体，抑制了流动分离，且流体达到叶栅前缘位置时径向压力梯度得到改善，进而改善了前缘马蹄涡湍动能。

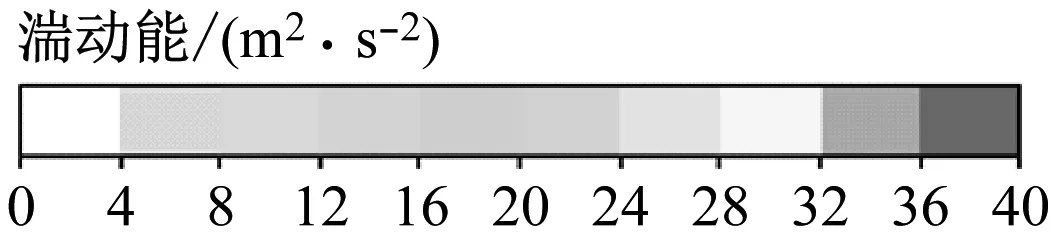
(a) Langston原始模型

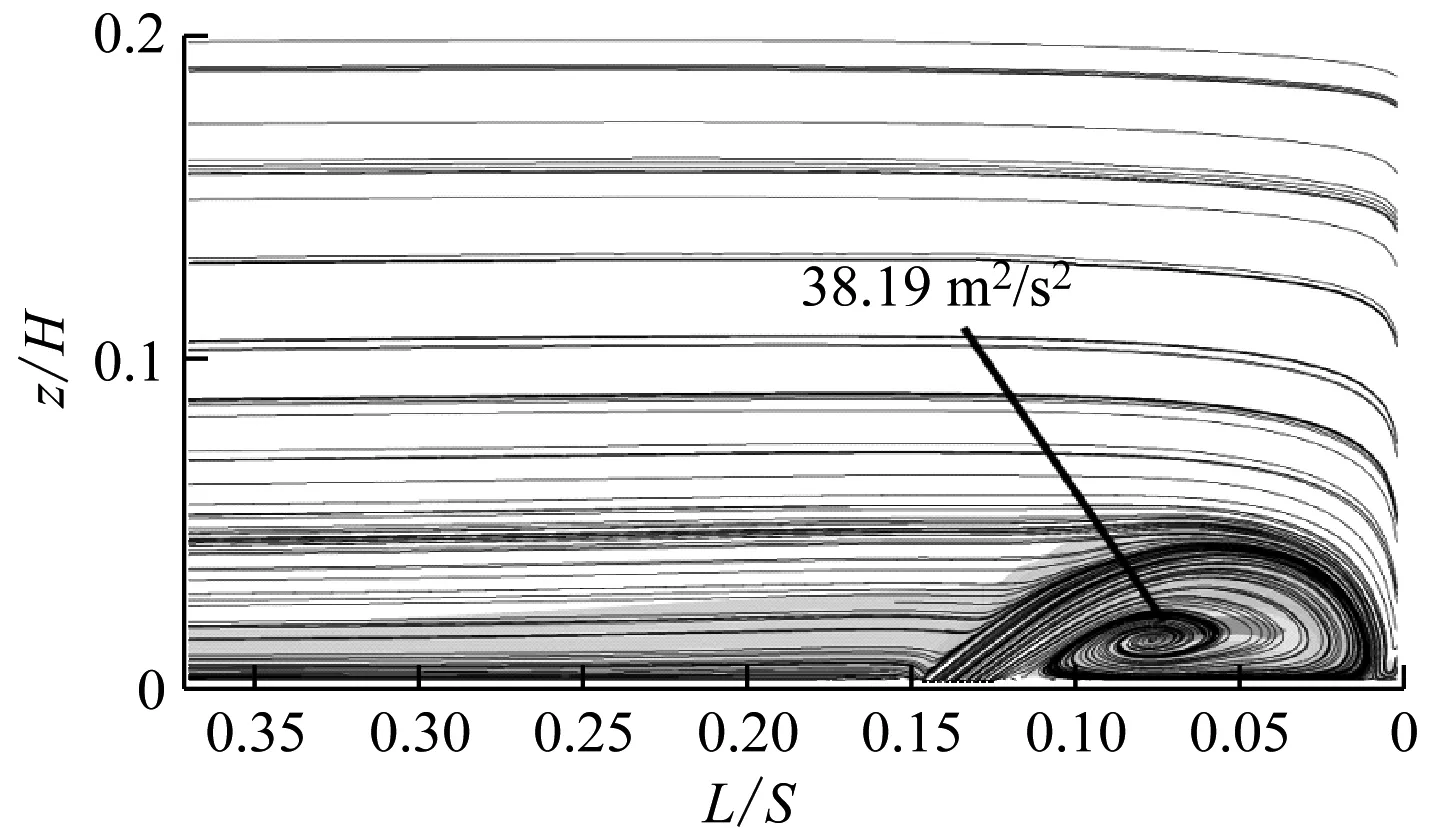
(b) 射流模型

图12为射流模型与Langston原始模型流向湍动能的差值图，差值为负表示该位置湍动能被削弱。对比不同模型的湍动能在流道发展的过程可以看出，引入的射流削弱了前缘马蹄涡，从而使流向湍动能减小。

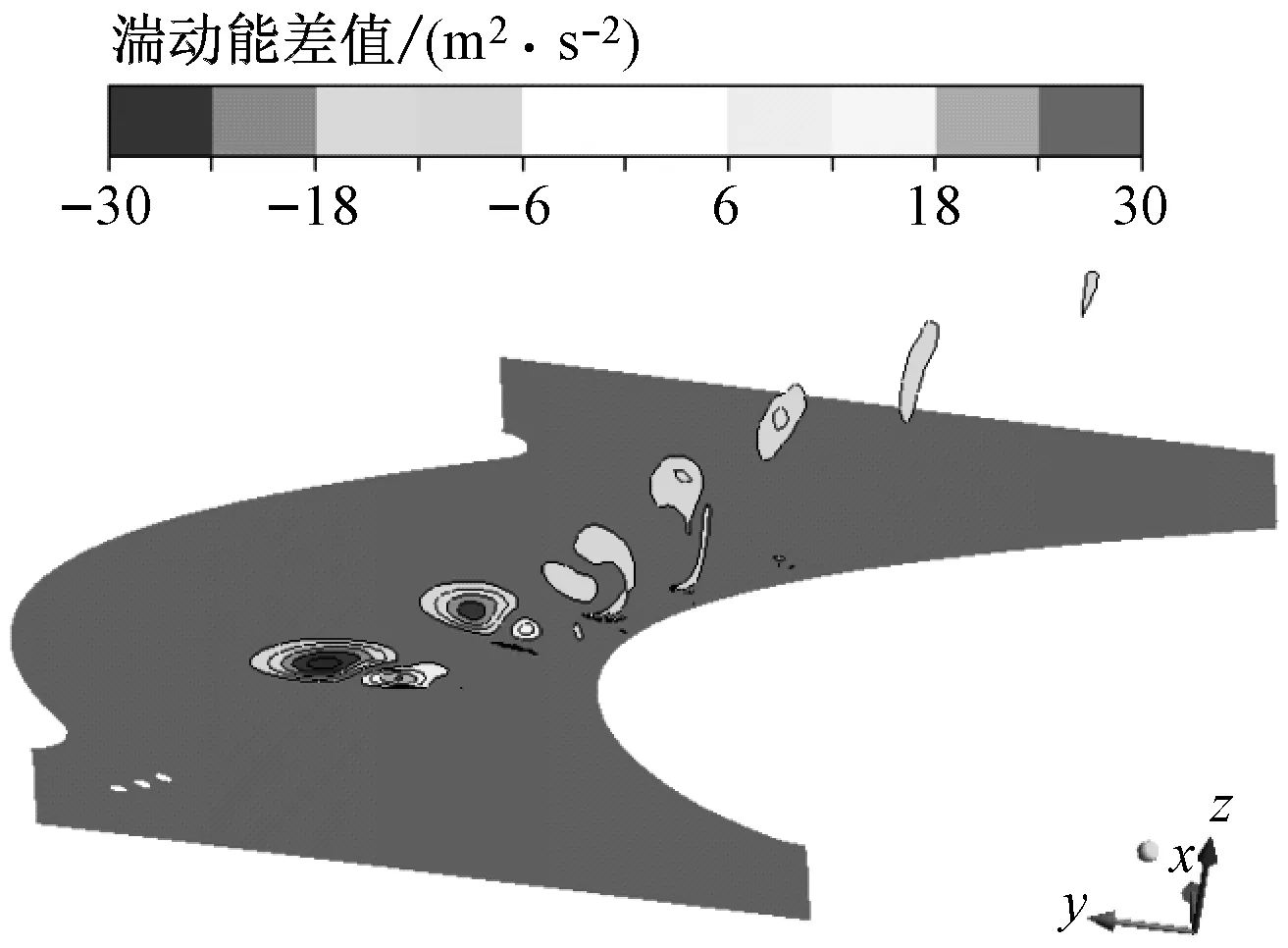
图12 射流模型和Langston原始模型流向湍动能差值图

图13给出了沿流向总压损失系数的变化曲线。从图13可以看出，引入的射流有效减小了流道内的总压损失系数，在x/Cax=0.9截面总压损失系数可降低约8.83%。虽然Langston原始模型和射流模型的总压损失系数大小有差异，但整体趋势不变，说明射流没有影响流道中整体流动结构，但有效改善了流动特性。

图13 Langston原始模型和射流模型沿流向总压损失系数的分布

3.2 射流对叶栅近出口流场的影响

从图14可以看出，相对展向叶高为0.2～0.5时，引入射流可有效减小总压损失系数，该展向叶高范围与通道涡的位置对应，因此也使射流通道涡的湍动能得到削弱。

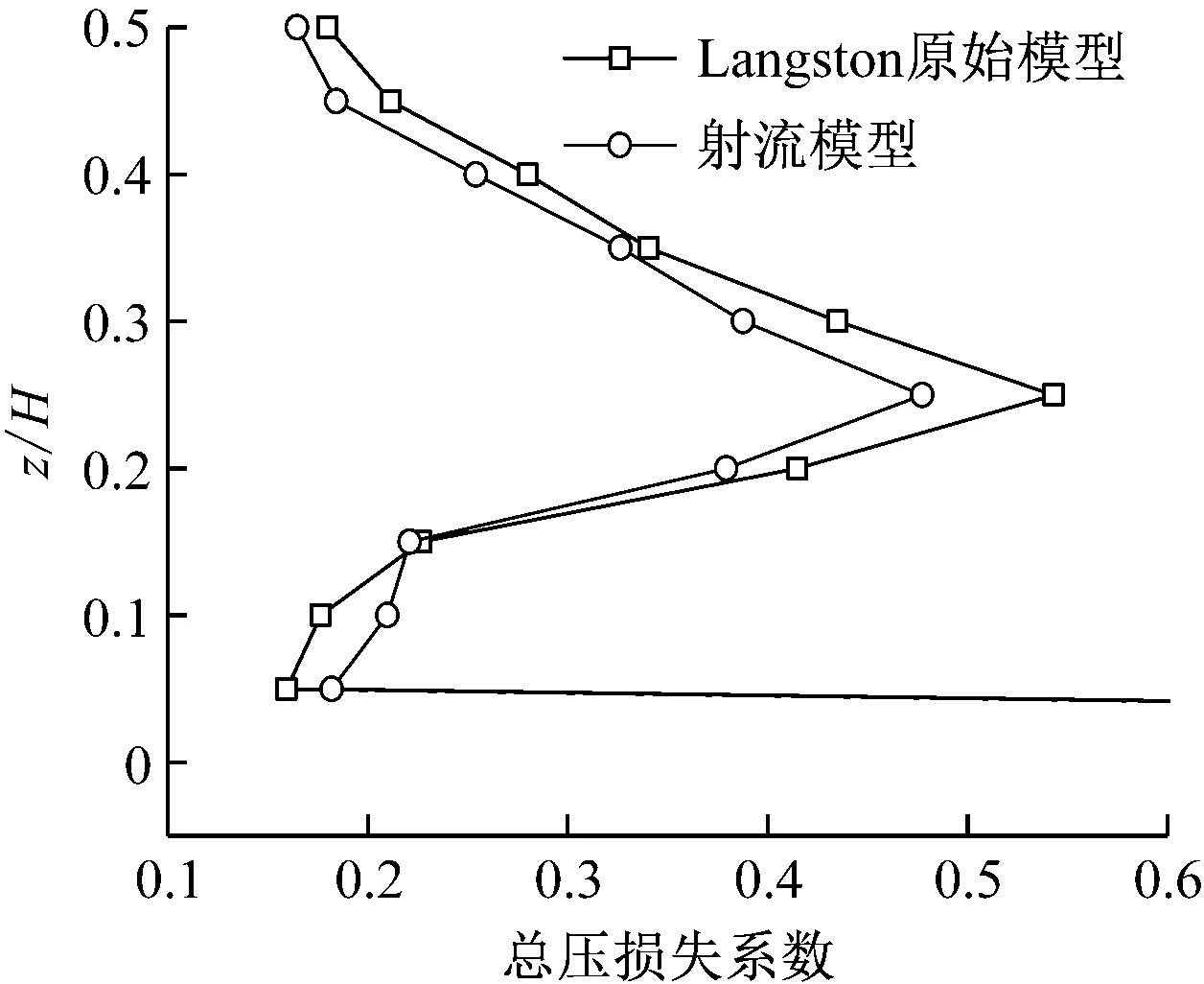
图14 x/Cax=0.9截面处总压损失系数沿相对展向叶高的分布

4 结 论

(1) 射流孔俯仰角β小于20°时，射流会对前缘马蹄涡产生挤压作用，不利于削弱其湍动能；随着俯仰角β的增大，射流的径向速度分量增大，当俯仰角超过40°时，其对主流的干扰也更明显，会造成额外的流动损失。

(2) 单个射流孔动量系数小于0.05%时，射流能量不足以吹动近端壁的低动量流体；当动量系数超过0.1%时，射流开始撞击到前缘叶片，增加了额外的流动损失。

(3) 射流孔倾斜角α的方向应与射流孔所在位置近端壁极限流线方向一致。β=40°、Cμ=0.1%时，可从涡系的源头抑制前缘马蹄涡的流动分离，并削弱其湍动能，涡系的湍动能也变弱，流向总压损失系数相应减少，叶栅近出口总压损失系数可降低8.83%。