基于SSWPT的转子油膜失稳故障分析

唐贵基，徐振丽

(华北电力大学 河北省电力机械装备健康维护与失效预防重点实验室，河北保定 071003)

滑动轴承作为旋转机械的关键部件，因其能够有效增强转子系统的支撑能力而被广泛使用[1]。当转子受到外界因素的干扰时，轴承的油膜力与负载不平衡，使轴颈围绕平衡位置旋转，从而产生油膜涡动和油膜振荡[2]。一旦转子系统发生油膜振荡，会严重损坏转子，影响整个机械系统的正常运行，因此研究转子系统油膜失稳故障对确保转子正常安全运行具有重要意义。实际工况下的转子故障信号通常是非线性、非平稳的多分量信号，它们的频率成分随着时间变化。时频分析方法是处理非平稳信号的有效工具，被广泛用于转子故障诊断中[3-4]。目前，常用的时频分析方法有短时傅里叶变换[5](Short-time Fourier Transform,STFT)、小波变换[6](Wavelet Transform，WT)、Wigner-Ville分布以及希尔伯特黄变换[7](Hilbert-Huang Transform，HHT)等。但是上述时频分析方法存在一定的不足:STFT由于受时频窗的影响，其高频和低频信号的分辨率不能同时兼顾；小波变换的时频图存在能量扩散现象，使得频率分辨率较低；Wigner-Ville分布由于受交叉项的干扰，限制了该方法的应用。HHT是美国华裔科学家Huang N E在1998年提出的一种时频分析方法，主要包括经验模态分解(Empirical Mode Decomposition，EMD)和希尔伯特变换两部分。HHT方法具有良好的自适应性，已被广泛应用于旋转机械的故障诊断中[8-9]。然而，EMD方法存在模态混叠、端点效应等问题，严重影响了时频分析的精度，对故障特征诊断造成了干扰。针对EMD方法的不足，近年来一些学者提出了变分模态分解(Variational Modal Decomposition，VMD)及经验小波变换(Empirical Wavelet Transform，EWT)等分解方法,可用于旋转机械故障诊断中，取得了丰硕的成果[10-12]。但是，VMD方法需要人为设定分解层数及惩罚因子，EWT方法对参数的选取较复杂，若参数设置不当将导致故障特征提取不准确。因此，上述时频分析方法难以提取转子在实际运行工况下的故障特征。

同步压缩变换(Synchrosqueezing Transform，SST)是Daubechies等[13]提出的一种先进的时频后处理技术，本质是时频重排与连续小波变换的结合，将小波变换得到的时间-尺度系数重新分配压缩至时间-频率轴上。SST对于非平稳信号具有较高的频率分辨率，是故障诊断领域的一个研究热点，目前已成功应用到轴承故障诊断[14]。同步压缩小波包变换[15](Synchrosqueezed Wave Packet Transform，SSWPT)是最近发展起来的一种新的时频分析方法，该方法是SST与小波包变换的结合，能够准确提取信号的瞬时信息，比SST具有更高的时频分辨率及更好的抗噪性能。目前，该方法在医学信号分析方面取得了一定的成果。笔者将同步压缩小波包变换引进到转子油膜失稳故障分析中，提出了一种基于SSWPT的转子油膜失稳故障分析方法，在仿真信号、实验信号以及现场数据分析中取得了良好的效果。

1 同步压缩小波包变换原理

给定一个母波包w(ξ),使其满足：

(1)

其中，|ξ|>1，ε>0，m为非负整数。

(2)

式中：a为尺度因子；b为平移因子。

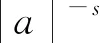
小波包族的傅里叶变换表示为：

(3)

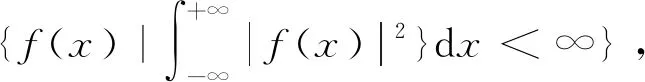
(4)

式中：Wf(a,b)为小波包变换系数；|a|>1,b∈R。

信号通过小波包变换后可以得到小波包变换系数，此时可求取瞬时频率vf(a,b)：

(5)

最后根据计算得到的瞬时频率，建立(b，a)→(b,vf(a,b))的映射关系，将小波包变换系数从时间-尺度平面转化到时间-频率平面，使得信号中各频率成分在频域方向进行压缩，提高了小波包在频域上的分辨率，使信号中各频率分量清晰地显示在时频图上，则同步压缩小波包变换的表达式Tf(v,b)可以表示为：

(6)

其中，δ表示狄拉克函数，Rvf(a,b)表示瞬时频率的实部;v为信号的中心频率。

综上所述，基于同步压缩小波包变换的步骤如下：(1)利用小波包变换求取小波包变换系数Wf(a,b)和主偏导数∂bWf(a,b)；(2)计算瞬时频率vf(a,b)，并进行同步压缩得到Tf(v,b)。

2 仿真信号分析

为验证SSWPT的时频分析能力，现构造如下2组仿真信号x1(t)和x2(t)：

(7)

(8)

式中：x11(t)为调频信号；x12(t)为调幅调频信号；x13(t)为随机噪声；x21(t)、x22(t)为余弦信号；x23(t)为随机噪声；fr1、fr2为转频；f1、f2和f3为中心频率；N1、N2为信号点数；t为时间;randn为随机函数，其中仿真信号的采样频率为1 024 Hz，采样点数为2 048。

仿真信号x1(t)由调频信号x11(t)、调幅调频信号x12(t)和随机噪声x13(t)3个分量叠加而成。其中fr1=2 Hz，f1=50 Hz，f2=100 Hz，f3=5 Hz。仿真信号x2(t)是1个由3个分量构成的随时间变化的非平稳信号，式(8)中包含转频fr2(t)=30+30t和3倍转频的谐波分量3fr2。

x1(t)、x2(t)的时域波形图及频谱图如图1和图2所示,其中f为频率。从图2(a)可以看出，仿真信号x1(t)存在2个调制频带，而2个中心频率不易被识别。由图2(b)可知，仿真信号x2(t)的频谱存在较宽的频带，出现频率涂抹现象。因此，仅依靠频谱分析不能有效提取信号的特征频率。

(a) x1(t)的时域波形图

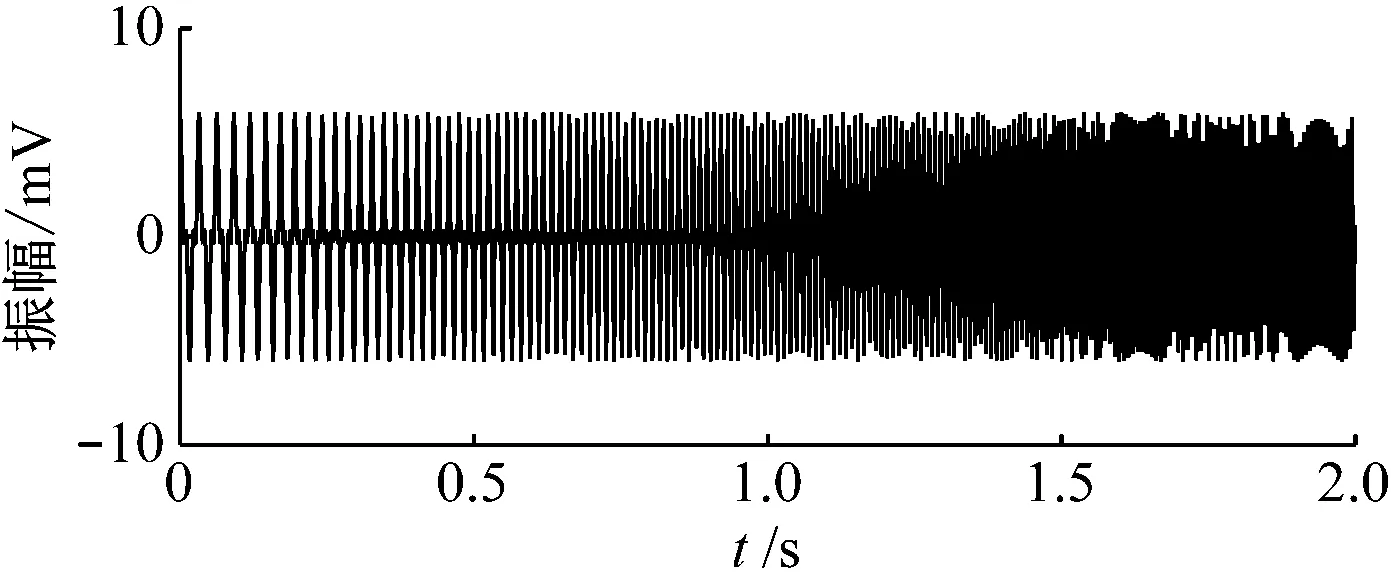
(b) x2(t)的时域波形图

(a) x1(t)的频谱图

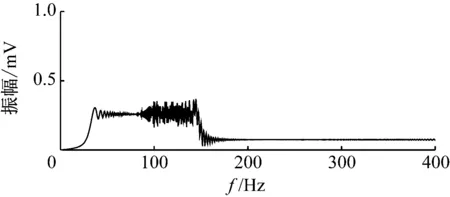
(b) x2(t)的频谱图

分别对仿真信号x1(t)和x2(t)进行同步压缩小波包变换，结果如图3所示。由图3(a)可知，SSWPT方法能够精确地把仿真信号x1(t)的频率成分有效分离。由图3(b)可知，SSWPT方法能够检测到各频率成分随时间的变化趋势。

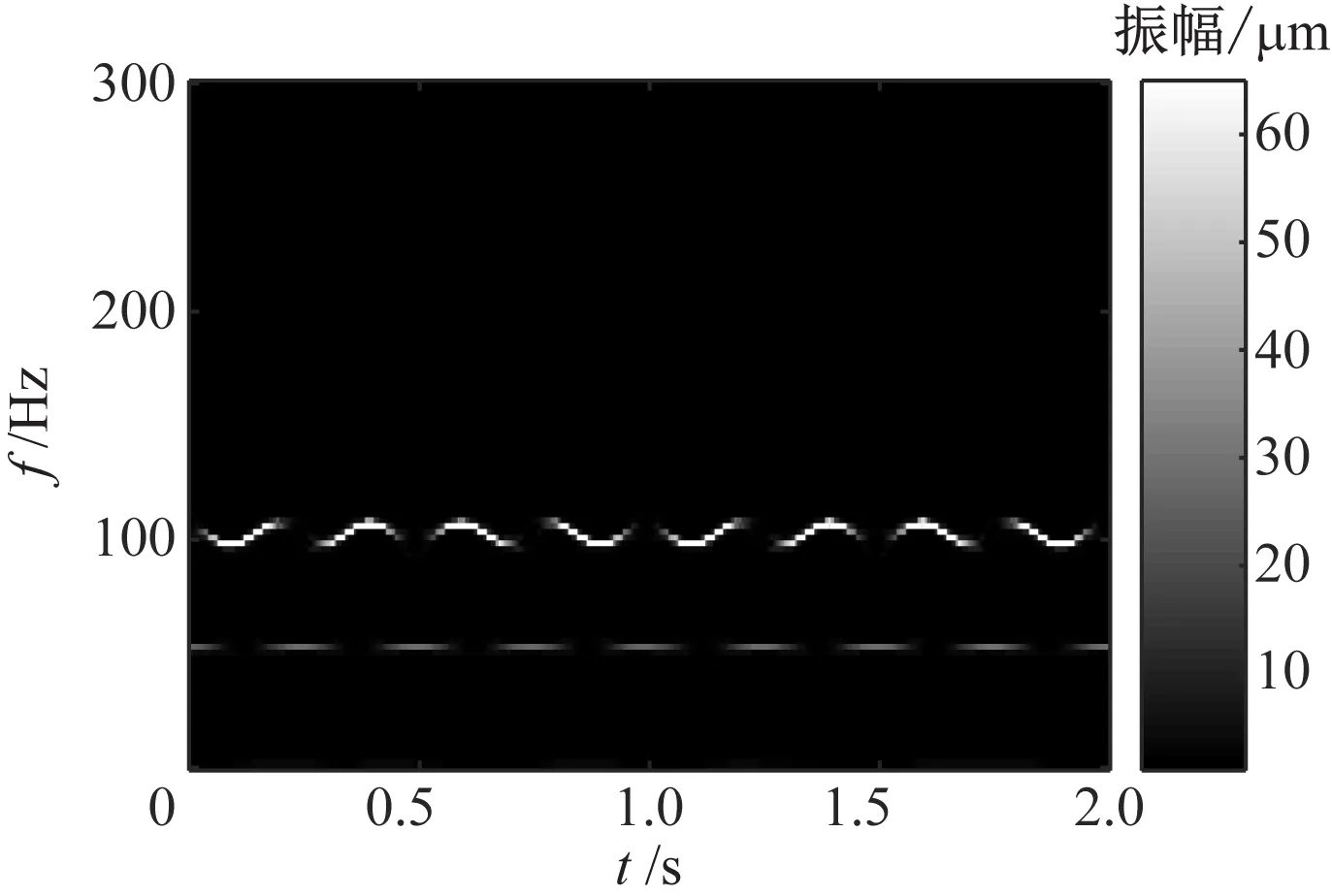
(a) x1(t)的SSWPT时频图

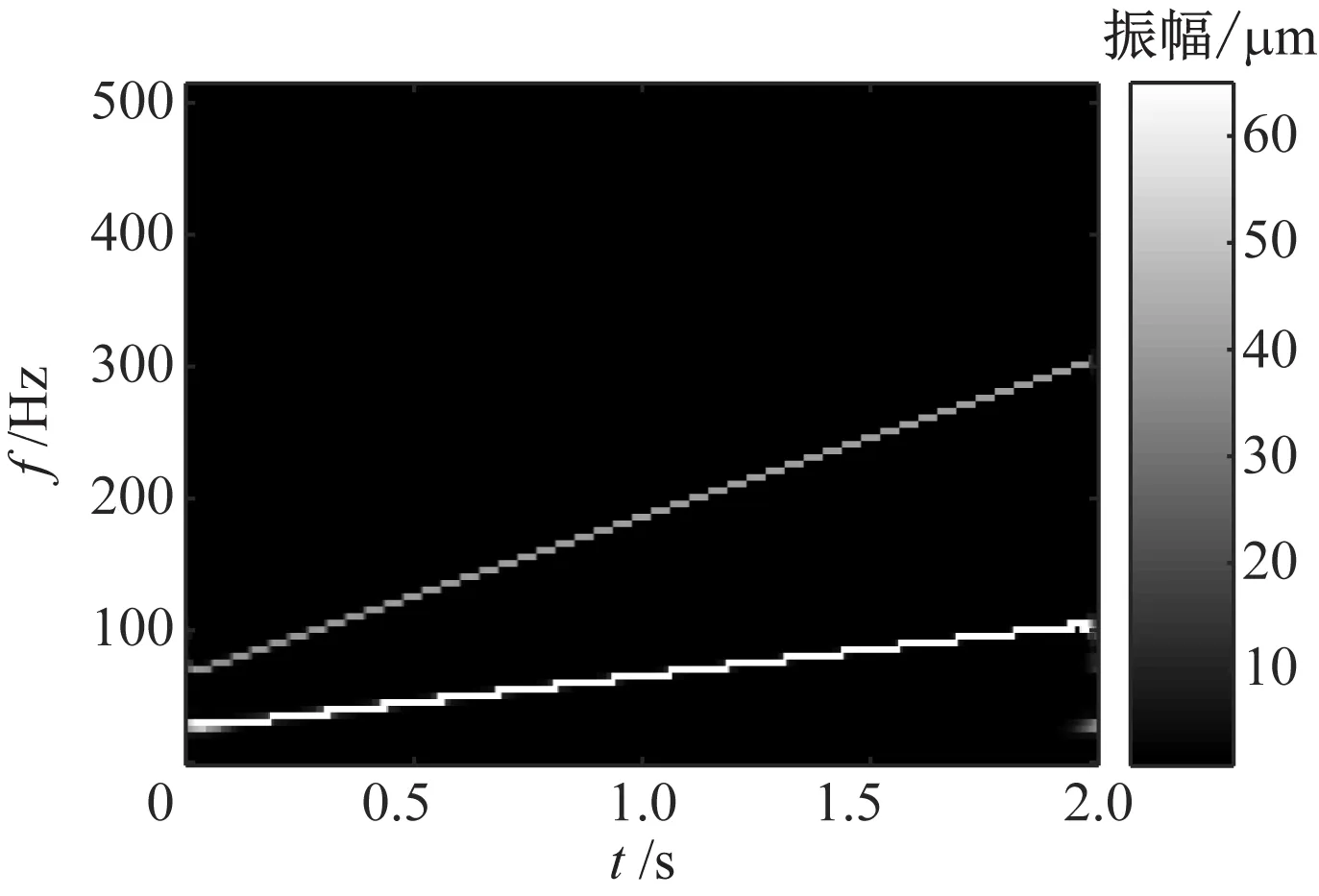
(b) x2(t)的SSWPT时频图

图4(a)和图4(b)分别给出了HHT方法对仿真信号x1(t)和x2(t)的分析结果。由图4(a)可知，HHT方法提取的频率分量之间出现了不同程度的模态混叠现象，不能精确提取信号的频率成分。从图4(b)可以观察到频率分量在高频部分聚集性较低。

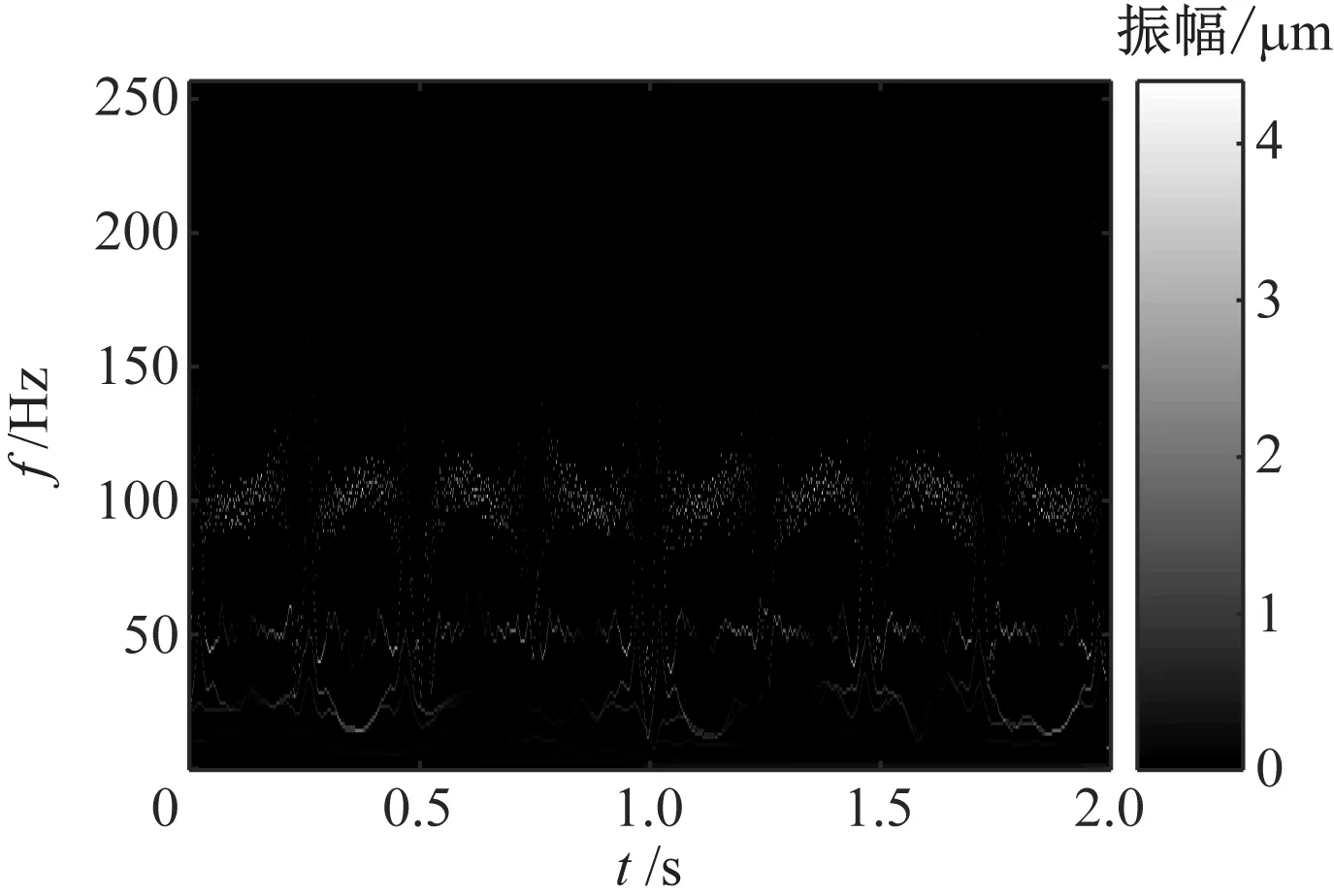
(a) x1(t)的HHT时频图

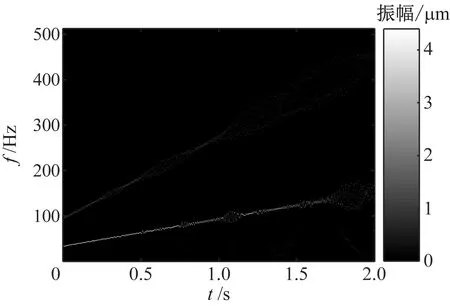
(b) x2(t)的HHT时频图

3 实验分析

实验装置采用图5所示的Bently-RK4转子实验台，分别进行了恒定转速和变转速工况下的油膜失稳故障实验。振动信号通过电涡流传感器采集，信号采样频率为1 280 Hz。

图5 Bently-RK4转子实验台

3.1 恒定转速工况下油膜涡动故障分析

首先将转子升速至实验转速2 800 r/min模拟油膜涡动故障。油膜涡动是转子受到轴承油膜力的作用而产生的涡动，是一种自激振动。当转子系统处于油膜涡动状态时，其振动信号中含有基频及油膜涡动频率，由于涡动频率与基频的二分频接近，油膜涡动又称为半频涡动。转子油膜涡动信号的时域波形及频谱如图6所示。由图6可知，转子油膜涡动的时域波形发生变形。在频谱图中，二分频振幅fo较为突出，且图中出现了振幅较低的高次谐波成分。因此，仅根据频谱分析不能有效诊断转子是否发生了油膜涡动故障。

(a) 油膜涡动信号的时域波形图

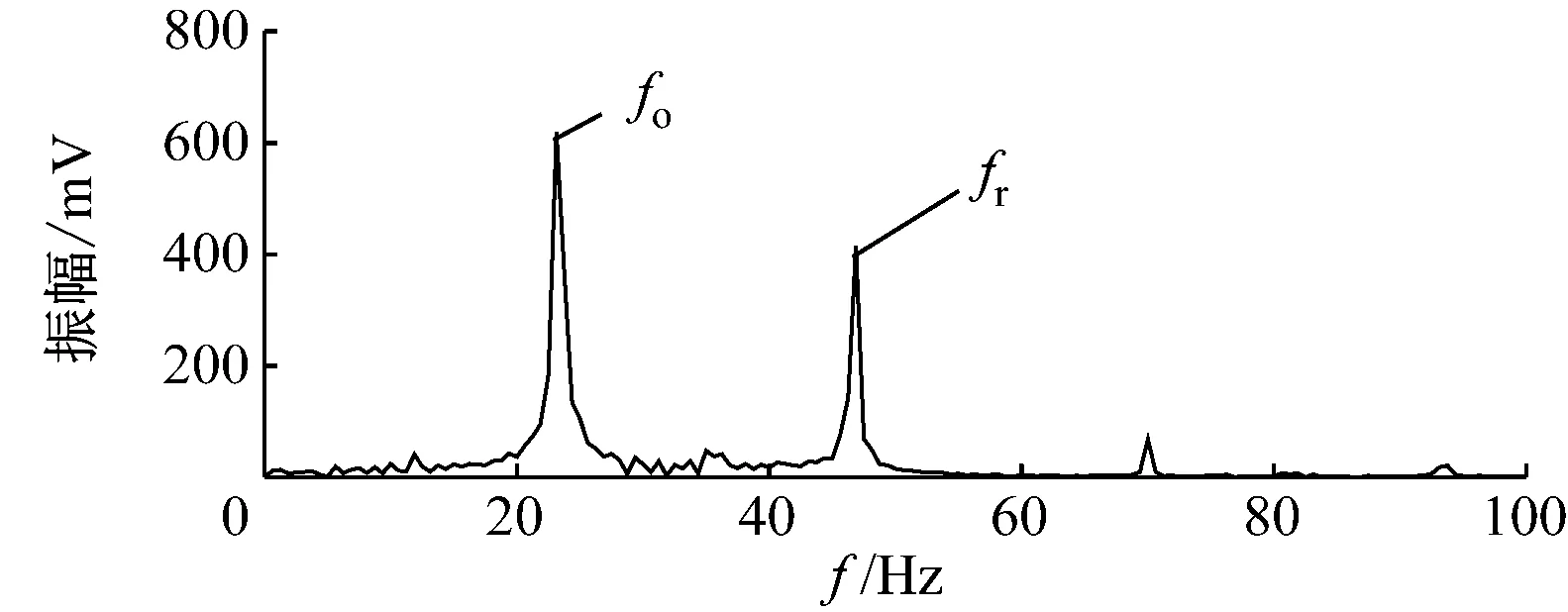
(b) 油膜涡动信号的频谱图

为准确提取转子故障特征，对振动信号进行SSWPT分析，结果见图7。由图7可知，SSWPT方法能够准确提取转子油膜涡动故障的特征频率，时频图中能量高度集中在油膜涡动频率附近，且基频存在明显的调频现象，而这些现象在频谱图中是观察不到的。

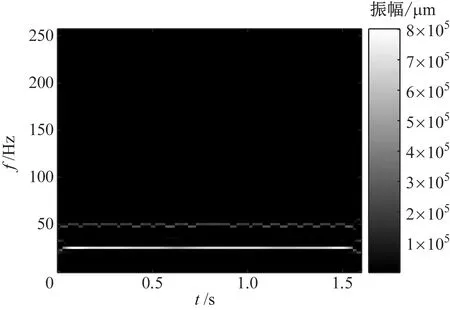
图7 油膜涡动信号的SSWPT时频图

为突出SSWPT方法的优越性，采用HHT方法对上述油膜涡动信号进行分析，结果如图8所示。

图8 油膜涡动信号的HHT时频图

由图8可知，通过HHT方法得到的时频图精度较低，能量扩散，且模态混叠现象严重，与SSWPT的时频图相比，HHT时频图不能充分体现油膜涡动故障的特征频率。

3.2 变转速工况下油膜涡动故障分析

通过控制转速调节装置，使转子转速均匀上升，模拟油膜涡动的演变过程。转子的转速由1 500 r/min上升至4 700 r/min，历时100 s，采样频率为1 280 Hz。由于故障数据点数较多，为提高计算效率，对故障数据进行降采样处理，设置降采样率为4，通过计算可以得到降采样频率为320 Hz。图9为转子升速过程中的振动信号时域波形及频谱图。由图9可知，转子发生油膜涡动时，其过程比较复杂，很难从时域图中发现油膜涡动的规律，且频谱图中存在频率模糊现象，不易识别油膜涡动故障的频率特征。

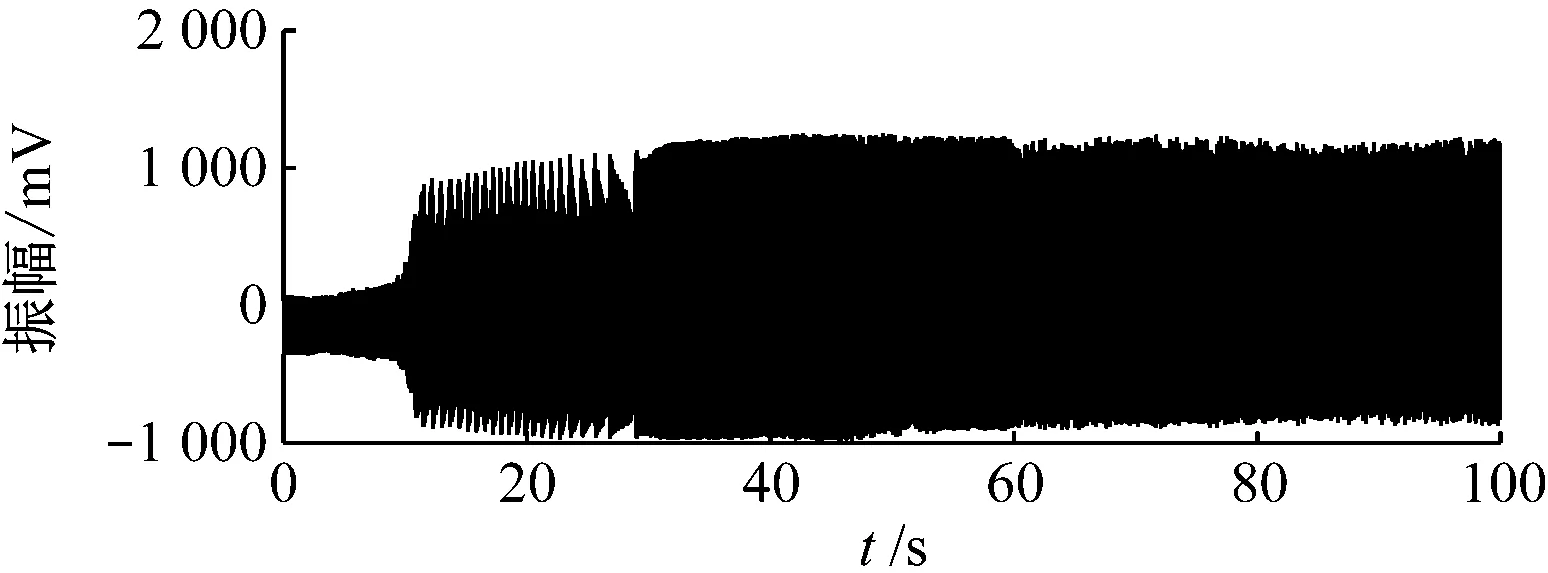
(a) 油膜涡动过程的时域波形图

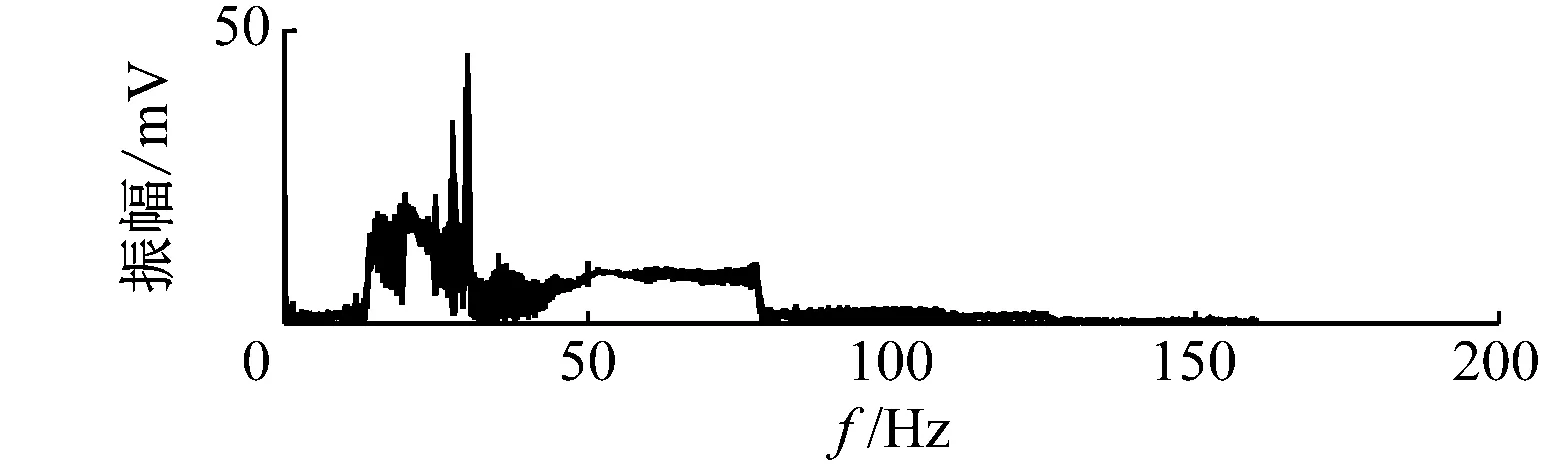
(b) 油膜涡动过程的频谱图

为准确分析转子升速过程中的振动信号，对该振动信号进行SSWPT分析，结果产生2个频率成分，分别为基频和涡动频率，如图10(a)所示。由图10(a)可知，当转速较低时，时频图的低频处只存在基频分量，说明转子系统没有发生涡动现象。10 s左右开始出现半频分量，油膜涡动从此刻开始；15 s左右油膜涡动频率出现振荡现象，且随着时间的变化基频出现调频现象；75 s后当转子转速接近2倍临界转速时，由于油膜涡动频率与转子1倍临界转速的基频重合，产生油膜振荡，此时随着转子转速的增加，油膜涡动频率不再增加，转子系统处于油膜振荡状态。图10(b)为HHT方法的分析结果，HHT时频图不易观察到油膜涡动频率随时间的变化规律。综上所述，SSWPT方法可以成功提取油膜失稳故障在变转速工况下的演化特征。

(a) 油膜涡动过程的SSWPT时频图

(b) 油膜涡动过程的HHT时频图

4 工程应用

采用某厂汽轮机转子油膜涡动故障数据进行分析验证。该汽轮机为超临界、一次中间再热、单轴、双缸双排汽、凝汽式汽轮机，型号C350/267-24.2/0.4/566/566。汽轮发电机组轴系共有7个支撑轴瓦，其中1号、2号轴瓦支撑高中压转子，3号、4号轴瓦支撑低压转子，5号、6号轴瓦支撑发电机转子，7号轴瓦为滑环轴转子外伸端的支撑轴瓦，滑环轴转子为发电机转子的外伸，各转子之间均采用刚性联轴器连接，轴系结构图见图11。

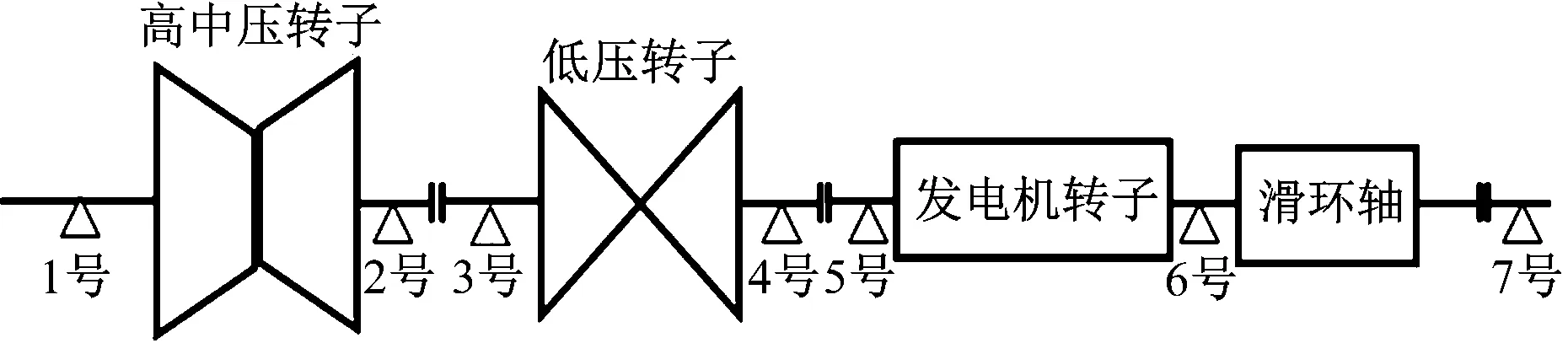
图11 机组轴系结构图

汽轮机的1号轴承在机组运行期间经常出现较大的不稳定振动。为分析机组故障，采用灵敏度为7.87 mV/μm的电涡流传感器测量1号轴承的径向振动，采集信号时机组处于额定工况附近。转子转速为3 000 r/min，采样频率为6 400 Hz，选取2 048个振动数据点进行分析，其波形及频谱如图12所示。从时域图可知，信号波形发生周期性变化，频谱图中存在转频及二分频，转频处幅值比较突出，但高次谐波幅值较低，仅根据频谱图诊断该机组转子故障类型的效果欠佳。

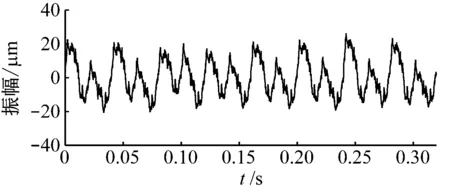
(a) 振动信号波形图

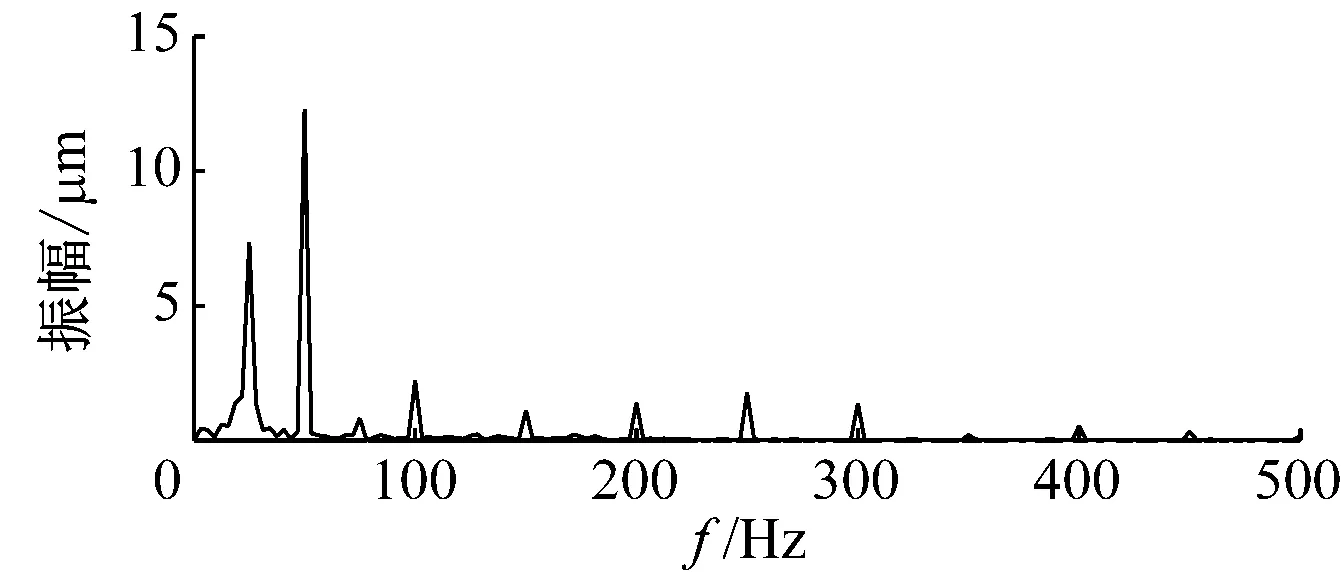
(b) 振动信号频谱图

为提取该机组转子的故障特征，并进行准确判断。采用SSWPT方法进行分析，结果如图13所示。图13能够清晰反映出机组振动信号的转频及二分频，且在转频、二分频及高频处存在调频现象。因此，可以判断出转子发生了油膜涡动故障。

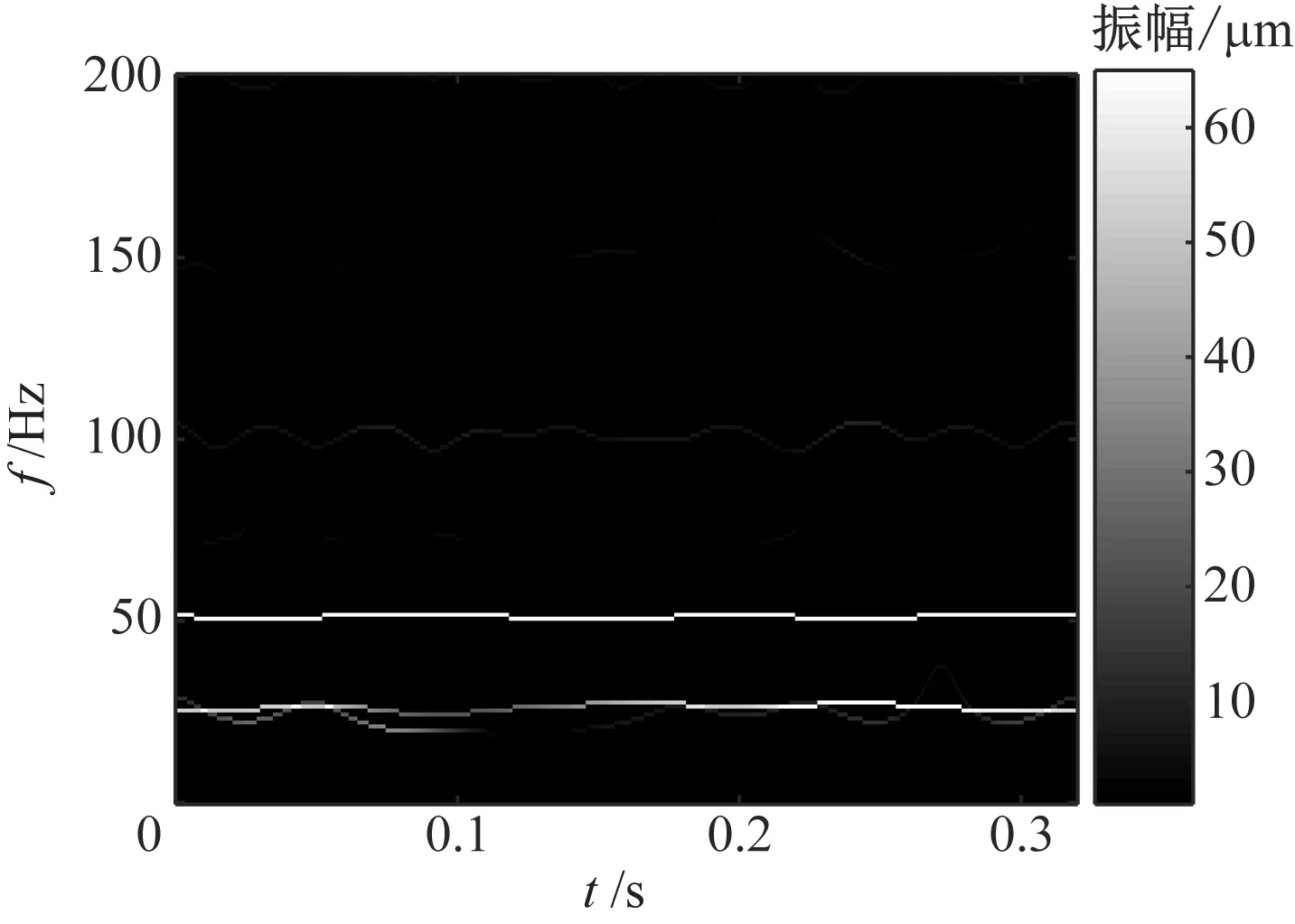
图13 振动信号的SSWPT时频图

对采集的振动信号进行HHT方法分析，结果如图14所示。图14中转子故障特征频率不明显，高频处存在大量的噪声干扰。因此，HHT方法不能有效提取转子故障特征频率，判别转子故障类型。

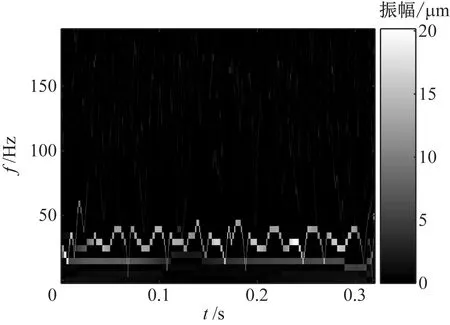
图14 振动信号的HHT时频图

5 结 论

(1) 模拟仿真及实验信号分析结果表明，与HHT方法相比，基于SSWPT的时频分析方法具有更高的时频精度，有效避免了模态混叠现象，能够准确提取油膜失稳故障在恒定转速工况下的故障特征频率及在变转速工况下的故障演化特征。

(2) 现场故障数据分析结果表明，SSWPT方法能够去除噪声干扰，可以精确地提取出转子的故障特征频率，更准确地诊断转子油膜失稳故障，为转子油膜失稳故障诊断提供了一种新的时频分析方法。