基于分子动力学模拟的近临界区CO2折射率异常波动分析

孙 辉，章立新，杨其国，刘婧楠，高 明

(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室，上海 200093)

超临界二氧化碳(S-CO2)动力循环系统因其优良特性在发电产业应用前景十分广阔[1]。超临界流体表现出介于气体与液体之间的中间特性，被广泛应用在工业技术领域中，成为重要的研究课题。对超临界流体的研究主要集中在宏观热力学性质上，也可以通过研究一些动态参数(如吸收系数αv)或静态参数(如折射率n和介电常数ε)来分析流体的微观特性[2]。折射率与密度、浓度间的关系是利用光学方法测量物性的重要基础。亚临界区气体介质的密度与折射率间的关系可直接由Gladstone and Dale经验公式表示，而对于超临界流体，因其物性的非线性变化，已有大量学者证明Lorentz-Lorenz公式在描述其折射率与密度间的关系时精度最高[3-4]。

由于CO2的临界状态(临界温度为304.13 K，临界压力为7.38 MPa)易于实现，很多学者对其折射率与物性间的关系进行了研究[2, 5-7]，其中光波长范围为447.1～667.8 nm，压力最高达240 MPa，温度最高达373.15 K。大部分实验是通过波长为632.8 nm的激光结合干涉法根据光斑条纹来获取CO2折射率。根据实验结果拟合出的洛伦兹常数，结合Lorenz-Lorentz公式可以计算出流体的密度；也可以通过折射率的变化间接反映超临界流体的相组成、溶质浓度和界面张力等性质。然而，上述实验中的工况都远远偏离临界状态。夏国正[8]和尹德益[9]采用光屏两点投射法对近临界区CO2折射率进行研究，发现当温度为304.25 K时，压力升至6.77 MPa后光斑飘忽不定，无法获得折射率的准确值，压力升至9 MPa后光斑恢复平稳；当温度为309.65 K时，压力升至7 MPa后因光线散射无法获得折射率，而压力升至10 MPa后光斑平稳。因此，CO2在近临界区的折射率数据仍存在较大空白。孙辉等[10]利用神经网络技术预测CO2的折射率，结果表明该方法在亚临界区和超临界区预测折射率的精度高，反演出的密度与美国国家标准与技术研究院(NIST)数据库计算值相比偏差小，但是在近临界区，由于训练集折射率的空白导致出现异常的非平滑曲线。从宏观来看，CO2在近临界区因压力的细微变化导致光斑舞动无法聚焦，这是因为在近临界区超临界流体的密度波动大，但此时并不能直观看到其微观结构究竟发生了怎样的异常现象。分子动力学模拟技术很早就被用来研究团簇体和大分子等微观结构，而目前使用最广泛的方法是分子动力(MD)模拟方法。在极端条件下，MD模拟中选择合适的力场模型可以避免复杂的实验，高精度地还原真实的分子微观状态，从而研究物质的输运特性和结构特征等。Bolmatov等[11]发现利用MD模拟方法结合液体声子理论可以解释超临界流体新的热力学边界线。Sohrevardi等[12]利用MD模拟方法分别研究了CO2、丙酮和水在一定工况下的输运特性，结果表明该方法能有效地揭示混合物的输运特性。

综上所述，虽然关于S-CO2光学性质的研究成果较多，但是其研究工况都远离临界区，对于近临界区折射率的异常波动未曾从微观层面给出直观的解释。因此，笔者利用MD模拟方法，通过径向分布函数(RDF)揭示近临界状态下CO2的微观结构特性，通过可视化软件展现近临界流体的聚类现象，并对密度时间序列曲线进行分析，可以直观地反映不同温度下近临界压力附近密度的剧烈波动。

1 MD模拟方法

CO2力场模型较多，已有学者对其模拟结果的绝对偏差和相对偏差进行了对比。结果表明，不同的力场模型对物理参数的预测精度不同。因此，在研究CO2物理参数时应选择合适的力场模型，以获得最佳预测效果[13]。比较各模型发现，EPM2、Zhang和SAFT-γ 3种模型使用最多且模拟表现优异。在本文研究中，密度对折射率发生异常现象的影响较大，考虑到不同模拟所参考的状态方程或实验参数不一，因此有必要对上述3种模型进行比较。

1.1 模型与势函数

本文模型使用的势函数有Lennard-Jones势和广义Mie势，后者的表达式为：

(1)

式中：E和rij分别为原子i与原子j之间的势能和距离；εij为势能阱深度，表明原子间相互作用的强弱；σij为原子间相互作用势为0的有限距离，与原子直径有关；m和b分别为斥力指数和吸引力指数；C为常数。

C是给定指数的函数，定义为：

(2)

当m=12，b=6时，C=4，式(1)表示标准的12-6 Lennard-Jones势，是描述双原子短程相互作用最常见的势之一。表1中给出了所需的CO2模型参数。异对原子的相互作用参数可根据洛伦兹-贝特洛组合规则(Lorentz-Berthelot combining rules)计算[14]。

(3)

式中：σii和σjj为相同原子间相互作用势为0的有限距离；εii和εjj为相同原子的势能阱深度。

对于库仑长程相互作用，采用基于原子的电荷模型，其表达式为：

(4)

式中：qi和qj分别为2个原子的电荷；ε为真空介电常数。

对于Zhang和EPM2模型，由于其属于刚体模型，因此只考虑原子间能量。

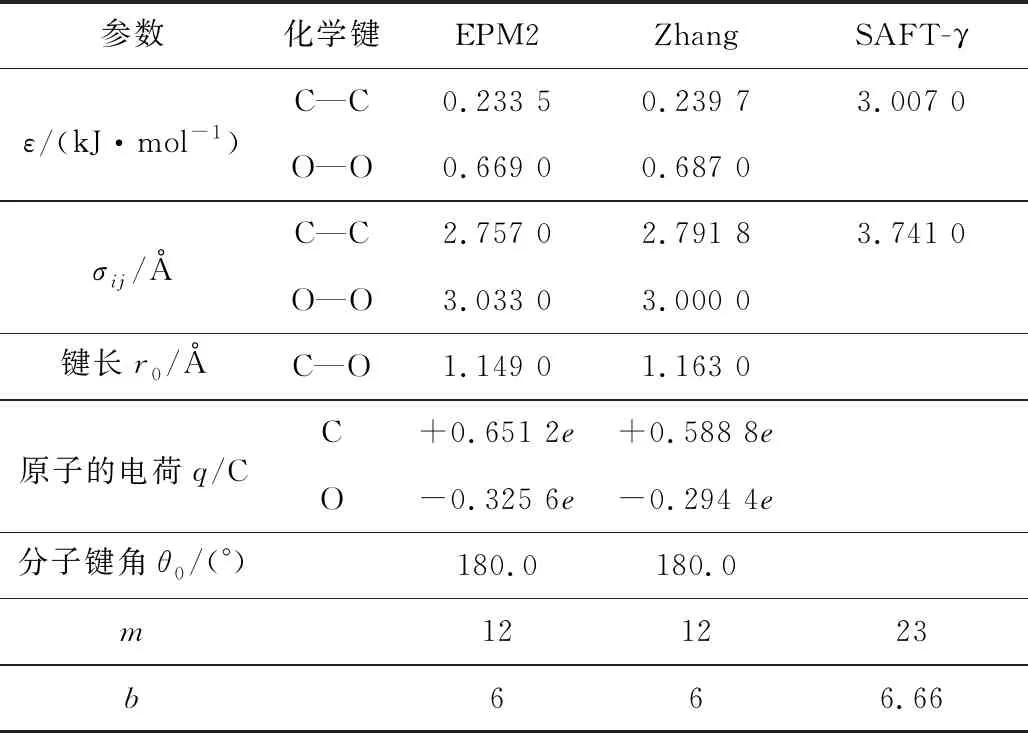
表1 力场模型参数

1.2 物理模型

通过自编程建立了包含1 000个CO2分子，边长为10 nm的立方体盒子(见图1)，并将系统设定为等温等压系综(NPT)，所有的模拟都是在LAMMPS开源软件中进行的。系统在x、y、z3个方向上均采用周期性边界条件。模拟过程中，对单位点模型采用 Nose-Hoover非哈密顿运动方程，而对刚体模型则采用Kamberaj描述的算法。设定时间步长为1 fs，将运动方程与Velocity-Verlet算法相结合，在各时间步长下更新原子的位置和速度。在每个温度和压力下，共运行500万次，前300万次使系统达到平衡状态，后200万次的结果每100 fs输出一次，作为最终各模型的比较数据。潜在的截断值设为4σ(σ为尺寸参数)。密度输出后取平均值，并与REFPROP软件给出的密度进行比较，从而对各模型进行评价分析。选取密度平均相对误差最小的模型进行后续分析。

图1 物理模型

由于笔者主要研究CO2在近临界区折射率异常现象的影响因素，于是在温度T为300 K、305 K和310 K，压力p为5.5～15.5 MPa状态下对3种物理模型进行了模拟，结果如图2所示。

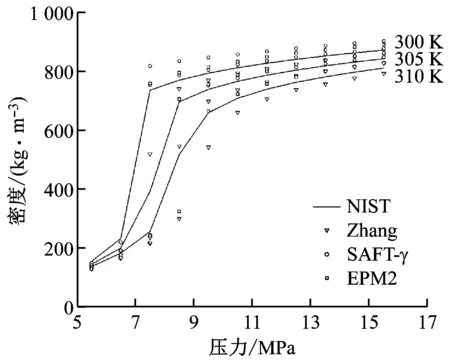
(a) 各模型预测密度与NIST预测密度的对比

(b) 不同温度下的平均相对误差

由图2可知，不同工况下3种模型预测所得的CO2密度的变化趋势与NIST预测值一致，总体偏差较小，但存在极个别偏差较大的数据点，恰在近临界区。从图2(a)可以看出，EPM2模型预测值与NIST预测值最接近。从图2(b)可以看出，EPM2模型在温度300～310 K、压力5.5～15.5 MPa内的平均相对误差最小。Zhang、SAFT-γ和EPM2模型的平均相对误差分别为8.87%、9.66%和6.34%。因此，选用EPM2模型进行分析。

2 结果及分析

2.1 径向分布函数分析

径向分布函数gm(r)为：

(5)

式中：N为系统的分子数目；dN为距参考分子中心距离r到r+dr间的分子数目；ρs为系统的密度。

径向分布函数表示系统区域密度与平均密度之比，可以描述系统的结构性质。径向分布函数通常会出现高低不同的峰谷，这是因为随着r的变化，区域密度与平均密度的比值随之改变，一般来说在距离参考分子较远处区域密度与平均密度相同，即径向分布函数值在1附近波动。通过计算得到不同压力下径向分布函数随温度的变化趋势，如图3所示。

(a) p=5.5 MPa

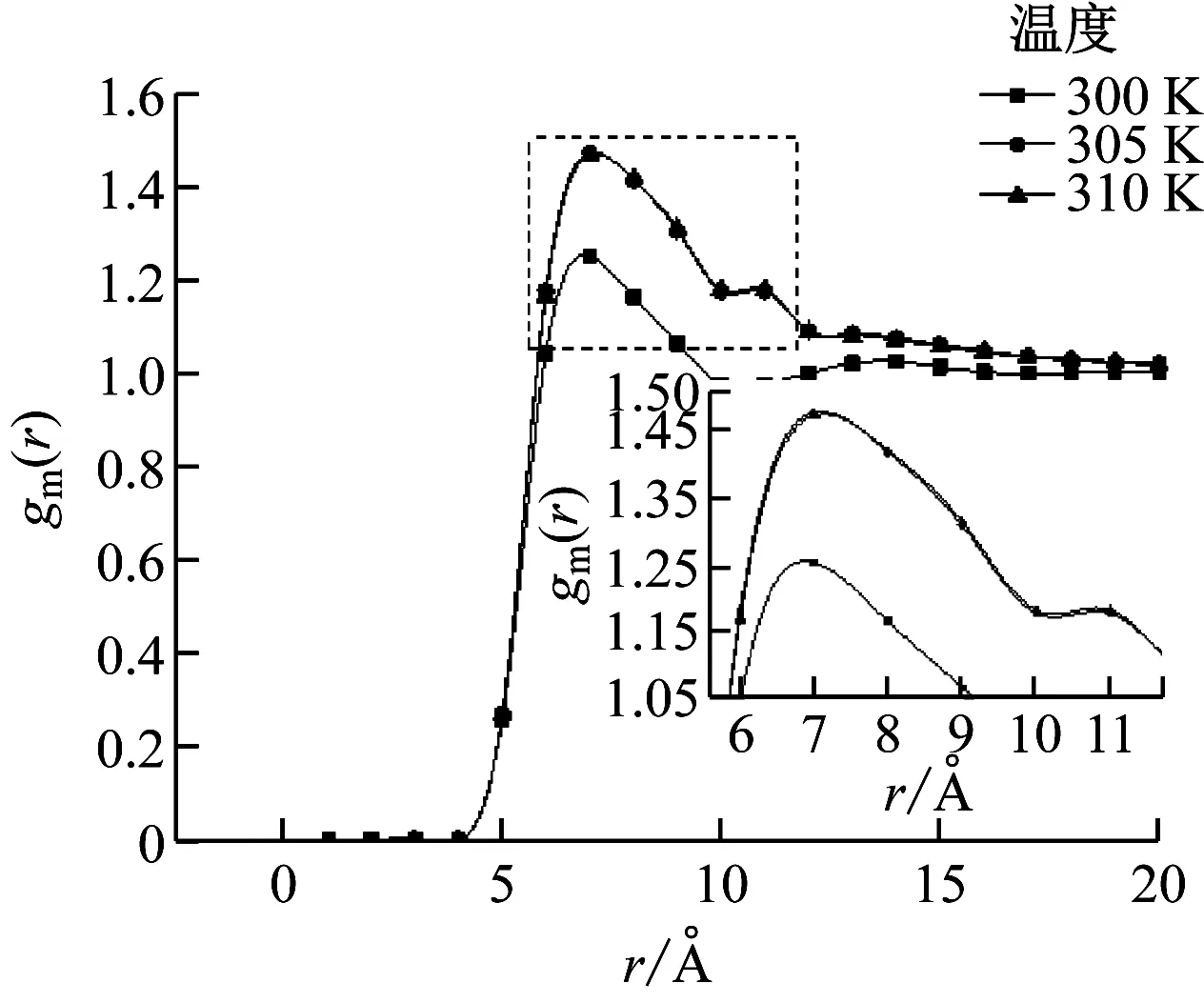
(b) p=7.5 MPa

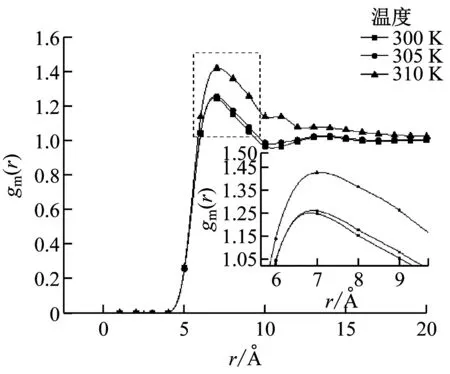
(c) p=8.5 MPa

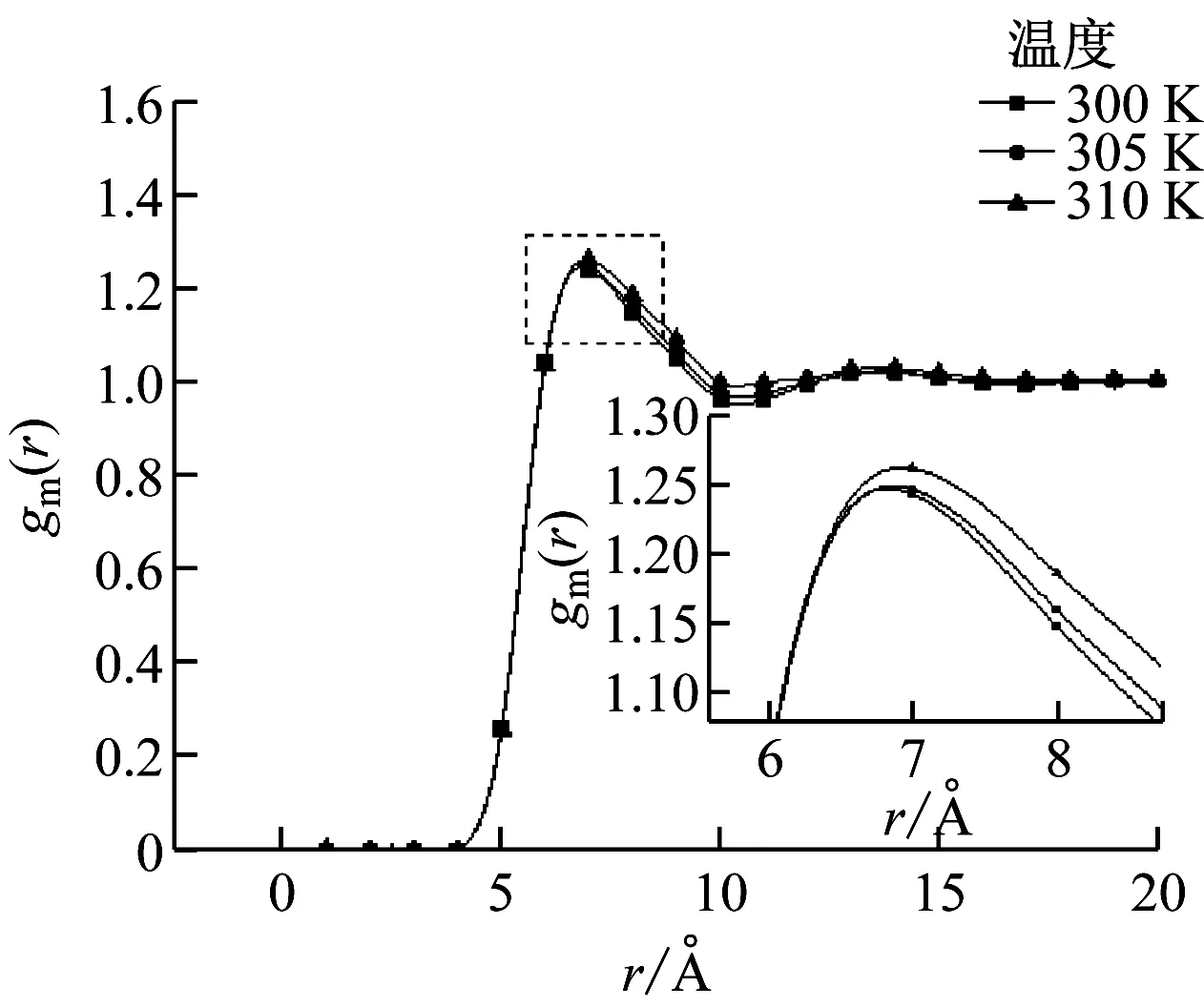
(d) p=9.5 MPa

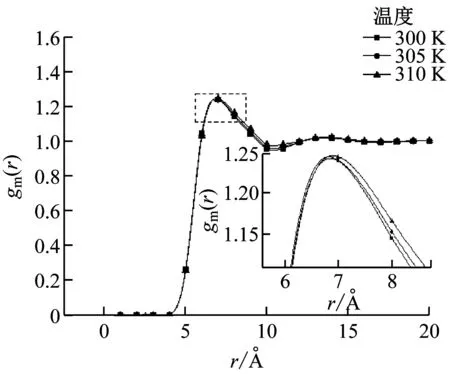
(e) p=10.5 MPa

(f) p=12.5 MPa

由图3(a)可知，当压力低于临界值时，随着温度的升高，径向分布函数的波峰逐渐减小，这是由于CO2逐渐由液态过渡到气态，系统的区域密度逐渐减小。由图3(b)可知，压力为7.5 MPa时，随着温度的升高，径向分布函数的峰值先升后降，差别很大。300 K时的峰值急剧下降，表现出类气体的异常行为，导致这一现象的实际原因是温度和压力均接近临界值，分子间形成部分团簇，而在聚类情况下，系统的区域密度与平均密度十分接近，因此其峰值只有1.25。而后随着温度的继续升高，系统逐渐过渡到超临界状态，展现出类液体现象。同理，由图3(c)可知，当压力为8.5 MPa，温度分别为300 K和305 K时，系统表现出聚类特征，直至温度升至310 K时才过渡到类液体的超临界区域。由图3(d)～图3(f)可知，当压力远离临界值时，温度的变化对结构特征的影响不大，超临界流体为高度的压缩性流体，密度逐渐增大，整个系统形成巨大团簇。

聚类分析可以通过OVITO软件直观地展现出来，以温度为305 K，压力分别为7.5 MPa、10.5 MPa为例，画出系统平衡后某一时刻的粒子位置图(见图4)，设定分子间截断距离为3.5 Å(1个CO2分子的大小约为2.5 Å)，在此范围内的分子称为1个簇。

图4(a)给出了压力为7.5 MPa时的分子聚集状态，其最大团簇含有80个分子，最小团簇含有1个分子，共形成446种团簇。图4(b)中压力为10.5 MPa时只含有24种团簇。实际上，这些聚集体、团簇的形成会改变CO2的光学性质(如线性和非线性折射率)[15]。在聚类出现的情况下，超临界流体的Lorentz-Lorenz公式[16]为：

(6)

实际上，在强光场中，折射率n还与光强有关，式(6)中n=n0+n2E2,n0为线性折射率,当非线性折射率n2=0时，n=n0。若存在单个分子和团簇共同存在的二元混合物，其非线性折射率n2可表示为：

(7)

式中：RLL为洛伦兹常数；β为单个分子的极化率；β2为包含多个分子团簇的极化率；mmol为分子的质量；s为团簇中的分子数；N、N1和N2分别为分子总聚集度、单个分子聚集度和团簇聚集度，N=N1+N2s；γ为形状因子，对于任意的簇，0.5<γ<1。

(a) p=7.5 MPa

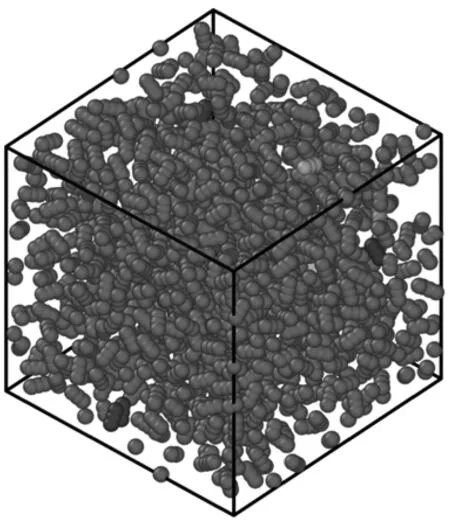
(b) p=10.5 MPa

图5给出了不同温度下的团簇种类个数与压力的关系。在不同温度下，随着压力的变化，团簇种类个数差异很大。当压力处于亚临界状态时，团簇种类少，几乎是单个分子成为1个个体，非线性折射率几乎为0，但是随着压力的升高，尤其在临界值附近，聚簇和解聚同时发生，团簇种类和数量波动剧烈，单个分子和疏密不同的团簇多元共存，团簇密度和系统整体密度剧烈变化，折射率也呈现出强烈的非线性变化。从OVITO软件分析来看，团簇种类个数在不同瞬态波动较大，随着压力继续升高，聚簇动力增加，团簇种类个数明显减少，系统形成1个巨型团簇(图4(b)中分子聚集程度较图4(a)密，说明在10.5 MPa压力下，团簇种类个数减少)。此时团簇内的总分子数目几乎不变，在Widom线(即超临界区类液体与类气体的分界线)[17-18]附近达到极大值。当压力高于Widom线时，随着压力的升高，形成巨晶层，折射率的非线性也不明显了。

图5 不同温度下的团簇种类个数

根据费马最小时间原理，在两点之间所有的可能路径中，光会选择耗时最少的路径[19]。射线在介质中每点的速度是c0/n(c0为真空中的光速)，因此射线需要寻找一条优先通过折射率小的路径。从结构特性来看，近临界区团簇种类繁杂，变化剧烈，射线每次通过路径所需的时间不同，所以从光屏来看，会产生无规则的长条状。

2.2 密度时间序列曲线分析

密度时间序列曲线可由Lammps直接输出，通过其波动规律来描述混沌和类随机特性[20]。笔者主要通过时序时间来直观展现近临界区CO2密度的剧烈波动，从而解释近临界区CO2异常的光学现象。图6为不同压力下的密度时间序列曲线图。从图6可以看出，随着温度变化，不同压力下的密度波动程度也随之变化。

(a) 300 K

(b) 305 K

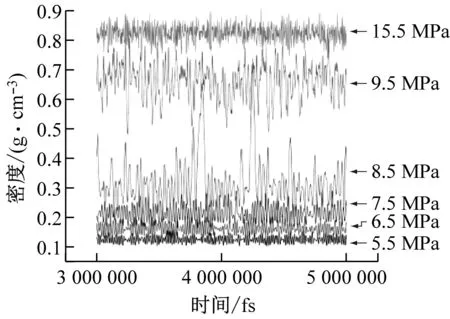
(c) 310 K

当温度低于临界值时，密度会在临界压力处剧烈波动；当温度超过临界值时，密度会在近临界压力处剧烈波动，这与上述对径向分布函数的分析结论一致。从密度时间序列曲线来看，在远高于临界压力和低于临界压力处，密度的波动逐渐呈现出规则化。这是由于前者生成了稳定的团簇体，而后者是稳定的单分子，而在近临界区，分子聚簇和解聚变化剧烈，团簇种类繁多，所以密度波动很大。

3 结 论

(1) 通过径向分布函数的分析和聚类现象的可视化，从微观层面揭示了CO2折射率在近临界区出现异常的原因，即由于近临界区CO2的单分子和团簇体多元混合，团簇密度波动，进而影响光对最短路径的找寻，从而产生非线性折射率。这种情况将随着压力的升高而消失，因为在远离临界压力后，系统内形成稳定的巨型团簇，不会出现明显的非线性折射。

(2) 在近临界区CO2密度时间序列曲线出现混沌，系统密度发生剧烈波动，根据Lorentz-Lorenz公式，密度的波动会直接引起折射率的剧烈波动。

(3) 综合结构特征和密度时间序列曲线来看，在测量近临界区CO2折射率时，可以对瞬态的折射率进行抓拍。类比密度时间序列曲线，只要瞬态图形足够多，就可进一步分析求解出平均折射率，亦可以根据Lorentz-Lorenz公式对近临界区的折射率进行预测。