复数滤波器型锁相环的改进控制策略*

何 宇周道龙邓小龙罗 琦

(1.江苏信息职业技术学院智能工程学院，江苏无锡 214153；2.南京信息工程大学自动化学院，江苏南京 210044)

并网逆变器是分布式发电系统的重要组成部分，作为功率接口单元，承担着把可再生能源发出的电能输送到公共电网的使命[1-2]。在并网逆变器的控制中，锁相环(Phase-Locked Loop，PLL)起着至关重要的作用:对逆变器的输出电流进行控制时，PLL的作用是提供电网电压的相位，通过相应控制，使输出电流与电网电压同相或呈一定的相位差，以确保逆变器的可靠运行[3]；在孤岛检测中，PLL 的作用是提供电网的频率或幅值，当电网发生停电故障时，防孤岛控制可根据这些信号的变化判断出孤岛是否存在[4]；在低电压穿越中，PLL 的作用是提供电网的基波正负序分量(Fundamental Positive-and Negative-Sequence Components，FPSC/FNSC)，当电网发生幅值跌落时，低电压穿越控制可进行相应的无功补偿[5]。因此，PLL 技术在逆变器并网系统中扮演着一个不可或缺的角色，值得深入研究。

在三相电力系统中，对PLL 的研究主要有同步坐标系PLL(Synchronous Reference Frame PLL，SRFPLL)[6]、二阶广义积分器PLL(Second-Order Generalized Integrator PLL，SOGI-PLL)[7]、自适应陷波器PLL(Adaptive Notch Filter PLL，ANF-PLL)[8]、滑动平均滤波器PLL(Moving Average Filter PLL，MAFPLL)[9]和复数滤波器PLL(Complex Coefficient Filter PLL，CCF-PLL)[10-15]等。其中，由Guo Xiaoqiang等[10]提出的CCF-PLL 由于控制结构简单、算法易于实现和系统响应速度快等优点成为近年来备受关注的一种新型电网同步方法。该PLL 的前置滤波器——CCF 在电网基波的正负频率处都能产生谐振尖峰，具有正负频率的选择性，无需对称分量法即可精确分离出FPSC 和FNSC。Li Weiwei 等[11]运用复数系统理论更全面、更深刻地阐述了CCF 技术，并提出了可使高次谐波衰减更快的三阶CCF 方案。Golestan 等[12]指出，以往对此类前置滤波器型PLL分析时，通常将前级滤波器和后级PLL 作为分立系统处理，而不考虑两者间的相互影响，因而无法准确描述整个系统的动态性能。Golestan S，Monfared M等[12-14]将CCF-PLL 的前后两级结合起来分析，对整个系统作了数学建模和参数设计，通过对比实验发现:相比其他先进PLL，CCF-PLL 在动态性能上并无突出优势[12-14]。Quan Xiangjun 等[15]通过理论论证表明:CCF 虽然结构简单，但本质上其系统传递函数与实数滤波器(如SOGI)是一致的，因此CCFPLL 的控制性能同实数滤波器PLL 相比并无多大差别，其动态品质有待提高。

为改善CCF-PLL 的动态性能，提出了一种提升系统相角裕度的改进复数滤波器PLL。该PLL 将输出角频率对CCF 结构的单位反馈改成了角频率的比例项和积分项分别进行线性反馈。通过建立所提PLL 的状态空间表达式，求得了其系统传递函数。分析后发现，要保证系统的准确性，只要使角频率的积分项呈单位反馈，而调整比例项的反馈系数可使系统中频区宽度和相角裕度得以改变，从而达到改善动态品质的目的。理论分析、仿真验证和对比实验表明，所提PLL 在保持CCF-PLL 原有优势的同时显著提高了系统的动态性能。

1 CCF-PLL 性能分析

采用的CCF-PLL 如图1[10-15]所示。

图1 中:Uabc为三相电网电压；Uαβ为Uabc的αβ轴分量；ωp、ω0分别为CCF 结构的截止角频率和反馈角频率；为理想电网的角频率(100π rad/s)；分别为CCF-PLL 提取的FPSC、FNSC、角频率和相位；的dq轴分量。

由图1 可知，CCF-PLL 由前级CCF 结构和后级SRF-PLL 组成。前级负责将Uabc的FPSC 和FNSC分离出来；后级负责将FPSC 中的幅值、相位和频率等信息精确提取出来。

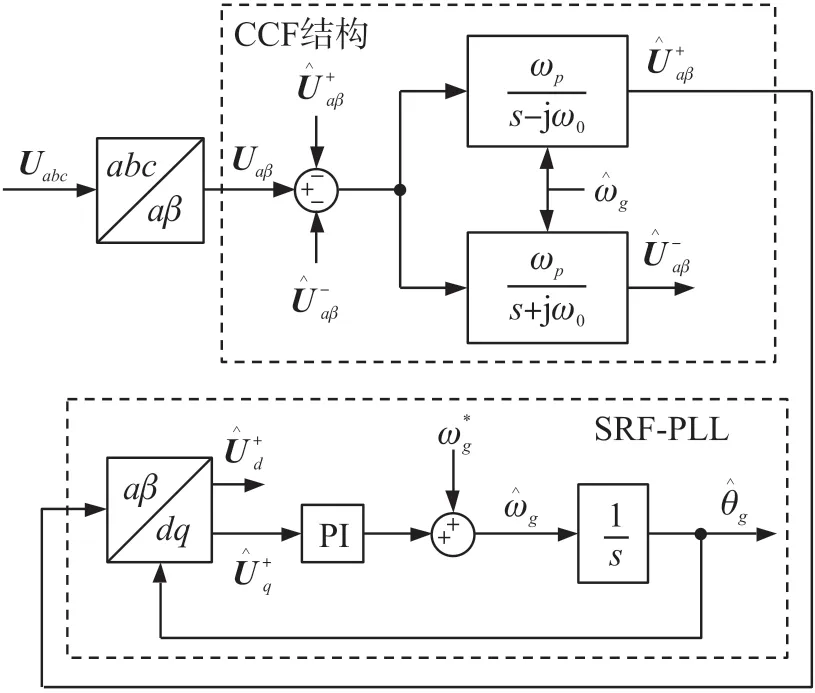
图1 基于CCF 结构的三相PLL

分析该PLL 时，将前后2 级作为独立系统看待，分开处理[10-11]。后级提取出的反馈至前级供复数系统使用(如此反馈可使CCF 结构在电网频率变化时能自适应地对频率作出调节)，两者之间必然存在一定联系，不能看成是分立系统，必须结合起来研究[12]。通过数学建模得到CCF-PLL 的数学模型如图2 所示[12-14]。

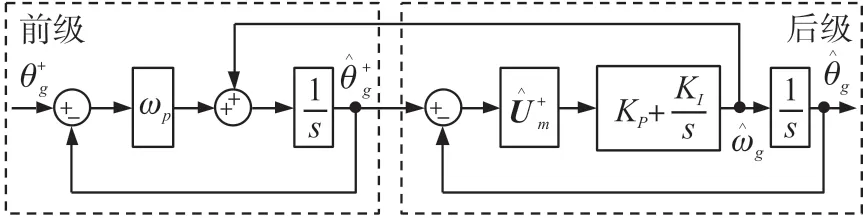
图2 CCF-PLL 的数学模型

根据系统结构图的等效变换法则，可将图2 所示框图可进一步等效为图3。

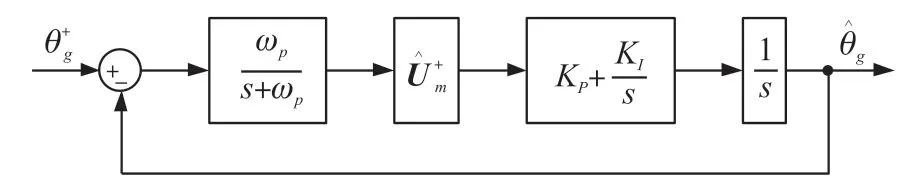
图3 CCF-PLL 的等效数学模型

Golestan 等[12-13]指出，CCF-PLL 与SOGI-PLL、ANF-PLL 等前置滤波器型PLL 的数学模型是一致的；Quan Xiangjun 等[15]运用状态空间分析法也得出了相似结论。因此，CCF-PLL 虽然控制结构简单，但其动、静态特性同上述实数滤波器型PLL 在本质上是相同的。

为改进CCF-PLL，先分析其控制性能。

由图1 容易求得Uαβ到的传递函数F(s)为:

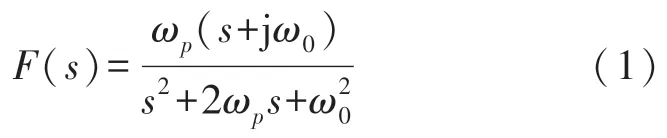
对照二阶线性系统的标准形式，可得:

式中:ζ、ωn分别为二阶系统的阻尼比和自然频率。

消去式(2)中的ωn，解得:

取ζ为最佳阻尼比0.707、取ω0为理想电网角频率100π rad/s，则ωp的取值为:

由图3 可得该系统的开环传递函数G1(s)为:

根据式(5)，可绘出该系统的频率特性曲线如图4 所示(这里以相角裕度取最大值示例)。

图4 G1(s)的频率特性曲线

图4 中，ωc、γ分别为开环系统的截止频率和相角裕度；ω1、ω2为频区交接频率。

由式(5)可得:

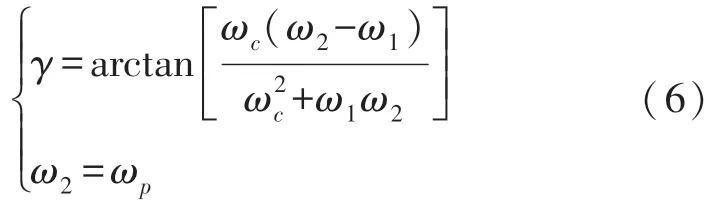
这里需说明的是，由式(5)得到图4 和式(6)应满足KI/KP＜ωp，否则系统幅频特性曲线的斜率为-40 dB/dec～-60 dB/dec～-40 dB/dec，导致系统不稳定[16]。

经过研究得出:ωc的取值在1/5～1/4 的2 倍电网角频率时可兼顾系统的快速性和抗干扰性。这里对ωc的取值同文献[13]，为:

由控制理论的三阶最佳设计法[13，16]可知，当ωc为中频区的几何中心时，系统的相角裕度最大，即:

由式(8)可得:

将各已知数据代入式(6)的γ，可得:

此时系统的中频区宽度H为:

经典控制理论[16]指出，设计一个良好的控制系统，要将其相角裕度设定在45°左右(对应的中频区宽度为5.83)。过低于此值，系统的动态性能较差，对参数变化较敏感；过高于此值，系统的稳定程度过好，动态过程会变得很缓慢。因此，CCF-PLL 的中频区宽度和相角裕度过低，有必要进行改进。

2 改进型CCF-PLL 性能分析

2.1 系统结构

改进型CCF-PLL(Improved Complex Coefficient Filter PLL，ICCF-PLL)的整体结构图如图5 所示。

图5 ICCF-PLL 的系统框图

对比图1 和图5 可知，ICCF-PLL 的改进之处在于将的比例项和积分项分别进行线性反馈，而不是简单的单位反馈；如此反馈引入的两个参数k1和k2(0≤k1，k2≤1)扩展了系统控制的自由度(CCFPLL 可看成是ICCF-PLL 在k1＝k2＝1 时的特例)，更有利于校正系统，从而改善系统的动态品质。

2.2 系统分析和设计

仿照CCF-PLL 的建模方法，可得ICCF-PLL 的数学模型如图6 所示。设u、y、x分别为系统的输入变量、输出变量和状态矢量，即:

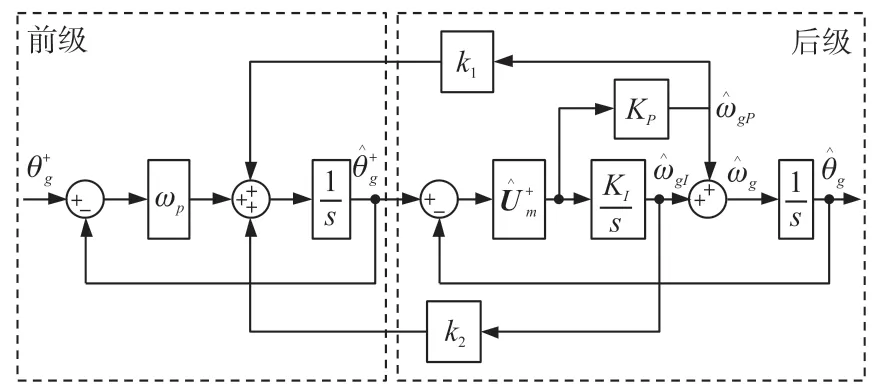
图6 ICCF-PLL 的数学模型

根据状态空间分析法，可得图6 所示系统的状态空间表达式为:

式中:A、b、c的具体表达式如式(14)所示。

根据传递函数公式Φ＝c(sI-A)-1b，可得该系统的传递函数Φ(s)为:

其等效开环传递函数G2(s)为:

由于u＝为一斜坡输入，要使捕获的相位能稳定地、无静差地跟踪实际相位，式(16)所示的开环系统必须为Ⅱ型系统，故:

此时的G2(s)为:

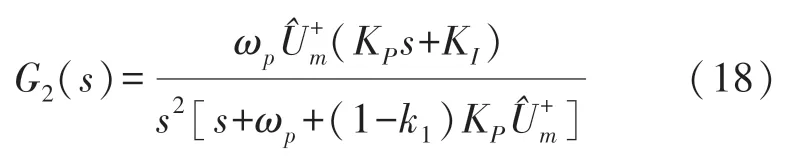
对比式(5)的G1(s)和式(18)的G2(s)可知，改进后系统的低频区-中频区交接频率ω1未发生改变，而中频区-高频区交接频率ω2增大了、并随系数k1的变化而变化，因此合理调节k1即可适当加宽中频区宽度，使系统相角裕度提高至一个合适值。

由式(18)可得ω1、ω2和ωc如式(19)所示。

这里仍采用三阶最佳设计法校正系统，即ω1、ω2和ωc的关系仍满足式(8)。由式(8)和式(19)可得G2(s)的相角裕度如式(20)所示。

由于前级结构中Uαβ到的传递函数未发生变化，因此ωp仍取为222.11 rad/s；为具有可比性，ωc的取值与CCF-PLL 相同，即ωc为138.23 rad/s。根据式(20)，绘出k1变化时γ的曲线如图7 所示。

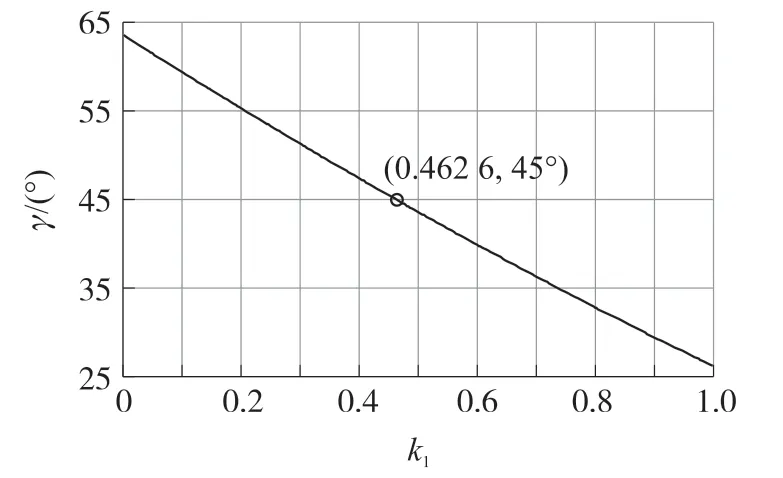
图7 k1变化时G2(s)的相角裕度曲线

由图7 可以看到，G2(s)的相角裕度γ随着k1的减小而增大，要使γ设定在45°，k1的取值为:

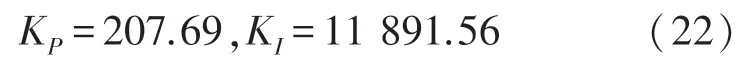
对应的中频区宽度为:

此时G2(s)的Bode 图如图8 所示。

图8 G2(s)的Bode 图

由式(23)和图8 可知，改进后系统的中频区宽度由原来的2.58 提高至5.83、系统的相角裕度由原来的26.21°提高至45°。动态指标的合理提升势必会使所设计系统具有一个良好的过渡过程，从而改善系统的动态性能。

3 仿真验证

为测试所提ICCF-PLL 算法的正确性，利用MATLAB/Simulink 对此算法进行了仿真验证。仿真中设置电网在0～0.25 s 内处于理想状态:相电压幅值为311 V(1 pu)、频率为50 Hz，无负序、无谐波；0.25 s 后，频率突变至55 Hz，相位跳变+25°，并注入25%的负序。仿真结果如图9 所示。

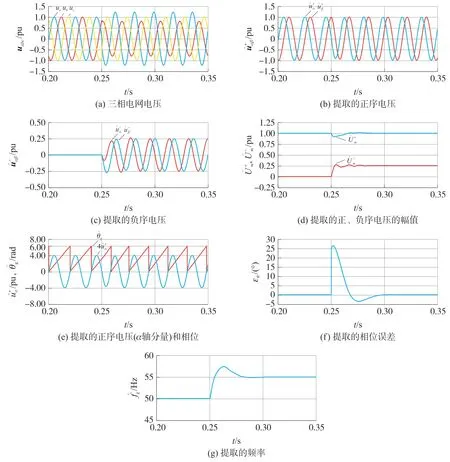
图9 仿真结果

图9(a)～图9(c)表明，ICCF-PLL 在电网变化前后均能顺利分离出正负序分量；图9(d)显示，正负序电压的幅值能快速、无偏差地稳定在预设值(1 pu 和0.25 pu)。因此，该PLL 具备快而准的正负序分离能力。

4 实验验证

为进一步验证ICCF-PLL 的动态性能，将其与CCF-PLL 进行了对比实验，选用TMS320F28335 DSP 作为控制芯片，内部变量(如电压、幅值、频率和相位等信息)由DAC7725 数模转换芯片输出，设置DSP 的采样频率为20 kHz，实验中对“频率突变+5 Hz”、“相角跳变+25°”、“注入25%的负序”及“加入20%、15%的-5 次和+7 次谐波”这4 种电网变化情况进行验证，实验结果如图10～图13所示。

图10 频率突变下的实验结果

图11 相位跳变下的实验结果

图12 注入负序下的实验结果

图13 加入谐波下的实验结果

在稳定性和准确性方面:由图10～图12 可知，ICCF-PLL 在电网频率突变、相位跳变和存在负序的情形下都能成功提取出电网的正负序分量、频率和相位。由正负序的幅值曲线、频率响应曲线和相位误差曲线可以看出，其稳态值都能在较短时间内无静差地跟踪预设值或0，说明所设计的PLL 是一个稳定的无差控制系统，能够精确地进行正负序分离、锁频和锁相。

在动态性能方面:图10(c)、图11(c)和图12(d)给出了CCF-PLL 及ICCF-PLL 在提取电网频率和相位误差上的对比结果。为能更具体对比两者在动态性能上的表现，表1 列出了它们的动态指标值。可见，在不同电网情况下，ICCF-PLL 的频率超调量和相位误差超调量都要比CCF-PLL 小；尤其是第2 次偏离稳态值的超调要比CCF-PLL 小得多，均小于CCFPLL 的1/2，有的甚至达到了1/10、1/15。结合表1 的调节时间可以看到，ICCF-PLL 在收敛于稳态值的动态调节过程中展现出的衰减程度要比CCF-PLL 大得多，并且衰减速度更快。因此，相比CCF-PLL，ICCFPLL 拥有一个更好的动态行为。

在谐波抑制方面:由图13 可知，在如此恶劣的电网环境下，ICCF-PLL 依然能较为准确地提取出电网各信息。分离出的正序电压的THD 为3.32%，其中-5 次、+7 次谐波的百分比分别为2.21%和1.77%(如图13(d)所示)，谐波含量大大降低；正序幅值的最大波动值为0.05 pu；频率的最大波动值为0.7 Hz，而其在CCF-PLL 下为1 Hz；相位误差的最大波动值为0.2°，而其在CCF-PLL 下为0.3°。因此，较之CCFPLL，所提PLL 对电网谐波的抑制能力更强。

表1 CCF-PLL 与ICCF-PLL 的动态指标值

5 结论

在CCF-PLL 的基础上，提出了一种可提高系统动态性能的新型PLL 技术，即ICCF-PLL。通过理论分析、仿真验证和对比实验，可得出如下结论:

(1)在三阶最佳设计法下，CCF-PLL 的相角裕度仅为26.21°，动态性能较差；

(2)ICCF-PLL 在CCF-PLL 的基础上引入了反馈系数，合理调节相关系数，即可保证系统准确性，又可加大中频区宽度，从而提升相角裕度；

(3)采用相同的开环截止频率，ICCF-PLL 在三阶最佳设计法下的相角裕度可调整至45°；

(4)在电网频率、相角和负序突变时，ICCF-PLL都能准确进行正负分离、锁频和锁相，提取的频率和相位误差的超调量比CCF-PLL 更小，系统的调节时间更短，表现出的动态性能更优异；

(5)在畸变电网环境下，相比CCF-PLL，ICCFPLL 更能抑制电网谐波对系统输出的影响。