燃煤电厂节能改造机组节能计算方法研究

韩建春，荀 华

（内蒙古电力科学研究院，内蒙古呼和浩特 010020）

0 引言

当前，燃煤电厂为了最大限度地提高机组热经济性开展了多种形式的节能改造，其中包括锅炉烟气余热利用改造、给水泵改造、供热改造等。在这众多改造形式中，有些改造后的节能量是随机组负荷变化而变化的，也就是说改造节能量与机组负荷有相对稳定的对应关系，如锅炉烟气余热利用改造。近年来，为了能够准确获得此类改造后的节能量，产生了不少节能量的计算方法。本文通过对发电厂热力系统参数分析，结合数值拟合及积分平均算法，得出一种较为简单准确的节能量计算方法。

1 当前节能量计算方法及缺陷

1.1 当前节能量计算方法

对于节能量随机组负荷有明显变化的节能技术措施，采用计算额定负荷100%、75%、50%等3 个工况下的节能量，根据机组运行小时数中3 个负荷系数所占比例计算加权平均节能量。在计算过程中，85%额定负荷及以上的划归100%负荷，60%～85%额定负荷划归75%负荷，小于60%额定负荷的划归50%负荷。机组年节能量按式（1）计算[1]。

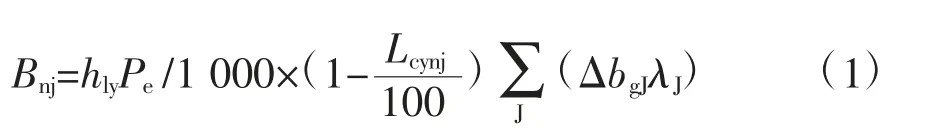
其中，Bnj为年节煤量，t；hly为年利用小时数，h；Pe为机组额定功率，MW；Lcynj为年发电厂用电率，%；ΔbgJ为负荷系数J 工况下供电煤耗下降，g/(kW·h)；λJ为机组统计期内负荷系数J 工况下累计发电量与总发电量之比；负荷系数J 工况分别指85%及以上、60%～85%额定负荷、小于60%额定负荷。

对于负荷系数J 工况下供电煤耗下降则采用2种方法测试。

方法一：在100%、75%和50%额定负荷工况下，利用热平衡法、等效热降法等节能分析计算方法计算节能设备的节能量。

方法二：在100%、75%和50%额定负荷工况下，按节能设备投入与退出情况进行针对性试验对比计算节能量。

1.2 当前算法存在的缺陷

当前的节能算法无疑可以获得节能量随机组负荷变化的节能措施的节能量，但却存在一定困难并存在较大的偏差。究其原因主要有两方面：一是随着电网容量的不断增大，电网峰谷差也不断增大，入网发电机组每日的负荷波动比较大，使得负荷统计按≥85%、60%～85%、≤60%负荷段进行精确统计变得及其繁琐，虽说现代计算机技术在生产中得到广泛应用，但依然有较大的运算量。另外，负荷的区段划分方法也缺乏相应的科学依据。二是节能措施的节能量与机组负荷存在相应的依变关系，仅采用某一负荷点节能量通过加权系数计算总体节能量的方法存在一定的计算偏差，而且采用机组统计期内负荷系数J 工况下累计发电量与总发电量之比作为权重的加权平均是否合理还有待验证。

为了有效解决以上问题，本文尝试将积分运算、数值拟合等数学方法应用到节能量计算过程中，实现较为简单的方法获得更为准确的节能量。

2 节能量的积分平均算法

2.1 节能量测试中排汽焓的确定

在节能量的测试中，采用方法二需要对每一个负荷工况进行投、切2 次测试，测试期间如果出现参数波动较大往往会造成试验失败。因此方法一常作为测试的首选方法。

方法一推荐的利用热平衡法、等效热降法等计算方法中涉及机组的变工况计算，计算中需限定机组变工况后的边界条件，由于汽轮机通流面积固定，相同排汽压力下不同排汽流量下的排汽比容有所不同，由此将造成排汽干度及排汽焓的不同[2]。

为了能够准确推算出变工况后的机组排汽焓，采取对不同排汽流量下的排汽比容进行拟和计算获得排汽比容与排汽流量的关系[3]。

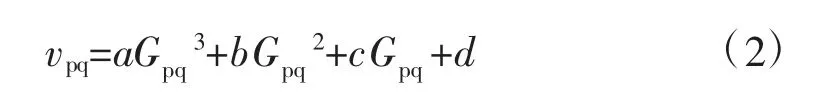
其中，vpq为排汽压力Ppq对应的排汽比容，m3/kg；Gpq为低压缸排汽流量，kg/h；a、b、c、d 为多项式系数。

其中，Xpq为低压缸排汽干度；v为排汽压力Ppq对应的饱和蒸汽比容，m3/kg。

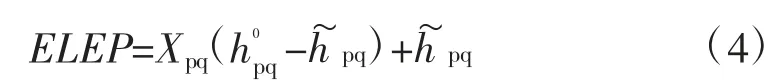
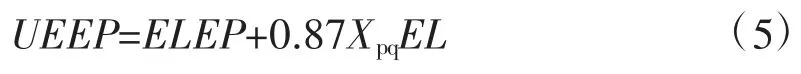
其中，UEEP 为低压缸有用能终点焓，kJ/kg；EL为排汽损失，kJ/kg。

由此便可准确推算出变工况后机组的排汽焓，利用此排汽焓通过能量平衡便可以得到更加准确的机组节能量[4-7]。

2.2 不同负荷下节能量的推导

汽轮发电机组在日常运行期间负荷是一个连续变化的过程，如果能够通过分析计算获得节能量随机组负荷变化的关联关系，不仅有助于获得机组各负荷下的节能量，而且可以避免繁琐的负荷段统计和加权运算。图1、图2 为某超临界350 MW 机组锅炉烟气余热利用改造后采用前述方法计算所得机组不同条件下的发电热耗率曲线及发电热耗率随负荷的减少量曲线。

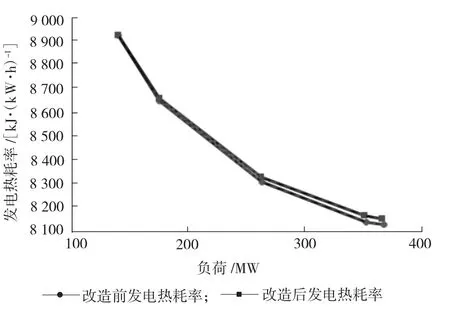
图1 发电热耗率曲线

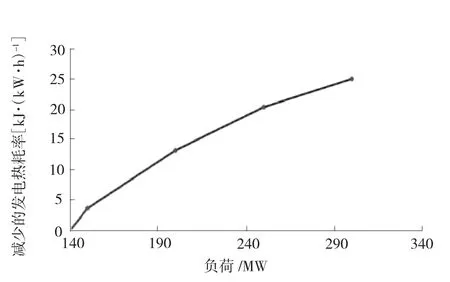
图2 发电热耗率随负荷的减少量曲线

由图1 及图2 可以看出，此机组的改造节能量与负荷有一种相互对应关系。因此，仍然可以尝试采用前述的数值拟合方式来获得一负荷与发电热耗率降低的关系曲线，即

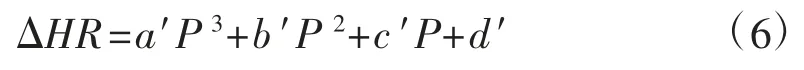
其中，ΔHR 为发电热耗的减少量，kJ/（kW·h）；P为机组当前负荷，kW；a′、b′、c′、d′为多项式系数。

图1、图2 曲线的负荷下限为140 MW，相当于机组40%的额定负荷。此负荷及以下由于烟气温度降低已不能通过锅炉烟气余热利用设备回收余热，因此发电热耗率降低为零。另外，由于燃煤机组锅炉均存在一个最低稳燃负荷，这一负荷往往≥40%额定负荷，机组负荷基本都在40%额定负荷以上工况运行，因此这一曲线可以广泛应用于机组的日常计算当中。

2.3 节能计算中的积分运算

定积分运算是一种求和运算。对于在定义区间［α，β］上有界的函数f（x），在［α，β］中任意插入若干个分点，α＝x0＜x1＜x2＜...＜xn-1＜xn=β，把区间［α，β］分成n 个小区间［x0，x1］，［x1，x2］，…，［xn-1，xn］。当Δx1＝x1－x0，Δx2＝x2－x1，…，Δxn＝xn－xn-1；λ ＝max

对于电厂生产而言，机组的发电负荷P 是一个随时间变化的量，因此可以认为负荷与时间存在以下函数关系

若将式（7）中的x 看作是时间，α、β 分别表示电厂节能量统计的起止时刻，将式（8）代入式（7）则A 即为统计期所发的电能量。

随着计算机技术在电力生产中的应用，电量已完全实现实时统计，而且负荷采样的时间间隔已达到秒级甚至更快，这个间隔远远低于月、季、年的统计时间跨度，因此可以认为统计期所发的电能为

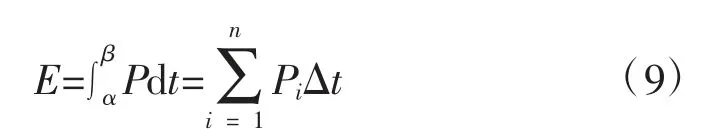
其中，E 为统计期所发的电能量，kJ；n 为采样次数；Δt为采样时间间隔，s。

由于Δt为固定采样间隔，因此式（9）又可以改写为

统计期内的平均电负荷即为

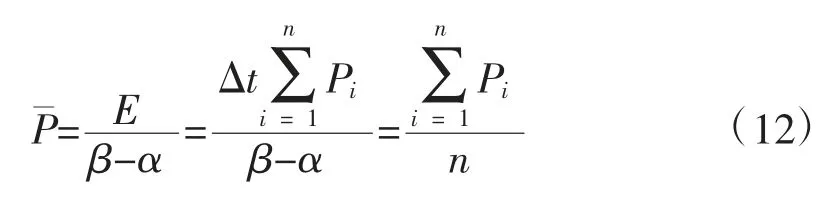
由此可得，机组在统计期内的平均负荷即为统计期内各采样负荷的平均值。

设ΔEt为机组负荷为Pt时的节能量，则

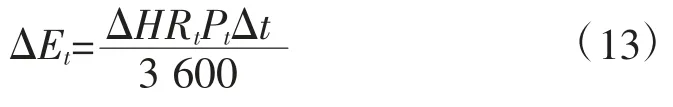
其中，ΔHRt为负荷为Pt时的发电热耗率减少量，kJ/（kW·h）。

由式（16）可得出，在统计期内的平均节能量即为同期平均负荷对应的节能量。也就是说，要想获得某一统计期内与机组负荷有关的节能措施的节能量，只需获得统计期内负荷与节能量的关系曲线，并计算出统计期机组平均负荷，利用平均负荷计算出统计期内单位时间的节能量。利用这一节能量即可获得整个统计期节能量，完全无需分负荷段统计时间和进行加权求解。

机组年节能量计算公式由式（1）变为

对比式（1）和式（17）不难看出，式（17）的计算有效避免了负荷分段统计和加权计算，不仅计算得到有效简化，而且计算中通过有效利用排汽比容拟合有效提高了计算精度。

3 改造机组节能量计算

某350 MW 超临界抽汽供热机组进行了锅炉烟气余热利用改造，汽轮机型号为CCZK350/289.6-24.6/1.5/0.4/569/569，为了获得机组改造节能量，先后测试了阀门全开工况、100%、75%、50%、40%运行工况，其中40%工况点余热利用量为零。表1 为采用不同排汽焓所得机组发电热耗率的变化情况。

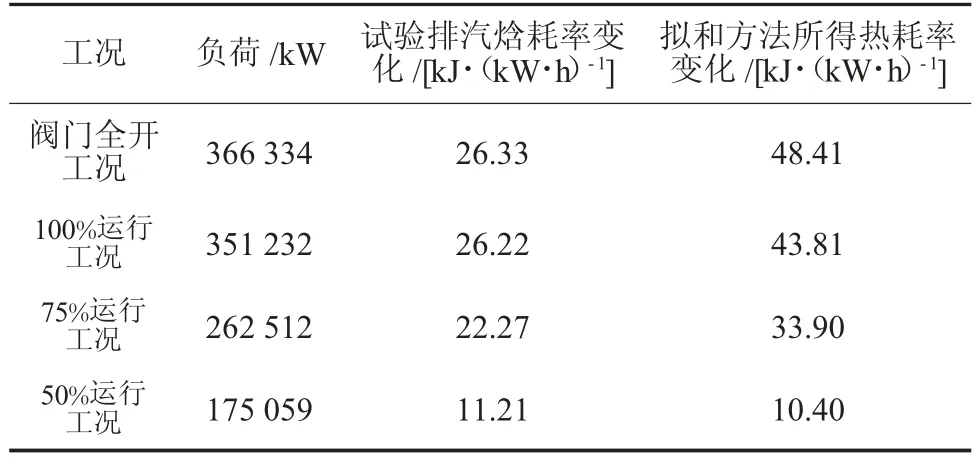
表1 不同方法计算发电热耗率对比

由表1 可以看出，采用不同排汽焓的计算对机组节能量的影响很大，此偏差累计到一个统计周期中将是一个非常大的数值。对机组热耗降低值与负荷关系进行拟合得

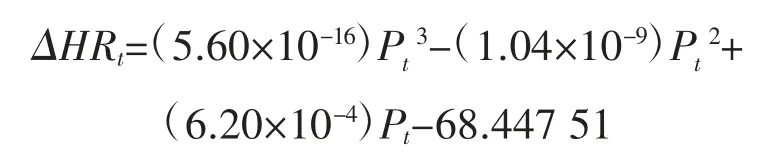
统计机组年利用小时数为6 312 h，平均负荷为280 630 kW，锅炉效率92%，将数据代入式（17）得年节煤量为标准煤2 380.8 t。

4 结论

综上所述，在计算节能量与机组负荷变化相关联的节能措施节能量中，首先是节能量计算将涉及机组变工况的计算，此时机组排汽焓的确定将直接影响最终节能量结果的准确性，通过采用排汽比容拟合方法确定变工况后的机组排汽焓将有效提高计算精度。其次，通过机组发电热耗率与负荷关系的拟合能够有效涵盖机组的全负荷范围，避免了以点代面造成的计算偏差。再次，采用拟合平均法可以有效避免机组按负荷段进行分段统计的繁琐步骤，从而大幅度提高了计算效率，并有利于嵌入计算机系统中实现实时统计计算，能够为机组运行节能分析和优化提供有力支持。最后，拟合计算方法是建立在有效的运行测试基础之上，100%、75%、50%等负荷点工况虽能基本满足节能量的计算要求，但为了能够更准确地反映机组运行状况，在机组具备相应试验条件的情况下建议多设置几个试验负荷点来进一步提高拟合精度。