基于改进粒子群算法的主动配电网有功无功协调优化研究

吴秋兵

（国网太原供电公司，山西太原 030001）

0 引言

作为配电网发展的高级阶段产物，主动配电网技术不仅能够应对分布式电源入网带来的不利影响，因其对可再生能源电网内的有功、无功调节措施，还可以尽可能地降低网络损耗，提高电能质量，实现配电网的经济运行。文献[1]考虑了需求响应和储能的无功优化模型，通过储能的加入优化了系统的电压，提高了分布式电源的接入比例。文献[2]建立了考虑用户需求侧负荷的可调度模型，通过改进免疫算法实现对配电网的优化调度。为了将风电和光伏机组的不确定性加入到优化调度模型中，文献[3-5]计及了分布式电源的不确定性，文献[6-8]建立了基于预测的不确定性多目标优化模型，通过智能算法求解了模型，但对负荷的波动未作考虑。文献[9]建立了以求解网损最小、电压偏差最小、最大可再生分布式电源接入容量为优化模型。而文献[10-12]则从配电网的有功、无功多角度出发，通过对储能、燃气轮机进行优化调度，同时计及无功电压模型，实现了对配电网的无功联合优化。该方法打破传统静态优化方法，将有功与无功协调控制，实现配电网的动态优化，将新能源消纳、无功电压控制及移峰平谷等考虑在内，实现了主动配电网的综合最优调度控制。

1 主动配电网有功无功协调优化模型

1.1 主动配电网有功无功协调优化目标

主动配电网有功无功协调优化通过对分布式发电、储能装置ESS（energy storage system）等的有功功率和无功补偿装置的无功功率的协调控制，实现了主动配电网消纳间歇性分布式能源最大化、网损最小化和电压质量优质的综合优化目标。

综合优化目标函数包含了3 个子目标函数，即在满足电网安全运行的约束条件下，以子目标F1——电网消纳间歇性分布式能源最大、子目标F2——网损、子目标F3——电压偏差最小构成的综合目标函数最优为求解目的，经过归一化处理后的子目标函数F1、F2、F3均无量纲，可将主动配电网优化综合目标函数表示为

其中，ω1、ω2、ω3分别为各目标函数权重系数。理论上讲，不同时间对于不同目标的侧重不一样。

目标函数1（F1）：以促进可再生能源消纳为目标。主动配电网有功无功优化调度应以提升可再生分布式电源消纳比例为首要任务。在不影响电网用电可靠性的前提下，建立以提升可再生分布式电源消纳为目的的优化模型，尽量多消纳分布式电源，使得从主网购置的电量减少。因此，将从主网购置的电量占总用电量最小为目标函数，与以促进可再生能源尽可能消纳为目标具有一致性。

目标函数2（F2）：以配电网的网络损耗最小为目标。在主动配电网中有功无功协调优化调度过程中，将网络损耗最小作为优化目标具有现实意义。通过制定科学合理的调压措施进一步降低网络损耗，可以提升配电网传输功率的效率，优化电网经济指标，对电力系统的安全性也有一定的提升作用。网络损耗计算如下

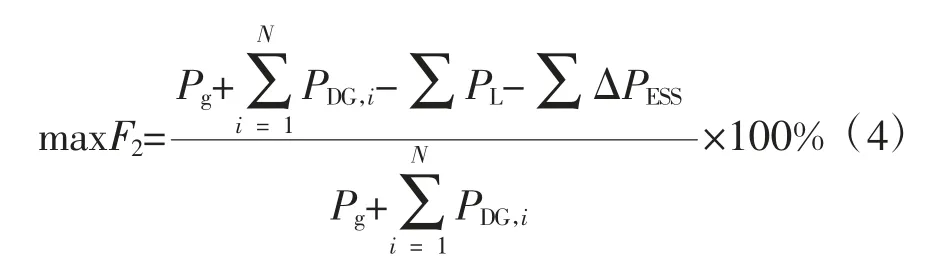
其中，式（4）中的分子部分代表配电网的有功损耗；Pg为主网从根节点传输给配电网络的有功功率；∑PL为配电网络中所有的有功负荷；∑ΔPESS为配电网络中所有电池储能的增量；F2为网络损耗占配电网总有功出力的比例，制定合理的储能充放电策略使得F2最小。

目标函数3（F3）：以电压质量最优为目标。电力系统设备在额定电压下工作时，可以实现最好的工作性能，达到最高的工作效率和预期的使用寿命。因此，需要采取一定的措施使配电网络各节点电压偏移最小。全网节点电压偏移最小的目标函数为

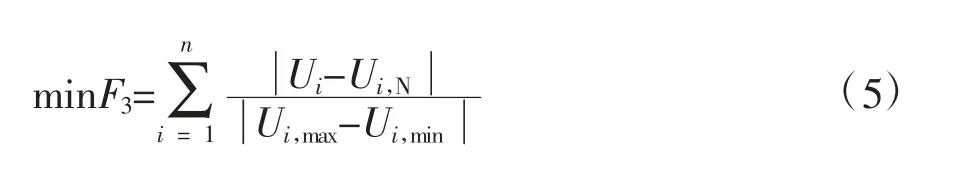
其中，Ui，N为节点的额定电压；Ui为i 节点的实

际测量电压；n 为配电网络中节点个数（包括根节点）；F3为配电网络所有节点电压偏移的平方和，优化目标是使F3最小。

1.2 优化模型的约束条件

1.2.1 有功无功等式约束

在t 时刻，对于节点的有功功率方程数学表达式如下

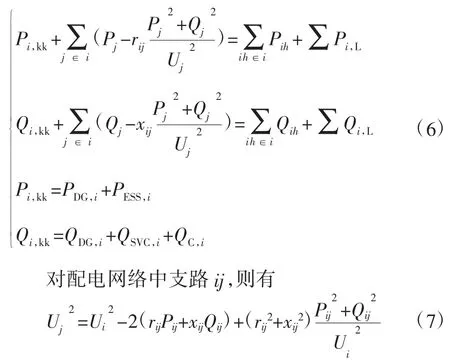
其中，Pi，kk为可控有功功率，包括分布式电源、储能电池从节点i 注入网络的有功功率总和；Qi，kk为可控无功功率，包括分布式电源（DG）、储能电池（ESS）、无功补偿C（capacitors）从i 节点注入网络的无功功率总和；Ui、Uj表示节点i、j 的电压幅值；rij、xij表示节点i、j 的网络阻抗；j∈i 表示节点i 的所有上级节点的集合；ih∈i 表示节点i 的下级支路的集合；Pih表示从节点i 流向下级线路ih 有功功率；∑Pi，L、∑Qi，L表示节点i 的总有功负荷、总无功负荷；Pij、Qij为由节点注入支路的有功功率、无功功率。

1.2.2 主网向配网输送功率约束

主网从根节点向配电系统输送的功率因受电力系统调度制约而有一定的范围，超出这个范围，将造成电力系统波动，不利于其稳定运行。t 时刻主网从根节点向配电网输入的功率Pg、Qg范围为

1.2.3 系统中节点电压约束

根据电力系统安全运行要求，系统中节点电压有效值与额定电压相差不能太大，仅允许其在一定范围内波动。t 时刻节点i 的电压波动范围为

其中，Ui，min、Ui，max为节点i 允许电压的最小值、最大值。

1.2.4 系统中支路电流约束

支路电流越大，网络损耗越大，当支路电流超过允许值，将对系统安全运行产生不利影响，因此要对电流有如下约束

1.2.5 分布式电源出力约束

分布式电源受到技术特性和设备本身容量限制，其有功无功出力都只能在一定的范围内实现。

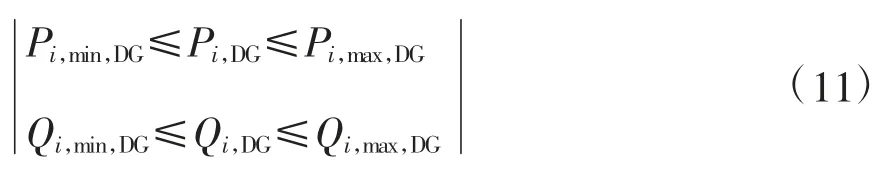
其中，Pi，DG、Qi，DG为t 时刻接在节点上的DG 有功、无功出力；Pi，min，DG、Qi，min，DG为DG 运行时有功出力最小值和最大值；Qi，min，DG、Qi，max，DG为DG 运行时无功出力最小值和最大值；本文DG 采用恒功率因数模型。

1.2.6 储能充放电约束

储能系统既可以充电也可以放电，既可以作为电源也可以作为负荷，在时刻t，对ESS 的运行参量有如下约束[13]

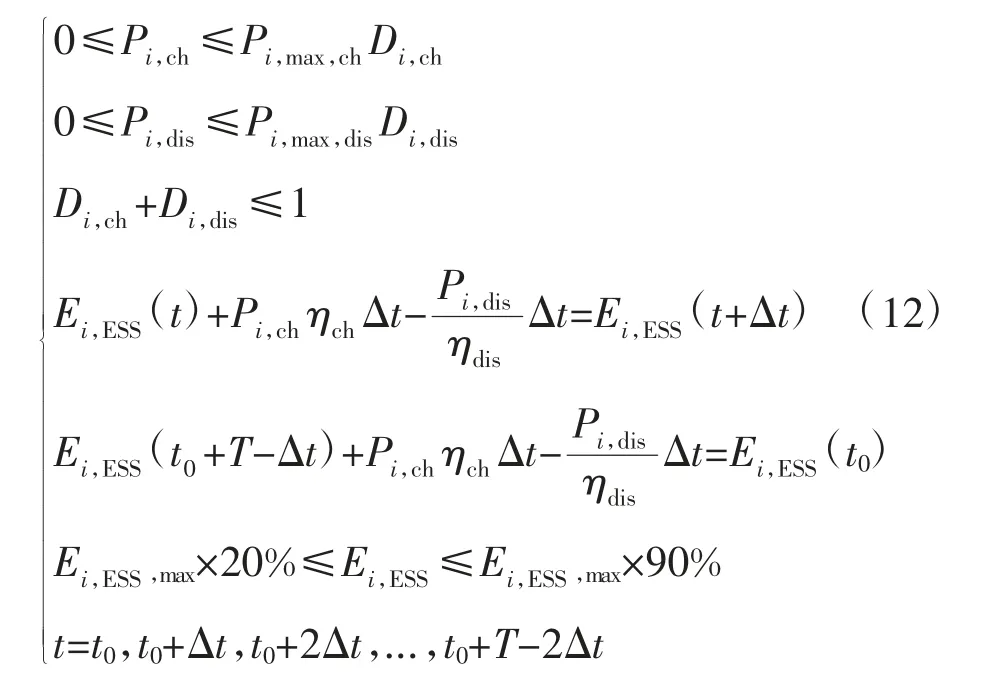
其中，Pi，ch、Pi，dis表示t 时刻节点i 充电、放电功率；Di，ch、Di，dis为t 时刻节点的充放电状态变量，只取0 或1，两者之和小于1 表示t 时刻节点i 处所接ESS 不能同时处于充电和放电状态；Ei，ESS（t）为t时刻节点处所接ESS 电量；Ei，ESS，max为储能容量限值；ηch、ηdis为充电、放电效率；Δt 为调节时间；T 为调节周期；Ei，ESS，max表示ESS 储能容量最大值。

1.2.7 静止无功补偿装置出力约束

静止无功补偿装置SVC（static var compensator）的无功出力可以连续调节，其出力约束为

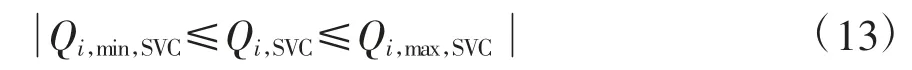
其中，Qi，SVC、Qi，min，SVC、Qi，max，SVC分别为t 时刻i 节点连接的SVC 实际出力、允许出力最小值、允许出力最大值。

1.2.8 电容器组投切约束

电容器组CB（capacitor bank）提供无功功率为离散型，其数学表达式为：

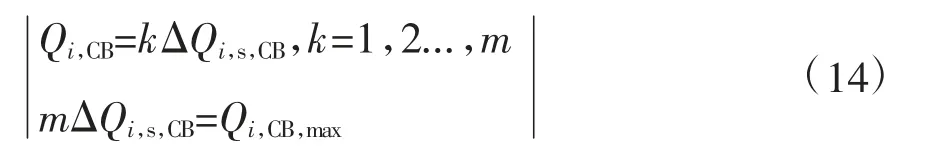
其中，Qi，CB为节点i 连接的CB 在t 时刻从节点i注入的无功功率；Qi，s，CB为每组投切量值；Qi，CB，max为节点连接的电容器组容量的最大值。

2 算法及问题求解

2.1 算法实现

本文采用改进粒子群算法PSO（particle swarm optimization），在原有粒子群算法基础上，引入免疫算法的免疫信息处理机制，把这种多样性和自我调节能力特性引入PSO 算法中，提出了免疫粒子群算法IPSO（immune particle swarm optimization algorithm）对问题的求解，以提高算法的全局搜索能力而不致陷于局部解。IAPSO 算法计算步骤如下。

a）初始化粒子群。随机生成满足所有不等式约束的初始群体，表示含所控制变量的可能取值，并按实数进行编码，以向量u 表示，则ui，j[k]表示进化中的第k 个个体的第j 个控制变量。

因此，第0 代含有N（种群大小）个个体的初始群体，第i 个的第j 个控制变量初始化为

其中，U 为服从均匀分布的随机函数，ujmax和ujmin为第j 个控制变量取值的上下限。

本文将浓度机制引入粒子群适应度计算过程中，以保证粒子群的多样性。

第i 个粒子（抗体）的浓度定义如下

其中，xi和f（xi）分别表示第i 个粒子及其适应度函数。

由式（17）可知，与粒子i 相似的粒子越多，粒子i 被选中的概率越小。反之，与粒子i 相似的粒子越少，粒子i 被选中的概率越大，这使得低适应度个体也可获得进化的机会。

b）初始化免疫疫苗。将免疫疫苗定为全局最优粒子。

c）更新粒子的位置和速度。按照式（18）、式（19）对每个粒子的速度和位置进行更新。

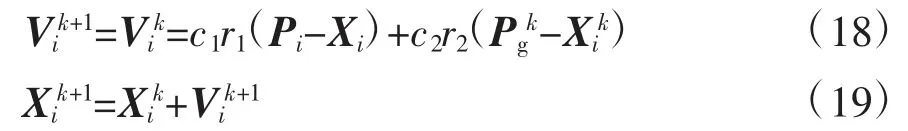
其中，粒子标号可表示成i=1，2，3，．．．，m；k 为迭代代数；c1、c2代表学习因子，一般取值为[1.5，2.05]；r1、r2是均匀分布于[0，1]之间的两个随机数；P 表示粒子群的位置；V 表示迭代速度。

本文采用自适应调节w 的策略，即随迭代次数的增加线性减少

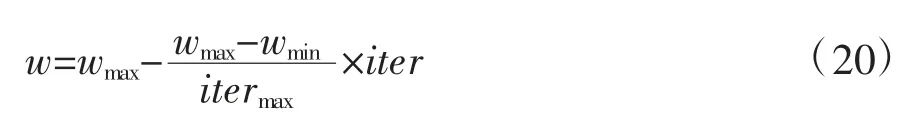
其中，wmax、wmin分别为惯性权值w 的起始值和终止值；itermax、iter 分别为最大迭代次数和当前迭代次数。w 随迭代次数线性减少，实现了搜索空间从全局向局部的过渡，在应用过程中取得了较好的结果。

d）群体的更新。将更新后粒子的适应值与更新前粒子的适应值进行比较，如果适应值增加，则粒子的位置才进行更新，否则保留原来粒子的位置。

e）随机加入M 个新粒子，保持种群多样性。

f）采用轮盘赌策略，选择N 个粒子变异为新的群体。

g）免疫接种和免疫选择。对式（16）产生的免疫疫苗更新R 个粒子，保留优良粒子进入下一代。

h）计算适应度，获取全局最优值。

j）判断是否满足约束条件。如果迭代次数iter大于最大迭代次数itermax，则结束循环输出结果，否则转到步骤b）。

2.2 算法流程

自适应权重的IAPSO 主动配电网有功无功协调优化模型流程如图1 所示。

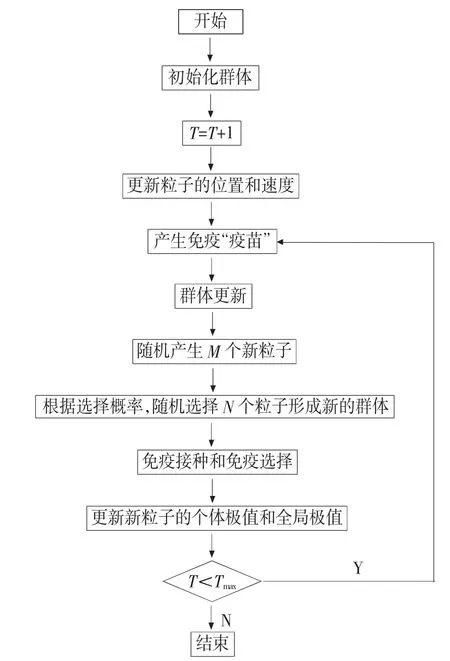
图1 IAPSO 的算法流程图

3 算例计算与结果分析

本文以IEEE33 节点配网（见图2）为基础算例，其中支路参数不做改变。在节点17 处分别接入装机容量400 kW，功率因数恒定为cosφ=0.95 的光伏PV（此处DG 仅考虑光伏PV）；在节点8 接入容量为200 kW 的风电场，功率因数恒定为cosφ=0.98。在节点20 分别接入充放电功率上限为100 kW、总电量上限为1 200 kW·h、充放电效率均为93.81%的储能系统ESS；在节点7 连接调节范围为-100~300 kvar的SVC；在节点10 连接525 kvar 的分组投切电容器C，即每个电容器容量限值为0~125 kvar。所选配电网有32 条支路、33 个节点，基准电压为12.66 kV，基准功率取10 MVA，全网总负荷为5 084.26+j2 547.32 kVA。为贴近实际电网运行特点，采取动态无功优化方法，选取光伏波动范围较大时段11：00—15：00 作为计算周期，取值采样周期为30 min/每次。

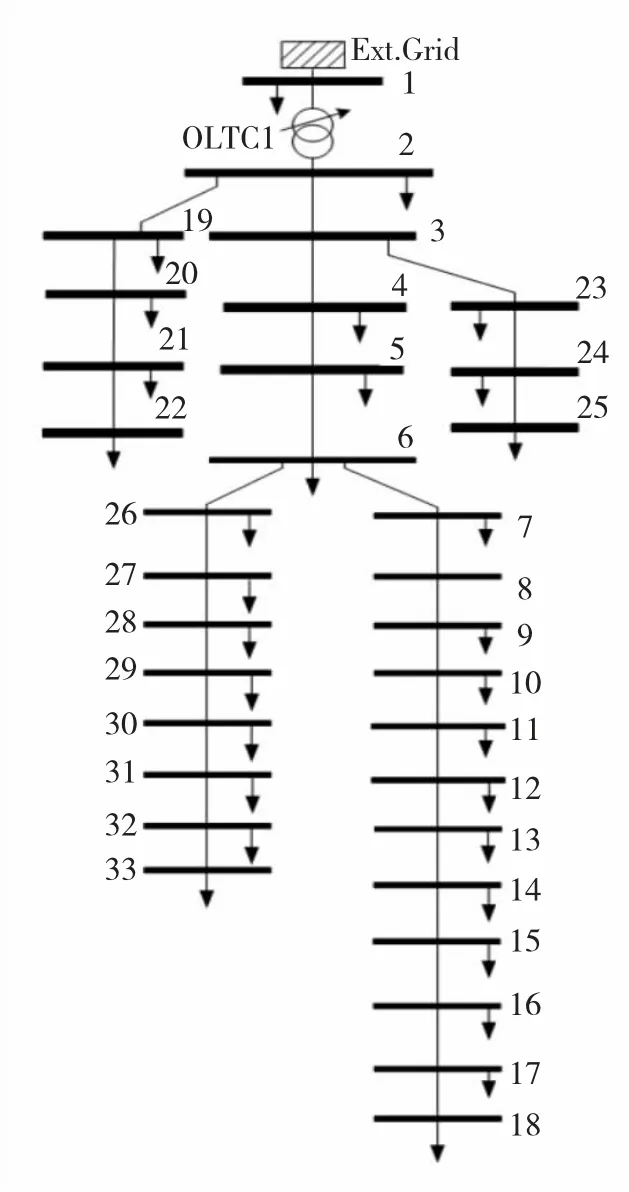
图2 IEEE33 节点配网图

3.1 无功补偿设备对电网网损的影响分析

为研究无功补偿设备对配电网的无功及电压的影响，此处计算24 h 内的无功补偿设备接入对配电网网损的影响，其对比结果如图3 所示。

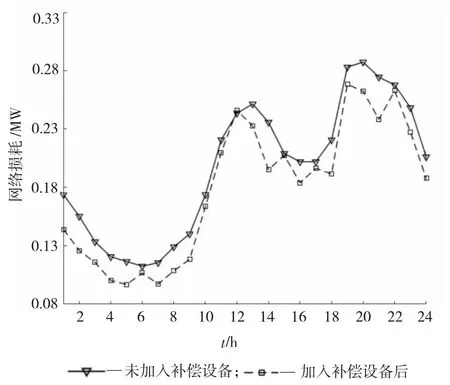
图3 无功补偿设备接入对配电网网损的影响

图3 计算结果表明，无功补偿设备的接入对配电网的网损有明显降低的作用，这是因配电网末端无无功电源，此时加入无功补偿装置提高了系统无功容量，提升了网络功率输送效率。

3.2 无功补偿设备对含分布式电源配电网的电压影响分析

在节点17 接入容量为400 kW 的光伏电站，同时将容量为150 kW 的风电场并入节点8，分别计算的无功补偿设备接入前后系统的电压值变化如图4 所示。

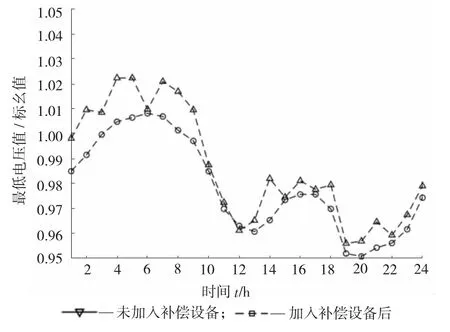
图4 无功补偿设备接入对含DG 配电网电压的影响

图4 计算结果表明，无功补偿设备的接入在很大程度上可以缓解因分布式电源接入造成的配电网电压抬升的情况，可将全网电压调整到0.95～1.01标幺值的合理范围内。

3.3 计及电压偏移的有功无功协调优化分析

本文按照基础参数为风电场、光伏电站配置合理的储能装置可以减少系统无功网损，平滑电压波动，减轻调峰压力。将储能单元参与到有功无功优化模型中，通过合理分配储能单元的充放电策略，并且采取动态无功优化策略，选取光伏波动范围较大的11：00—15：00 为计算周期，运用本文所提有功无功协调优化模型对改进算例进行计算。

最终优化结果表明，在计算周期内有功网损为0.198 MW，与图2 优化结果对比，同时段内网损减少0.4 MW，降幅66.7%。节点电压平均偏移值为0.004标幺值，电压稳定性提升46.3%。

通过将储能单元统一参与到配电网有功无功优化调度模型中，利用储能去平滑风光的出力波动，减少电网潮流波动，进而降低配电网网络损耗；同时，由于电网潮流波动减小，有利于SVC 以及电容器的动态调节措施制定，最终使电网的电压稳定性得到提高。

4 结束语

对于高比例的含分布式电源的配电网来说，因为分布式电源出力的随机波动性导致电网潮流及电压的动态调整越来越困难，本文提出基于改进粒子群算法的有功无功协调调度模型，以电网网络损耗和电压稳定性指标为综合优化指标，并在IEEE33节点算例进行了仿真分析，得到以下结论。

a）高接入比例的分布式电源的出力波动性会造成配电网调压困难，使调压设备动作次数越限，不利于配电网的安全稳定运行。

b）为分布式电源配备一定比例的储能装置有利于降低弃风弃光率，还能缓解电网调峰压力，平滑分布式电源出力曲线，有利于电网制定合理的无功优化策略。

c）将储能装置参与到含分布式电源的配电网无功优化模型中来协调考虑具有很高的经济性和科学性，有助于提升未来分布式电源高比例接入的配电网的运行可靠性和经济性水平，缓解配电网设备升级的迫切性，有利于电网企业优化能源结构。