分有法，合有道——《分数的意义》教学策略例谈

陈 燕

(江苏省淮安市老坝口小学 江苏 淮安 223001)

1.分有法

1.1 单位“1”教学策略例谈。在之前的学习中，学生已经陆续了解到可以将一个物体平均分，也可以将一些物体组成的整体平均分。尽管如此，单位“1”的认识对学生来说仍是有距离感且不易理解的。因此，如何将单位“1”的概念抽象出来，是教师急需要解决的问题。

(1)策略一：从1到“1”，巧识单位“1”

出示：一个月饼，一张白纸，一把1米长的尺子

师：都可以用自然数几来表示？生：1

师：你认为自然数1还可以表示什么？生：一个整体

师：(抓起一把粉笔)能用1表示吗？生：1把粉笔

师：(一叠白纸)，能用1表示吗？生：1叠白纸

师：(出示12条金鱼，99朵玫瑰， 40分钟)……

生：一群金鱼、一束玫瑰、一节课……

师：现在你对1又有了什么认识？

生：1可以表示一个物体、一个整体、一个计量单位……

师：像这样的一个物体、一个整体、一个计量单位都可以看作为单位“1”。

师：1上面为什么加引号？

生：说明这里的1并不仅仅是一个物体，也有可能是许多物体组成的一个整体……

师：单位“1”还可以表示什么？现在你可以把什么看作单位“1”？

在这一段的教学中，教者能从1入手，先让学生用1来描述相关事物，如1个物体、1个整体、1节课、1把粉笔等等，让学生在描述中体会到无论是1个物体，还是由许多物体，都可以用1来表示，扩大了1的范围；接着将学生认识到的这些1抽象概括成单位“1”，并通过1和“1”的对比让学生明确，单位“1”不同于1，是因为其有着更为丰富的内涵：它不仅仅可以表示1个物体，更可以表示其它内容。而1与“1”的对比，则让学生进一步明确了它们的异同，让学生在对比中明确：“1”并不是真正的1，因为其所指向的对象更为丰富，数量上也突破了1的局限性。

(2)策略二：从分到合，分出单位“1”

单位“1”所能概括的事物非常广泛，教材中给出了一个物体、一个计量单位、一个整体的例举。对学生来说，学生所认识的单位“1”则更为详细具体，比如一个苹果、一盘桃子、一张纸、一瓶水等等，这些事物往往都非常详细、具体。而分类，可以很好的帮助学生从这些具体的事物中概括总结出普遍性规律，有助于学生归纳形成对单位“1”的认识。

师：出示四幅图，你能用分数表示图中涂色部分吗？

同桌互相说一说。

指名两人板演并说一说每个分数的含义。

师：你能依次说一说这几个分数分别是将什么平均分呢？

学生口答，教师根据口答板贴均分事物的图片。

师：你能将这些对象分分类吗？

学生尝试将黑板中的图片分分类。

根据学生分类情况依次总结：一个物体、一个计量单位、一个整体

师：如果让你用一个字来表示，你想到了什么？

生：1

师：像这样的一个物体、一个计量单位、一个整体，都可以看作是单位“1”。

师：为什么1要加双引号?生活中还有什么可以看作单位“1”？

单位“1”有着极其丰富的内涵，如何让学生认识并理解这样的内涵呢？教者分成了这样的两个层次：首先，出示丰富的素材，让学生根据图片说一说各可以用哪个分数表示，以及这个分数的具体含义。直观的图片为学生认识其丰富性提供了可能，让学生在观察、讨论、交流中明晰不同的分数是将不同的事物进行平均分；其次，教者将上述均分的物体展现出来，引导学生将他们分分类。让学生在分类比较的过程中进一步体会单位“1”的丰富性，并且顺理成章地概括出“一个物体、一个计量单位、一个整体”，在这样的概括的过程中掌握单位“1”的含义。

策略三：以退为进，猜出单位“1”

师：出示四分之三，说一说表示什么意思？

问：四分之三可以把什么平均分？

学生口答：一个苹果、一个月饼、一块蛋糕……

师：一个盒子，里面装着想平均分的物体，猜一猜是什么？

根据学生猜测依次出示一个月饼，一个长方形，一个1米线段，8个苹果等。

师：(指着8个苹果)这还是一个物体吗？

介绍：一个整体

师：还可以将什么平均分？

学生口答：一个班的学生、一筐苹果……

该策略充分利用学生已有的认知经验，让学生从熟悉的分数“四分之三”入手，先说一说它的含义，再推想“四分之三”可以将哪些物体平均分？学生在交流的过程中会突破思维的局限性，如根据“一盘桃子”可以联想到“一篮桃子”、“一筐桃子”、“一车桃子”等等，这样的联想是可贵的，让学生充分体会到单位“1”表述事物的广泛性。接着教者又进一步拓展延伸，提出问题：“还可以将什么平均分？”在学生在群体交流中进一步体会单位“1”包含事物的广泛性。

2.合有道

2.1 借助数轴图，巧妙识分数。分数是数的世界中不可或缺的一部分。对五年级的学生来说，学生并非初识分数，也并非初识数轴图。之前认识小数、正数和负数时，就曾借助于数轴图来认识。数轴图可以帮助学生找准数与点之间的对应关系。借助数轴图来认识分数，不但可以帮助学生更好地理解分数的意义，还可以让学生对数的构成有更为清晰的认识。但是，如何让学生理解并接受相对抽象的数轴图呢？

策略一：分层认识数轴图

数轴是由原点、单位长度、方向(一般规定向右为正)组成的直线。在数轴上，一个单位长度即对应分数意义中的单位“1”，这样的对应关系对学生来说是有着一定的难度的。因此教者可采取分层推进的方法，将数轴图进行分解，这样学生的理解就会变得容易得多。

师：出示数轴图，标注出一个单位长度。

学生理解并回答：这样的一个单位长度表示单位“1”。

继续出示同样单位长度的线段两段、三段……

学生理解并回答：两个单位长度表示2，三个单位长度表示3……

多媒体演示，将若干个单位长度的线段连接起来，填上原点和方向，形成数轴图。

要求学生依次在数轴图上找一找分数，并说明自己的原因。

在上述教学环节中，教者先是从一个单位长度的线段入手，将学生将一个单位长度和单位“1”相对应，明确将一个单位长度的线段均分成几份，其中的一份或几份就表示几分之一或几分之一。这实际上也是对真分数的认识过程；接着，教者突破了学生认识局限，从一个单位长度到几个单位长度，并结合多媒体将数轴图的形成过程展现了出来，让学生体会到无论对应的份数是多少，其均分的份数仍以一个单位长度为标准，这实则也是对假分数和带分数进行了初步的渗透。让学生在分层的认识中亲历了数轴图形成的过程和真、假分数形成的过程，既突出了数轴图表示数据的特点，又帮助学生深化理解了分数的意义。

策略二：分段认识数轴图

出示数轴图，标注出若干个单位长度。

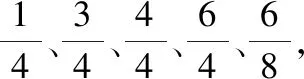
展示数轴图及学生标注的分数。

师：观察这些分数及对应的点，说一说你有什么发现？

生：前几个分数的分母一样，它们都表示把单位“1”平均分成4份；最后一个分数表示把单位“1”平均分成8份。平均分的份数不同，分母也就不同；

生2：表示把单位“1”平均分成4份，表示这样1份的数；其它的分数依次表示这样的3份、4份和6份；

师：说一说它们分别在数字几和几之间？你是怎么理解的？

生：依次说明。

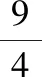
数轴图上，每一段所表示的数据的大小是完全不同的。在上述教学环节中，教者采取分段认识数轴图的方式，先引导学生认识了0与1这一段之间的分数，再逐步引申到其他分数。分段认识的方式让学生对分母和分子所表示的意义有了更深刻的认识，也初步渗透了真、假分数及分数与整数、带分数互化的初步知识，为学生的后续学习奠定基础。

分数之所以叫做分数，是因为其是由“分”而来，3000多年前，古埃及为了在不能分得整数的情况下表示数，用特殊符号表示分子为1的分数。2000多年前，中国有了分数，但是，秦汉时期的分数的表现形式跟现在不一样。后来，印度出现了和我国相似的分数表示法。再往后，阿拉伯人发明了分数线，今天分数的表示法就由此而来。分数是度量和数学本身的需要——除法运算的需要而产生的。让学生更好地理解分数的意义，必须让学生亲历“分”和“取”的过程，“分之有法，取之有道”，在“分-合”的过程中理解分数的本质，才能让学生的学习有根有源，有本有章，才能让学习真正立足于学生需求。