不同叶轮型式对旋流泵性能影响的分析研究

王辉，魏清希，史凤霞

（1. 西安泵阀总厂有限公司，西安 710025； 2. 兰州理工大学，兰州 730050）

旋流泵的主要结构特征是整个叶轮退缩在泵体流道后面的泵腔内，叶轮旋转时在叶轮前面的无叶腔内形成贯通流和循环流。贯通流通过叶轮叶片间流道进入泵室而流出，循环流则在无叶腔内循环。由于叶轮后缩于泵体流道的后侧，故泵体流道进水侧有较大的自由通道，无堵塞性能好，适用于输送易于缠绕、盘卷的长纤维、胶粒或含有大量颗粒的固液两相物料。旋流泵效率普遍低于普通离心泵[1-2]，近年来，国内外学者通过大量的试验研究[3-10]和数值模拟分析[11-15]，研究其几何结构参数对泵性能的影响，进而完善旋流泵的理论及设计方法。本文使用5种不同结构型式的叶轮匹配同一泵体，采用流场模拟软件进行模拟仿真计算，对泵的外特性进行模拟分析，得出旋流泵不同结构型式的叶轮对性能影响的变化规律。

1 旋流泵叶轮结构型式定义

如图1 所示，假定旋流泵叶片从进口开始倾斜的斜角用θ 表示，同旋转方向的斜角在θ 前加F，反旋转方向的斜角在θ 前加R。分别在叶片进口处和靠近出口处开始第一段和第二段倾斜，只在进口处倾斜为单斜叶片（R30），进口处和靠近出口处均倾斜为双向斜叶片（R15-F30、R15-F60、R30-F30、R30-F60）。

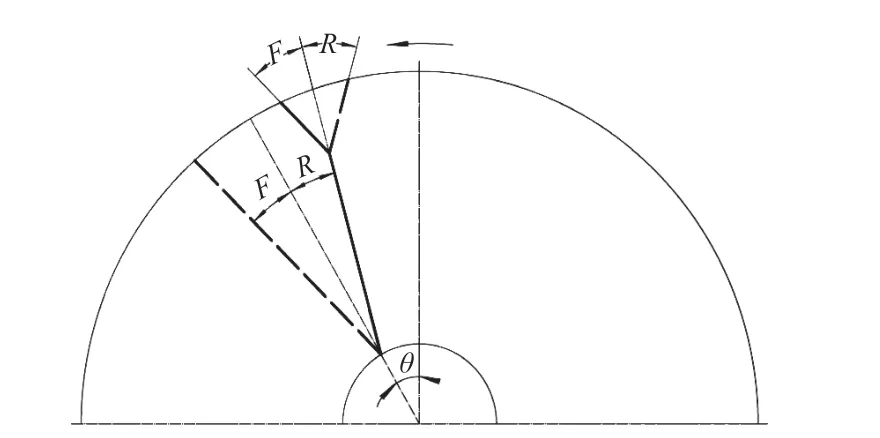
图1 分段双向斜叶片示意Fig.1 Schematic diagram of piecewise bidirectional oblique blade

2 旋流泵内部流场数值模拟

2.1 旋流泵模型建立与网格划分

旋流泵内部流动可认为是复杂的三维不可压湍流流动，是以定常角速度绕固定转轴旋转的旋转流场，对不同方案的模型泵内部流动进行定常模拟数值计算，结合标准к-ε 湍流模型对三维雷诺时均N-S 方程进行求解。

如图2 所示，将内部流动区域划分为进口域（inlet）、转子域（rn）和压出域（outlet）三个区域。采用Simerics MP+内置的基于二叉树算法的笛卡尔网格技术（也称为CAB 算法）对各计算域进行网格划分，为保证计算精度，对转子域和各个交互面进行网格加密设置，设置inlet 最大网格控制精度0.005，rn 和outlet 最大网格控制精度0.002，最终划分网格总数20 171 475。

2.2 边界条件设定

（1）进口边界条件

进口无预旋，切向速度与径向速度为零，进口边界设定为压力条件为P1=101 325 Pa，在进口截面上均匀分布。

（2）出口边界条件

出口选用自由出流条件，边界流动已发展充分，假定在出口截面上满足所有流动变量具有零扩散通量，出口边界设定为流量条件为流量Q。

（3）壁面边界条件

湍流求解在固体壁面上使用无滑移条件，壁面边界条件采用黏性流体无滑移边界，在近固体壁面区域采用壁面函数法。

3 模拟结算结果及分析

3.1 不同叶轮型式的H-Q关系分析

图3 为不同结构型式叶轮的H-Q 模拟结果，可以看出：当流量超过某一值时，旋流泵扬程出现陡降；R15-F60、R30-F60 两种叶轮型式的扬程陡降转折点流量几乎一致，为65 m3/ h；R15-F30、R30-F30 两种叶轮型式的扬程陡降转折点流量几乎一致，为75 m3/h；R30 叶轮的扬程陡降转折点对应流量为70 m3/h；R-F 型式叶轮，当R 一定时，随着F 的增大，泵扬程增加（扬程：R15-F60 ＞R15-F30，R30-F60 ＞R30-F30）；

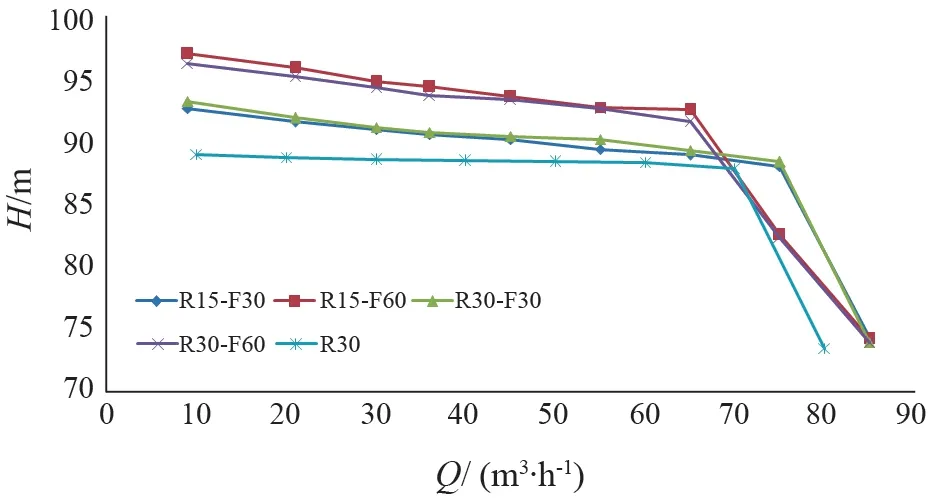
图3 不同叶轮型式的H-Q 曲线Fig.3 H-Q curves of different impeller types

3.2 不同叶轮型式的η-Q关系分析

图4 为不同结构型式叶轮的η-Q 模拟结果，可以看出：R30、R15-F60 和R30-F60 三种叶轮型式最佳效率点流量几乎一致，为65 m3/h，且R15-F60 叶轮的效率整体优于R30-F60；R15-F30 和R30-F30 两种叶轮型式最佳效率点流量几乎一致，为75 m3/h，且R30-F30 叶轮的效率整体优于R15-F30；R30-F30表现出最佳的水力性能，为最佳叶轮型式。

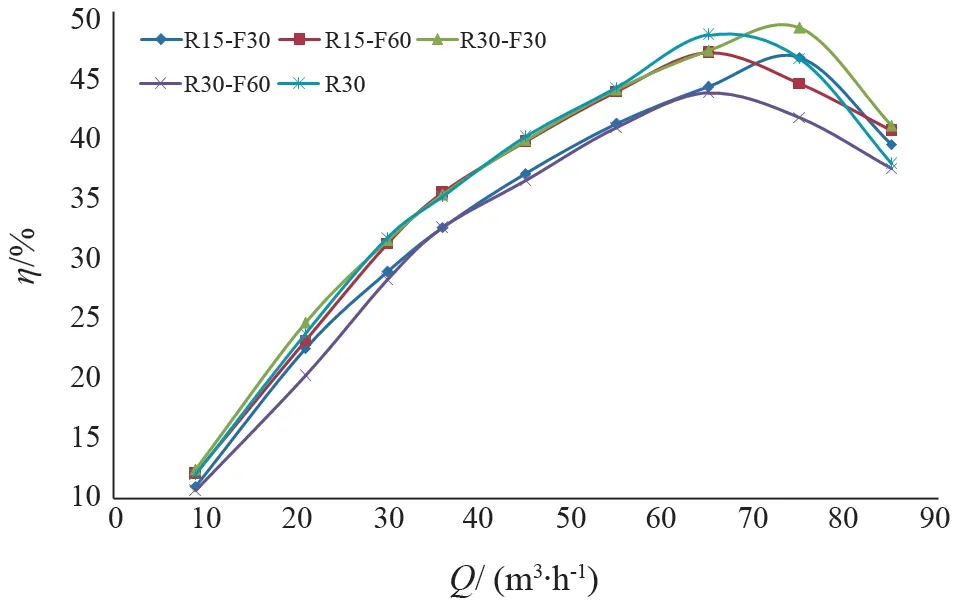
图4 不同叶轮型式的η-Q 曲线Fig.4 η-Q curves of different impeller types

4 结论

（1）当流量大于最佳效率点流量时，旋流泵扬程会发生陡降。

（2）R-F 型式叶轮，当R 一定时，随着F 的增大，泵扬程增加。

（3）当R=15 时，随着F 的增大，其效率明显提高，且高效点向小流量偏移。

（4）当R=30 时，随着F 的增大，其效率明显降低，且高效点向小流量偏移。

（5）R30 型式的单斜叶片，扬程最低，其效率在最佳效率点流量前几乎与R30-F30 一致，流量大于最佳效率点流量后，其效率明显降低；

（6）R30-F30 型式的双向斜叶片表现出的外特性整体优于其他叶轮型式，为最佳叶轮结构型式。