含混合间隙的登机桥动力学分析 *

罗良清，谭朝阳，顾晓勤

(1.灏博生态科技(广东)有限公司，广东 中山 528400; 2.电子科技大学 中山学院，广东 中山 528402)

0 引 言

旅客登机桥是广泛应用于各大航空机场的辅助设备，它是连接候机楼和飞机机身的一种桥梁设备。登机桥系统是一个复杂的多体系统，在一般的多体系统动力学研究中，认为运动关节是理想运动副[1]。然而在实际加工、装配以及工作过程中的磨损、变形，均会造成登机桥运动副的间歇。间隙引起的关节元素之间的接触碰撞，引起了系统的振动和噪声，减小了系统的寿命[2]。间隙会影响登机桥系统的工作性能。为了得到更精确的计算结果，需要考虑运动副间隙对机械系统动力学特性的影响[3]。

笔者针对旅客登机桥系统建立多体系统运动学模型，即10个运动物体，7个相对旋转自由度和3个滑移自由度，对登机桥转动运动副和移动运动副的间歇进行力学分析，得出含混合间隙的登机桥动力学运动方程，最后对某型号登机桥的二种工况进行计算。上述工作对研发新一代登机桥有指导意义。

1 登机桥运动学模型

登机桥按通道个数分为两通道式和三通道式见图1所示，包括支撑立柱、旋转平台、活动通道、接机口、升降立柱、行走系统、以及服务梯，共7部分组成。其中行走系统驱动旅客登机桥实现伸展和收缩，以及水平旋转运动，升降系统提供旅客登机桥在竖直平面的旋转运动。加上电缆输送装置、控制系统和安全辅助系统等，具有自动减速和触机停止功能。当登机桥与飞机接近时，能自动减速。当其与飞机接触时，能自动停止运动。

图1 登机桥系统

三通道登机桥，如图1(c)所示，从内到外分为通道A、通道B、通道C三部分，内外通道之间通过滚轮或者滑块在钢轨道上滚动或滑行，实现伸缩运动，通道B移动速度为通道C的一半。一般通道的顶部与底部为折弯钢板，左右两侧由桁架、玻璃或者钢板组成。

采用多体系统运动学记法[1]，刚体Bi，连体坐标系xiyizi，i=0，1，2，…，10。固定在地面的旋转平台基座B0，旋转平台为B1，如图2所示。

图2 登机桥运动学模型

活动通道A为B2，通道A地板面的根部通过两个铰轴与旋转平台B1相连接，可绕图2中z1轴旋转，从而实现通道随立柱升降。通道B记为B3，与通道A即B2之间沿x2方向滑移。接机平台与通道C连接，通道C与升降机构外立柱的框架用高强度摩擦型螺栓连接成一体，记为B4。升降机构的内立柱固定在行走系统横梁上，记为B5，位于立柱中间的液压油缸的动力推杆伸缩实现整个通道的升降，即内、外立柱沿y4方向平行移动，圆筒型转轴B6与行走系统横梁沿y5方向相对旋转。驱动轮的轮轴B7与B6沿x6方向相对旋转。驱动轮B8、B9各自有一个电机驱动，沿z7轴转动，实现登机桥进退和旋转。接机平台、接机口记为B10，相对B4沿y4′方向旋转，实现与飞机舱门准确对接。图3～5给出了部件之间的联接。

图3 支撑立柱、旋转平台、活动通道联接 图4 活动通道与升降系统

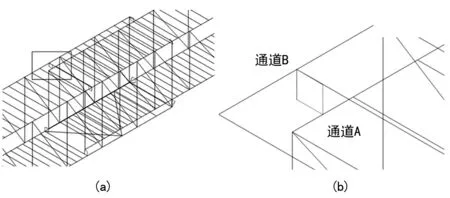
图5 活动通道之间的联接

登机桥系统11个刚体Bi(i=0,1,2,…,10)，相对前一个刚体均为1个自由度运动，即：

B2相对B1：沿z1轴转动θ2;B7相对B6：沿x6轴转动θ7。

B3相对B2：沿x2轴滑移x3;B8相对B7：沿z7轴转动θ8。

B4相对B3：沿x2轴、x3轴滑移x4;B9相对B7：沿z7轴转动θ9。

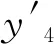
2 旋转间隙分析

行业与企业的可持续发展离不开绿色环保，领军企业更应身先士卒，有所担当。凤凰新华印务以此为行动指南，率先制定企业绿色环保发展战略，全力打造全绿色环境下的印刷工程建设，并严格执行。在绿色环保的探索道路上，凤凰新华印务心怀大局，志存高远，致力于推动整个印刷行业的绿色生态建设。

图6 间隙旋转副

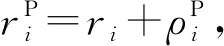
当轴和轴承发生碰撞时，发生动量交换，偏心斜碰撞，在碰撞面处产生碰撞力，将碰撞力分别向法向ni和切向ti投影，导致法向挤压变形的法向力[2-3]：

(1)

当碰撞过程中存在相对切向运动时，会在接触面上产生摩擦力，引起切向畸变。根据库伦摩擦力法则，切向力Ft可表示为:

(2)

式中：μ为摩擦系数，动态校正系数：

v0和v1为切向速度的二个阈值。

Mi=(xPi-xCi)Ft-(yPi-yCi)FN

(3)

同理Mj=(xPj-xCj)Ft-(yPj-yCj)FN

(4)

3 移动间隙分析

移动副间隙接触状态有四种见图7所示[5]：①自由状态，滑块与导槽无接触；②滑块一角与导槽接触；③两个对角同时接触导槽；④侧面全接触状态。

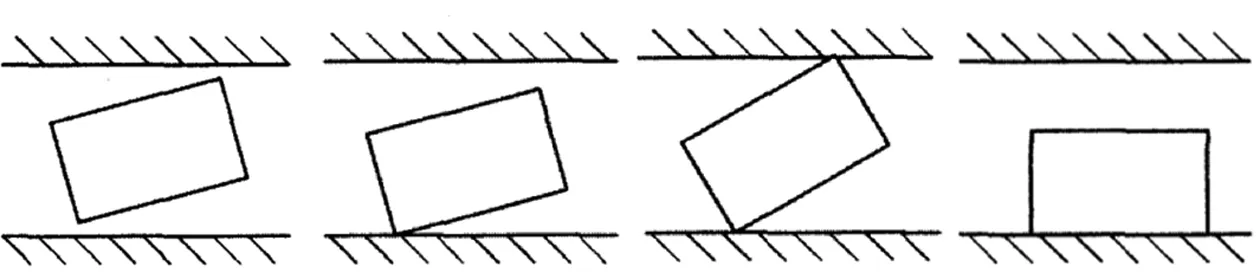
图7 移动副不同运动状态

登机桥通道之间的滑移移动副见图8所示，由滚轮组成，登机桥设计中，B4即通道C的滑动位移、滑动速度为通道B的2倍。

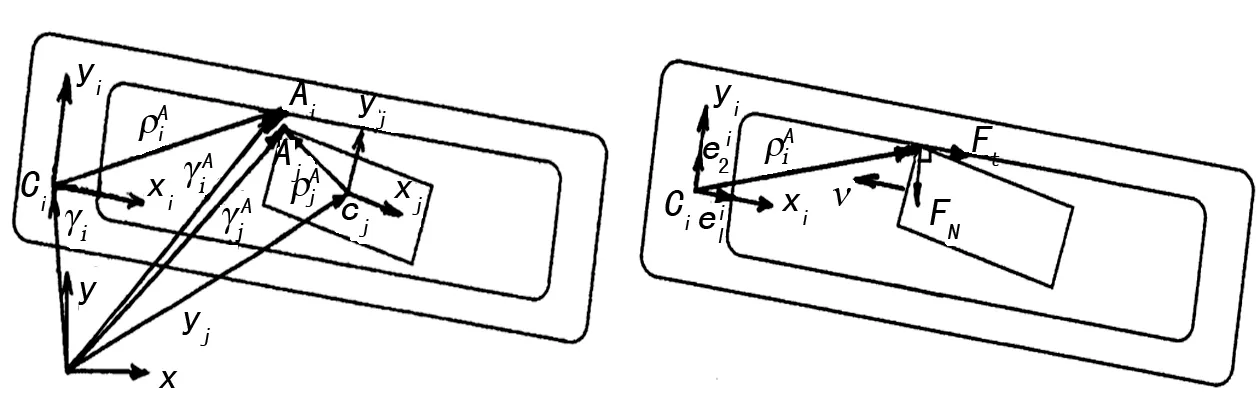
图8 间隙移动副

(5)

式中：a是矩形接触面周长；vi为泊松比；Ei为弹性模量。FN沿yi方向。

(6)

同理斜碰撞力对导槽质心Ci的碰撞力矩:

(7)

4 动力学方程

设绕z1轴转动副有间隙，通道A、B之间存在移动间隙，根据登机桥的位形坐标写出位置约束方程φ(q,t)=0，q=[θ1;θ2;x3;x4;y5;θ6;θ7;θ8;θ9;θ10]T。对时间t求二阶导数得：

(8)

式中：φq为约束方程对广义坐标的Jacobian矩阵。采用拉格朗日方法，建立存在间隙的含约束的多体系统动力学方程为:

(9)

式中：M为系统质量矩阵；Q为系统广义外力，包括系统的摩擦力、间隙碰撞力、重力和外载荷，拉格朗日乘子矢量λ为对应关节的约束反力。

5 运算求解

某型号登机桥通道A质量M2=8 534 kg，通道B质量M3=7 941 kg，通道C与升降系统外立柱质量M4=9 839 kg，接机平台及接机口质量M10=1 952 kg，二者质心距离G4G10=10.37m，行走系统及升降系统内立柱质量2 521 kg，与通道C接触点H。驱动轮直径1.12 m。设初始状态θ20=-50，A1G2=8.72 m，A1G3=21.36 m，A1G4=35.12 m，A1H=34.04 m，通道A与固定转台的转动副中心为A1，接机口登机点K到A1距离44.19 m。运动过程中水平方向摩擦阻力416 N。驱动轮与地面滚动摩阻系数18 mm。通道B滑动速度vB=0.5vc。绕z1轴转动的一对轴承套直径132 mm，轴承直径128 mm，钢材杨氏弹性模量212 GPa，泊松比0.31。

情形1：要求工作期间接机口K点上升速度vKy=0.02 m/s，水平伸展速度vKx=0.05 m/s。则登机桥通道C的滑动速度vc=vKxcosθ1+vKysinθ1，得到图9所示升降系统推力变化规律，图10所示驱动力矩变化规律。

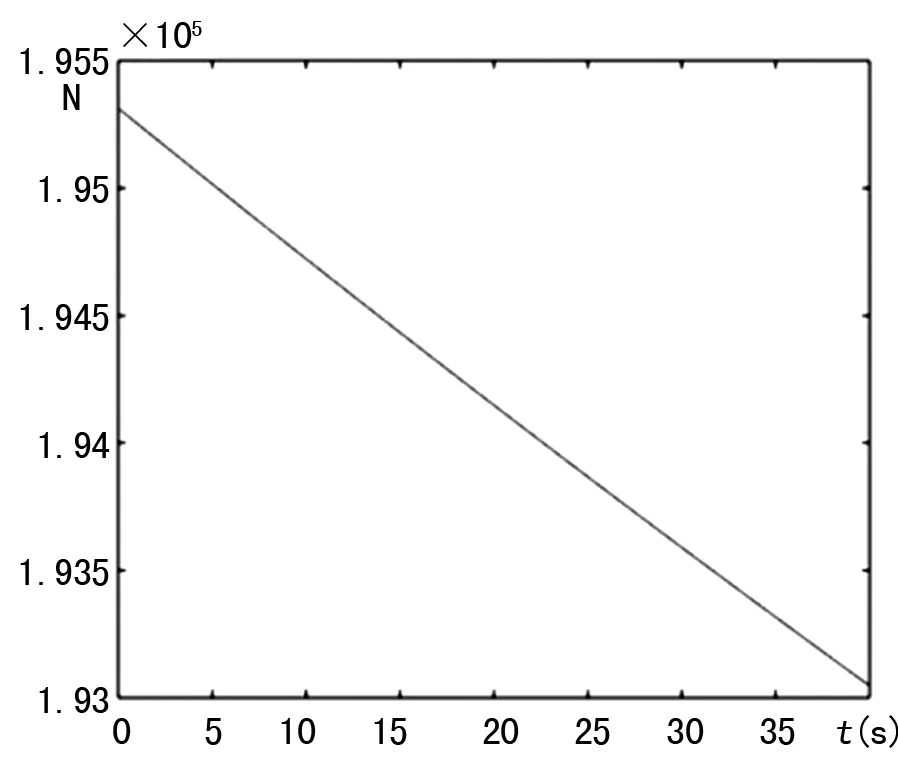
图9 升降系统推力变化规律

情形2：启动阶段4 s，减速停机阶段4 s，通道的角加速度大小均为2.5×10-4rad/s2，驱动轮使通道C产生启动、减速的加速度均为2×10-2m/s2，匀速工作时间32 s。得到图11所示升降系统推力变化规律，图12所示驱动力矩变化规律, 图13所示水平方向驱动力与地面正压力比值变化规律。

图10 驱动力矩变化规律

图11 升降系统推力变化规律

图12 驱动力矩变化规律

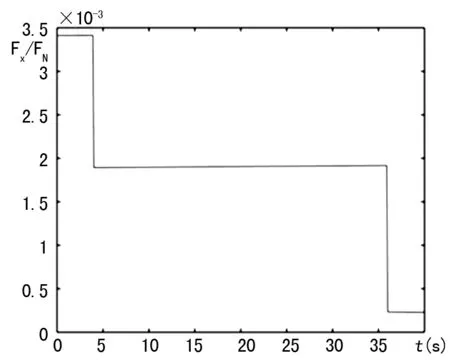
图13 水平方向驱动力与地面正压力比值

6 结 语

重点研究了登机桥系统动力学问题，考虑到登机桥运动副的间歇，引起的关节元素之间的接触碰撞，造成系统的振动和噪声，影响登机桥系统的工作性能。文中首先建立登机桥运动学模型，将系统分为基座加10个运动物体，具有7个旋转自由度和3个滑移自由度，对登机桥转动运动副和移动运动副的间歇进行力学分析，建立含混合间隙的登机桥动力学运动方程。对特定型号的登机桥进行了实际计算。

文中采用多体系统动力学的方法，分析计算机场旅客登机桥系统。对登机桥的细化设计计算有较高的实用价值，对今后登机桥设计有指导意义。

由于登机桥对接、撤离飞机舱门期间属于运动机械，旅客上下飞机期间属于结构物，锚定时候可能碰到台风、大雪等极端天气，所以工作环境复杂，对登机桥安全性、使用寿命、机电系统可靠性等很多方面还有待深入研究。