电动汽车湿式双离合变速器换挡动力学仿真*
楼振雄 段宇鹏 张云清
(华中科技大学国家企业信息化支撑软件工程技术研究中心,武汉,430074)
引言
近年来,随着电动汽车动力性和经济性等优化目标的提出,以及电机设计的逐步完善,通过电机本身的改良来提高工作效率变得越来越困难,而通过对传动系统的优化来提高效率的方式逐渐被人们所重视[1,2].
双离合变速器(DCT)由于其换挡过程中动力不中断、换挡速度快等优点,在电动车中的应用受到许多研究者的关注[3,4].电机良好的调速特性能够进一步发挥双离合变速器动力无中断,换挡冲击小的特点,可显著提高换挡品质,但是换挡过程中的电机与离合器的协调控制问题是DCT研发中的难题.
在传统燃油汽车中,双离合变速器已经有了广泛的应用和研究[5,6],依据离合器传递转矩机理可分为干式双离合变速器(Dry-type DCT)和湿式双离合变速器(Wet-type DCT),干式双离合变速器传动效率较高,接合速度快,但是发热较严重,且使用寿命较短,而湿式双离合变速器寿命长,可靠性高,但由于腔体内油液的损耗使得效率有所下降.德国大众公司(VW)最早于2003年研发了六速双离合变速器,此后,福特,尼桑,宝马,通用等车企均对双离合变速器投入了研究.电动汽车变速箱中,两速比变速箱相比于单速比变速箱显著提升了电动汽车动力性与经济性,而成本远低于多档速比变速箱,同时,两速比的DCT变速箱去除了同步器结构,简化换挡过程,进一步减小了换挡冲击,是目前电动汽车传动系统的发展趋势.
为实现无冲击换挡,双离合变速器中离合器与电机的协调控制极为重要.借助精确的动力学模型,仿真双离合变速器的换挡过程并优化控制策略.Liu等人[7]提出了一种离合器的标定方法,通过离合器滑移过程中的转速传感器,设置了间接的转矩观测器,对离合器传递转矩的模型进行修正,有助于双离合变速器扭矩的精确控制.
Lu等人[8]将干式双离合器视为一个多体系统,针对其在启动阶段的啮合行为进行数值模拟,提出了一种具有双离合变速器的乘用车传动系统的非线性动力学模型.考察了摩擦功,冲击强度和发动机扭矩,将其引入目标函数.建立发动机的动力学模型,根据发动机在换挡过程中的调速需求,改变节气门开度,实现平稳换挡.
Zhao等人[9-11]进行了用换挡冲击度,滑摩功等指标拟定函数对换挡质量进行描述,提出控制算法优化,分别对换挡和起步过程进行了仿真.提出通过鲁棒性控制策略改善换挡品质,该方法在混动车辆的双离合变速器仿真模型中得到验证[12].为了减小齿隙,发动机转矩波动,传感器噪声以及模型的不确定性等对离合器控制效果的影响,文献[13]进一步提出鲁棒性控制使换挡过程更为稳健,而仿真结果表明,该控制策略有效地协调了换挡过程中动力源与离合器的控制.
然而,这些研究讨论了干式DCT而非湿式DCT,而干式离合器的应用范围受到其使用寿命不长,难以承受恶劣工况等缺点的限制.与之相比湿式离合器在接合期间响应更复杂.干式DCT模型可以简化为在啮合,滑动和脱离状态下的分段函数,而对于湿式DCT,换挡过程中传递转矩随时间的动态响应过程不能被忽略.
Zhang等人[14]考虑滑差转速与接合压力的变化对摩擦因数的影响,以库伦摩擦模型表述离合器结合过程.然而该模型只能表述静态的转矩传递模型 .Kulkarni[15]以 Matlab/Simulink 为仿真平台,引入了有效摩擦面积,搭建了整车的动力学模型和换挡控制逻辑,并研究了换挡时离合器压力分布对输出扭矩的影响,优化了离合器的压力变化曲线,对换挡质量进行了改善.但其采用的模型依然为Coulumb摩擦模型.与湿式离合器的动态转矩传递过程有所差异.
考虑到摩擦片之间的油液的影响,多位研究者[15,16]基于 Patir-Cheng平均流量模型的修正雷诺方程对离合器的接合过程进行了数值模拟,将湿式离合器的接合过程分为挤压油液、混合摩擦、粗糙接触三个阶段,将摩擦片的表面视为G-W微凸体接触模型,以高斯分布、维尔分布等对摩擦片表面进行假设,仿真了湿式离合器接合过程中的震颤问题[17].Berger等人[18]考虑了表面粗糙带沟槽的湿式离合器传递转矩的特性,通过有限元模型进行数值计算,对负载、摩擦材料渗透特性、沟槽宽度等对接合特性的影响进行了分析.胡宏伟[19]建立了湿式离合器滑摩过程摩擦转矩的数学模型,通过仿真分析了摩擦系数斜率、静摩擦系数、传动系统阻尼、刚度以及接合压力波动等参数对离合器抖动的影响,为改善离合器摩擦特性以及传动系统设计提供了参考.但在湿式双离合变速器的建模中,研究者常简化了湿式离合器本身的动态特性[20].
Walker等人[21]为研究离合器控制在换挡过程中的真实响应,建立了离合器液压伺服阀的详细模型.控制算法考虑了离合器转矩,发动机转速和转矩控制,对离合器实际扭矩和发动机期望扭矩的差值变化做了敏感性分析,结果表明,在较高的输入扭矩下,当输入扭矩越大,液压系统离合器扭矩控制的误差也会增大,系统的振动也会增大.在理想的发动机转矩前馈控制下,换挡过程的转矩缺口能够实现最小化.在离合器控制上,采用广义预测算法(AGPC),实现对离合器接合过程的精准控制[22].
在换挡质量的评估中,文献[23]仿真表明发动机转矩的输出波动将会导致长时间的滑摩和较大的换挡冲击,此外,齿轮的间隙,同步器的啮合均会导致换挡过程的非线性.对换挡动态过程的研究高度依赖于动力学模型的准确性.
目前在湿式双离合变速箱的研究中,所建立的转矩模型通常为基础的静态转矩传递模型,无法体现换挡中离合器润滑油运动和离合器摩擦片接触的动态过程,对控制策略的制定产生影响.本文将分别采用湿式离合器油液-摩擦片复合模型和经典的库伦摩擦模型,对离合器结合的动态转矩传递过程建模,将其集成到整车的纵向动力学模型中,参照文献[24]换挡过程中电机转矩和离合器压力的控制策略,采用开环控制对换挡过程中的离合器和电机控制进行协调.仿真并分析两种模型下控制效果的差异.
1 换挡动力学模型
DCT换挡过程本质上是电机的输出转矩由原接合离合器平顺转移至原分离离合器的切换过程.湿式离合器模型是传动系统建模的核心部分,其转矩传递的特性直接影响了换挡过程的转矩输出.湿式离合器的接合/分离过程涉及到粘性油液的剪切、挤压以及微凸体的接触,是一个值得研究的耦合问题.同时,动力系统各部件的转动惯量、传动效率也会对换挡时间和换挡质量产生影响.
1.1 湿式离合器转矩传递理论
离合器压紧过程需要克服液压力和摩擦片接合压力,对应的传递转矩由液压油的粘性扭矩和摩擦片的摩擦扭矩共同承担.根据传递转矩的组成,该接合过程可以划分为三个阶段:挤压油液阶段、混合摩擦阶段、粗糙接触阶段.
在离合器接合初期,摩擦片并未产生接触,内部填充有一定粘度的油液.当离合器输入输出存在转速差时,油液产生黏性力,此时传递转矩均由油液内部黏性力贡献.
随着离合器的逐渐接合,摩擦片开始产生局部接触,且接触间隙间依然被油液填充.此时摩擦片的接触和油液的黏性力共同承担离合器传递转矩.
随着离合器接合,摩擦片接触产生的摩擦力逐渐占据主导地位,离合器两侧逐步压紧.当润滑油无法形成油膜时,黏性力可以忽略不计,扭矩传递完全由机械接触的摩擦力承担.
当转速差为零时,离合器完全接合.下文中,将分别对这三个阶段做出理论分析.
1.2 挤压油液阶段
挤压油液阶段,摩擦片尚未接触,转矩传递由液压油黏性力承担.由于湿式离合器较为优良的散热特性,油液在工作过程中状态变化较小,忽略油液密度、黏度等参数的变化,离合器间的油液可以视为较为理想的流体.
根据雷诺数的计算:

其中,ρ为液体密度,v为离合器摩擦副边界液体的相对流速,d为离合器内间隙,μ为动力粘度.估算可得,Re<<2000,摩擦副间可视为层流.流体内摩擦力及剪切应力可以表示为

将离合器假设为内径r1,外径r2的圆环,积分后剪切扭矩为:

该公式未考虑离合间隙d的变化过程带来的影响,故对以上剪切扭矩的表达式进行修正.取接合过程中某微单元液体进行受力分析,根据微元体在离合器圆盘径向方向上的受力平衡,即:
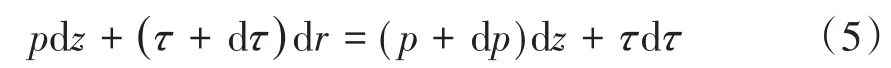
其中,p为微元体位置处油压,τ为剪切应力,r为微元体位置处半径,z为微元体在离合器内部的轴向位置.又根据牛顿内摩擦定律:

联立式(5),式(6)能够得到油膜压力与液体内部流速的关系式:

考虑离合器两侧边界处油液径向速度可视为零,对上式积分得到:

离合器润滑油流量Q为:

代入得到:

对润滑油液做连续介质假设,即x y z三向流量之和守恒,并依据动量守恒定律方程,可以得到挤压阶段油液压力的表达式:

其中u1,u2为小液块x向速度,v1,v2为小液块y向速度,w1,w2为小液块z向速度.h为摩擦副中的油膜厚度,ħ为摩擦副的平均间隙.考虑到各向流量因数ϕx,ϕy,ϕs及联合粗糙度σ,摩擦片渗透系数φ,修正后得到平均雷诺方程:

流量因数ϕx,ϕy,ϕs通过Patir-Cheng[15]总结的计算公式得到.将上式表示为圆形离合器中的压力随径向分布的形式,并将油压p在径向积分得到:
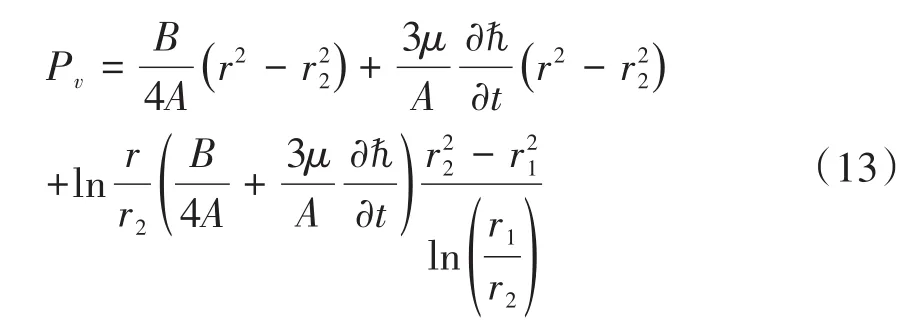
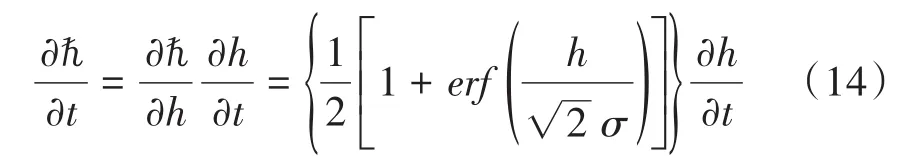
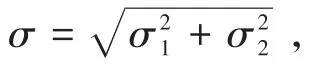

整理得到第一阶段挤压油液过程的润滑油压力表达式:
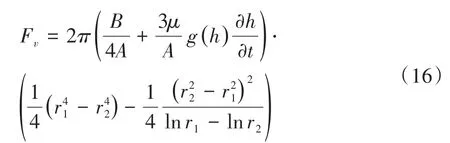
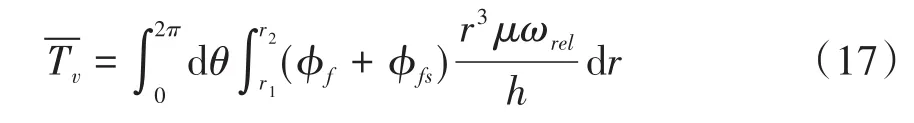
1.3 混合摩擦阶段
当离合器油膜厚度逐渐减小,离合器摩擦片微凸体部分开始接触,发生弹性或塑性形变,产生摩擦转矩和压力.此时,离合器作动器的压力与油压、接触正压力平衡,离合器传递转矩为油液剪切转矩和摩擦片接触摩擦转矩之和.
根据摩擦学中粗糙表面弹塑性接触的有效面积公式得到:
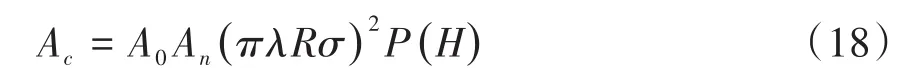
其中,P(H)表示摩擦片微凸体高度大于H,即发生接触部分的概率密度
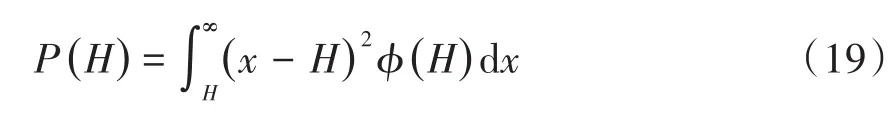
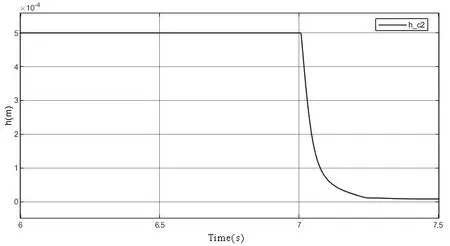
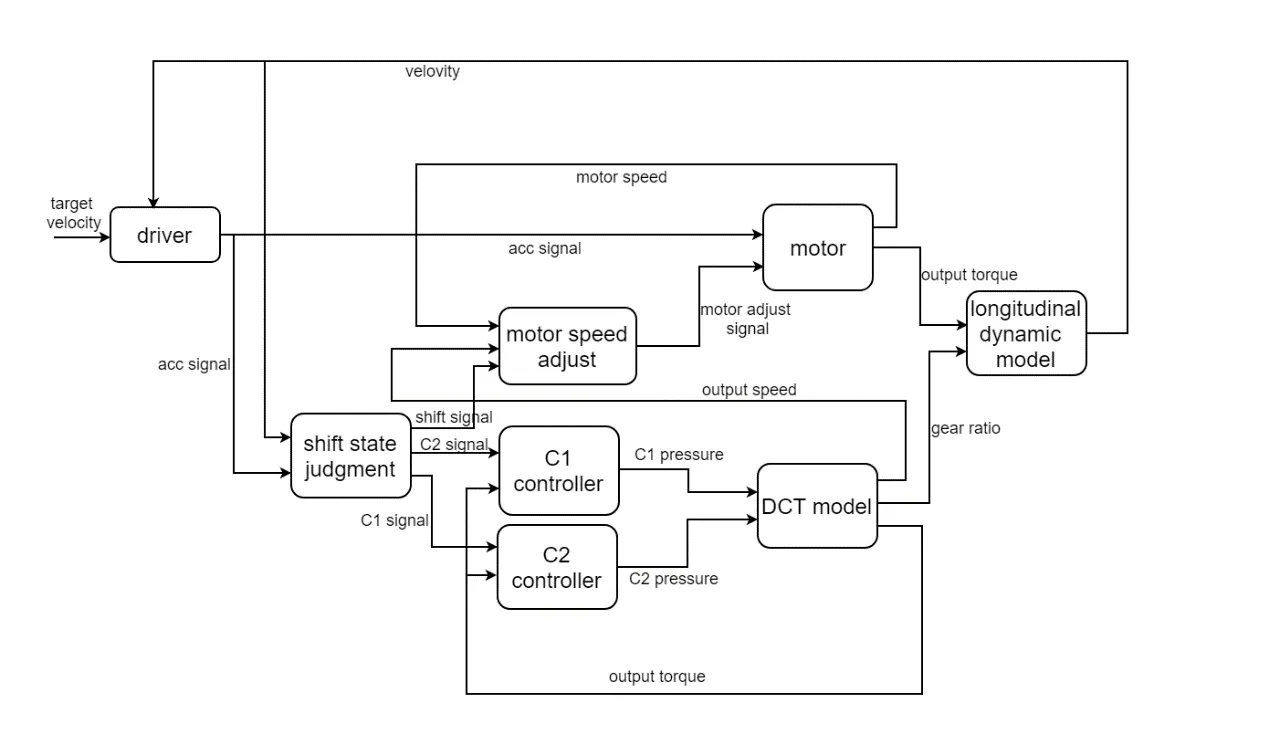
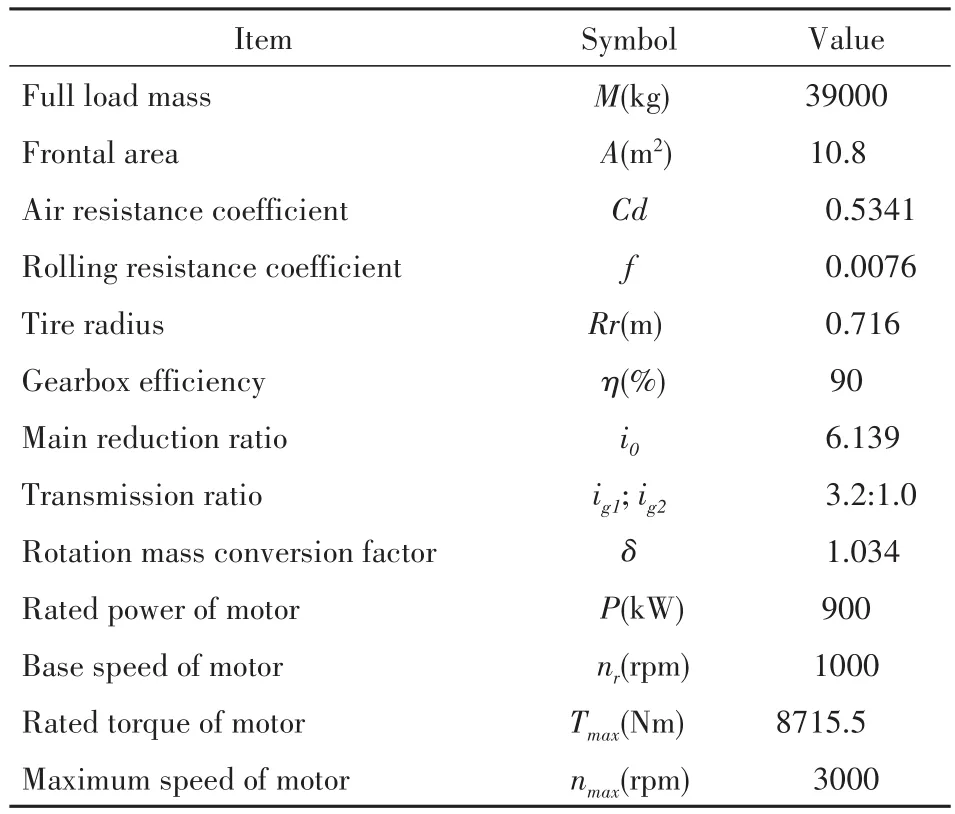
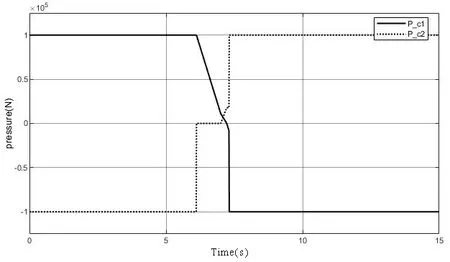
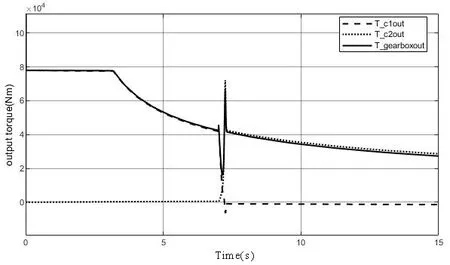
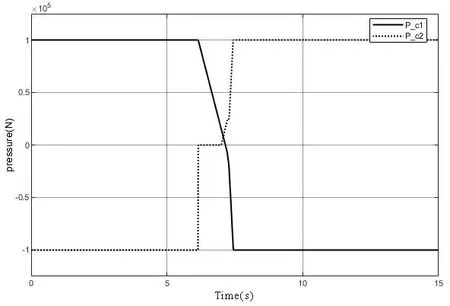
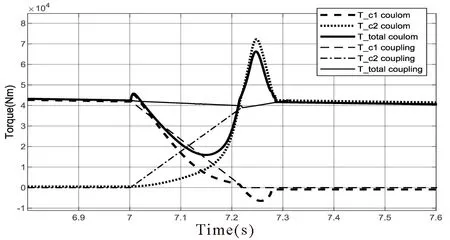
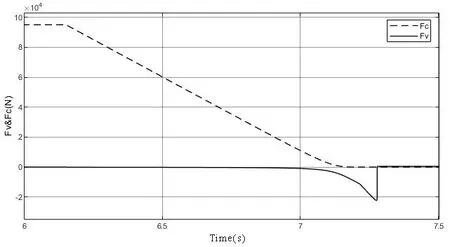
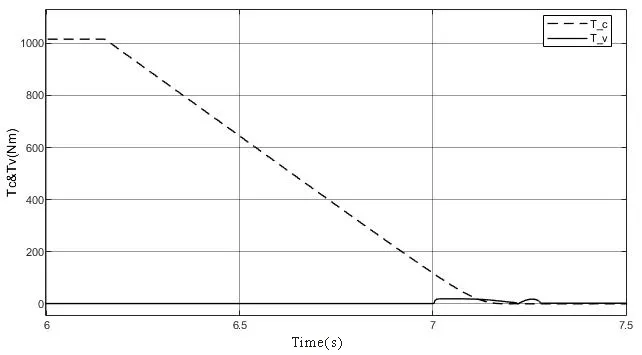
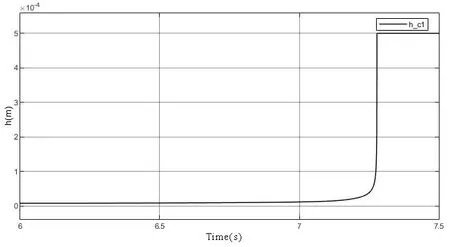
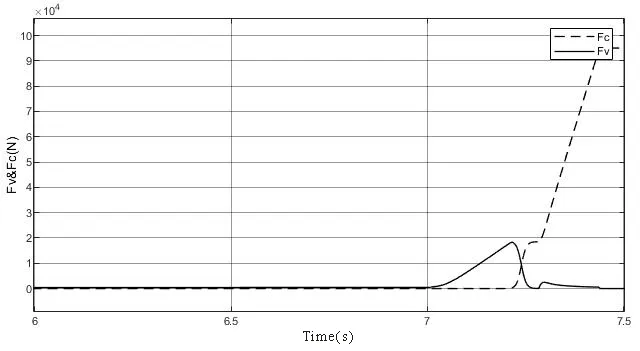
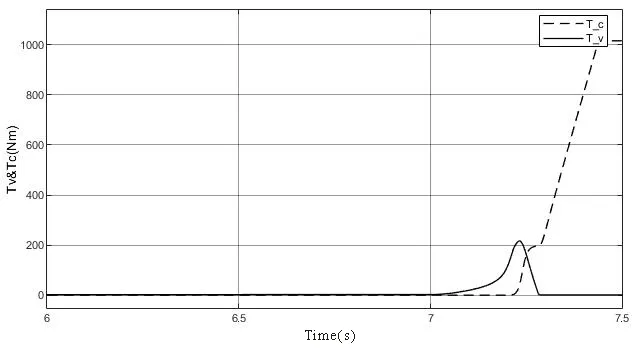
式(19)中,A0表示弹塑性接触系数,1 根据弹性力学模型,通过数值积分和曲线拟合[15],有效压力Pc与H的近似关系为: 参考文献[25],Kp选取常数4.4086×10-5,K´与E´分别为: 其中,E1、E2分别为摩擦副两个摩擦副的弹性模量,E´代表了当量弹性模量.在混合摩擦阶段,根据受力平衡,离合器的执行机构对离合器的压力应为液压承载力和接触承载力之和. 即压强Pc与Pv关于各自的面积积分.引入变量C=Ac/An表示粗糙摩擦面积占有效接触面积的比例.以Ared表示摩擦片实际受力区域占总面积的比例.能够得到混合摩擦液压力与接触压力分别为: 代入压强公式,积分得到Fv,Fc的值: 当已知离合器正压力Fn时,即可解得离合器摩擦片间的间隙变化率∂h/∂t,此时可求出油膜压力和摩擦接触力的数值.根据摩擦理论及1.2节所推导的液体剪切转矩计算公式,两者产生的传递力矩分别为: 考虑到摩擦系数随着相对转速增加而减小,摩擦系数与转速的关系式为: 其中,fc0为滑动摩擦系数,k为摩擦系数随转速差下降速度的参数,kf为静摩擦系数高于滑动摩擦系数的比值.参考文献[19]取值. 当离合器间隙进一步减小,摩擦片间隙无法形成油膜,传递转矩即为微凸体的摩擦转矩,接触面积比C=1.则式(30)改为: 整车功率传递路线为:从电机输出功率,传递至双离合减速箱,再由主减速机依次传递至主传动轴和轮边,驱动车辆行驶.在纵向动力学模型中,以上各部件依次考虑到:电机的动态特性,双离合减速机的离合器传递转矩,双离合减速机内部齿轮轴的转动惯量,主减速机的转动惯量,主传动轴的转动惯量,刚度和阻尼,轮边的转动惯量,轮胎与路面的附着系数,车辆的总行驶阻力. 根据车辆纵向动力学公式,车辆行驶阻力组成为: 其中,Ff为滚动阻力,Fw为空气阻力,Fi为坡度阻力,Fj为加速阻力.与车速、路面条件等关系如下: 其中,G为整车车重(N),Cd为风阻系数,A为迎风面积(m2),ua为车速(km/h),f为路面滚阻系数,δ为汽车旋转质量换算系数,商用车轮胎滚阻系数和旋转质量换算系数公式如下 其中,Iw为车轮转动惯量,If为主传动部分转动惯量,Ig为变速箱内转动惯量(根据档位决定),i0为主传动比,ig为对应档位速比,ηT,ηg为主减速机和变速箱传动效率. DCT换挡的本质为传递转矩从当前档位离合器逐渐转移至目标档位离合器的过程.离合器滑摩过程中,传递转矩可以表示为: 其中,ωrel1=ωc1-ωm,ωrel2=ωc2-ωm,Tc,Tv分别为章节1中计算的摩擦片传递转矩和油液传递转矩,当电机转速与离合器1转速同步,且传递转矩小于离合器最大传递转矩,则离合器维持啮合状态,传递转矩为电机转矩减去离合器2的滑摩转矩(离合器1,2不存在同时接合情况);当电机转速大于离合器1转速,则传递转矩为正;当电机转速小于离合器1转速,则传递转矩为负. 结合整车纵向动力学方程,式(42)为两自由度方程: 其中,ce表示电机转动副阻尼系数为等效到减速机输出轴的等效转动阻尼系数为等效到减速机输出轴的等效转动惯量. 其中,Ig1,Ig2表示变速箱一档与二档动力传递路径的转动惯量,cg1,cg2表示对应动力传递路径的摩擦阻尼,If表示减速箱转动惯量,cf表示减速箱转动副的摩擦阻尼.ηg,ηf表示变速箱到车轮及减速箱到车轮的传动效率. 上述动力学模型着重于车辆动力系统功率流的实时计算,通过湿式离合器的精细建模仿真换挡过程的响应,考虑了离合器的转动自由度和纵向进给自由度. 湿式双离合换挡整车系统模型的换挡控制框图如图1所示.具体如下: 图1 湿式双离合变速器整车系统模型示意图Fig.1 Wet-type DCT shifting vehicle system model (1)根据目标车速、路况信息得到驾驶员的加减速意图,转换为油门信号输入至电机及换挡控制模块; (2)电机接受油门信号后输出转矩,经过变速箱的传递驱动整车行驶,通过纵向动力学模型的计算得到车辆的加速度,经过积分得到车速信息; (3)根据油门信号及车速情况进行判断的换挡控制模块作出换挡响应,将换挡响应信号输出至电机调速模块和离合器油缸控制模块协调完成换挡动作; (4)DCT变速箱根据输入油压信号进行动力学计算,获取动态换挡过程. 本文采用Matlab/Simulink软件平台,搭建了双离合换挡整车系统模型及换挡控制策略进行仿真分析.模型关键参数如下: 表1 DCT摩擦模型关键参数Table 1 Key parameters of DCT friction models 当将湿式离合器模型视为经典库伦摩擦模型时,离合器传递转矩与压力的关系呈式(44)和式(45)所示: 表2 整车模型关键参数Table 2 Key parameters of vehicle models 上式中,传递转矩与压力关系基本为线性相关,以0.5油门开度的换挡工况为例,采用了用既定策略的开环控制方式,分析换挡的动态过程.换挡逻辑[24]为: (1)变速箱接收到换挡信号时,离合器应当进入准备阶段,即接合离合器逐渐松开至即将滑摩的状态,待接合离合器逐渐压接,排除空行程,如图中P1阶段所示; (2)此后接合离合器继续放松,换挡控制器控制待接合离合器增压,使总变速箱总输出转矩不变,如图中P2阶段所示; (3)待分离离合器完全松开,DCT换挡进入惯性相阶段,该阶段离合器接合压力不变,而电机进入调速阶段,调节电机转速至与待接合离合器转速一致如图中P3阶段所示 (4)完成调速后,离合器压紧,完成换挡. 将该控制策略应用于基于库伦摩擦的双离合换挡模型后,仿真结果如图3-图4所示,其中,图2是换挡过程中输出转矩变化的仿真值,图3为换挡过程中正常加压过程的离合器压力仿真值,图4为图2的局部放大图,用于体现换挡动态过程.在离合器C1、C2均处于滑移状态时,由于离合器传递转矩与接合压力成正比关系,换挡过程中离合器油压如图5所示:当C1油压递减时,传递转矩同步递减,同时离合器C2油压递增,传递转矩同步递增,双离合变速器总输出转矩基本维持不变,将两个离合器的传递转矩等效计算至双离合变速器输出端后,C1等效转矩减小速率与C2等效转矩提升速率一致,如图6所示,即总输出转矩基本维持不变,实现了无动力中断换档的目的. 图2 双离合变速器输出转矩(库伦模型)Fig.2 Output torque of DCT(coulomb model) 图3 双离合变速器控制油压(库伦模型)Fig.3 Pressure of DCT controller(coulomb model) 图4 双离合变速器传递转矩_局部放大(库伦模型)Fig.4 Transmitted torque of DCT_Partial enlargement view(coulomb model) 考虑到实际应用中,力矩传感器布置困难且成本较高,力矩反馈较难实现.开环控制在实际应用中占据了主导地位.然而对于干式离合器,传递转矩与压力关系基本为线性相关,而湿式离合器中,传递转矩的形成滞后明显. 以0.5油门开度的换挡工况为例,采用液固耦合模型搭建双离合变速器动力学模型,并用上文所述控制策略进行换挡控制,分析双离合变速器在换挡过程中的特性. 在换挡过程初期对离合器C1匀速降压,对离合器C2匀速升压,产生的传递转矩呈现明显的非线性变化,如图9所示,在换挡的前0.2s中离合器C2传递转矩变化极缓慢,而离合器C1传递转矩迅速降低,导致变速箱输出转矩存在明显波动,产生功率缺口.图5中显示,在0.5油门开度情况下DCT换挡过程中传递转矩缺口约为22000Nm.当图6中C2控制油压线性上升时图7传递转矩并未随之提升,此后当湿式离合器C2的摩擦片产生接触,进入混合摩擦阶段,传递转矩迅速提高,即前文所讨论的湿式离合器接合过程传递转矩滞后问题,重点关注换挡发生的7s~7.5s时间段内,两种模型对应仿真结果如图8所示. 图5 双离合变速器传递转矩(耦合模型)Fig.5 Transmitted torque of DCT(coupling model) 图6 双离合变速器控制油压(耦合模型)Fig.6 Pressure of DCT(coupling model) 图7 双离合变速器传递转矩_局部放大(耦合模型)Fig.7 Transmitted torque of DCT_Partial enlargement view(coupling model) 图8 双离合变速器传递转矩_局部放大(综合)Fig.8 Transmitted torque of DCT_Partial enlargement view(complex) 当未考虑湿式离合器的动态接合过程时,仿真得到该换挡过程有明显动力中断,换挡冲击度较大.下文中通过分析离合器内部力矩和压力在微凸体和润滑油液之间的分配研究湿式双离合变速器的换挡响应滞后问题. 在接合过程中,C1中润滑液与摩擦片分别承担的传递转矩与压力如图9图10所示.C1离合器释放过程中,润滑油液压及粘性转矩小,摩擦片摩擦转矩随正压力变化,响应基本无延迟.离合器间隙在7.2s之前出于粗糙接触阶段,在7.2s之后快速释放,传递转矩接近于0Nm;C2离合器中润滑油与摩擦片分别承担的传递转矩与压力如图12图13所示.在7.25s之前,离合器处于挤压油液阶段,正压力和传递转矩均由润滑油部分承担,传递转矩较小.此后进入粗糙接触阶段,摩擦片正压力和摩擦转矩迅速上升.故整体传递转矩存在滞后. 图9 离合器C1粗糙接触正压力Fc/油膜正压力Fv变化Fig.9 Contact pressure(Fc)/oil film pressure(Fv)of clutch 1 图10 离合器C1粗糙接触转矩Tc/油膜粘性转矩Tv变化Fig.10 Contact friction torque(Tc)/viscosity torque(Tv)of clutch1 图11 离合器C1间隙h变化Fig.11 Clearance(h)of clutch1 图12 离合器C2粗糙接触正压力Fc/油膜正压力Fv变化Fig.12 Contact pressure(Fc)/oil film pressure(Fv)of clutch 2 图13 离合器C2粗糙接触转矩Tc/油膜粘性转矩Tv变化Fig.13 Contact friction torque(Tc)/viscosity torque(Tv)of clutch2 为研究湿式离合器传递转矩的变化,本文引入了Patir-Cheng平均流量模型和G-W微凸体接触模型,建立了湿式离合器接触过程的固液耦合模型.发现在接合过程中,挤压油液阶段产生的传递转矩较小,受到接合压力和接合时间两个参数的影响,难以由接合压力单个参数进行控制,而在混合摩擦阶段和粗糙接触阶段,离合器的传递转矩受时间随接合压力的变化响应较迅速,易于通过油压直接控制.根据仿真结果得到了挤压油液阶段时间、最大粘性转矩、摩擦转矩等与接合压力的关系. 图14 离合器C1间隙h变化Fig.14 Clearance(h)of clutch2 本文根据车辆纵向动力学建立了整车仿真模型,包含了电机特性,变速箱档位转换,车辆行驶方程计算等模块,搭建了可靠的整车系统研究平台.在湿式双离合变速器整车系统模型中,研究了换挡过程的动力学特性,对比采用经典库伦摩擦方式搭建的双离合变速器模型,以基于规则的双离合变速器换挡策略进行换挡过程仿真.仿真结果显示,采用Patir-Cheng平均流量模型和G-W微凸体接触模型进行建模的湿式双离合变速器在转矩相过程中存在明显的转矩响应滞后,而该特征无法在库伦摩擦模型中体现. 进一步对湿式离合器油膜和摩擦片分别承担的正压力和传递转矩进行分析,该响应滞后现象主要由挤压油液阶段和混合摩擦阶段离合器转矩特性的差异造成.在挤压油液阶段,湿式离合器摩擦片传递转矩随接合压力提升较缓慢,而在混合摩擦阶段提升较快.湿式双离合变速器在换挡过程中,接合离合器在释放过程中分别经历粗糙接触阶段,混合摩擦阶段和挤压油液阶段,而对于分离离合器,在接合过程中则是先经历挤压油液阶段,后经历混合摩擦和粗糙接触阶段,其转矩-压力/接合时间的函数差异较大,难以形成转矩互补.库伦摩擦模型中以同一传递函数进行描述的方法具有较大误差. 研究表明,引入微凸体接触和平均流量方程的湿式双离合变速器模型能够更准确地反应换挡动力中断和响应滞后现象.在本文结论的基础上,基于该仿真模型能更准确地研究换挡的动力中断现象,为制定高换挡平顺性的控制策略提供支持.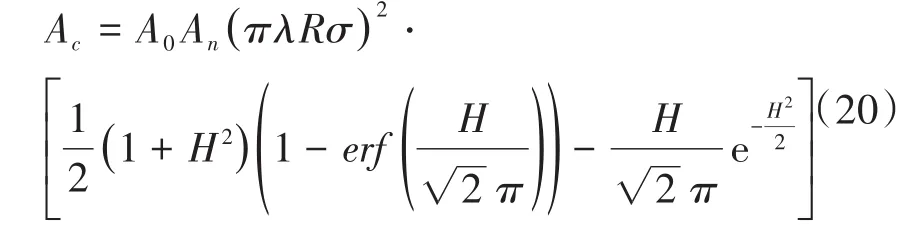
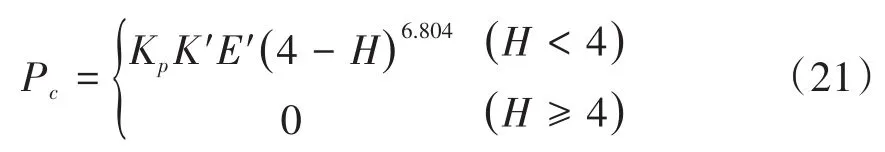
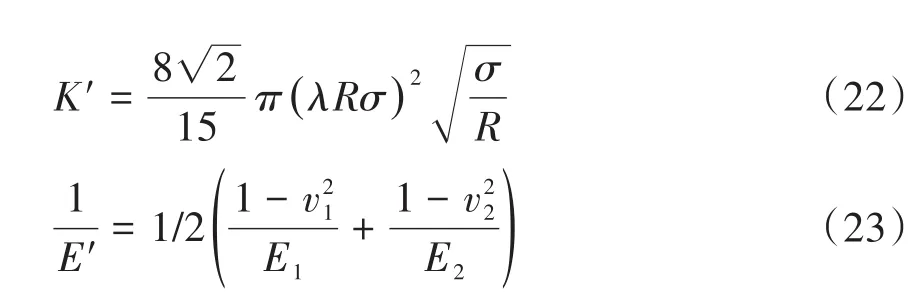

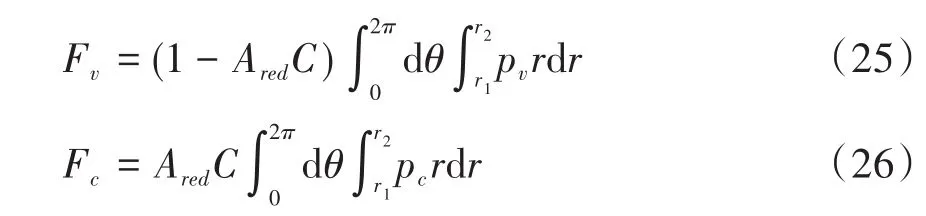

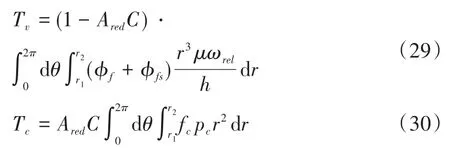
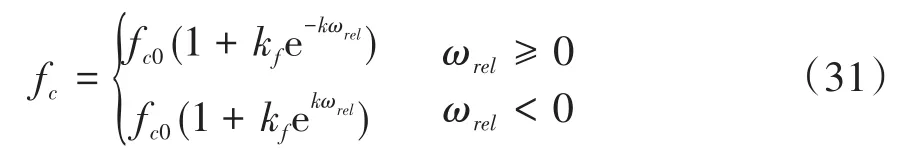
1.4 粗糙接触阶段
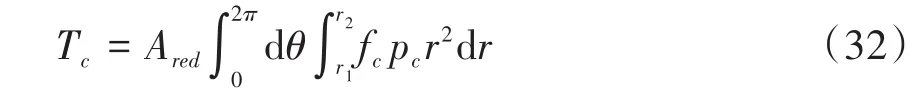
2 整车纵向动力学建模
2.1 车辆行驶阻力模型
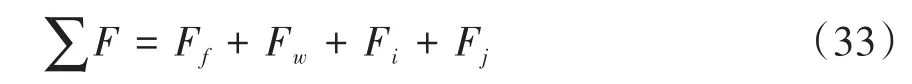


2.2 DCT换挡动力学方程

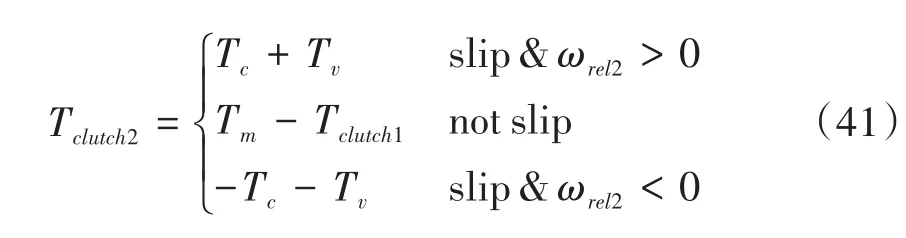

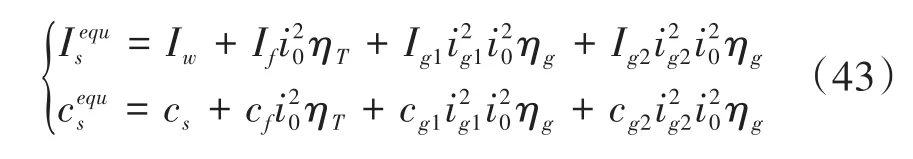
3 仿真计算
3.1 库伦摩擦模型仿真



3.2 液固耦合模型仿真

4 小结