地月L2点中继星捕获域研究*

梁伟光 马传令 刘勇 刘磊

（1.北京航天飞行控制中心，北京100094）（2.航天飞行动力学技术重点实验室，北京100094）

引言

月球自转周期与绕地球公转周期相同的特性，使得在月球背面进行着陆探测时，探测器无法直接与地面测控站通信.地月L2平动点（下文简称“L2点”）位于地球至月球连线的延长线上，即月球背面的“正上空”，且与地球、月球的位置相对固定.航天器在地月系L2点附近可以环绕L2点飞行，对月球背面持续可见.因而在地月系L2点布设中继卫星，建立“地面-中继星-月球背面”的中继通信链路，能够有效支持月球背面着陆探测.

在地月L2点布设中继星的想法最初由美国航空航天局（NASA）于20世纪60年代在论证阿波罗18任务时首次提出，并基于此提出了共线平动点单圈周期轨道——halo轨道的概念［1］，后来因阿波罗计划的整体终止未付诸实施.我国的嫦娥四号任务于2018年首次实现了在地月L2点布设中继星“鹊桥”号，选用固定振幅的南簇halo轨道作为使命轨道，为嫦娥四号探测器着陆月球背面时提供中继通信支持.

航天器绕飞地月L2点的任务此前还实施过两次，分别为美国的ARTEMIS任务［2］和我国的探月工程三期再入返回飞行试验器服务舱拓展试验任务.两次任务均作为拓展试验，实现了沿Lissajous轨道绕飞地月系L2平动点多圈.

相较Lissajous轨道，halo轨道由于不存在月掩［3，4］，更适合作为中继卫星轨道.然而halo轨道在空间构型、捕获精度、位置保持等方面均较Lissajous轨道具有更高的实施难度.在放宽月掩约束的基础上，地月L2点中继星也可考虑以限制相对较弱的Lissajous轨道作为捕获轨道，实现月掩外较为高效的月球背面中继通信支持.由此，可衍生出针对地月L2点中继星绕飞地月L2点的捕获域问题.目前，尚未见关于地月L2点中继星捕获域方面的公开文献.

本文针对地月L2点中继星捕获域展开系列分析，所得结论可以用于为相似任务的轨道设计、约束影响、区域选择等内容提供技术支持和量化参考.

1 动力学理论

地月L2点中继星捕获域是指中继星能够提供地月中继通信服务的前提下，在地月L2点附近实现绕飞的动力学捕获范围.研究地月L2点中继星捕获域的动力学模型基础是三体问题平动点轨道和零速度面.

1.1 三体问题

开展地月L2点中继星捕获域研究的动力学基础是三体问题.对于三个天体，当质量、初始位置和初始速度均已知，研究它们在万有引力作用下的运动规律问题，称为三体问题.在三体问题中，当有一个天体的质量与其它两个天体的质量相比，小到可以忽略，称为限制性三体问题.在限制性三体问题中，假设两个大质量天体绕公共质心作匀速圆周运动，称为圆型限制性三体问题（circular restricted three-body problem，CRTBP）.在地月系三体问题中，航天器作为人造天体，其质量远小于地球和月球质量，因此地月系三体问题可以简化为限制性三体问题或圆型限制性三体问题.

会合坐标系（又称质心旋转坐标系）［5，6］是研究三体问题时普遍采用的坐标系.会合坐标系O-xyz的定义为：坐标系随两个主天体一起绕共同质心O旋转，xy平面为两个主天体相对运动的平面，x轴方向由大天体指小天体，y轴方向为小天体绕质心旋转的切线方向.具体至地月系三体问题，O为地月系质心，xy平面为白道面，x轴方向由地球指向月球，y轴方向为月球在惯性系中运动的切线方向.

根据牛顿万有引力定律，航天器在两个主天体P1和P2的引力作用下的运动方程为：

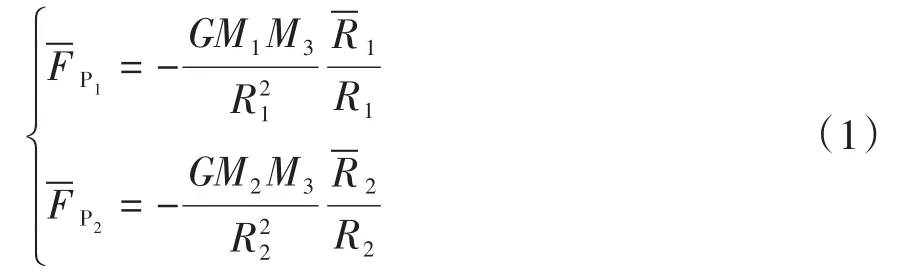
其中，G为万有引力常数.为了分析问题和计算上的方便，对式（1）中各物理量进行无量纲化和量级归一化处理，可以得到会合坐标系中的圆型限制性三体问题动力学模型如下：

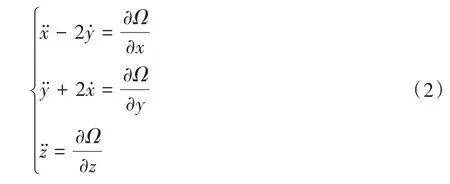
其中，Ω为等效势能函数，

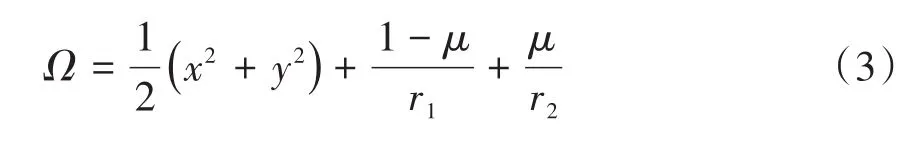
μ为小天体的质量占比，

1.2 平动点

三体问题基本方程（2）存在五个特解，对应的空间中的位置称为平动点，又称拉格朗日点，用L1～L5表示.其中，L2平动点位于大天体至小天体的质心连线延长线上，是三体问题中的不稳定平衡点，航天器在L2平动点附近飞行时经过小扰动，即会呈近似指数型远离L2平动点.

地月系L2点距离月球约6.4万千米，Ω在地月系中的分布如图1所示.该等势面有三个鞍点和两个极大值点，分别对应了平动点L1、L2、L3和L4、L5.

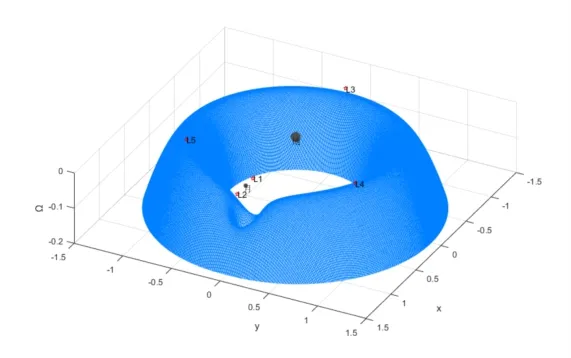
图1 地月系等效势能曲面Fig.1 Equipotential surface of Earth-Moon system

1.3 零速度面

当等效势能Ω取固定值时，在空间中对应构成的曲面是运动允许区域（V2≥0）和禁止区域（V2＜0）的分界面，在该面上V2=0，即V=0，称为零速度曲面，也称为希尔曲面.零速度曲面可以直观反映第三体的可能运动区域.

图2为地月系平动点附近的零速度曲面.图中绘制了不同Ω时的零速度曲面，各色曲面对应的等效势能Ω中，绿色最小，红色次之，蓝色最大.当z=0时，零速度曲面退化为xy平面内的环状区域，对应图1中相同Ω的切面，反映了二维运动区域边界，如图3所示，其中各图对应的Ω依次增加.可能运动区域为包含地球和月球的区域.

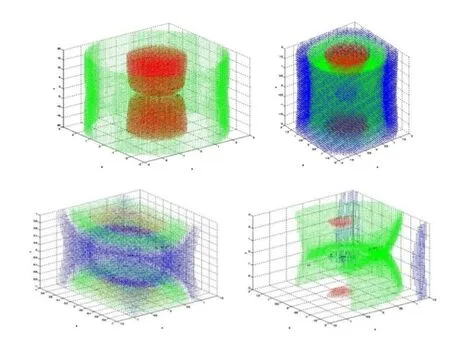
图2 地月系平动点附近零速度曲面Fig.2 Zero velocity surfaces near Earth-Moon libration points

由图3可以看出：（1）能量较小时，第三体仅能在地球或月球附近飞行；（2）能量增加时，地球附近和月球附近的运动允许区域在L1点处联通，第三体经由L1点可在地月附近往返，但不能飞出地月系；（3）能量继续增加时，运动允许区域在L2点处开口，第三体经由L2点可飞离地月系；（4）随着能量增加，运动禁止区域逐渐收缩至三角平动点附近，最终消失，从而实现三体模型下全空间可达.

图3 地月系平动点附近等势切面Fig.3 Equivalent potential energy profiles near earth-moon libration points

1.4 L2平动点轨道

L2平动点位于大天体至小天体的质心连线延长线上，属于共线平动点，是三体问题中的鞍型不稳定平衡点，航天器在L2平动点附近飞行时经过小扰动，即会呈近似指数型远离L2平动点.在L2平动点附近存在多种类型的周期和拟周期轨道，其中以下三类轨道在研究和应用方面较为广泛［7］：

（1）Halo轨道.当会合坐标系下轨道平面（xy平面）振动频率与垂直（z向）振动频率相等时，第三体环绕平动点的轨道呈单圈闭合形式，称为halo轨道，又称晕轨道.Halo轨道是周期轨道.由于实际情况很难满足“平面振动频率与垂直振动频率相等”，因此halo轨道通常仅作为理论轨道加以分析.

（2）Lissajous轨道.当会合坐标系下轨道平面振动频率与垂直振动频率不相等时，第三体环绕平动点的轨道在会合坐标系下呈Lissajous曲线的形式，称为Lissajous轨道.平动点环绕轨道中Lissajous轨道占多数.

（3）拟halo轨道.拟halo轨道为一类特殊形式的Lissajous轨道，这类轨道在halo轨道附近，其偏离halo轨道面的振动幅值较小.拟halo轨道是一种拟周期轨道，即没有严格的周期性，但在特定的偏差允许范围内，表现出近似的周期性.现实三体系统由于受到多种摄动影响，不存在严格周期性的理想halo轨道，但是halo轨道所具有的单圈周期性、轨道近似共面、解析近似形式简单、动力学特性明显等良好特征，使得寻找与halo轨道近似的拟halo轨道往往成为平动点任务的现实需求.

2 地月L2点中继星捕获域影响分析

地月L2点中继星的使命轨道首选环绕地月L2点的拟halo轨道.如受其他条件制约而临时重构或应急捕获时，可以考虑捕获为Lissajous轨道的替代方式，以继续实现中继通信支持.本文针对以Lissajous轨道作为中继任务轨道的情况，结合工程需求与约束，开展系列分析.

2.1 月掩影响

掩星是指一个天体在另一个天体和观测者之间通过而产生的遮蔽现象.由月球遮蔽引起掩星现象又称为月掩.在地月L2点附近即存在月掩现象，如图4所示［4］.

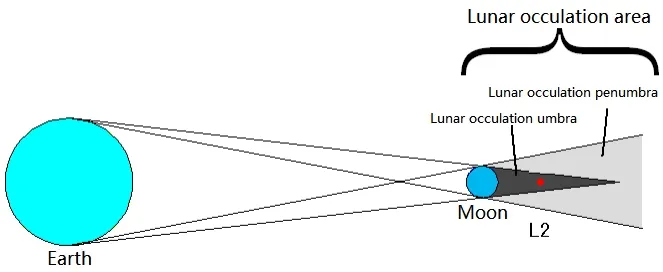
图4 月掩示意图Fig.4 Lunar occultation schematic diagram

月掩带位于地月L2点垂直地月连线切面外轮廓为圆形，半径为3107.9km.考虑到月球轨道偏心率影响，月掩带半径会有±11km的变化.考虑到地面站跟踪仰角大于0°的约束，从而导致测控弧段相较仰角0°约束时的情况有所缩短，从而使得通信范围的月掩本影半径增加，月掩半影外半径减小，月掩带范围不会扩大.基于上述考虑，并参考美国阿波罗项目中继卫星设计论证方案，将月掩半影外轮廓作为月掩边界的方法，可以保守地选取月掩带半径为3500km.当中继星运行在Lissajous轨道时，存在进入月掩带的可能，从而无法进行星地通信.

由于应急捕获Lissajous轨道的入口为发散状态，Lissajous轨道构型和中继星相位相应的难以定量确定，在此采取初始位置、初始方向、轨道振幅分别遍历的方法，对月掩影响进行多角度分析.选取遍历初始位置的最长规避持续时间，作为衡量其所对应轨道的指标，进而对不同轨道的振幅Ay和Az进行遍历.遍历后的规避持续时长分布如图5所示.由图5可得：无月掩持续时长与xy平面内振幅和z向振幅均相关.

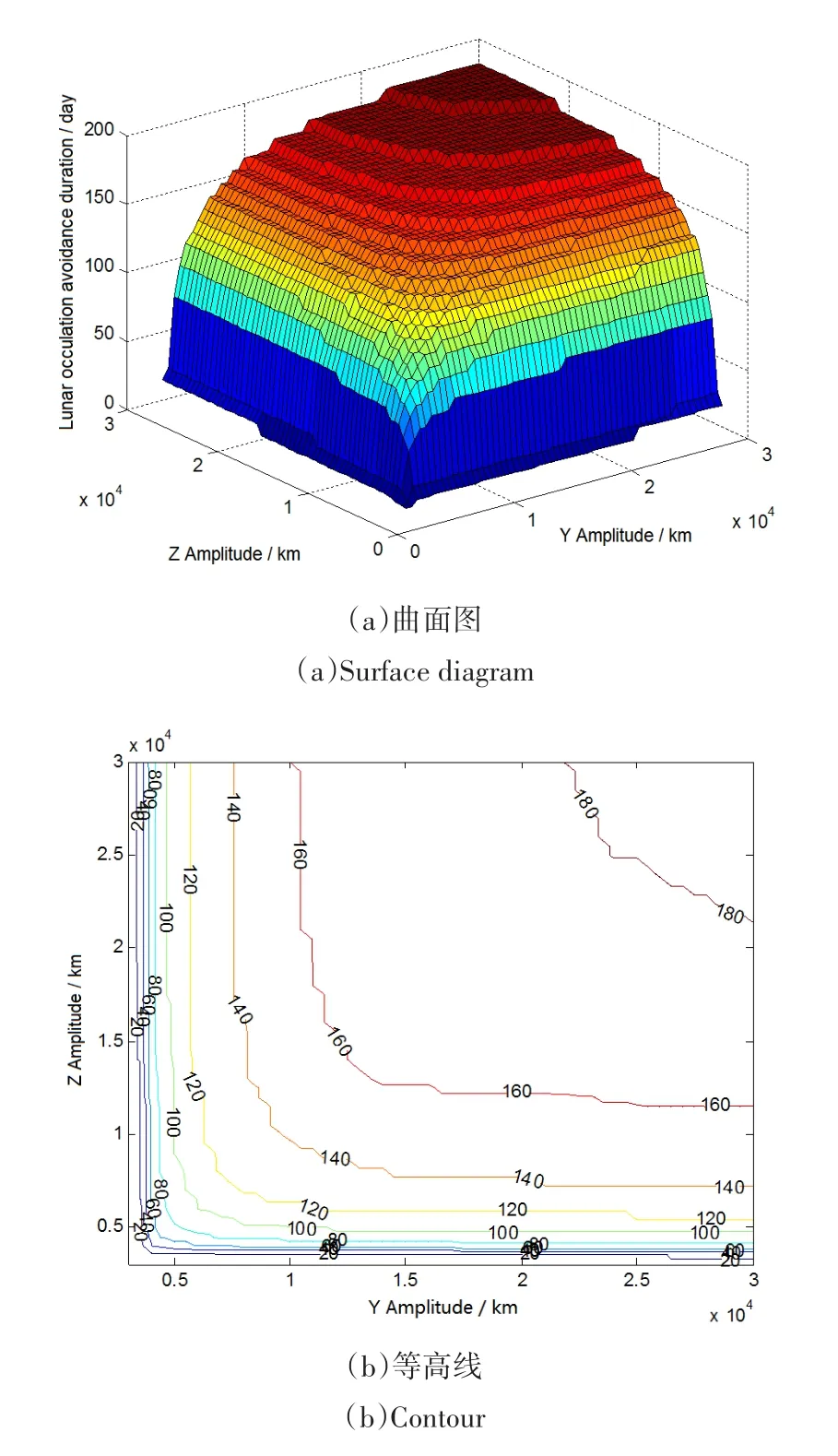
图5 遍历振幅的规避月掩持续时长Fig.5 Avoidance duration of lunar occultation with amplitude traversal

最长持续无月掩时长与最大振幅的关系如表1所示.

表1 Lissajous轨道最大振幅与最长持续无月掩时长关系Table 1 Relationship of Lissajous orbits maximum amplitude and the longest duration without lunar occultation

通过对最长规避时长对应的Lissajous轨道进行仿真，归纳得出以下规律：

1）卫星进入月掩的最长时长约为14小时，进入月掩时长约占总飞行时长的0.5%；

2）卫星频繁进入月掩期间的总时长约为20～30天，两次进入月掩的时间间隔约为7天.频繁进入月掩期间，进入月掩时长约占总时长的10%以下.

2.2 中继通信影响

由于振幅相同的halo轨道仅有两条（南簇、北簇各一条），而振幅相同的Lissajous轨道理论上有无数条.即针对相同能量的halo轨道，存在多条Lissajous轨道可供选择.在此，从三体系统等效势能的角度，把能量相同的Lissajous轨道的外包络面，即零速度面，作为中继通信的分析对象.当卫星沿Lissajous轨道长期飞行时，中继通信的约束边缘即分布于零速度面之上.

由于全部零速度面会将天体、平动点和轨道完全包住，难以直观观察，且零速度面相对xy平面对称，因此绘制半部分零速度，如图6所示.

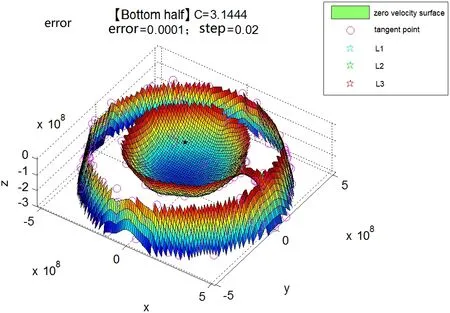
图6 下半部分零速度面Fig.6 Bottom half of zero velocity surface

Lissajous轨道的外包络即分布在零速度面在L2点附近的狭窄开口处.由于嫦娥四号的主备着陆区均在月球背面中点（经度180°，纬度0°）的西南，且零速度面也相对xz平面对称，因此截取零速度面在L2点附近的东北局部（即+y+z部分），即可作为偏离着陆点最远象限部分进行分析.零速度面的东北局部如图7所示.

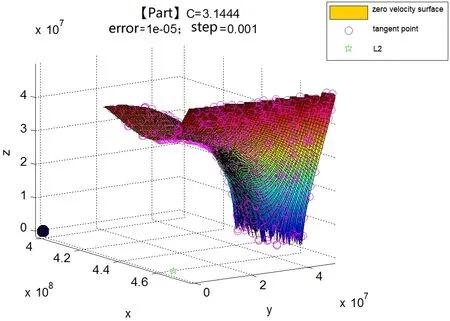
图7 L2点附近零速度面的东北局部Fig.7 Northeast part of zero velocity surface near L2 libration point

更进一步，Lissajous呈纺锤状构型，其外包络与零速度面东北局部的相交部分为一段弧线，将此弧线提取（图8），即可开展中继通信约束角分析（图9）.

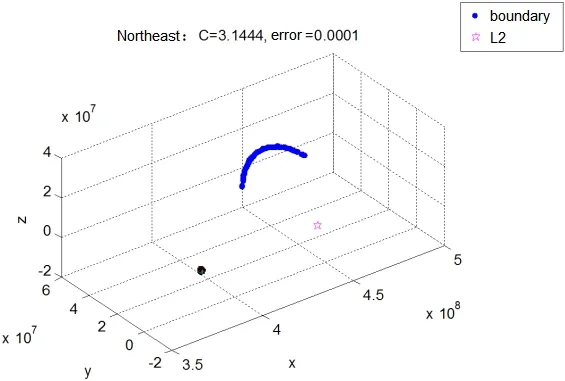
图8 Lissajous轨道与东北局部零速度面的交线Fig.8 Intersecting line of Lissajous orbit and northeast part of zero velocity surface

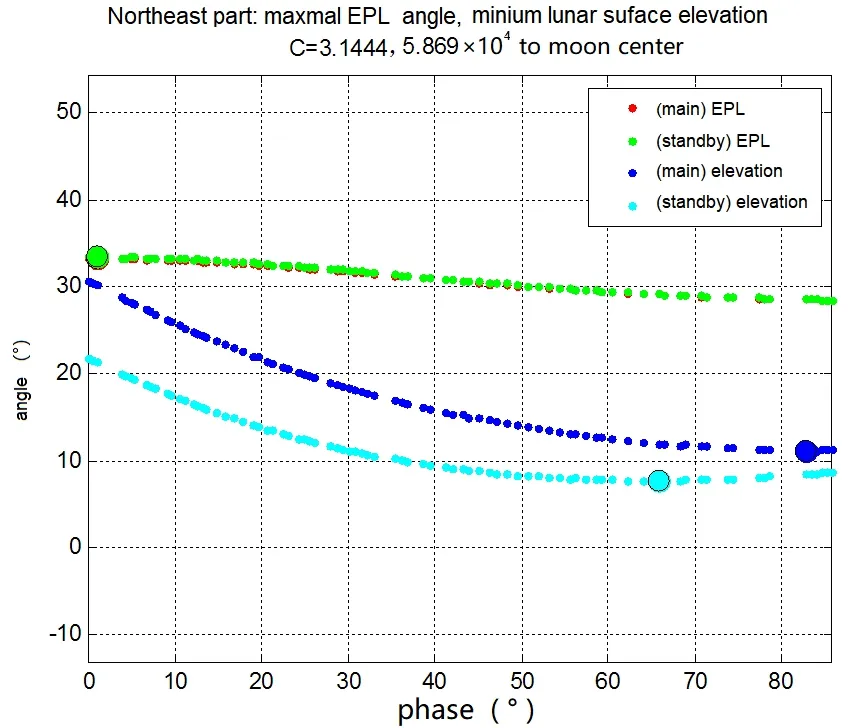
图9 交线上的中继约束角分析Fig.9 Analysis of relay constraint angle on intersecting line

在完成近月制动控制目标的基础上，可以分析形成不同Lissajous轨道时对测控和中继通信条件的影响，其中，势能等效ΔV在圆型限制性三体模型下依据等效势能C计算得出，即：

由此算得的ΔV是理论情况下形成Lissajous轨道的最小速度增量.工程实际中，受模型精度、选优方式、测控约束等条件影响，可能会有所偏差.

2.3 轨道维持影响

由于halo轨道有空间回归构型，在轨道维持方面，构型、演化、摄动等因素均对轨道维持的精度和推进剂消耗产生一定影响.相对而言，Lissajous轨道的空间构型约束较低，能够绕飞平动点即可，即使偏离标称轨道，仍为Lissajous轨道，且对任务无明显影响.因此，Lissajous轨道在长期轨道维持方面的寻优空间更大，相较halo轨道可以做到更省推进剂.然而，由于是在优化控制的技术上产生出的差别，Lissajous轨道节省推进剂的优势并不十分明显.

3 仿真算例

结合上述捕获域影响分析方法，基于嫦娥四号任务中继星飞行过程，选取了两种情况进行地月L2点捕获仿真计算：（1）近月制动后尽快实施地月L2点捕获；（2）将进入halo使命轨道捕获改为更节省能量的轨道捕获.两次捕获后的轨道辅以必要的轨道维持，形成长期环绕地月L2点的绕飞轨道，相应的轨道、零速度曲面即等效势能C值如图10所示.

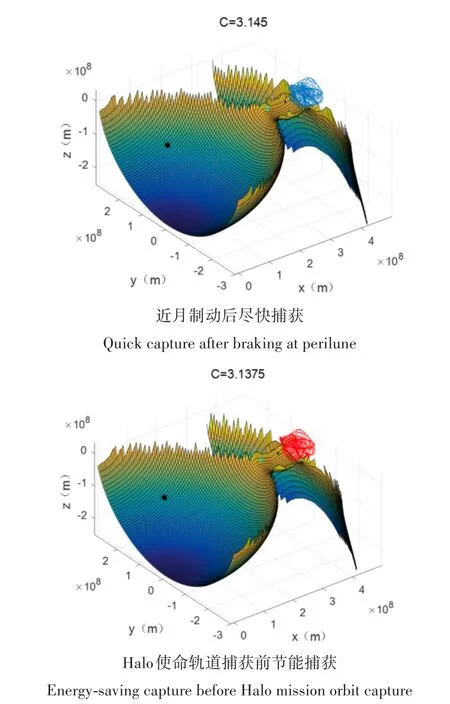
图10 地月L2点捕获轨道及对应的局部零速度曲面Fig.10 Earth-Moon L2 libration point capture orbit and corresponding partial zero velocity surface

由图10可以看出：（1）两种捕获方式均实现了Lissajous轨道绕飞；（2）两种捕获轨道空间构型相似；（3）由C值反映出两种捕获能量略有差别，其中近月制动后尽快捕获更省能量；（4）第3章所述的影响分析均适用于这两种捕获方式.

4 结语

本文针对地月L2点中继星的捕获域问题，从月掩、中继通信、轨道维持等多个影响方面，对中继星在地月L2点捕获的效果进行了理论分析、方法设计和仿真验证.研究结果表明：

（1）中继星如果沿地月L2点Lissajous轨道飞行，可以在大部分时间支持中继通信.进入月掩的占比较小，至多持续半天，且可以预报.

（2）近月制动后加速越大，形成Lissajous轨道振幅越大，由最大EPM角和月面最低仰角所反映出的Lissajous轨道边界处测控和中继通信效果越差.

（3）小振幅的Lissajous轨道，边界处测控和中继通信效果较好，但是月掩占比较高.

（4）Lissajous轨道可以满足基本的中继通信需求，因捕获域较广，存在节省能量的优化空间.

（5）Lissajous轨道在测控和中继通信方面的约束，需结合边界大夹角通信和包络中心月掩无通信的情况，加以综合考虑.

本文针对地月L2点中继星捕获域的分析方法和结论，也可以应用至载人登月、行星探测、平动点导航等其他基于三体动力学开展轨道设计的领域，有助于为后续相关工程任务轨道设计提供技术积累与参考.