基于刚体卫星绳系编队系统的动力学建模及姿态控制*
赵俊淇 陈卫东† 余本嵩,2
(1.南京航空航天大学机械结构力学及控制国家重点实验室,南京210016)
(2.大连理工大学工业装备结构分析国家重点实验室,大连116024)
引言
空间绳系卫星系统(Tethered Satellite System),简称TSS,是通过系绳将两个或者多个卫星连接起来,最初的设想是空间绳系卫星系统由母星和子星以及系绳构成,系绳两端分别连接母星和子星,母星利用卷扬机构对子星进行释放或回收.根据系绳导电与否,绳系卫星系统可分为电动力系统和非电动力系统两大类.多体绳系卫星编队系统是由两体绳系卫星系统演化而来,通常由多个卫星或航天器在空间范围内相对静止地组成某种特定的构形.绳系卫星系统具有低成本,高灵活性,高性能等优势,因此受到国内外学者的广泛关注[1-7].
三体绳系卫星系统,由三颗卫星通过系绳首尾相连,通过自旋张紧系绳形成稳定的空间姿态,可节省用于调节系统姿态以及卫星相对位置的燃料,因此具有很大的研究意义.Kumar等将卫星视为质点,忽略系绳质量,通过拉格朗日法得到椭圆轨道中不包括卫星质量和系绳长度的系统运动控制方程的一般形式,通过数值模拟验证了三体绳系卫星系统的可行性[8].Kim等对三角形绳系卫星编队进行了研究,提出通过控制系绳长度降低整体所需的推理水平从而实现节省燃料的目的[9].Nakaya等将航天器视为刚体,提出基于虚拟结构方法,研究三体绳系卫星编队展开过程中通过角动量以及系绳张力实现控制方法实现系统展开[10].Topal等将卫星视为质点,对等边三角形绳系卫星系统进行动力学建模,得到了低地球圆轨道上运行的旋转三角形绳系卫星系统的姿态稳定方程[11].Williams将卫星视为质点进行动力学建模,基于系绳张力控制,对三体绳系卫星系统自旋展开的问题进行了研究[12].陈志明针对三星编队问题提出一种通过系绳连接的方法基于自选刚体卫星的平衡分析,建立了两种平衡构型的绳系卫星编队方法,并分析了稳定性[13].Yu等忽略卫星刚体姿态,研究了空间三体绳系卫星编队系统的自旋稳定性并进行了实验验证[14].Cai等将航天器视为质点,研究了释放和回收阶段平动点附近的旋转三角形绳系卫星系统的动态稳定性,并且讨论了初始系统旋转速率与耦合轨道振幅对释放回收阶段的影响,并得到绳长对系统质心运动影响不大作为对三角形绳系卫星研究的基础[15,16].黄静等人对于考虑刚体的欠驱动绳系卫星系统进行跟踪控制[17].Bonzani等考虑刚体卫星对经典两体绳系卫星建模并分析了大气阻力对系统稳定性的影响[18].Huang等人对于辐形绳系卫星进行考虑刚体卫星姿态的展开控制研究[19].
本文考虑卫星的刚体姿态的影响,对三体环形绳系卫星编队系统的动力学模型进行研究.采用四元数法,避免方程奇异值,采用Newton-Euler法建立动力学模型,得到包含四元数的可求解的卫星运动方程.基于此动力学模型,分析三体绳系卫星编队系统的动力学响应.对于扭矩造成的卫星姿态不稳定,通过施加控制力进行主动控制.
1 系统动力学建模
三颗质量相同的卫星S1、S2、S3通过系绳两两相连组成三体绳系卫星编队系统.卫星质量相等为m,将卫星视为半径为rc的球体,相对各自质心的转动惯量为J.由刚度为EA,原长为L的系绳连接.忽略J2摄动以及大气阻力,引入三组坐标参考系,设地球为均质圆球体,建立固结于地球质心O,X轴指向升交点,Z轴垂直于轨道平面的惯性坐标系O-XYZ;同时以系统质心o为原点,x轴为系统质心运动的反方向,y轴由地球质心指向系统质心建立轨道坐标系o-xyz;另外,对于卫星Si,以卫星质心oi为原点,yi轴由系统质心指向卫星质心,zi轴平行于惯性坐标系Z轴建立本体坐标系oi-xiyizi.本文在惯性坐标系O-XYZ下建模.
系统为正三角形形状,对一颗卫星动力学建模,类推到另外两卫星.刚体卫星Si共有6个自由度,即质心运动三个移动自由度和绕质心转动三个转动自由度.在惯性系下,通过笛卡尔坐标系Xi、Yi、Zi表示刚体的质心位置,对于刚体姿态,采用四元数λi0、λi1、λi2、λi3代替欧拉角,未知变量增加为7个.根据Newton第二定律,列出惯性系下的质心运动方程:

其中,i,j,k=1,2,3,mi为卫星Si的质量,r̈i=(Ẍi,Ÿi,Z̈i)表示惯性系下卫星Si的位置矢量,Fi为卫星Si受到的万有引力,Tij、Tik为卫星Si受到的系绳拉力.惯性系下卫星Si刚体动力学方程为:

其中,i,j,k=1,2,3,ωi为刚体的角速度,Ji为卫星Si的惯量张量,Mi为卫星Si的万有引力主矩,Nij及Nik为系绳拉力产生的力矩.
考虑本体坐标系下卫星Si的万有引力,系统质心所在轨道高度为H,地球平均半径为RE,为方便辨别,将本体坐标系下变量右下角加(i),α1,β1,γ1、α2,β2,γ2、α3,β3,γ3分别是本体坐标系oi-xiyizi中xi轴、yi轴、zi轴与惯性系X,Y,Z轴的方向余弦.设地球质心O相对于刚体任意位置的微元质量dm的径矢为ri´(i),有:

其中r为地球质心相对于刚体质心的距离大小,作用于微元质量dm的万有引力主矢dF和对oi的主矩dM为:
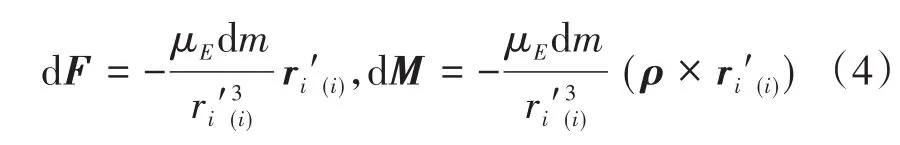
其中,ρi(i)=(xi(i),yi(i),zi(i)),dm为相对于刚体质心oi的径矢,在刚体域内积分,可得卫星Si在本体坐标系下的万有引力主矢Fi和主矩Mi,可以通过转换矩阵变换到惯性系下的万有引力主矢和主矩.
考虑刚体受到的系绳拉力,认为系绳质量很小,忽略不计.卫星上系绳连接处位置如图1所示.假设系绳连接处位置位于轨道坐标系的x,y平面,系绳连接处延长相交于卫星表面,由此可以确定系绳连接处位置,在本体坐标系下oi-xiyizi,卫星Si的系绳连接处位置ai、bi,相应另外两颗卫星的位置在各自的本体坐标系下表示为aj、bj及ak、bk,转换到惯性系下后可以进行计算,得到系绳实际实时长度.记另两颗卫星分别为Sj、Sk,卫星Si相连的两根系绳拉力分别是:
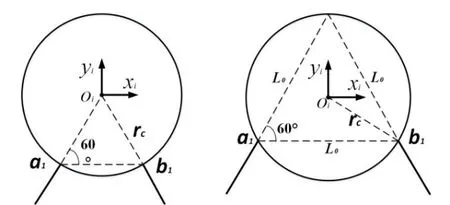
图1 轨道坐标系下x,y平面系绳位置示意图Fig.1 Schematic diagram of the position of the xy plane tether in the orbital coordinate system
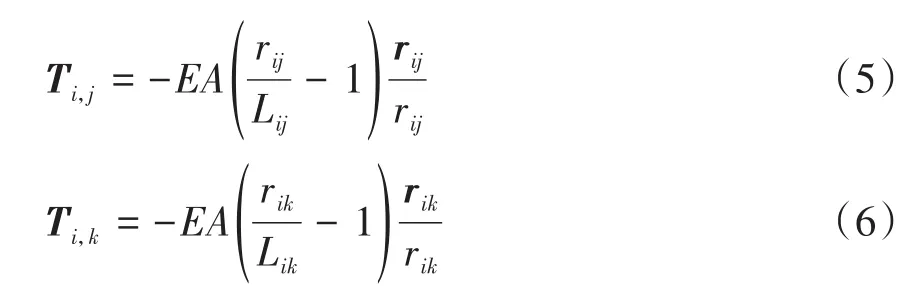
其中,E为系绳的杨氏模量,A为系绳的横截面积,rij及rik分别是卫星Si与Sj、Sk之间系绳的实时长度,rij及rik分别为它们的模.
通过本体坐标系可以表示出系绳拉力对卫星Si质心的距离rTij及rTik,从而得到拉力力矩Nij及Nik:

将各个力与力矩通过转换矩阵转换到相应的坐标系下,代入公式(1),(2)中即可得到系统的动力学方程.
2 系统动力学响应
取一组参数数值研究该动力学模型动力学响应,设卫星质量相同,为100kg,记绳系卫星编队系统质心所在轨道距地高度为H=500km,地球平均半径为RE=6378km,地球引力参数μE=3.9885×1014m3/s2[16],则系统所在得轨道高度的绕地角速度为:

即轨道坐标系o-xyz相对于惯性系O-XYZ的公转角速度约为Ω=0.0011rad/s;根据坐标系的建立得知,轨道坐标系相对于系统质心的角速度也为Ω,且旋转方向以逆时针为正.记系绳初始长度皆为L=10km,且不计系绳质量,刚体为rc=1m的球体.本文研究的三体环形绳系编队系统绕轨道坐标系z轴自旋运动,在给定系统初始自旋角速度为ω=5Ω的情况下,进行系绳连接处位置不同时的动力学响应的讨论.
2.1 系绳连接处延长线经过质心
取系绳刚度EA=5×104N,首先,对于系绳连接位置过质心的简单情况进行数值模拟,此时没有系绳拉力引起的扭矩,同时系绳位置及万有引力位于x,y平面内,因此,x,y平面内刚体所受力矩为0,只有z方向的扭矩,且没有z方向的位移.因此仅对x,y平面上的动力学响应进行展示.得到仿真结果如图2所示,表示惯性系下系统运行轨迹,图2为轨道坐标系下卫星1的运行轨迹,得到完整规则圆形,对其进行细节观察,可以发现卫星围绕系统质心旋转五个周期,而且周期之间距离相差较小.
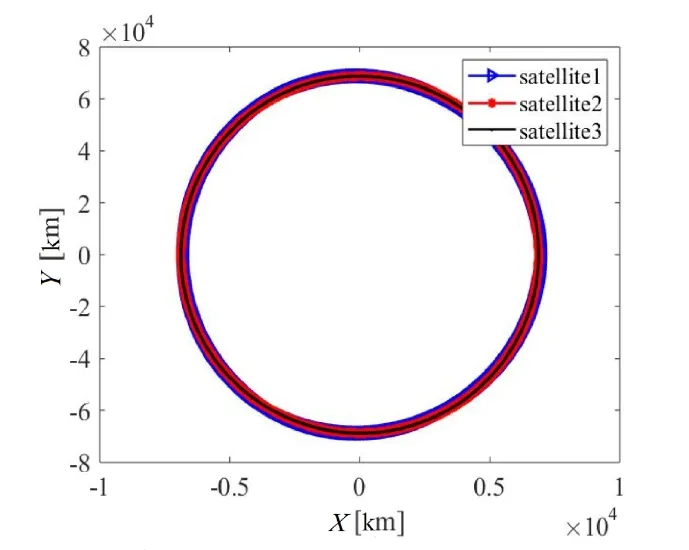
图2 惯性系下系统运动轨迹图Fig.2 Trajectory diagram of the system in the inertial coordinate system
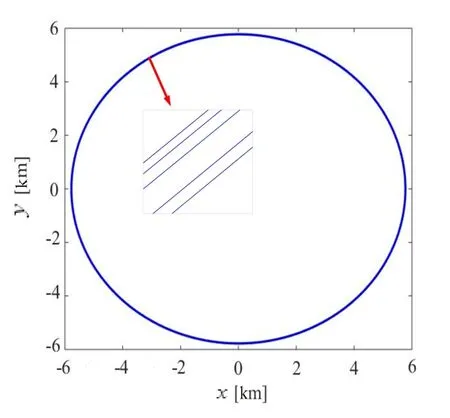
图3 轨道坐标系下卫星1运行轨迹Fig.3 Trajectory of satellite 1 in the orbit coordinate system
2.2 系绳连接处延长线不经过卫星质心
初始时刻,取系统质心及卫星S1的质心同时位于惯性坐标系O-XYZ的X轴上,卫星相对于各自本体坐标系的偏转角度都为0,数据模拟结果如图4,图5所示,图4表示惯性系下系统运行轨迹,图5为轨道坐标系下卫星1的运行轨迹,都得到完整规则圆形,因此表明系统是稳定的.同时观察轨道坐标系下卫星的运行轨迹细节,可以发现在ω=5Ω的情况下,卫星围绕系统质心转动五个周期,因此,验证了方法的正确性,但是相比于系绳位置穿过质心的情况,周期之间距离更大,受到系绳位置影响.

图4 惯性系下系统运动轨迹图Fig.4 Trajectory diagram of the system in the inertial coordinate system
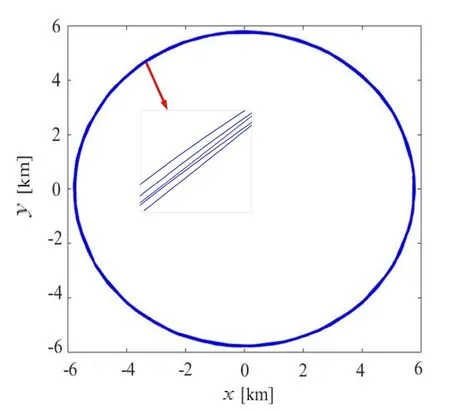
图5 轨道坐标系下卫星1运行轨迹Fig.5 Trajectory of satellite 1 in the orbit coordinate system
3 卫星姿态控制
3.1 基于单神经元自适应PID控制
首先通过转换矩阵,将卫星角度从四元数转化为欧拉角的形式,根据前文受力可知,卫星只受z方向的扭矩,因此只有绕z轴的转动,即α角的变化.单神经元自适应PID控制的结构框图如图6所示 .图 中 ,x1(k)=e(k)-e(k-1);x2(k)=e(k);x3(k)=Δ2e(k)=e(k)-2e(k-1)+e(k-2);初始角度为0,即理想角度为0,e(k)为卫星瞬时角度αd(t)与理想角度α(t)的差值.则控制律u(k)为:
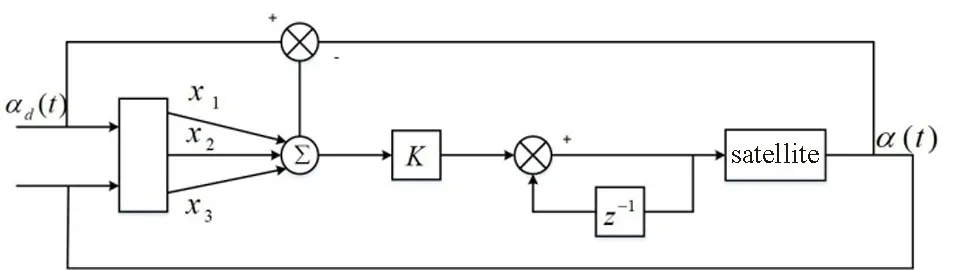
图6 单神经元自适应PID控制结构框图Fig.6 Single neuron adaptive PID control structure block diagram
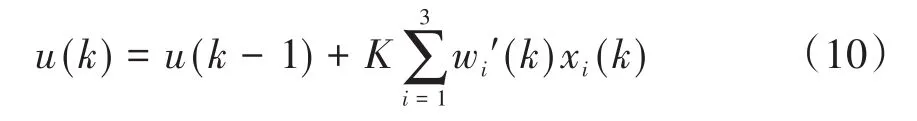
权值wi(k)的学习算法为:
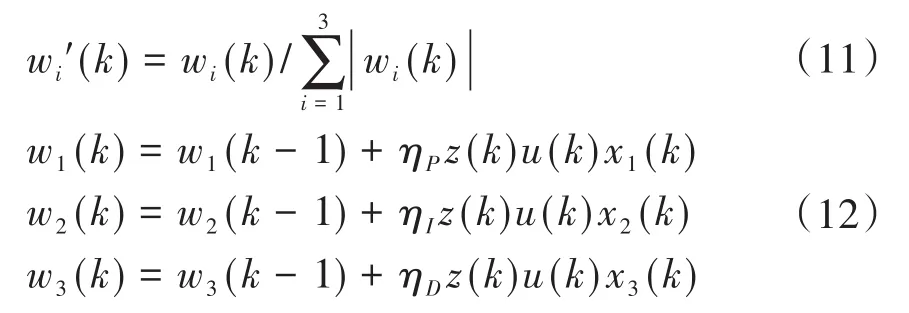
其中,z(k)=e(k);ηP、ηI、ηD分别为比例、积分、微分的学习速率;K为神经元的比例系数,K>0.对比例P、积分I、微分D的调节,可以通过ηP、ηI、ηD分别进行调节,取ηP、ηI、ηD分别为10、1、10进行计算,得到最佳比例、积分、微分系数.
3.2 滑模控制
通过滑模控制控制卫星角度α变化,考虑被控对象

取滑模函数为

其中,e(k)仍为卫星瞬时角度αd(t)与理想角度α(t)的差值,ė(t)为卫星瞬时角速度α̇d(t)与理想角速度α̇(t)的差值,则:
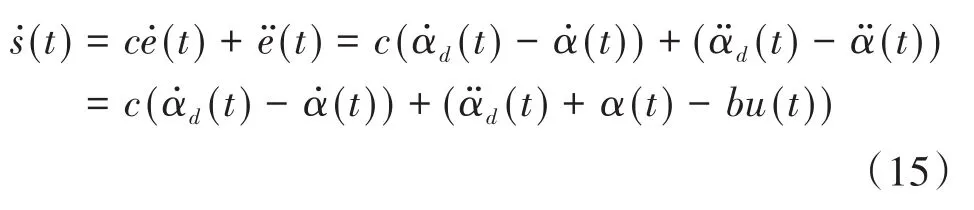
采用等速趋近律,有

结合式(16)和式(17),得基于趋近律得滑模控制律为:

取b,c,ε分别为1,100,0.01进行滑模控制.
3.3 算例研究
取前文的各数值进行控制仿真,如表1所示.

表1 绳系卫星系统参数Table 1 Parameters of tethered satellite system
对卫星1的姿态控制进行仿真,其他两卫星姿态控制方法类似.系绳连接处所在位置如图7所示,系绳延长线不经过卫星质心,首先通过普通PID控制,检验控制方法可行性,如图7所示.
由图7可以看出,在简单的PID控制下,卫星的姿态得到了良好的控制,说明控制方法的有效性,但是对于PID控制,控制参数需要通过经验以及多次实验得出,增加工作量,同时效率较低,因此通过改进方法,采用基于单神经元的自适应PID控制进行卫星的姿态控制.得到基于单神经元的自适应PID控制与PID控制结果对比图如图8所示.图中虚线为普通PID控制,实线为单神经元自适应PID控制,可以看出,单神经元自适应得到的PID的参数进行控制后,控制曲线超调量更小,控制效果更好,稳定速度更快.普通PID控制可以使卫星角度转动控制在10-2的数量级,而单神经元PID将其控制在0左右.
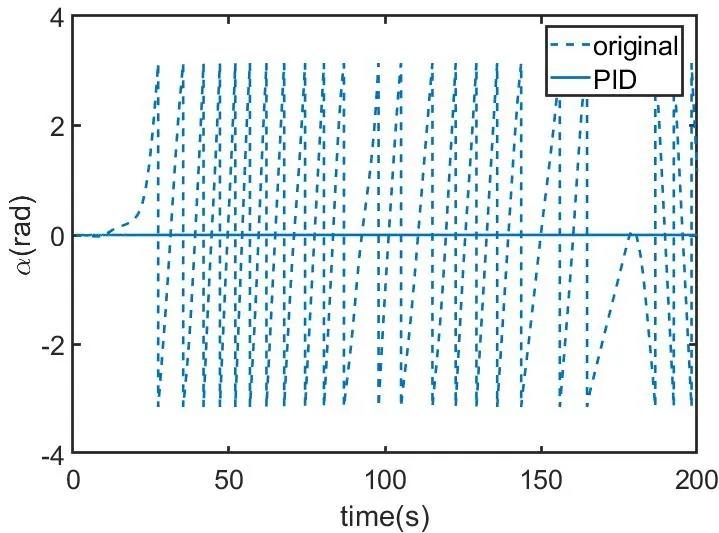
图7 有无控制卫星姿态对比Fig.7 Satellite attitude comparison:with vs.without control

图8 单神经元自适应PID控制与PID控制结果对比图Fig.8 Comparison of single neuron adaptive PID control and PID control results
对于滑模控制,控制结果与基于单神经元的自适应PID控制的对比图如图9所示.图9中实线代表单神经元自适应PID控制结果,虚线代表滑模控制结果.从图中可知,二者超调量基本相同,都可以达到10-4数量级,滑模控制响应更快,更加平稳,控制时间在10s左右,三种控制结果对比如表2所示.
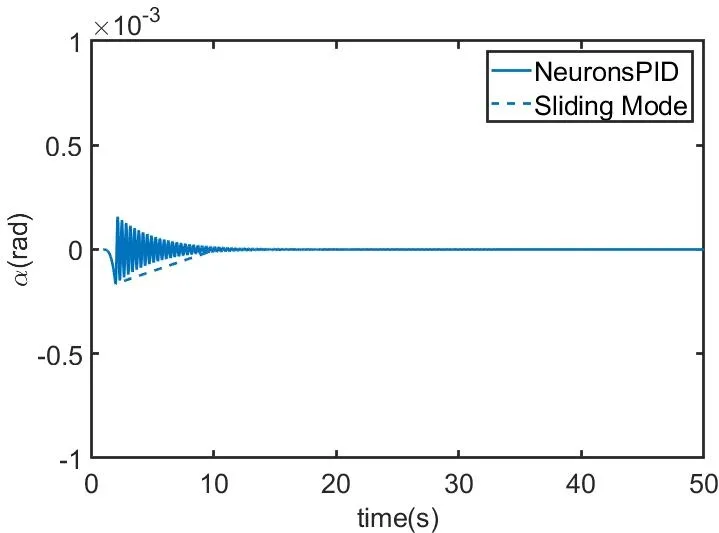
图9 单神经元自适应PID控制与滑模控制结果对比图Fig.9 Comparison of results of single neuron adaptive PID control and sliding mode control

表2 控制结果对比Table 2 Comparison of control results
4 结论
对于三体绳系卫星编队系统,通过采用考虑刚体姿态的模型进行动力学建模,获得更符合实际情况的动力学模型,得到不同系绳连接位置的动力学响应,验证模型有效性;对于系绳拉力引起的姿态不稳定,通过基于单神经元的自适应PID控制以及滑模控制进行姿态控制,并取得良好的控制效果.

