例析隐零点问题的解决策略

安徽省宣城中学 (242000) 张绪根

利用导数解决函数综合问题已经成为高考压轴题的命题趋势.这类问题最终都会转化为对函数单调性的判断，而函数单调性又与导函数的零点有密切的联系.但是在求解导函数零点时往往会遇到超越方程，无法直接求出，我们称之为导函数的隐零点.本文将介绍几种有效的处理策略.

一、直接观察

例1 已知(x2-x)lnx-ax≥0恒成立，求实数a的取值范围.

评注：对于比较简单的超越方程，我们可以采取特殊值试探出方程的一个根，再通过二次求导或者分类讨论证明解的唯一性.

二、虚设零点

由于题目的超越方程猜不出具体零点，我们需要退而求其次，虚设零点，然后对零点所满足的代数式进行合理变形与代换，将超越式化为普通式.

例2 设f(x)=ax+lnx+1,若对任意的x>0,f(x)≤xe2x恒成立，求a的范围.

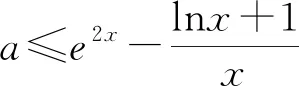
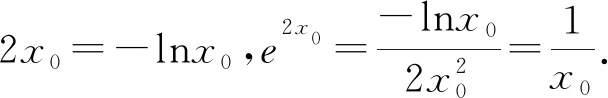
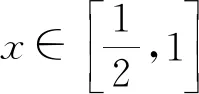
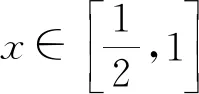
评注：上述两例的导函数均为超越函数，零点无法求出.采用虚设零点并利用零点存在性定理缩小其范围，接着通过ex0与lnx0的关系逐步将超越式简化为简单函数，这需要一定的代数变形与运算能力.

三、灵活放缩

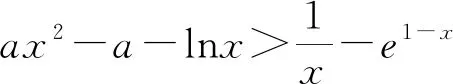
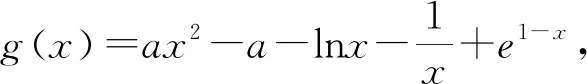
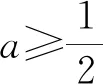
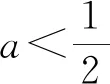
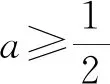
四、分离函数

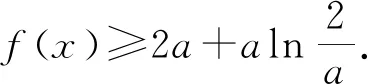
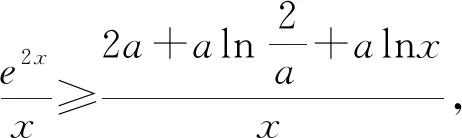
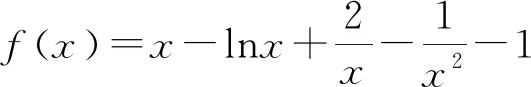
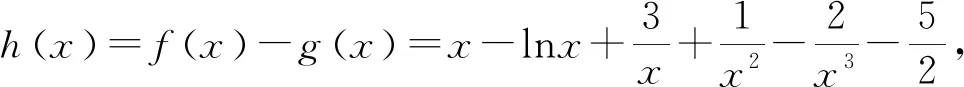
评注：当函数比较复杂时，可以采用分离函数转化为两个易于研究的函数.这类问题有一个典型特征，即可以证明g(x)min≥h(x)max，从而得出g(x)-h(x)≥0.

五、结束语

隐零点问题在高考中频率之高、地位之重必须引起我们的重视.解决这类问题，我们要尽可能把指数与对数分开，通过虚设零点、限制范围、整体代换，将复杂函数转变为简单函数.放缩法和分离函数法给解题提供了快速便捷的思路，具有一定的技巧性，平时多归纳一些常见不等式和简单函数图像对于我们解题大有裨益.