边缘轮廓上基于CPDA的图像角点检测
白萌萌,景军锋,章为川,孙久锐
(西安工程大学 电子信息学院,陕西 西安 710048)
0 引 言
角点是图像极其重要的局部特征,主要应用于图像处理及计算机视觉领域。角点检测是计算机视觉中一个极其重要的任务[1],主要应用于目标识别[2]、图像配准[3]、三维重建[4]等。角点可以定义为具有低自相似性的点,也可以定义为图像强度在大多方向上显著变化的点[5]。同时角点也可以定义为边缘轮廓上局部曲率极大值点或轮廓方向上急剧变化的点[6]。根据定义,现有的图像角点检测方法大致可分为3类:基于灰度的方法,基于模板的方法和基于轮廓的方法。
基于灰度的方法是通过分析图像像素值及像素之间的灰度变化直接从输入图像中提取角点。文献[7]在Moravec算法的基础上提出了经典的Harris角点检测算法,该算法通过局部自相关矩阵来构建角点响应函数(corner response function,CRF)。文献[8]提出了一种基于多方向多尺度结构张量积的图像角点检测算法。文献[9]用二阶广义(各向同性和各向异性)高斯方向导数滤波器得到不同角点的解析表达式来检测角点。
基于模板的方法是通过比较图像块和预先定义好的模型的匹配程度来检测角点。文献[10]提出 最小核值相似区(smallest univalue sengment assimilating nucleus,SUSAN)算法。该算法采用一种近似圆形模板,模板内部每个图像像素点和模板中心像素点的灰度值作比较进而检测角点。文献[11]用各向异性高斯方向导数滤波器[12]推导得到L型、Y型、X型和星形的角点解析表达式来检测角点。
基于轮廓的方法通过边缘检测器从输入图像中提取边缘特征,并分析轮廓上像素点的曲率信息来检测角点。曲率尺度空间技术(curvature scale space,CSS)[13]广泛用于基于轮廓的方法。首先用多尺度高斯滤波器平滑曲线,然后计算光滑曲线上每个点的曲率,将多尺度空间下的曲率极值点作为最终角点。但现有的CSS角点检测器对曲线上的局部变化和噪声非常敏感,且不容易选择合适的高斯尺度因子[14]。为了解决上述问题,文献[15]提出了CPDA离散曲率估计技术,它不涉及任何曲线点位置的导数,也不需要选择合适的高斯尺度因子。文献[16]提出利用平面曲线梯度相关矩阵 (gradient correlation matrices,GCM)进行角点检测,只需计算平面曲线的一阶导数,降低噪声影响。文献[17]基于Gabor滤波器虚部对边缘轮廓上像素点在多方向的幅值响应检测角点,提高了角点的检测精度、定位精度和噪声鲁棒性。还有许多其他技术,主方向角度差[18]、三角形理论[19]、拉普拉斯尺度空间[20]、边缘轮廓上基于近似离散曲率计算(approximation discrete curvature calculation,ADCC)[21-22]的角点检测方法。文献[23]提出基于多尺度曲率乘积技术(multi-scale curvature product,MSCP)的角点检测算法,该算法可以增强角点的曲率,抑制噪声,并且可以提高角点的定位精度。
CPDA离散曲率估计技术没有考虑如何准确检测相邻角点。 文献[24]提出了一种新的角点离散曲率解析表达式,分析了其在END、STAIR和L等3个角点模型上的曲率特性并以此来检测角点,发现CPDA角点检测算法中弦长的设定无法准确检测相邻角点,导致在有噪声的情况下检测结果优于无噪声。现有的基于CPDA的角点检测方法主要存在3个问题:①无法准确检测相邻角点;②难以选取3个合适的弦长;③角点检测速度较慢。
为了解决上述问题,利用参数对比实验得到一个可以准确检测相邻角点的弦长,然后选择该弦长对应的角度阈值,候选角点通过与曲率阈值和角度阈值比较去除弱角点和假角点得到最终角点。
1 角点检测算法
1.1 算法原理
CPDA角点检测算法中因3个弦长的选取在面对不同的检测情况时具有一定的随机性,更加剧了CPDA角点检测算法的检测性能不稳定性,而且其在运行时间上要慢于经典的角点检测算法。为克服CPDA角点检测算法因3个弦长选取而导致的检测性能不稳定,本文提出利用单一弦长进行角点曲率估计。首先利用大量参数选择对比实验,借助漏检点数、偏移量、误检点数、正确角点数作为评判依据,对CPDA角点检测算法进行单弦长的选取,结合相对应的最佳角度阈值与曲率阈值,进行角点的判断,如图1所示。
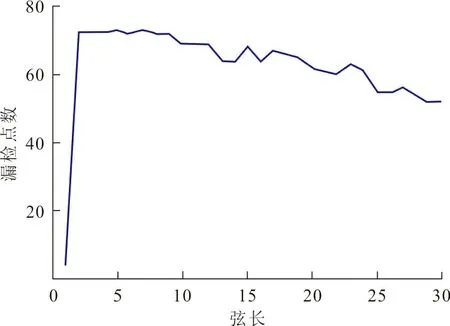
(a)漏检点数
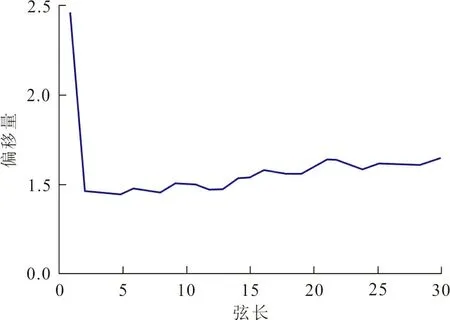
(b)偏移量
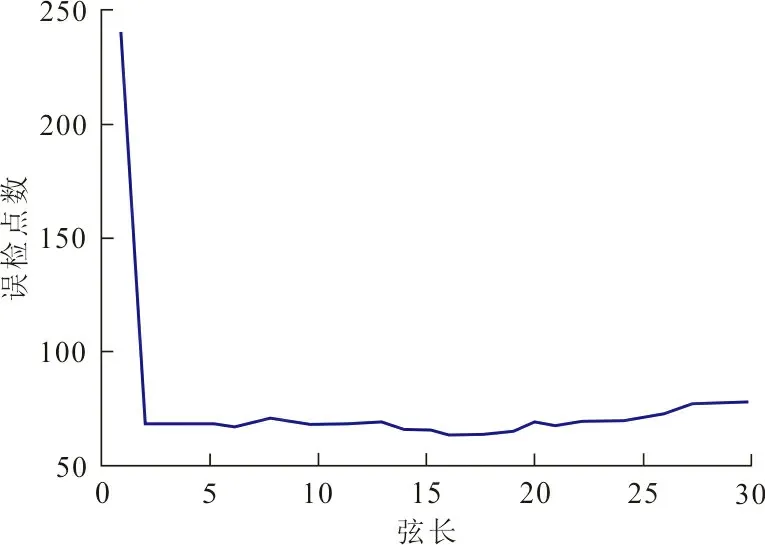
(c)误检点数
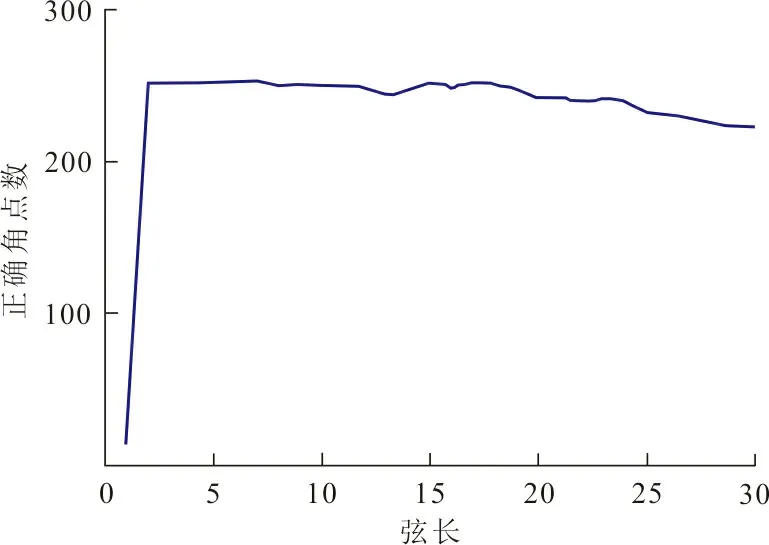
(d)正确角点数图 1 弦长选择Fig.1 Chord length selection
图1中,利用曲率阈值在0.00∶0.01∶0.35;弦长在1∶1∶30;角度阈值在135∶1∶190三者同时变化的60 480个数据的实验下得到的基于不同弦长的CPDA角点检测算法的检测性能比较,经过综合分析,弦长13为选择的最优弦长。该弦长在图1(a)和图1(c)中在漏检点数和误检点数上具有竞争优势,并且在图1(b)中定位偏移量也是极小,故该弦长是可以准确检测相邻角点的最佳弦长,与该弦长相对应的角度阈值为161o。本文提出的角点检测算法的步骤如下:
1) 利用Canny边缘检测器从边缘图像中提取边缘曲线,并且用小尺度高斯核平滑曲线,以此来消除量化噪声和琐碎细节;
2) 使用最优单弦长,将该弦长通过曲率计算公式进行曲率估计,获得曲线上各像素点的曲率;
3) 利用曲率阈值,与所得曲线上各像素点的曲率进行比较,若该像素点的曲率大于曲率阈值,则记为候选角点;
4) 曲线上某些直线部分像素点的曲率会大于曲率阈值,会造成角点的误检。因此再利用角度阈值进行判断,若候选角点的角度大于角度阈值,则将该候选角点去除,得到最终角点。
1.2 Canny阈值设置
选取Canny边缘检测器的高低阈值时,考虑到阈值过高会使提取到的边缘信息变少,阈值过低则会检测到虚假边缘,因此选取灰度图像Block图和Lab图,其标准角点数分别为59、249,在[0.00,1.00)设置8个区间对其检测,进行Canny边缘检测器的阈值选取。通过检测的正确角点数、误检点数、偏移量、漏检点数和运行时间来选取最合适的阈值,检测结果如表1、2所示,其中“—”代表数据无意义。

表1 不同阈值对Block图角点检测的准确性指标Tab.1 The accuracy index of different detectors for Block image corner detection
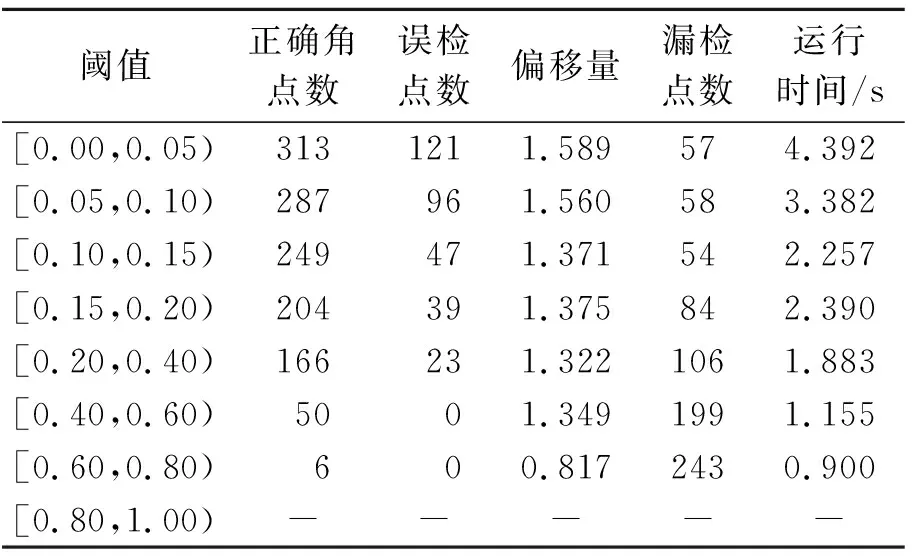
表2 不同阈值对Lab图角点检测的准确性指标Tab.2 The accuracy index of different detectors for Lab image corner detection
从表1、2的检测结果综合分析得出,在Canny阈值取值不同时,对灰度图像Block图、Lab图的检测结果差别较大。其中阈值为[0.10,0.15)时,2幅灰度图像的检测的正确角点数最接近标准角点数,且误检点数、偏移量、漏检点数,运行时间在[0.00,1.00)的8个取值区间中综合性能最佳,因此本文选取Canny边缘检测器的阈值为[0.10,0.15)。
2 实验结果与分析
实验是在计算机配置为Intel(R) Xeon(R) Gold 5118 CPU @ 2.30 GHz处理器、128 GB内存的Windows平台上基于Matlab编程实现。对比分析中,Canny边缘检测器的阈值设置为[0.10,0.15),最优单弦长为13,角度阈值为161°。
为了进一步比较这5种检测器对灰度图像检测的优劣,将正确角点数、误检点数、偏移量、漏检点数和运行时间作为评价指标,分别选用本文提出的算法检测器、FAST检测器[25]、GCM检测器[16]、ANDD检测器[11]和CPDA检测器[14],选取2幅具有标准角点数的灰度图像:Checkerboard 图和Lab图,对其进行角点检测,其标准角点数分别为48、249。检测结果分别如表3、4以及图2所示。其中表3、4是不同检测器分别对Checkerboard图、Lab图角点检测的准确性指标,图2是不同检测器下对Checkerboard图、Lab图的角点检测结果。
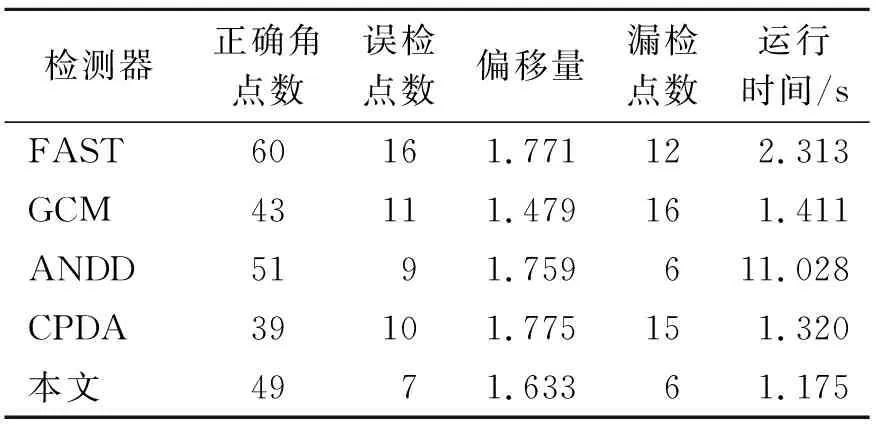
表3 不同检测器对Checkerboard图角点检测的准确性指标Tab.3 The accuracy index of different detectors for Checkerboard image corner detection
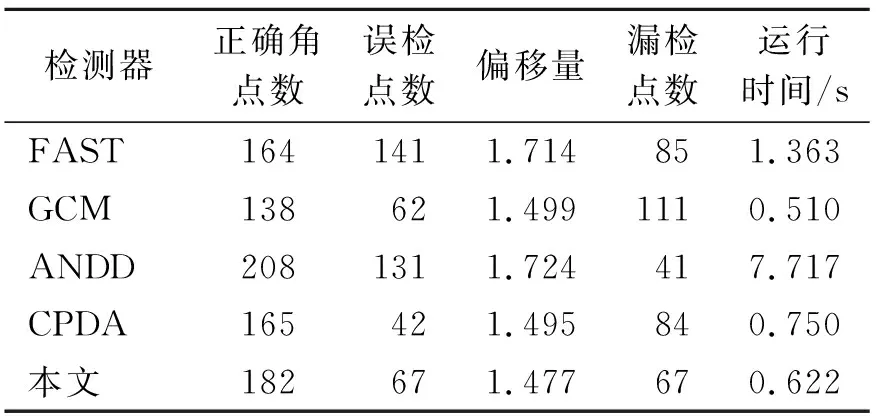
表4 不同检测器对Lab图角点检测的准确性指标Tab.4 The accuracy index of different detectors for Lab image corner detection
对表3和图2(a)的检测结果分析,本文算法检测器检测的正确角点数49个,是所有检测器中最接近标准角点数48的检测器。而且其误检点数、运行时间都优于其他4种算法检测器。本文算法检测器的漏检点数与ANDD检测器相同,但运行时间仅有1.175 s远远低于ANDD检测器的11.028 s。综合表3和图2(a)的数据分析,对于Checkerboard图的检测,本文算法检测器的性能最佳。
从表4和图2(b)的检测结果分析得出,本文算法检测器的偏移量在本文比较的检测器中最低,运行速度仅次于GCM检测器,但漏检点数远低于GCM检测器,并且正确角点数仅次于ANDD检测器,检测准确率较高。本文算法检测器的误检点数远低于ANDD、FAST检测器。综合表4和图2(b)的数据得出,对于Lab图的角点检测,本文算法检测器的综合性能最佳。

(a)Checkerboard图及其角点检测


(b)Lab图及其角点检测图 2 不同检测器对Checkerboard图和Lab图的角点检测结果Fig.2 The corner detection results of Checkerboard diagram and Lab diagram by different detectors
3 结 语
本文提出的算法针对CPDA角点检测算法的不足做出了改进。为实现角点的准确检测,利用大量参数选择对比实验下的最优单弦长和角度阈值检测角点。由实验结果可知,本文提出的算法检测器的检测精度要高于其他4个检测器,提高了角点检测的准确率和速度,相较于CPDA角点检测算法具有更好的检测性能,与现有的基于边缘轮廓的角点检测算法相比,具有更好的角点检测准确率和稳定性。这为目标的重建、跟踪、识别等处理奠定了基础,具有广泛的应用前景。

