数形结合:数与形的双向“沟通”
无言

数形结合,反映了图形与数量之间的关系。既是重要的知识内容,又是重要的数学思想。
两条直线的位置关系与角的大小之间有着内在联系。由角的数量关系判定直线的位置关系,由直线的位置关系决定角的数量关系。
例如,两条直线相交就一定会产生角——两组对顶角,因为两组对顶角分别相等、两组对顶角之间互补,所以只要其中一个角确定,那么其他3个角就全部确定。因此,只要聚焦其中一个角即可。当这个角的大小是一个特殊值——90°的时候,这两条直线就垂直。于是,交角的90°判定了两条直线垂直,两条直线垂直就决定了交角的值为90°。这就是垂直概念的两层含义。
很自然地,我们会想:既然相交的位置关系是这样研究的,那么平行的位置关系是否也有类似的研究呢?
麻烦的是,对于什么是平行,课本上只给出了一个模糊的说法:“在同一平面内,不相交的两条直线叫作平行线。”什么是不相交呢?不相交就不产生交角。这只是一种直观的认识,在具体问题中无法像垂直一样进行清晰精确的操作。
但是,平行线的作图过程告诉我们,三角尺的平移保证了两条边的平行,如图1。
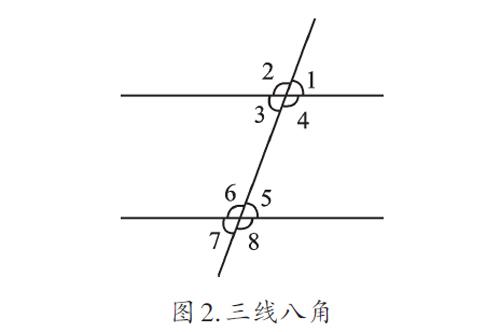
对这个过程进行抽象,就会出现两条直线被第三条直线所截的基本图形——三线八角,如图2。在这个图形中,兩个交点处共出现四组对顶角。根据前文内容,我们只需要在两个交点处分别聚焦一个角即可。
平行线的画图,让我们自然关注这些角:∠1与∠5、∠4与∠8、∠7与∠3、∠2与∠6,这四组角相对于截线和被截线而言位置都相同,因此叫同位角。画图也告诉我们一个基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。这就建立了第一个判定条件——由同位角的数量关系判定直线的位置关系。
进而,诸如∠3与∠5、∠4与∠6都是位于被截线内部、交错分布在截线两侧,因此名为“内错角”。内错角的数量关系可以化归为同位角的数量关系。同理,命名“同旁内角”,其数量关系同样化归为同位角的数量关系。所以,“三类角”的数量关系就判定了直线的位置关系。
在苏科版数学教材七年级下册第16页读一读《怎样证实“两直线平行,同位角相等”》中,编者依据基本事实“同位角相等,两直线平行”“过直线外一点有且只有一条直线与已知直线平行”,利用反证法,证实了“两直线平行,同位角相等”。这就构建了由直线的位置关系决定一类角的数量关系的方法。在此基础上,将另外两类角的数量关系化归为同位角的数量关系。于是,直线的位置关系就决定了“三类角”的数量关系。
可见,将直线的位置关系与“三类角”的数量关系建立联系,既是知识发展的必然逻辑,也是一种形象直观的方法。这种数形结合的思想不仅体现在知识的形成过程中,其重要性更体现在具体的解题过程中。
(作者单位:江苏省无锡市西漳中学)

