三阶线性自抗扰控制器的液压伺服流量控制

赵 爽， 史红伟， 刘小松， 李鹏程， 左 越

(1.长春理工大学电子信息工程学院,吉林长春 130022；2.长春水务集团城市排水有限公司西郊污水处理厂，吉林长春 130022)

引言

电液伺服系统由于具有功率质量比高、负载刚度大、有效载荷能力强、响应速度快等特点，被普遍应用在航空航天、武器装备、能源冶金、海洋设备、矿山机械等方面[1-3]。然而电液伺服系统是一类具有大范围复杂不确定性系统，本身存在多种非线性和时变因素[4]，导致电液伺服控制系统的动态、稳态特性很难达到较好的控制效果。如何抑制液压伺服系统未知非线性扰动，提升系统跟踪性能的同时抑制系统超调一直是研究人员关注的热点。

目前电液伺服系统的控制方法主要有：以PID、变结构滑模控制、反步控制为主的经典控制；以遗传算法、模糊控制为代表的智能控制；以扩张状态观测器为手段的自抗扰控制，三大类算法单独或相互配合控制。文献[5]采用对输入输出同时跟踪的双跟踪微分器，结合基于fal函数的非线性PID，解决了非对称液压缸在负载发生变化时产生的位移跌落和速度振荡，但对于系统响应的超调并未给出合理的解决办法。文献[6]对电液伺服变量泵执行机构采用 “大偏差大控制力，小偏差微控制力” 的分段非线性PI控制算法，解决了动态误差与控制器参数不匹配问题，降低了系统超调，但没有完全抑制，且动、静态都存在于非线性扰动引起的响应波动。

为克服PID算法在液压伺服系统上的控制局限，将其与神经网络[7]、模糊自适应[8-12]、遗传算法[13]等智能控制算法联合设计控制器，发挥PID控制优势的同时，配以智能控制算法弥补其不足。例如文献[14]为抑制水上液压电机的风速扰动引起的功率波动，采用模糊PID调节泵排量，从而得到最优的液压泵转矩，以更快的速度和更小的稳态振荡提供了更好的跟踪效果，抑制了来自风速扰动的功率波动。

滑模变结构控制由于在解决非线性参数摄动问题上具有独特优势而被广泛应用于液压伺服系统控制中。文献[15]通过设计一种光滑连续一阶可导的滑模控制率并结合反步递推控制算法，很好地解决了滑模与反步控制算法间的设计冲突，有效抑制了阀控电液伺服系统未知匹配干扰和输出抖动；文献[16]采用高阶滑模微分器观测系统未知状态，在控制器中引入描述系统响应的指标函数，获得较PID算法更快的跟踪速度和更好的稳态性能。然而滑动超平面的选取和等效控制率的设计增加了控制器的设计难度。

基于扰动观测器对系统未知状态的估计作用，将状态观测器与其他控制策略相结合，对液压伺服系统取得了一定的控制效果。文献[17]为解决液压子系统间的强耦合作用，提出了基于反步滑膜鲁棒控制和状态观测器的复合非线性解耦控制率，消除了位置跟踪子系统和速度平滑子系统间耦合作用对系统响应的干扰，实现了系统的跟踪控制和速度的平滑调节，提高了系统的鲁棒性和协调性。文献[18]为解决单杆电液伺服系统未知状态较多，且能量利用率较低的问题，利用状态观测器估计系统未知状态，提出了一种基于非线性扰动观测器与输出反馈相结合的控制器，提高了系统的跟踪精度和能量利用率。文献[19]为消除系统动力学非线性对输出响应的干扰，利用泵控液压系统的等效非自治模型，对动力学中影响控制性能的集总未知项作为扩张状态，提出了一种先进的高阶扰动观测器，并进一步结合鲁棒滑模控制，设计了先进位置控制器，使系统在有界时变干扰下，提升了系统响应的渐近跟踪性能。

由于ADRC算法无需预知被控对象模型，能够同时抑制被控系统内、外的线性或非线性未知干扰，被广泛用于解决液压伺服系统输出扰动问题。文献[20]为减小因扩张状态观测器产生的相位滞后，提高系统响应速度，设计了一阶ADRC与位置反馈闭环相结合的控制器，提升系统响应速度的同时抑制了非线性扰动。文献[21]为消除电液负载敏感伺服系统中阀控子系统与泵控子系统间的强耦合作用，设计二阶位置ADRC和一阶压力ADRC，有效地消除子系统间的强耦合。然而由于ADRC涉及非线性函数，导致参数较多且整定复杂，难以单独在工控领域得到广泛应用，迫切需要一种能实现ADRC控制效果，且参数较少、整定办法简单的控制策略。

为解决ADRC参数整定困难，LADRC被广泛研究与应用。文献[22]推导并验证了高阶LADRC基于李亚普诺夫意义下的稳定性，实现三阶LADRC对非线性的一级倒立摆系统的控制，减少整定参数的同时获得了较ADRC更快的跟踪速度和超调抑制能力，为LADRC在非线性系统上的工控应用提供了理论支撑和算例验证。

为进一步提高液压伺服系统的控制性能，提出将高阶LADRC控制策略应用于非线性的液压伺服系统，基于三阶LADRC结构和基于控制器带宽的线性误差反馈控制率参数整定办法，通过将跟踪误差前馈与扰动估计反馈相分离的控制器结构，设计了一种改进的三阶LADRC算法。通过对比传统三阶LADRC、PID算法和改进的三阶LADRC对被控对象模型仿真分析，验证了改进的三阶LADRC算法在扰动抑制、克服超调等方面更具有优势，为一类三阶大范围不确定液压伺服系统的控制研究提供了有力的参考。

1 系统数学模型

液压伺服阀控系统组成如图1 所示，主要包括控制器、电液伺服阀、液压马达、负载及进出口油液压力传感器，通过测量液压马达出口流量，构成闭环反馈。

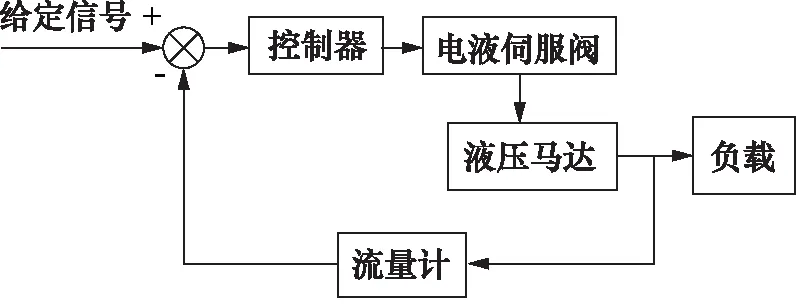
图1 液压伺服阀控系统组成

阀控液压马达作为一种常用的液压动力元件，建立滑阀的流量方程、 液压马达流量连续性方程及液压马达和负载的力平衡方程3个基本方程[23]，对应的3个拉氏变换分别如式(1)～式(3)：

QL=KqXv-KcpL

(1)

(2)

pLDm=Jts2θm+Bmsθm+Gθm+TL

(3)

式中,QL—— 伺服阀负载流量

Kq—— 伺服阀流量增益

Xv—— 伺服阀阀芯位移

Kc—— 伺服阀流量压力系数

pL—— 液压缸负载压降

Dm—— 液压马达的排量

θm—— 液压马达的转角

Ctm—— 液压马达的总泄漏系数

Vt—— 液压马达两腔及连接管道总体积

βe—— 液压油有效弹性模数

Jt—— 液压马达和负载折算到马达轴上的总惯量

Bm—— 液压马达和负载的黏性阻尼系数

G—— 负载的扭转弹簧的刚度

TL—— 作用在马达上的任意外负载力矩

联立式(1)和式(2)消掉QL得pL，如式(4)：

(4)

式中,Kce是总流量压力系数，如式(5)：

Kce=Kc+Ctm

(5)

将式(5)带入式(4)后，再带入式(3)得到式(6)：

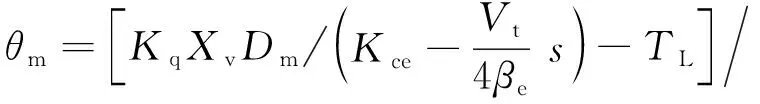
(6)

设液压固有频率ωh如式(7)，液压阻尼比ξh如式(8):

(7)

(8)

基于被控系统的实际情况，给出以下合理假设：

(1) 负载的扭转弹簧的刚度G=0；

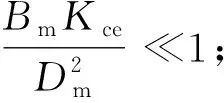
(3) 负载黏性阻尼系数Bm很小。

将式(7)、式(8)带入式(6),并经合理化简得到液压马达转角方程式(9)：

(9)

进一步得到液压马达轴的转角对外负载力矩的传递函数，如式(10)：

(10)

液压马达轴的转角对阀芯位移的传递函数如式(11)：

(11)

带入系统辨识参数得到系统开环传递函数如式(12)：

(12)

可见该液压伺服流量开环系统是一个高增益，三阶且不可降阶，阻尼系数较小，同时包含一阶积分与二阶震荡环节，且3个极点距离较远的复杂被控对象。

2 三阶LADRC设计

针对一类高阶不确定非线性SISO系统，传统LADRC方案，包含线性跟踪微分环节(LTD)、线性扩张状态观测器(LESO)和线性误差反馈控制率(LSEF)三部分。

2.1 线性跟踪微分环节

该环节是对系统输入的跟踪及其一阶、二阶微分，即通过提取输入信号的位置、速度和加速度等动态特征实现给定输入的平滑过渡。本质上该环节也是一种扩张状态观测器，除对给定输入的跟踪、及其一阶、二阶微分这3个状态外，还扩张了第4个状态用于估计跟踪微分器的误差。对于频繁改变给定输入信号的被控系统，尤其是采用“利用偏差消除偏差”的控制策略时，跟踪微分环节是抑制系统超调的有效方法。

三阶线性跟踪微分器如式(13)：

(13)

式中,v0为给定输入信号；R为跟踪速度调节因子，R值越大对输入信号的跟踪能力越强，在文献[18]中给出了基于李雅普诺夫的系统收敛性的证明，R值并不能无限大，通常在(10,50)区间内进行参数调节即可满足跟踪性能要求。

2.2 线性扩张状态观测器

作为自抗扰控制算法的核心环节，扩张状态观测器结合现代控制理论中的观测器与扰动估计技术，将开环系统响应中异于观测标准型的部分全部视为扰动并反馈消除。

线性扩张状态观测器对非线性系统具有较好扰动估计和标准化改造效果，考虑控制器在工程实践中的可实现性与参数整定的难易程度，本研究采用基于观测器带宽参数整定的LESO，算法如式(14)：

(14)

设ωo为观测器带宽，则根据极点配置法如式(15)：

(s+ωo)4=s4+β1s3+β2s2+β3s+β4

(15)

则LESO的参数可由观测器带宽按式(16)给出：

(16)

2.3 线性误差反馈控制率

在LADRC中，LESF最为常用的是基于控制器带宽ωc进行参数整定的PD组合形式。在二阶控制器中这种反馈控制率可以理解为：对输入信号的跟踪v1与对输出信号的跟踪z1间的偏差作为比例控制的输入；通过输入跟踪信号的一阶微分v2与输出跟踪信号的微分z2间的偏差，作为自带微分作用的输入信号，经简单的放大或缩小实现微分控制。然而在三阶LADRC中，随着控制器的阶数提高，相对于二阶LESO，三阶LESO中增加了对输出跟踪信号的二阶微分信号，该信号反映了系统输出的变化趋势，为与之相匹配，在2.1节LTD的设计中也包含了对输入信号的二阶微分v3。

大多LADRC设计并没有引入TD的跟踪误差，这在给定输入基本不发生大范围变化时是可行的，但对于需要频繁改变给定输入流量的工程需求，引出输入信号的跟踪误差是十分有必要的，因为LESO本质上观测的是控制输入u与系统输出间异于标准型的总扰动，并不包含对输入信号的跟踪误差，增设一路反馈汇总两者作用，在控制输入前抵消掉汇总后的扰动，实现真正意义上的总扰动补偿。

线性误差反馈控制率设计如式(17)：

u=a1e1+a2e2+a3e3+a4e4

(17)

式中，ei=vi-zi，i=1,2,3,4。

2.4 三阶LADRC结构

综合上述各环节设计，三阶LADRC结构如图2所示，其中b0为控制器增益。

图2 三阶LADRC结构

2.5 LESF参数整定方法

为使参数整定办法具有普适性，在分析参数对系统响应的影响时，应选择较为典型且包含一阶积分环节的三阶系统，如式(18)：

(18)

按照本节的设计，在Simulink中构建如图3所示的三阶LADRC。

按文献[22-24]给出的2种LESF参数整定办法分别如式(19)和式(20)：

a1=a4=1，a2=a3=3

(19)

(20)

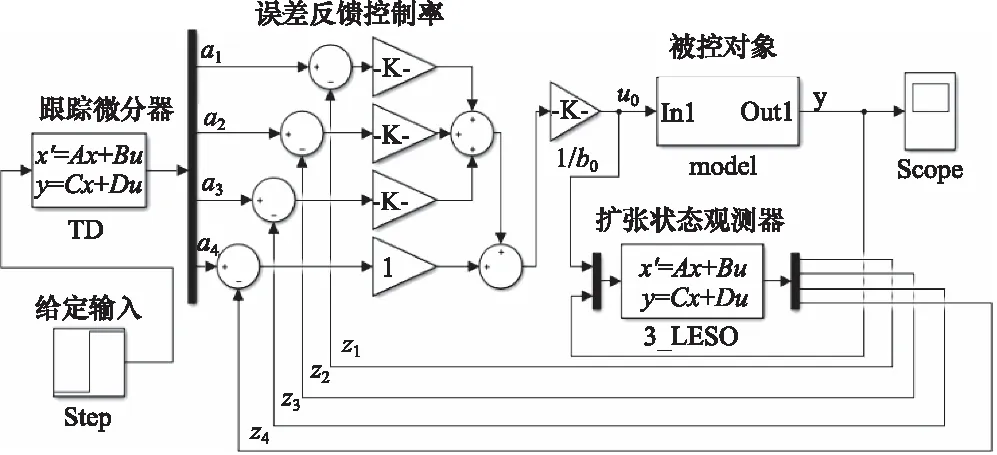
图3 基于Simulink搭建的控制器仿真结构

并取ω0=300,b0=30,R=50，ωc=10，系统输出响应如图4所示。

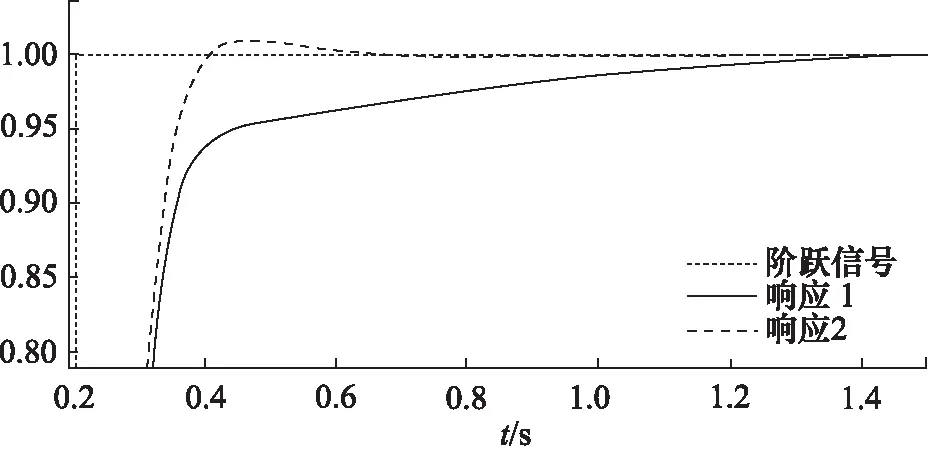
图4 LESF参数选取

2种反馈控制率都能够很好的抑制未知扰动，尽管都存在一定的超调，但后者在跟踪速度和稳态性能上较前者具有明显优势。综上，选择基于控制器带宽参数整定的误差反馈控制率。

2.6 改进的LADRC扰动反馈结构

在2.1节中已明确指出LESF的第4个状态v4是对跟踪误差的估计值，直接将其与系统总扰动估计值按1∶1比例在控制输入前分别进行前馈、反馈补偿。然而在仿真参数调节过程中发现v4前馈增益的大小对系统超调影响较大，可以缓解系统快速性和超调之间的矛盾。为了验证该结论，先将跟踪误差的前馈和总扰动估计的反馈补偿分离，构成如图5所示的控制器结构，并通过改变a4值的大小改变跟踪误差的前馈增益，仿真结果如图6所示。

当a4在[0.9,1.2]内逐渐递增时，在保证系统跟踪的快速性和静态响应基本一致的同时，系统超调量逐渐下降。至此，三阶LADRC改造完成。

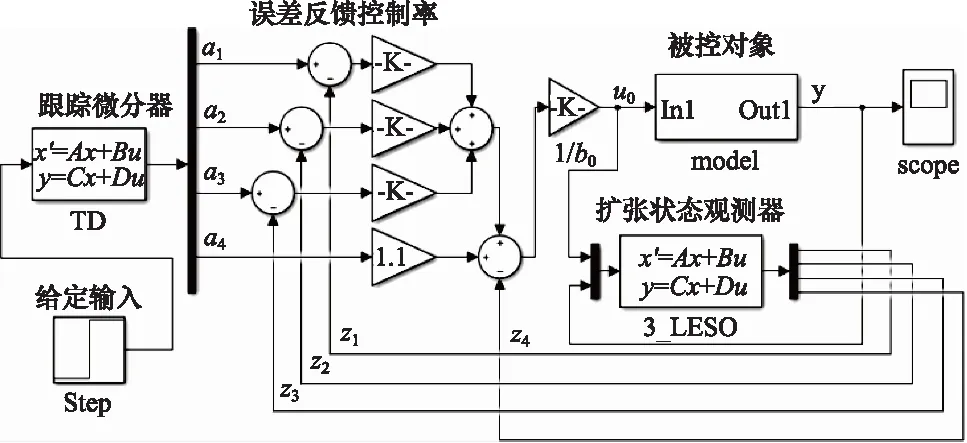
图5 改进的三阶LADRC结构

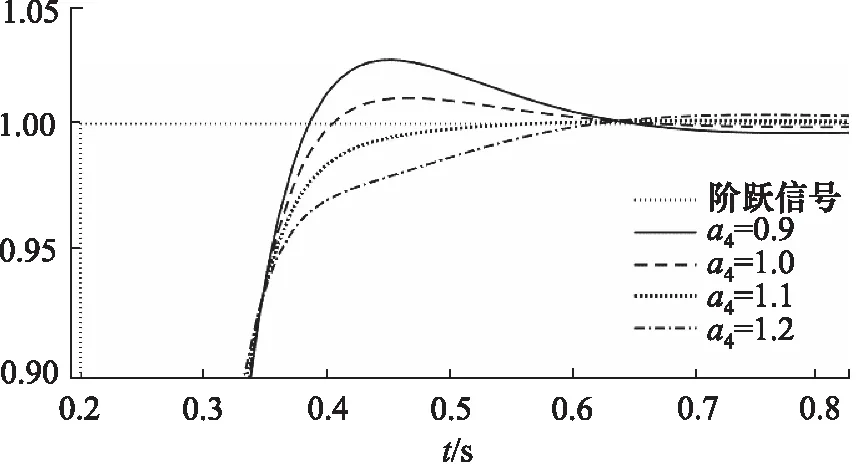
图6 跟踪误差前馈增益对系统响应的影响

3 仿真分析

在Simulink中搭建系统开环模型，分别采用PID控制、传统的三阶LADRC(结构如图3所示)和改进的三阶LADRC(结构如图5所示)对其进行仿真分析。

传统LADRC参数：a1=a4=1，a2=a3=3，w0=1000，b0=4.5988e5，R=30；改进LADRC仿真参数：wc=500，w0=1000，a4=1.1，b0=4.5988e5，R=30；PID控制器参数：KP=0.6,KI=0,KD=0。

实验一：给定终值为1，起始时间为0.2 s的阶跃信号，系统内部附加幅值范围[-1,1]的随机噪声，添加位置如图7所示，仿真结果如图8所示。

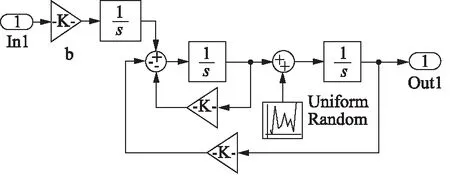
图7 随机噪声添加位置示意图

针对该类高增益复杂被控对象，传统的三阶LADRC不能获得满意的控制效果，且针对内外扰动复杂、扰动幅度较大的欠阻尼系统，在跟踪速度基本一致的情况下，PID算法将扰动抑制在20%范围内，改进的三阶LADRC算法有效的将扰动抑制在1%范围内，验证了改进的LADRC较PID算法具有更好的扰动抑制能力。

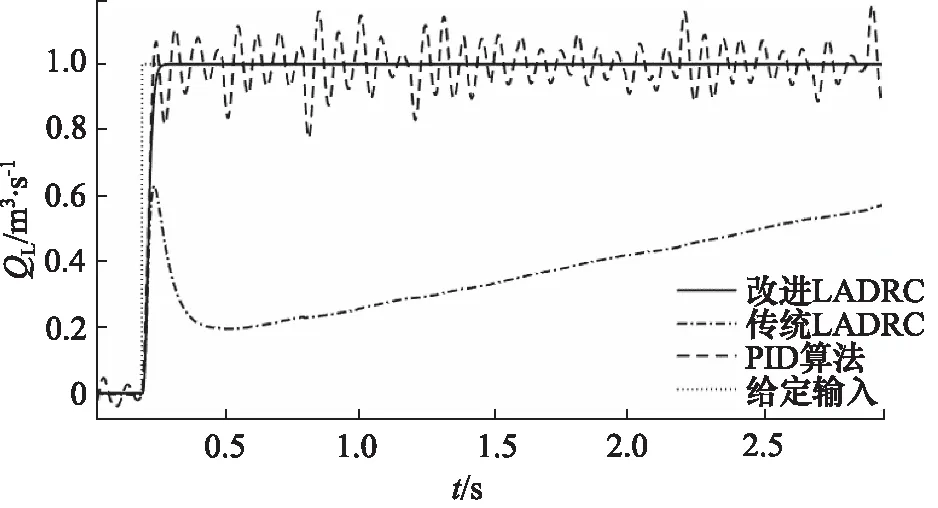
图8 阶跃输入下的系统响应

实验二：在0.2 s给定终值为1的阶跃输入，并在0.3，0.5，0.8，1.0 s增加终值分别为1，1，1，-2的阶跃输入，系统内附加噪声同实验一，仿真结果如图9所示。

图9 改变阶跃输入下的系统响应

在频繁改变阶跃输入时，PID控制算法存在一定的震荡、超调，尤其对于液压马达阀控系统这种开环增益较大的被控对象，超调会对系统造成一定的冲击和负担。在跟踪速度基本一致情况下，改进的三阶LADRC算法能够平稳无超调进入终值，验证了改进的LADRC具有较PID更强的抑制超调能力。

实验三：给定峰-峰值为1，频率为5 rad/s的正弦信号，系统内附加噪声同实验一，仿真结果如图10所示。

在给定正弦信号输入时，PID算法控制下的系统响应在峰值附近超调现象比较严重；改进的LADRC算法能够无超调、无静差的平滑跟踪给定的正弦信号，验证了改进的LADRC具有较PID更平稳的跟踪能力。

4 结论

通过将高阶线性自抗扰控制器的结构和传统LADRC的参数整定办法相结合，提出一种改进的三阶自抗扰控制器，既突破了高阶LESO对一类大范围不确定性非线性系统的控制局限，有效抑制未知扰动的同时又克服了PID算法在突变输入下产生的超调。经仿真分析与验证，针对液压伺服流量控制模型，改进的LADRC具有更强的扰动抑制能力和克服系统超调能力。

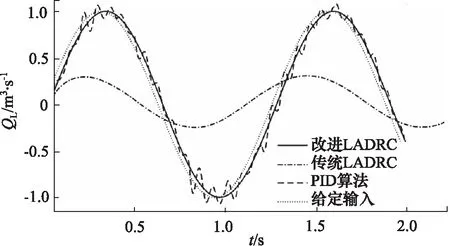
图10 正弦输入下的系统响应