合数母数素数母数在自然数中的分布图和应用
(内蒙古包头铁路公安处 内蒙古·包头 014040)
0 引言
本文简要介绍了母数论的思想。并在论文1①的基础上,再向读者介绍一种用图象法或说网络法,网尽勾股数的方法。同时告诉读者几种新的判定奇素数和合数的方法。通过论文1读者了解了母数的概念后,这篇论文3将在母数论的层面,描绘出素数母数合数母数在自然数中的分布图(也叫勾股数网络图)。
这个图反映了素数母数合数母数在自然数中的分布规律。只要首先掌握了合数母数在自然数中的分布规律,对素数母数的认识就一目了然了,进而求解素数,合数在自然数中的分布规律也迎刃而解了。
列举了网络图的3个应用:(1)判定奇素数和奇合数;(2)分解奇合数;(3)求网络勾股数②…指出网络图象魔方一样变化多样,远不止这三个用途。有兴趣的读者自可根据母数论思路去挖掘寻觅。
1 母数的定义和用途
定义1:我们把n叫做奇数2n+1的母数(n∈N),显然n和2n+1是一一对应的。
定义2:有奇合数M=2d+1,母数d叫做合数母数。d∈D(D是所有合数母数d的集合)。
定义3:有奇素数P=2p′+1,母数p叫做素数母数。p∈E(E是所有素数母数p的集合)。
由定义1、2、3有推论:d是合数母数,2d+1一定是奇合数。p是素数母数,2p+1一定是奇素数。
有了上面的定义,反过来,我们有时把奇数2n+1叫做其母数n的子数。显然,子数等同于奇数。就是说任何奇数或说子数2n+1都有一个母数n(后面的论文中要用到子数的概念)。
这样我们就会建立起子数(奇数2n+1)与其母数n,奇合数(2d+1)与其合数母数d,素数(2p+1)与其素数母数p′一一对应的关系:

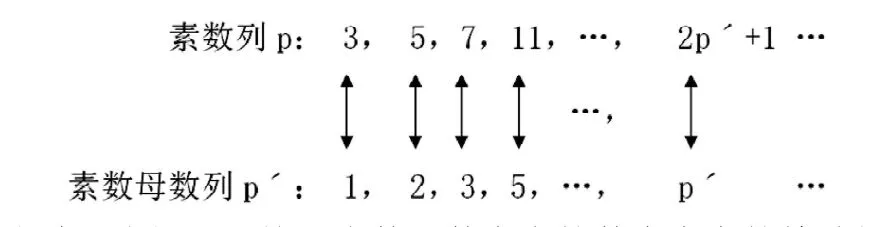
由此,我们可以按照合数母数在自然数中存在的特殊规律编织出一个能够网尽合数母数留下素数母数的网络之筛。同时,这个严密的网络之筛,同样能网尽勾股数。
2 素数母数合数母数在自然数中的分布图(也叫勾股数网络图)
我们讨论母数方程:d=x+y+2xy (x,y∈N,d∈D)
这是一个关于合数母数d的二元二次不定方程。合数母数d是由x,y在正整数范围内取值多少来确定的。我们知道解方程求X,Y的正整数解较难,反过来x,y取正整数求d易。读者在论文2③中已经见到过这种合数母数方程。
这种情况下,我们可以把合数母数d的变化拓展为一个依赖于(x,y)的函数。
定义:Zh(x,y)=x+y+2xy x,y∈N)为合数母数函数,它是一个关于x,y的二次函数。
这个函数的定义域我们只限定在正整数范围内取值:有x,y∈N 所以,
值域:D={d(x,y)∣Zh(x,y)=x+y+2xy d( x,y)∈D}
或 D={d∣d=Zh(x,y) d∈D}
在 d=x+y+2xy 中,∵ d=x+(2x+1)y (x,y∈N)
我们依次取:
{y=1,x=1;{y=1,x=2;{y=1,x=3;……{y=1,x=i
{y=2,x=1;{y=2,x=2;{y=2,x=3;,……{y=2,x=i
……
{y=n,x=1,{y=n,x=2;{y=n,x=3;……,i}
把每次得到的d=Zh(x,y)的合数母数值,分别标在下面的直角坐标系xOy中。d落在对应的坐标交点d(x,y)上。定义这样的正整数格子点叫合数母数点,用d或d(x,y)来表示。这样我们就会得到图1所示的《素数母数合数母数在自然数中的分布图》也即是勾股数网络图。

图1
3 素数母数合数母数分布图(勾股数网络图)的特点
图1告诉我们:
(1)在x或y轴上的0和正整数点就是我们熟悉的自然数也就是我们现在介绍的母数!可见母数是披着自然数的外衣在显示自己的存在。或说自然数既有正整数的性质,同时包容有母数的性质。
在母数论层面,我们把X或Y轴叫作母数轴,母数披着自然数的外衣继承了自然数的正整数性自然数的母数性。并使它们生来就有从骨子里纠缠在一起,同时和而不同地包容一体和谐相处④。例如在X轴上,任意取出一个数4。首先我们可以认定正整数4是一个偶数,可作序数也可作为基数,是它正整数性的体现;同时,4也是一个合数母数,是奇数9的或说是子数9的母数,而且是一个合数母数。这是它母数性的体现…自然数的正整数性或自然数的母数性,它们会在具体应用中自然地一一区分开来。
(2)可以看到,根据 Zh(x,y)=x+y+2xy 或 d=x+(2x+1)y(x,y∈N)取的合数母数点,只要x,y取得足够多,≤一个充分大数的合数母数或说表示合数母数的点,无一例外地落在Oxy平面Ⅰ象限内部(有兴趣的读者不妨用反证法证明一下)。
就是说,合数母数d组成的集合D,落在xOy象限内部。同时要注意到,这些合数母数点完全包含在两个边界x,y轴上。无容置疑,这些合数母数确定的是自然数的一部分。例如图I中X轴上圈出的数…
(3)大家都已熟悉等差数列的通项公式是:
an=a1+(n1)d′或 an=(a1d′)+nd′(这里 d′是公差)
在图1中,我们可以规定 y=0,1,2,3,,i…,依次作为第0组,第1组,第2组,第3组,…第i组等差数列的序数。在图中i=a1d′,这样x成了对应等差数列的项数n或者说是公差d′的个数。
我们会看到合数母数完全包含在:
序数:x=0,1,2,3,4,…,ii=a1d′
公差:d′=1,3,5,7,9,…,2i+1
首项:a1=1,4,7,10,…,3i+1 或 A1=4,12,24,…,2n2+2n
末项:an≤N的i组等差数列内。(若充分大的正整数N已知)
(4)需要重点指出的是所有等差数列的序数即首项i,公差2i+1,和第一项3i+1或中数2i2+2i都是相互一一对应的关系,反过来也一样。例如:i=3是第3组等差数列,第一项a1=3i+1=10,公差d′=2i+1=7…等等。
(5)在函数Zh(x,y)=x+y+2xy(x,y∈N)中,x,y互换位置函数值不变,是对称函数。反映在图1中,合数母数d关于x=y对称。在应用中,用第一项依次为4,7,10…,3i+1,第一项还是用4,12,24,…,2i2+2i的等差数列求解合数母数的个数其结果是一样的。只不过用前者,把由于对称而重复的合数母数,包含在i组等差数列内,用后者已把重复对称的合数母数预先筛去罢了。
(6)我们可以把落在x=y上的合数母数A定义作“中数”。当x=y=n时,中数An=2n(n+1),它的数学定义是一个奇数(即子数)的母数n和其继数乘积的2倍叫做该奇数母数n的“中数”。如2n(n+1)是奇数(也叫子数)2n+1母数n的“中数”。简言之,每一个子数必定对应一个母数;每一个母数必定对应一个中数。前面也说过它们都是相互一一对应的关系。
显然,在 x=y=n 时,当取 n=0,1,2,3 ,4,…n 时,对应的中数分别是:
0,4,12 ,24,40…2n(n+1)….这个合数母数列我们把它叫作中数列需要指出的是,0虽也是母数,也是中数,但不是合数母数,后面的论文进一步论述。在图1中,为了醒目,把除了0以外的中数用粗黑体字标出,并红斜线贯穿。
通过对称性,我们可以把图1中,红色对角线和Y轴相夹的与另一侧和X轴相互对称的合数母数全部筛去(图中用=号划去的数)…
4 合数母数分布图(勾股数网络图)的应用
4.1 直观地判定素数和奇合数
(1)在母数论中,把图1的横坐标X轴称作母数轴。母数轴是由任意奇数2n+1的母数 n组成的。我们可以任意找一个数n,如果n在合数母数分布图1的象限以内,2n+1就是奇合数。如果n不在分布图内,2n+1就是素数。例如,15的母数是7,7显然在合数母数分布图中是合数母数,∴15就是合数。11的母数是5,5不在合数母数分布图中是素数母数,∴11就是素数…显然,我们是先把15,11视作正整数而且是一个奇数,然后根据定义找到它们的母数7和5,进而在分布图中进行比较…同时直观地显示出了:在母数轴中,自然数的正整数性和自然数的母数性交融一体包容一身的二象性质。
在图1中,还可以把母数轴上的母数和象限内的母数比较着看。例如,4,7,17它们同时在母数轴上和象限内都存在,∴它们是合数母数,由定义它们对应的子数或说奇数9,15,35 自然都是奇合数。而 1,2,3,…8,9…14…只在母数轴上存在,∴都是素数母数,它们对应的数 3,5,7,…17,19,…29…自然是素数…
(2)图1中取x=y右上方的合数母数点(含x=y上的点),即x=y和母数轴相夹的合数母数点(不含母数轴上的点)。如果,所取的合数母数是唯一的,即是所取图中没有重复出现的母数。那么,这样的合数母数的坐标点,就是素数母数 p′。
例如,4(1,1),7(1,2),17(2,3),…,d(x,y)等。∵ 对应的x,y的坐标点分别都是素数母数p′,∴2p'+1是素数。如上2×1+1=3;2×2+1=5;2×3+1=7 ,…对应都是素数。
4.2 分解奇合数
在合数母数分布图中任找一个合数母数d(x,y),横坐标x,纵坐标y的值,就是这个合数母数所对应的奇合数的两个奇数因子的母数。
例如,已知奇数15的母数是7,又知7的坐标7(1,2);∴15= (2×1+1)(2×2+1)=3×5 ;又如,有奇数 45,知母数 22(1,7),∴45=3×15;同时有22(2,4),∴45=5×9,其中 7(1,2);4(1,1)∴对应有 15=3×5;9=3×3;∴45=3×3×5…等等。
4.3 求勾股数
前面说过用分布图求勾股数时,把分布图图1叫作勾股数网络图。因为它像网络一样,能网尽我们想要的勾股数。正如图1中,用红线把落在图中所示的直角三角形三个顶点的合数母数点连接起来。这样在xOy平面内的每一个合数母数点d(不含X,Y轴),都在不同的直角三角形的三个顶点上。直角三角形两个锐角顶点的合数母数分别是中数A1和A2。
因为勾股数出自平面几何的直角三角形,在图1中我们示用的R t△A1-d-A2来演示,如何使用论文1的勾股基本定理,求出我们需要的勾股数。
4.3.1 求基本勾股数
最便捷的是,从母数轴X上取任意母数,每一个母数都可以确定一个子数。以这个子数为勾,就可以求出由它的母数确定的基本勾股数。
步骤如下:例如第一步,我们取带圈的④⑦两个合数母数,它们对应的子数必然是奇合数9和15。分别以9和15为勾;第二步,顺着以④⑦为首项为序数的两个直列等差数列,在X=Y轴即中数轴上找到4和7的中数40和112;第三步,根据基本勾股定理的公式Z1弦分别为股+1即41和113。这就很直接直截了当地写出所求的基本勾股数分别为9,40,41和15,112,113。
我们也可以在图标的R t△4-7-12中:∵74=3,以3为勾;3的母数为1,找到1的中数是4,以4为股;4+1=5,以5为弦;∴3,4,5(中数+1),为所求勾股数;
同理:在R t△12-17-24 中:∵1712=5,∴5 的母数为 2,找到2的中数12为股,弦=中数+1=13,∴5,12,13为所求勾股数;
同理:在R t△A1-d-A2中,我们只要依中数从小到大的顺序,取和中数差一位的合数母数d画出R t△,∵dA1=d'(公差),这个公差对应的公式正是2n+1,∵d'=2n+1,∴我们有论文1的勾股基本定理作保证:任意一个大于1的奇数(勾)的平方与该奇数母数对应的“中数”(股)的平方和,等于此“中数”后继数的平方。表示作:
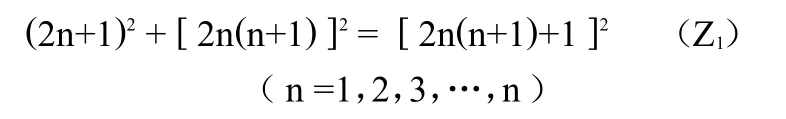
来保证我们这样做的正确性。这样,在网络图中可以简单准确地求出基本勾股数。
4.3.2 求基本勾股数的倍数勾股数
求这样的勾股数,一般只要原勾股数各项,同时乘以一个整数倍数就可以了。但这里说的是从图1的网络图中,也可以求出它们:
例如,在Rt△4-10-24 中:∵104=6 ,6=2(倍数)×3(公差d′),3 的母数是 1,1 的中数是 4,∴ 由 3 为勾有 3,4,5.
∴3×2,4×2,(4+1)×2 即 6,8,10 为所求勾股数。
同理在R t△12-27-60 中:∵27 12=15 ,15=5×3 ∴5×3,12×3,(12+1)×3
又有 15=3×5 ∴4×5,5×5,(5+1)×3
即 15,36,39 和 15,20,25 都为所求勾股数…可见可以网尽倍数勾股数。
4.3.3 求网络勾股数
用网络图除了能求出前两种勾股数外,还能求出网络勾股数。在网络图中取x=y右上方的任一个合数母数d,以合数母数d确定的奇合数2d+1为勾,以三角形两顶点的两个中数之差A2A1为股,那么,两个中数之和的继数即A1+A2+1一定是弦。利用这种方法在网络图中可以网尽第三种勾股数。
例如在Rt△4-7-12 中:勾为 2×7+1=15,股为 124=8,弦为4+12+1=17
∴15,8,17为所求网络勾股数。
又如在R t△12-22-40 中:勾为 2×22+1=45,股为40 12=28,弦为 12+40+1=53
∴45,28,53为所求网络勾股数。
在R t△4-22-112 中:勾为 2×22+1=45,股为 1124=108,弦为4+112+1=117
∴45,108,117为所求的倍数勾股数,各项除以9,得一组基本勾股数 5,12,13…
网络图所演示的求网络勾股数的正确性,也是由论文1勾股基本定理系2。取任意两组不相等的基本勾股数,a1,b1,c1和 a2,b2,c2可组成新的勾股数:a1a2,│b2b1│,b2+c1来保证的⑤,
∵c2=b2+1,a1a2=2n+1。∴b2+c1=b1+b2+1
实际上,用网络图求勾股数的原理是:运用合数母数分布图,把论文1的勾股基本定理重新更直观的演示了一遍…
5 结束语
最后,需要指出的是,我们依赖的合数母数函数Zh(x,y)=x+y+2xy,它是一个关于x、y的二次函数。当且仅当x,y在正整数范围内取值时,才有合数母数方程d=x+y+2xy。当x,y的定义域扩展到实数时,二次函数的几何意义是空间曲面。我们利用这一点,会演绎出:母数方程n=x+y+2xy无正整数解时n就是素数母数。在网络图I中我们已经清楚地看到了这一点。
所以,合数母数d应该是空间曲面上的正整数点,在xOy平面上的投影。反映了合数母数d和变量x,y在空间曲面的结构逻辑中的纯数量关系。
而这些空间曲面结构逻辑和数量关系的抽象,正是同时包含加法和乘法的最优也是最简化的模式2n+1分解时的产物!它们是形成母数论抑或说网络数论的根据。至于网络图I中用红线标出的Rt△只是用来演示如何用母数理论求勾股数的。所以,那些图标边长与图上R t△实际边长是相悖的,因为它们不在一个平面内。但它却能从母数的层面准确地把握住了平面几何中的勾股数。
在图I内,合数母数d(x,y)至少有两个正整数解x和y,这恰恰同时是合数母数 d对应构造的奇合数2d+1所分解的至少两个奇因数的母数!在整个分解过程中,我们既看到了也感觉到了自然数的正整数性又同时看到了感觉到了自然数的母数性。随着母数的推广应用,我们会逐步体会到母数的包容性,母数的纠缠性,母数的创造性…母数的性质必然折射出更广义的哲学思想。例如,包容就应该升华为广泛的哲学概念,这是后话。
为了区别以往用初等数论和平面几何的方法求解合数、素数、勾股数的方法,我们能否把用母数理论求解素数合数及勾股数的方法叫作母数论或网络数论。
另一方面,自然用这种方法求出的勾股数叫网络勾股数。狭义上说,网络勾股数是特指奇合数为勾,勾股弦互质,弦—股>1的那些勾股数。
符号说明:N为不含0的自然数也即正整数集n∈N;P为奇素数奇素数集 p∈N;p′为素数母数元素,E为素数母数集p′∈E;奇素数 P=2p′+1;d为合数母数元素,D为合数母数集 d∈D;合数(奇合数)M=2d+1。
注释
①⑤论文1系参考文献[1]所指的论文。
②网络勾股数,中数,中数列等概念见参考文献[1]的论文。
③论文2系参考文献[2]所指的论文。
④关于自然数的正整数性母数性,以及下面提到的母数蕴藏的哲学思考,在论文4《我对自然数的第三次认识》中将深入阐述。母数的纠缠性包容性等概念见参考文献[2]所的论文。

