广义Petersen图P(n,1)和P(n,2)的意大利控制数

高 红，黄佳欢，尹亚男，杨元生

（1. 大连海事大学理学院，辽宁大连116026；2. 大连理工大学计算机科学与技术学院，辽宁大连116024）

G=（V，E）表示一个图，顶点集合为V，边的集合 为 E。 顶 点 v 的 开 邻 域 为 N(v)={u|(u，v)∈E(G) }，闭邻域为N [v]=N(v)∪{v}。顶点v 的度是N（v）中包含的顶点的个数，即deg(v)=|N(v)|。图G的最大度和最小度分别记作Δ(G)和δ(G)。若对于任意的v ∈V，都有deg(v)=r，则图G称为r‒正则图。

在图G=（V，E）中，若D ⊆V(G)且N [D]=V(G)，则称D为G的一个控制集。控制集包含元素个数的最小值称为图G的控制数，记为γ(G)。图的控制有很多种类型，其中意大利控制［1］是一种新兴的控制类型，又称为罗马｛2｝‒控制［2］或弱｛2｝‒控制［3］。设f：V →{0，1，2}为图G上的函数，如果所有满足f(v)=0 的顶点v 在其邻域中至少有一个被赋值为2的顶点或者至少有两个被赋值为1的顶点，那么函数f 称为图G 的意大利控制函数。意大利控制函数的权重等于图G 中所有顶点的函数值之和，权重的最小值为图G的意大利控制数，记为γI(G)。若f 为图G 的意大利控制函数并且w( f )=γI(G)，则f 称为γI‒function。若图G 满足2γ(G)=γI(G)，则称图G为意大利图。关于意大利控制的研究可以参考文献［4-10］。

本文研究了广义Petersen 图P（n，1）和P（n，2）意大利控制数。通过构造可递推的意大利控制函数计算出意大利控制数的上界。利用袋装法和控制代价函数法分别证明出P（n，1）和P（n，2）意大利控制数的下界。最终确定了P（n，1）和P（n，2）意大利控制数的精确值。

1 P(n,1)的意大利控制数

1.1 P（n，1）意大利控制数的上界

广义Petersen 图P（n，k）是3 正则图，有2n 个顶点。图1a和1b显示的是P（6，1）和P（6，2）。为了便于表示Petersen 图的意大利控制函数，本文将P（n，k）表示为剪开的形式，图1c和1d显示的是P（6，1）和P（6，2）的剪开图。

设G=P（n，k），f 为图G 上的意大利控制函数，则有下面的形式：

1.2 P（n，1）意大利控制数的下界

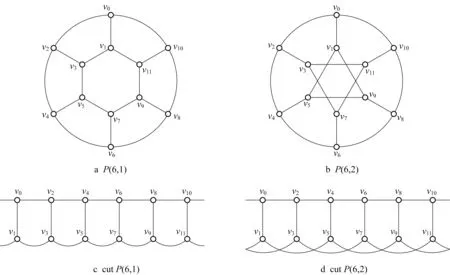
图1 Petersen 图P（6，1）和P（6，2）Fig.1 Petersen graph P(6,1)and P(6,2)

2 P(n,2)的意大利控制数

2.1 P（n，2）意大利控制数的上界

2.2 P（n，2）意大利控制数的下界

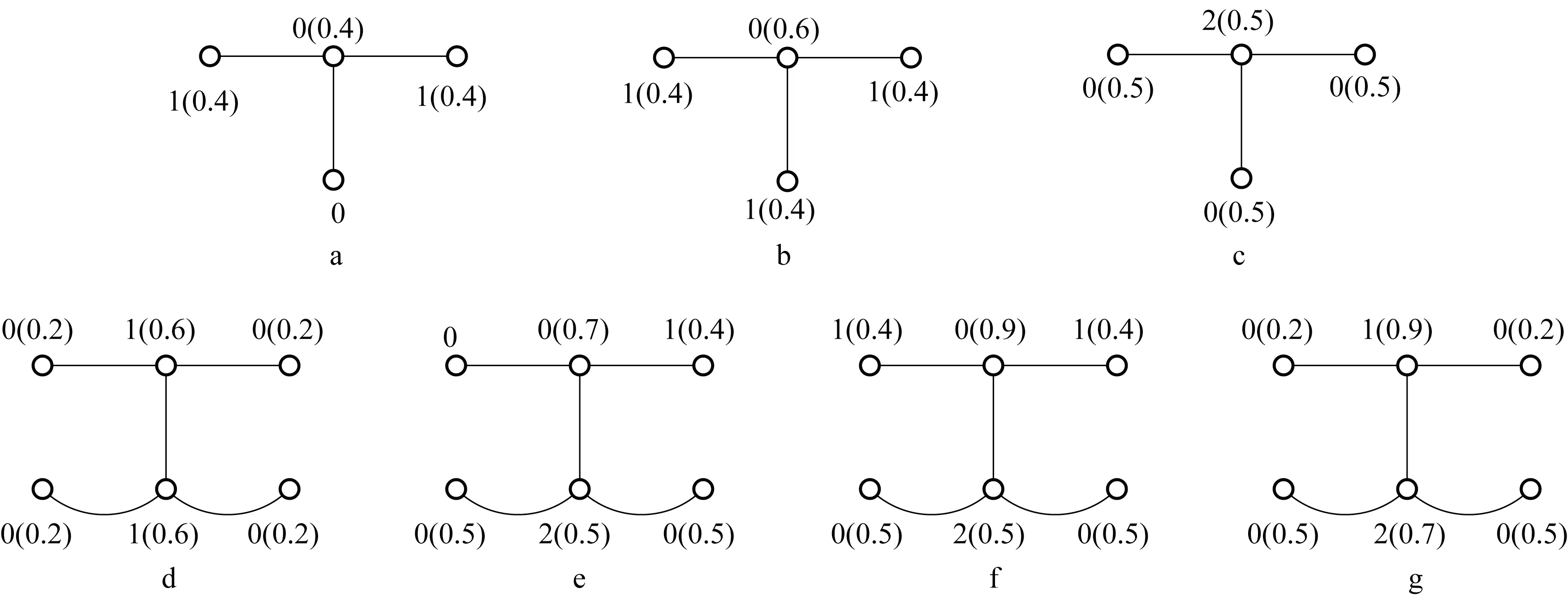
图2 命题2～8的示意图Fig.2 Sketches for propositions 2 to 8

|N(v5)∩V2|=1。 由 命 题6，rf(v)≥0.6＞0.4，矛盾。

图3 给出了情形（6）中意大利控制函数的示意图，图中黑色实心点表示f (v)=0的顶点，空心圆圈表示f (v)=1的顶点，较大的空心圆圈表示f (v)=2的顶点。

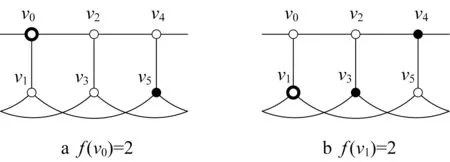
图3 情形（6）中的意大利控制函数f的示意图Fig.3 Italian domination function f in Case(6)

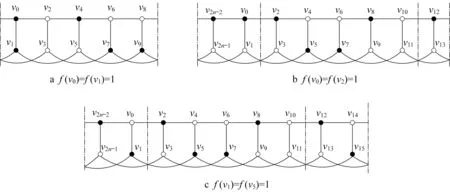
图4 情形（7）中的意大利控制函数f的示意图Fig.4 Italian domination function f in Case(7)

图5 给出了情形（8）中意大利控制函数的示意图。

情形（9）存在vi满足f(vi)=1且i≡0(mod 2)。

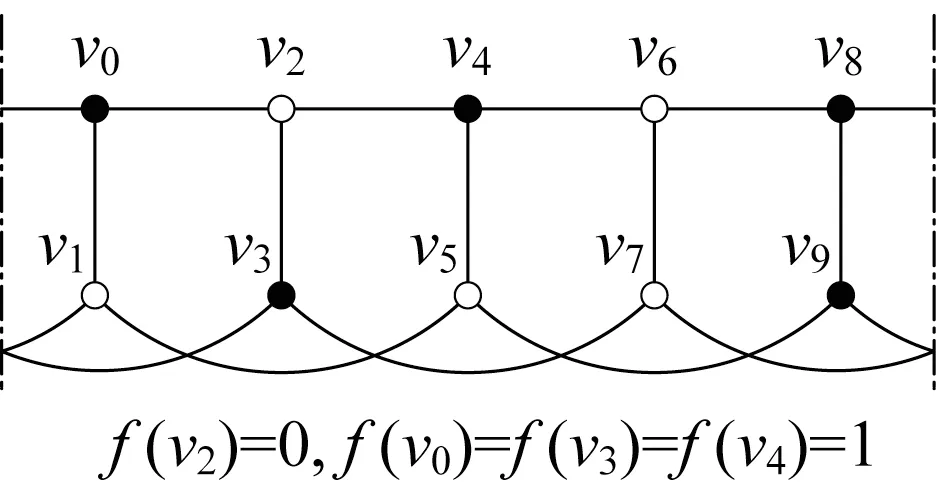
图5 情形（8）中的意大利控制函数f的示意图Fig.5 Italian domination function f in Case(8)

2.3 P（n，2）意大利控制数与2-彩虹控制数和经典控制数的关系

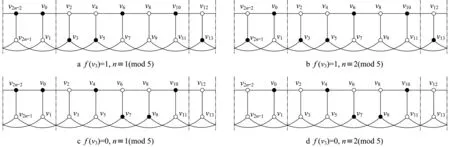
图6 情形（9）中的意大利控制函数f的示意图Fig.6 Italian domination function f in Case(9)

3 结论

作者贡献说明：

高 红：提出证明方法，算法总体设计，论文定稿。

黄佳欢：论文写作，画图，程序编写。

尹亚男：论文初稿的写作，程序调试。

杨元生：方法指导和程序设计指导。