一种加权整体最小二乘估计的高效算法

王建民，倪福泽，赵建军

（1. 太原理工大学矿业工程学院，山西太原030024；2. 成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川成都610059；3. 中煤（西安）航测遥感研究院有限公司，陕西西安710100）

高斯‒马尔可夫模型在许多工程实践中得到成功应用，通常认为模型中的设计矩阵是无误差的。然而，在许多情景下，设计矩阵中的元素并不能保证是常数，其本身也是含有随机误差的观测值，设计矩阵和观测向量中含有随机误差的模型通常被定义为变量误差模型（errors-in-variables，EIV）［1-2］。

最初，因为求解EIV模型参数的方法不成熟，通常忽略设计矩阵中的随机误差，而采用加权最小二乘法（weighted least-squares，WLS）近似估计EIV参数，这种方法是不严密的。1980 年，Golub 等［3］提出采用整体最小二乘法（total least-squares，TLS）估计EIV模型的未知参数。当设计矩阵和观测向量均含有随机误差时，TLS 就是最小二乘（least-squares，LS）的扩展且更具一般性［4］。TLS 将设计矩阵中的所有元素按等权对待，但实际上设计矩阵中的元素并非都含有随机误差，且精度也不尽相同，因此TLS被进一步扩展为加权整体最小二乘法（weightedTLS，WTLS），WTLS 分别给观测向量和设计矩阵附加了不同的权重，比TLS更具一般性。

一般来说，主要有两类方法实现TLS和WTLS的求解，一类方法是基于奇异值分解（singular value decomposition，SVD）的 直 接 解 算 方 法［4–8］，Akyilmaz［6］在SVD分解中给设计矩阵和观测向量赋予了相应的权矩阵，但引入的权阵并没有真正起到调配误差的作用，其本质上是对每个参数和观测值进行了缩放［9］。另一类常用的方法是基于拉格朗日辅助法构建极值函数分别对未知量进行求偏导数，许多文献据此提出了WTLS的迭代算法［2，5，8，10-12］，建立在统计框架下的这些迭代算法估计EIV模型参数是严密的［13］。因为WTLS 同时顾及了设计矩阵和观测向量的权重，在工程实践中应用迭代法估计EIV模型参数更为普遍。

从现有的研究成果来看，虽然国内外学者就EIV 模型提出了许多卓有成效的解算方法，但是与传统的WLS 相比，算法比较复杂，不具有操作上的优势［14］，而且大多数迭代算法仅考虑了参数估计精度和迭代收敛速率，当面临大数据集时计算效率有限。

为了提高WTLS 的效率，一些学者从不同侧面改进了WTLS 算法。Shen 等［10］提出基于Newton-Gauss 的非线性WLS 平差方法，Jazaeri 等［15］导出了基于WLS准则下的迭代算法，这些方法都明显提升了迭代收敛速率。但仅通过增强迭代收敛速率，计算效率提升有限。事实上，绝大多数EIV 模型的设计矩阵具有结构性特征，仅有部分元素是随机的，其通常的解法是构造特定的权矩阵，使系数矩阵中固定元素位置的改正数为零，但这样会导致部分矩阵维数增大，从而加大了矩阵的运算量，不利于计算效率的提高。为此，Xu 等［9］提出了partial EIV（PEIV）模型，并给出了相应的算法。PEIV模型一个显著的优点是未知数的总量明显减小，然而多次迭代收敛拖慢了其计算效率［9，16-17］。Zhao［17］应用拉格朗日辅助法对参量求导增强了PEIV 算法的效率，王乐洋等［16］应用间接平差的原理进行改进，使算法更加简洁、紧凑。这两种方法改进的结果是迭代快速收敛，效率明显提高，但不足之处是需要根据原设计矩阵的结构解析出一个固定矩阵和固定向量，而且在迭代过程仍需重构设计矩阵，不利于效率的提升。

WTLS在大地测量等众多科学研究和工程领域中得到应用［18-19］，WTLS算法基本成熟，渐成理论体系。算法之间的差异主要体现在计算效率和算法原理的复杂程度上。在大数据的背景下，计算效率是决定算法能有效应用的一个重要因素。例如应用WTLS处理点云数据，数据量会显著增加，算法性能就会显得尤为重要。

本文针对EIV模型设计矩阵呈现出的结构性特征，将设计矩阵分成随机和固定部分，仅给随机部分赋予权重，并且不涉及拉格朗日辅助法对参量求偏导，在WLS 平差约束准则下，推证了一种估计EIV模型参数的迭代算法，该算法能够显著降低矩阵的运算量，极大提升计算效率。

1 基于WLS 准则的WTLS 高效算法原理

1.1 EIV模型及WTLS算法

EIV模型的函数模型和随机模型通常表示为［8-9］

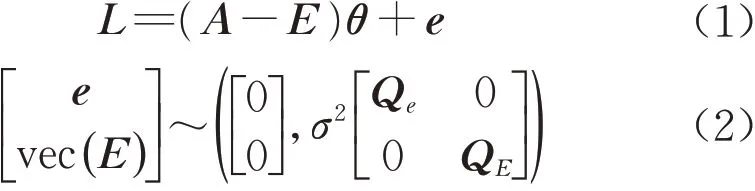
式（1）、（2）中：E为（n×t）阶设计矩阵A的随机误差；e为n维观测向量L的随机误差；（n×n）阶矩阵Qe和（nt×nt）阶矩阵QE分别为e 和vec（E）的协因数矩阵；vec（⋅）表示矩阵的拉直变换；θ为待估计的t个未知参数；σ2为单位权方差。

对于EIV 模型，可直接应用最小二乘准则eTQe-1e=min，其参数估值为［15］

仅对随机误差e 加以约束，难以估计E，一般的WTLS的平差准则为［10-11，15］

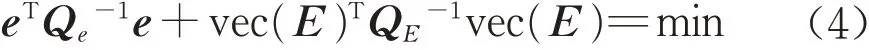
在式（4）的约束条件下，利用拉格朗日辅助法可以精确估计未知参数θ［8］，即

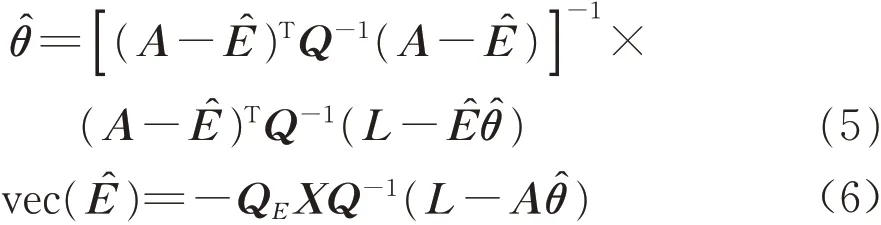
式（5）、（6）是WTLS 常用的迭代算式，一般的WTLS 方法在迭代过程中需要更新矩阵Ê，不利于算法效率的提升。接下来，根据设计矩阵A 呈现出的结构性特征，推导一种基于WLS准则的EIV模型参数估计高效算法。

1.2 顾及设计矩阵结构的WTLS算法

理论上EIV模型中的设计矩阵的元素均可包含随机误差，但在实际应用中，绝大多数EIV模型的设计矩阵都会存在部分固定列并且不含有随机误差［9，17，20］。对于含有固定列的设计矩阵，通常是构建一个特定的协因数矩阵QE，在迭代的过程中使得固定元素的改正数为零，但这样会导致QE的维数被固定列“扩大”，制约了计算效率。

设A中有t1列固定列和t2列随机列，将A中的固定列和随机列进行矩阵分块，对应的参数θ 也分成两部分，即

式（7）、（8）中：A1为由固定列组成的（n×t1）阶矩阵；A2为由随机列组成的（n×t2）阶矩阵；与A1和A2对应的参数分别为θ1和θ2。

根据式（7）和式（8），EIV 模型（式（1）和式（2））重新改写为

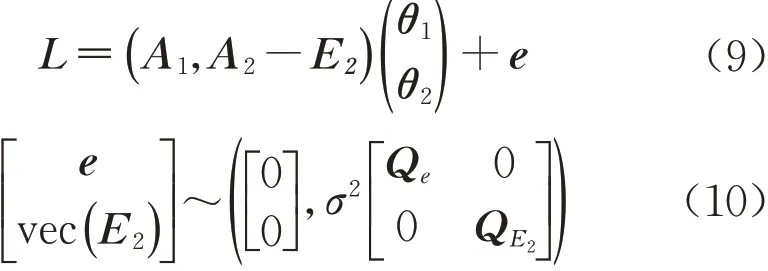
式（9）、（10）中：E2为A2的随机误差矩阵，其阶数为（n×t2）；QE2为vec（E2）的协因数矩阵，其阶数为（nt2×nt2）。

将式（9）改写为以下误差方程：

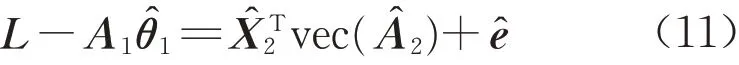
顾及式（11），vec(A2)表示为

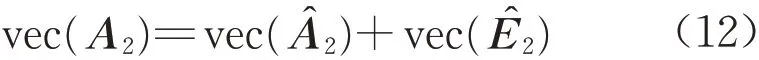
将式（11）和式（12）组合形成如下的非线性方程，即

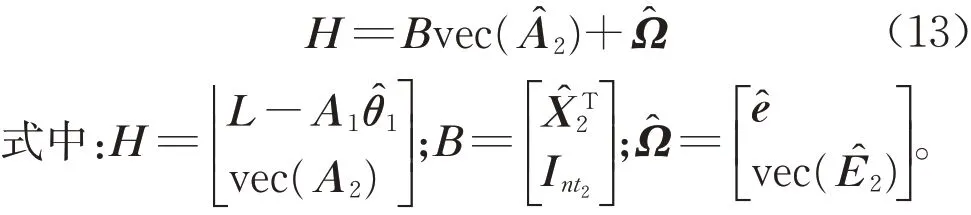
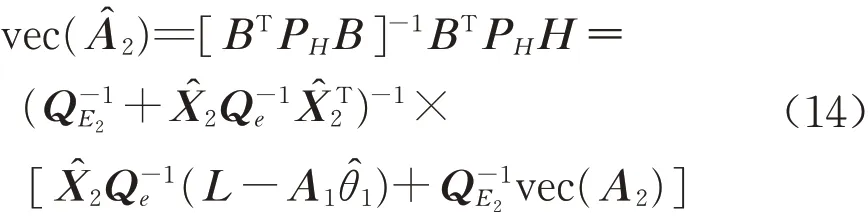
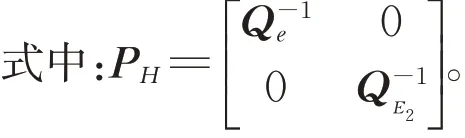
为进一步化简式（14），需利用式（15）的矩阵求逆引理［21］，即

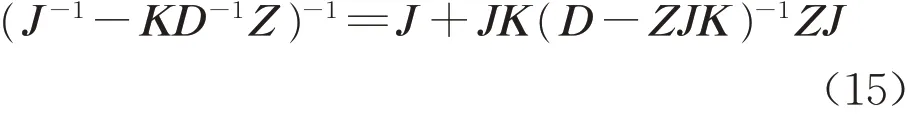
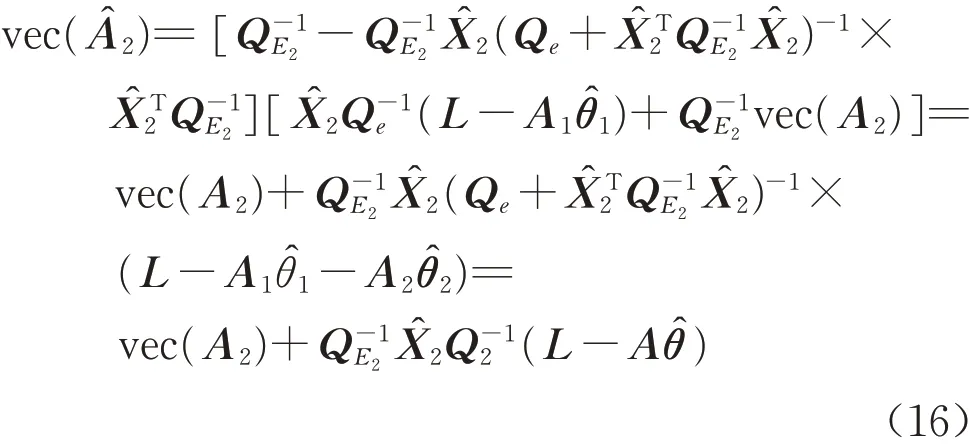
由式（16）可知，设计矩阵A2的随机误差的估值为

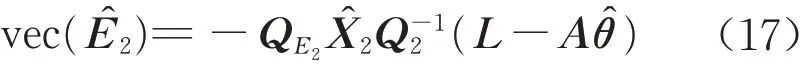
由式（7）可知，观测向量L的残差可表示为

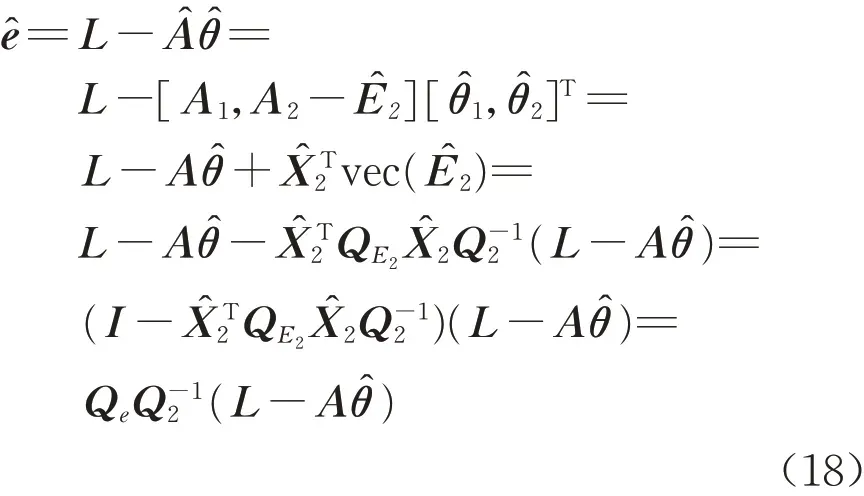
由式（18）可知

将式（19）代入式（3），得

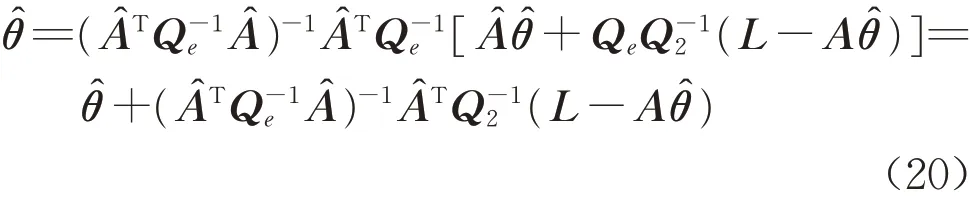
则

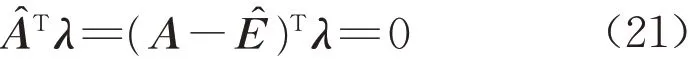
式中：λ=Q-21(L-Aθ̂)，λ为n×1的向量。由式（21）可知

根据A的矩阵分块（式（7）），式（22）可分解为两部分，即

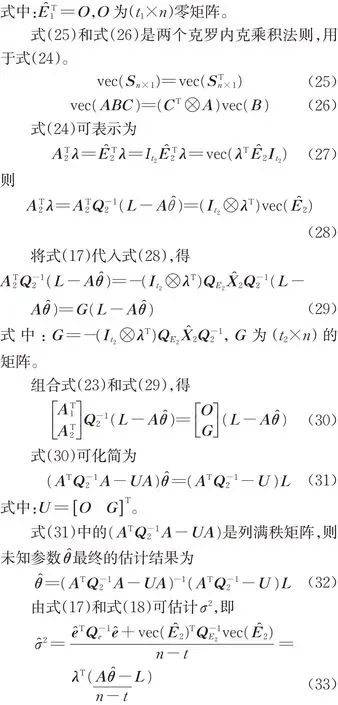
上述推导是基于WLS 最小二乘准则，并且式（32）在形式上与间接平差的法方程类似，但方程两侧都存在未知参数θ̂，仍需迭代计算。为了加以区别和简写，上述算法称为部分加权整体最小二乘法（partially weighted TLS，PWTLS），PWTLS 的算法流程步骤如下：

由上述算法可知，在迭代过程中，并不涉及对设计矩阵A拆分成A1和A2，仅需把随机列A2对应的参数θ2分解出来参与迭代。只要EIV模型的设计矩阵存在固定列，根据列与参数的对应关系，很容易将A组合成固定和随机部分。通常情况下，习惯上总是将EIV 模型的固定列排列在一起，而且绝大多数EIV 模型至少有一列是固定列，因而PWTLS 估计EIV参数具有普适性。另外，在实际应用中，设计矩阵的随机列可能会含有少量固定元素，例如三维七参数坐标转换模型中，有3列固定列组成A1，在随机列中有一个固定零元素，对于随机列中的个别固定元素赋予值为零的协因数后，仍可组成随机列A2。

从算法流程可以看出，PWTLS 算法不同于一般的WTLS 算法，在每次迭代的过程中并不需要估计随机误差E；通过给设计矩阵的随机列赋予权重，使得相关矩阵运算的时间复杂度由O（nt）降低到O（nt2），占用的内存空间由O（nt2）减小到O（nt22），例如原参数矩阵X̂的维数（nt × nt）降为X̂2（nt2×nt2），基于这两点，使PWTLS算法的效率显著提高。

2 算例与分析

为了验证PWTLS的性能，本文选择了7种具有代表性的WTLS算法［10-11，15-17，20，22］与本文算法进行对比分析，这7 种算法从不同角度对WTLS 进行效率增强，具体原理见参考文献，有的算法在相关文献中也与其他算法进行过对比研究。

2.1 真实算例

直线拟合简单而有效，经常用于证明WTLS 算法的有效性。设有直线方程为y=ax+b，其中x 和y 是直线的坐标分量，a 和b 是直线的斜率和截距。实验数据来自于文献［23］，见表1，其中（xi，yi）和（wxi，wyi）表示坐标和相应的权值。

根据直线方程和坐标点数量，设计矩阵A，参数向量θ及观测向量L具体形式为

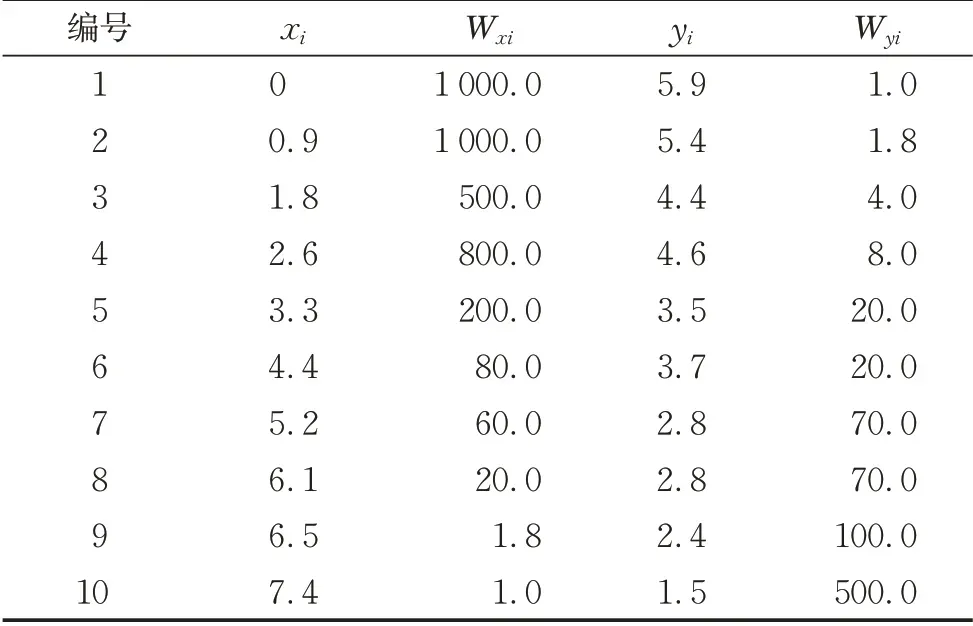
表1 坐标观测值和相应的权重Tab.1 Coordinate observations and weights

在式（35）中，设计矩阵A 可分成A1和A2两部分，即

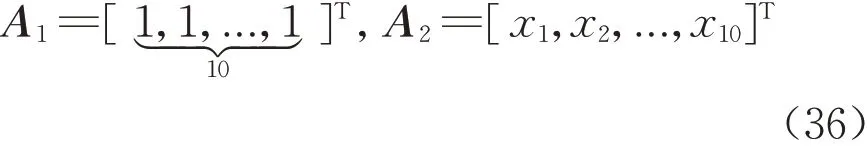
A2的协因数矩阵QE2的结构取自QE的一部分，即

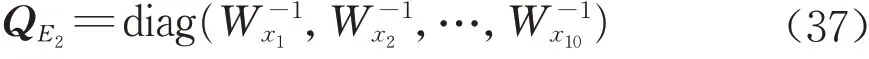
设迭代收敛阈值ε=10-10，分别应用8种算法估计参数和单位权中误差，实验结果见表2。从表2中可明显看出，8 种严密算法估计的参数相差在10-11量级且中误差相同，表明PWTLS能够获得和另外7种严密算法相同的解。文献［22］对PEIV 模型进行改进，其目的也是提升效率，从本例的结果来看，收敛速度高达454 次，其余算法的收敛速度都较快。文献［16］同样是对PEIV模型算法进行优化，取得了理想的效果。比较而言，文献［20］的算法收敛最快，收敛速度仅是影响计算效率一方面的因素。本例中直线拟合的设计矩阵结构简单而且仅有10个点，主要用于PWTLS参数估计精度的验证及收敛速度的初步分析，接下来通过大数据量应用仿真模拟实验来对比分析各个算法的效率。

表2 8种不同算法的参数和中误差的估计结果Tab.2 Estimated parameters and standard deviations obtained using eight algorithms

2.2 仿真算例

平面相似四参数转换模型是常用的坐标基准转换模型之一，通常由式（38）表示［24］

式中：ξ 和η 为平移参数；k为尺度参数；a为旋转角；下标S和T分别表示原坐标系和目标坐标系。

假设有d 个重合点用于求解转换参数，式（38）经过变换可由EIV 模型描述，设计矩阵A，参数θ 及观测向量L表示为

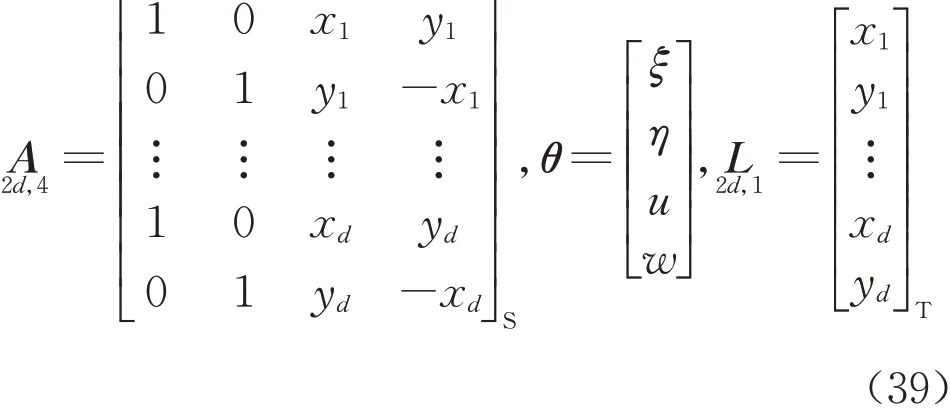
式中：u=k cos a；w=k sin a为辅助参数。

参数ξ 和η 对应的系数是1 和0 的常量，设计矩阵A 的第1 列和第2 列是固定列，组成A1；其他两列组成A2形成随机列，A1和A2表示为

对应于A1和A2，相应的参数可分成两部分，即

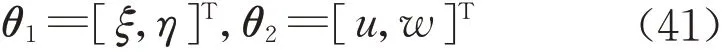
原坐标系中的坐标由随机函数产生d 个坐标点，目标坐标由给定的参数真值ξ=-27.366，η=-71.185，u=1.000 001 092 和w=6.400 15×10-7通过转换模型反算得到。原坐标和目标坐标中的随机误差由随机函数（式（42）、（43））随机生成，并将随机误差附加到相应的坐标分量中。

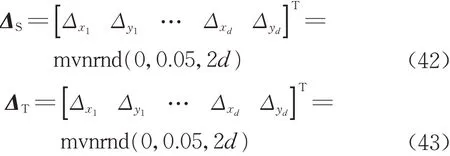
式中：ΔS和ΔT分别表示原始坐标和目标坐标中的真误差，mvnrnd（0，σ，2d）生成期望为0、标准差为σ=0.05 m、维数为2d×1的随机向量。

由随机误差和标准差定义观测量向量L的协因数阵QeT

根据设计矩阵A2的结构，vec（A2）的协因数阵QE2定义为

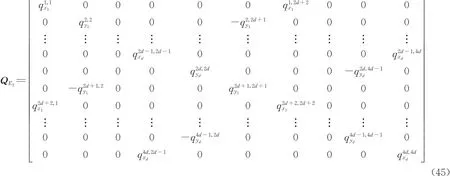
基于上述的模型和数据，随机模拟1 000 次实验，固定重合点数d=200，应用均方根误差（RMSE）来衡量参数估计的精度，参数ξ、η、u 和w 的RMSE由式（46）、（47）估计

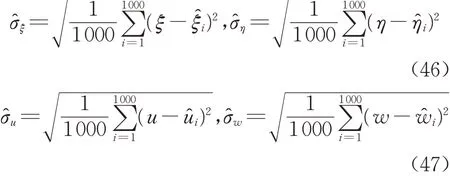
式（46）、（47）中：ξ̂i、η̂i、ûi和ŵi为经第i次模拟的对应参数的估计值。

在相同数据和计算平台的实验条件下（收敛阈值ε=10-10），分别应用7 种具有较高收敛速度的算法进行模拟，参数的RMSE的统计结果和1 000次模拟的累计耗时见表3，结果表明，严密算法中的RMSE差异为10×10-5mm，进一步证明了PWTLS与其他严密算法的参数估计精度相同。

从计算的总耗时可以看出，PWTLS 是所有严密算法中计算效率最高的，与其他算法计算效率相比，最少提高了161%，最多提高了近416%。其主要是因为PWTLS使用QE2代替了QE，维数由800×800 降到400×400；另外，在每次迭代过程中，PWTLS算法并不需要估计随机误差矩阵E。

为了突出PWTLS 计算效率的优越性，从另一个角度执行了10次模拟实验，要求重合点数据以间隔为100个点，逐渐从d=100增加到1 000。计算耗时统计结果如图1 所示，结果表明，PWTLS 的耗时曲线变化相对平缓，意味着随着数据量的增大，PWTLS 的优势越来越明显。

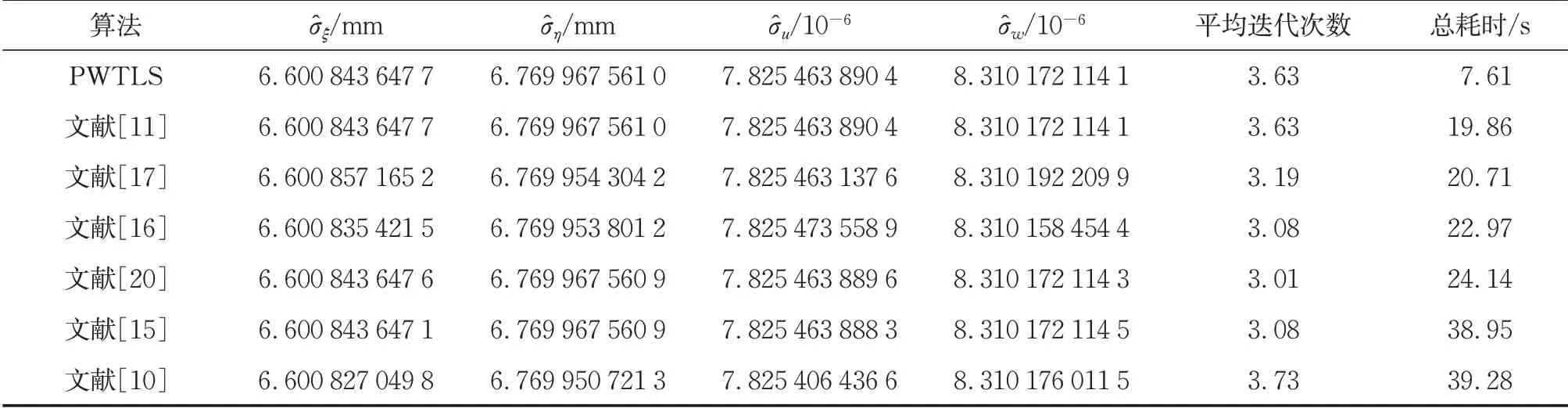
表3 1 000次模拟的RMSE和累计耗时Tab.3 Results of parameter estimation and details of the time consumed for different algorithms

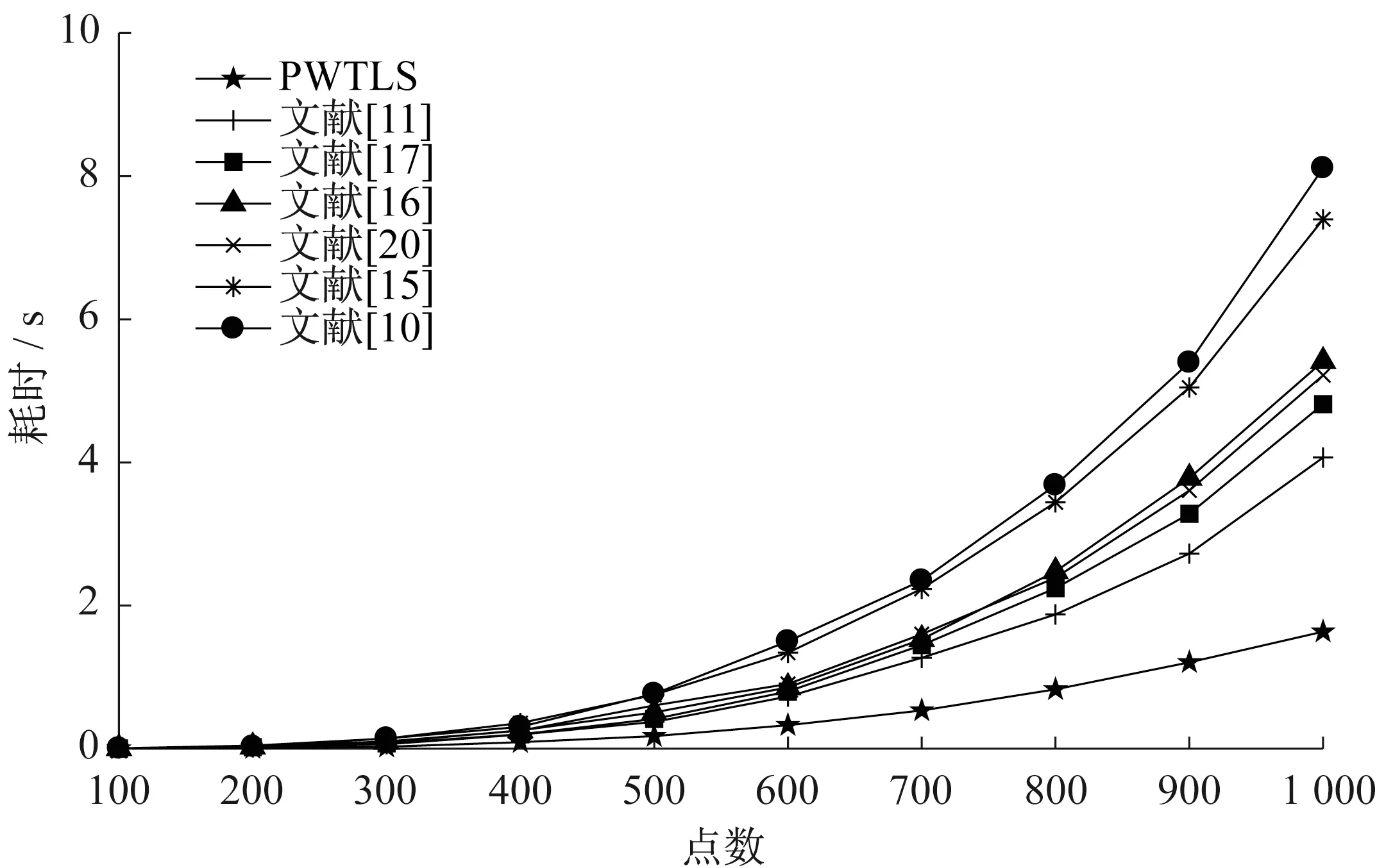
图1 7种算法的计算效率比较Fig.1 Computational efficiency of seven algorithms

3 结语

WTLS 已经在众多科学和工程技术中得到应用，当面临处理大数据集时，其计算效率有限，降低算法的复杂度和提高计算效率对WTLS 算法将显得越来越重要。

本文针对EIV模型的设计矩阵呈现出的结构性特征，提出了基于WLS 准则约束条件下的PWTLS算法，无需引入辅助量，迭代方程与经典的间接平差法方程类似，便于理解，易于实现，估计的参数是严密的。PWTLS 通过给设计矩阵中的随机列赋予权重，使得设计矩阵的协因数阵维数降低，从而在迭代过程中缩减了所有参与运算矩阵的维数，极大地减少了计算量，促进了效率的提升；另外，PWTLS 算法避免了重复估计设计矩阵随机列的误差，这两方面的因素使矩阵的运算量降低，从而显著提升了计算效率。最后，通过算例验证了所提出的PWTLS算法与同类算法参数估计精度相当，但计算效率显著提高。

作者贡献说明：

王建民：提出了论文中PWTLS算法原理，完成了论文的整体写作。

倪福泽：编写了计算程序，完成了论文中的实验计算和分析，绘制了图表。

赵建军：提供研究经费的资助，修改了中英文摘要。