基于数据驱动的城市地下快速路跟驰行为模型构建
张兰芳,朱佩玄,杨旻皓,王淑丽,史 进
(1. 同济大学道路与交通工程教育部重点实验室,上海201804;2. 上海市城市建设设计研究总院(集团)有限公司道路与桥梁设计研究院,
上海200125)
随着我国各大城市建设和城市交通的高速发展,地面交通发展已趋于饱和。为满足日益发展的交通需求,缓解地面与高架路的交通压力,城市地下快速路工程在各大城市逐渐兴起。地下快速路指利用地下空间、采用多层交通技术建设的全封闭的城市快速路。与地面道路相比,地下快速路具有有效利用城市空间、受外界环境影响小、不影响城市景观等优点。但是由于其行车环境与城市地面道路不同,因此在交通状况、驾驶行为特性等方面都与地面道路存在着较多差异。
车辆跟驰(car following,CF)行为是最基本的微观驾驶行为,描述了在限制超车的单行道上行驶车队中相邻两车之间的相互作用。在城市地下快速路中,各车道的车流量一般都较大,且在部分路段会限制车辆进行变道,因此在城市地下快速路中车辆跟驰行为更为普遍。对车辆跟驰行为进行建模可量化跟驰车辆间的纵向相互作用,揭示交通拥堵等交通现象的内在机理,在微观交通仿真、通行能力分析、自巡航控制、交通安全评价等领域都有着广泛的应用价值。
目前车辆跟驰行为的研究成果绝大多数是针对地面的城市道路和高速公路,对地下道路的研究非常有限,与之较接近的只有针对高速公路隧道的跟驰行为研究,如胡立伟等[1]对高原特长隧道驾驶人跟驰特性决策行为进行的研究,Yeung等[2]对新加坡地下快速路中的事故数据进行的研究,文中分析了地下道路环境对车辆跟驰行为的影响。此外,城市地下道路由于受路网、交通条件、建设条件等影响,还具有里程长、匝道出入口多、交通流量大、几何线形受限等特点,这些都使得城市地下快速路与地面快速路和一般公路隧道有较大的差别,因此宜针对城市地下快速路独特的交通运行环境对其车辆跟驰行为进行研究,构建城市地下快速路环境下的车辆跟驰模型。
车辆跟驰模型一般用以描述跟驰行为过程中车辆行驶状态的变化。对车辆跟驰模型进行研究,可以从微观角度量化跟驰车辆间的相互影响因素,包括车辆的速度、加速度、车间距等,进而得到交通流的宏观特性,如车流量、车流密度、平均车速。
自20世纪50年代以来,国内外学者对车辆跟驰行为模型进行了大量的研究,并取得了较为丰富的研究成果,其中主要有理论驱动类模型和数据驱动类模型两类。理论驱动类模型主要是以数学形式揭示跟驰状态中速度、加速度、车头时距等变量的关系。随着对理论驱动类模型研究的深入,在模型中又引入了驾驶员偏好、注意力等因素,提高模型复杂度和精度,如考虑最大意愿加、减速的Gipps模型[3]、引入期望车头时距的Helly模型[4]、考虑驾驶员感知及反应阈值的Wiedemann模型[5]以及元胞自动机模型等[6]。
当前理论驱动模型普遍存在的问题是很难在当前模型结构的基础上进一步有效提高模型的预测精度。理论驱动模型的模型结构是模型设计者提出的有关驾驶行为的理论假设。理论上,只有当理论驱动模型的模型结构可以全面描述不同交通状态下不同的驾驶行为时,才能表现出较高的预测精度,而这种条件往往很难满足。
数据驱动模型以车辆轨迹数据为建模基础,通过利用数据驱动方法对车辆轨迹数据进行统计分析,从而挖掘出车辆轨迹数据中与驾驶行为相关的内在规律并建立对应的数据拟合关系,实现对车辆跟驰行为的预测。根据所用数据驱动方法的不同,数据驱动模型一般分为以下4 类:模糊逻辑类模型[7]、人工神经网络类模型[8]、实例学习类模型[9]、支持向量回归模型[10]。由于数据驱动模型无需确定的模型结构即可建模,凭借其较强的数据学习能力,可有效地从车辆轨迹数据中挖掘出驾驶行为特性。当前的数据驱动类车辆跟驰模型的主要局限性是其对驾驶行为解释性的不足[11],如实例学习类模型使用车辆位置数据作为模型的输入、输出,缺少速度、加速度等能够描述驾驶行为的信息,造成对驾驶行为的解释性较差;支持向量回归类车辆跟驰模型的相关研究成果较少,目前研究中模型多数仅针对部分交通流状况,其有效性和适用范围都有一定的局限性,缺乏对宏观交通流的解释能力。
总结上述研究现状,可以发现目前对车辆跟驰模型的研究还存在以下两个方面的不足:
(1)针对地下快速路的车辆跟驰模型的相关研究较少。地下快速路环境会对微观驾驶行为产生影响,从而导致地下快速路与地面快速路有着不同的跟驰行为特性。现有的车辆跟驰模型无法很好地解释地下快速路环境中的交通现象。
(2)数据驱动模型以车辆轨迹数据为建模基础,可有效地从车辆轨迹数据中挖掘出驾驶行为特性。但目前的数据驱动模型多数仅针对部分交通流状况,其有效性和适用范围都有一定的局限性。
本文依托上海市北横通道东段线形及道路设施,采用高仿真多自由度模拟驾驶的手段获取车辆轨迹数据,结合合理的数据驱动类车辆跟驰模型并针对以上问题进行改进,从微观层面入手,对在地下快速路环境下的跟驰行为进行分析与建模。
1 数据采集与准备
目前,城市中地下道路的运用尚不普遍,即使是在国内很多大城市,大量地下道路仍处于建设当中。一方面,不同的地下道路间差异较大,出入点等许多方面的设置方式均有所不同,如外滩隧道,其线形条件很大程度上受到城市地下空间和多出入点规划的限制,不具有代表性。另一方面,在地下道路场景中,大部分轨迹数据采集方法并不适用,很难获取高精度的实车车辆轨迹数据。因此,本文采用模拟驾驶实验的方式进行车辆跟驰行为数据的采集,获得车辆的高精度轨迹数据。首先,相比于实车实验,驾驶模拟实验可以获得更精确的轨迹数据和各类参数。其次,可以设定不同的交通条件和道路条件,更加全面地反映驾驶员在不同状况下的行为特性。
1.1 模拟驾驶实验
1.1.1 实验设备
本次实验采用同济大学交通行为与协同虚拟现实实验系统的驾驶模拟器,如图1 所示。该驾驶模拟器的主要特征为:运动系统为8自由度运动系统;驾驶舱为封闭刚性结构,车辆置于球体中央,投影系统水平视角达250°;控制软件为SCANeR™Studio,该软件可以提供丰富的地形、场景和车辆模块进行模拟,并设有数据分析模块输出各类数据。使用该8自由度驾驶模拟器能够很好地还原真实的车辆运动系统,给驾驶员更真实的感受。此外,结合控制软件提供的丰富的道路环境和交通场景,使用该驾驶模拟器能够获取车辆运行过程中大规模高精度的运动数据,从而可以精准反映地下道路环境下每辆车的行为。
同济大学8自由度驾驶模拟器在视觉与动力感受方面都处于国际领先位置,与真实场景间的相似程度很高。根据张彦宁等[12]的研究,同济大学8 自由度驾驶模拟器在研究跟驰行驶状态下的跟驰距离、车头时距等方面都具有绝对有效性。根据刘阳[13]的研究,同济大学8 自由度驾驶模拟器在还原地下道路环境、设施等方面效果很好,在应用驾驶模拟器研究地下道路匝道时具有绝对有效性,在应用驾驶模拟器研究地下道路主线时具有相对有效性。之前研究者进行的研究,充分验证了该驾驶模拟器在研究地下道路与跟驰行驶状态下的有效性。因此,利用同济大学8 自由度驾驶模拟器可以还原地下道路真实的环境、设施和交通流条件,在进行地下道路场景下的跟驰行为研究时具有绝对有效性。
1.1.2 实验场景
为了保证驾驶模拟器场景与实际情况的一致性,北横通道东段三维虚拟场景建模主要包含以下步骤:首先,基于北横通道平、纵、横断面设计图以及隧道内装饰效果图等设计文件,将道路的各项信息进行数字化并导入SCANeR™Studio 形成三维模型,该模型包含驾驶模拟实验中的所有可视物体,效果逼真;其次,利用平、纵、横断面设计图建立行车逻辑层,并设置路面的坡度、材料以及行车道行车方向、限制车速、可通行车辆类型等;最后,对模型进行细节装饰渲染,对隧道侧壁、路面、标志牌、安全防撞设施等进行精细化贴图。

图1 驾驶模拟器Fig.1 Driving simulator
基于上述步骤,得到北横通道东段实验段模型全长6.9 km,设计速度60 km·h-1,车道宽度为每车道3.0 m,横断面布置为单管双层盾构形式,双向6车道。
在交通场景设计中,根据《城市道路工程设计规范》中快速路基本路段分级表和类似地下快速路的实际运行情况,对不同交通流场景进行分级,以期获得不同流量下的车辆跟驰数据,得到一个更通用的车辆跟驰模型,分级结果如下:
(1)自由流:平均车头间距125 m,平均速度75 km·h-1。
(2)稳定流:平均车头间距40 m,平均速度50 km·h-1。
(3)强制流:平均车头间距20 m,平均速度30 km·h-1。
1.1.3 实验人员选择
在进行驾驶模拟实验前,必须确定合适的样本量,即实验参与人员数量。假设所有驾驶员的驾驶行为服从正态分布,为了确保在α 置信度的前提下任意两次抽样总体的均值从认知角度没有差别,减少偶然误差,样本数应该大于20。考虑到部分驾驶人操作失误及数据筛选的因素,本次驾驶模拟实验通过不同渠道招募和选择测试驾驶员共54名,年龄跨度23~55 岁,驾龄从1~20 年不等,预实验表明,所有驾驶员均没有驾驶模拟器病,都可以顺利完成实验。
1.1.4 实验过程
首先,实验参与者需了解关于驾驶模拟器的使用说明以及完成实验前的准备工作,实验者需填写包含个人信息和驾驶经历等内容的基础信息调查表。之后,在正式实验前,实验参与者将在模拟器内驾驶指定的场景(城市地下道路)3~5 min,使其能够尽快地适应、熟悉驾驶模拟器的操作及环境。在正式实验中,每位驾驶员需按主线行驶过北横通道全程,全程约6.9 km,在3 种流量状态下分别完成1 组实验。驾驶员在整个实验过程中可自由选择车道行驶,以确保跟驰行为与换道行为的真实性。
北横通道上行、下行方向分为上、下两层,整个试验过程中54名驾驶员在上、下行方向均进行了自由流、稳定流、强制流3种不同流量状态下的驾驶模拟实验,通过对每位驾驶员行驶过程中的车辆位置、车辆运行状态、周围车辆数据进行记录,获得了大量的原始数据。
1.2 数据提取
驾驶模拟器数据采集系统以10 Hz 采集频率自动记录实验数据,主要记录的数据包括车辆位置、车辆运行状态以及周围车辆数据等。驾驶模拟器采集的原始数据字段如表1所示。
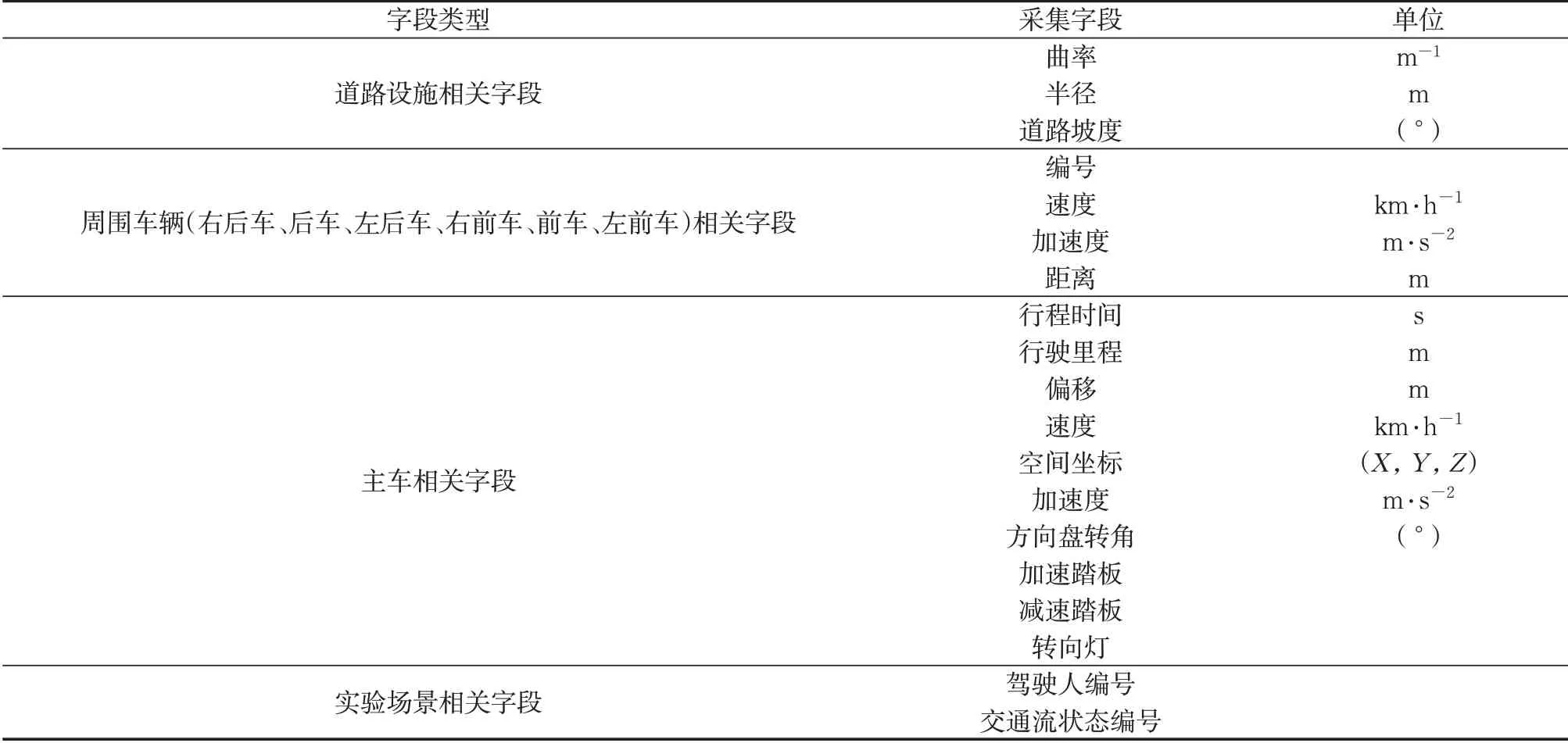
表1 原始数据字段Tab.1 Original data fields
首先,利用软件输出与跟驰行为相关的实验数据字段,即主车与前车相关动力学数据,如表2 所示。其次,为了满足参数标定与模型验证的需求,必须从数据集中提取出满足跟驰条件的相关数据,以保证包含充足、完整的信息。在进行跟驰片段挑选前,参考相关研究中的方法,主要对自车速度、与前车纵向距离、相对速度绝对值、跟驰片段时间长度、侧向距离绝对值等参数进行限制。如Leblanc 等[14]确定跟驰提取准则为自车速度大于40 km·h-1,相对速度绝对值小于2.0 m·s-1,片段长度为大于15 s;Chong等[15]确定跟驰片段提取准则为侧向距离绝对值小于1.9 m,自车速度大于20 km·h-1,纵向距离小于120 m,片段长度大于30 s。结合本实验中人工筛选出的跟驰片段数据特征进行提取阈值的修正,最终确定本文遵循以下原则对模拟驾驶实验得到的数据进行筛选,以挑选出合适的跟驰片段:

表2 跟驰行为相关数据字段Tab.2 Data fields related to car-following behavior
(1)前后车车速差绝对值小于2.5 m·s-1,相对速度的绝对值足够小以保证前后车辆处于稳定的跟驰状态。
(2)跟车间距小于120 m,用以排除自由流的交通流状态。
(3)跟车车速大于20 km·h-1,用以排除拥堵的交通流状态。
(4)跟车片段时长大于15 s,为了保证处于稳定的跟驰状态,跟驰片段不能过短。
经过筛选,得到车辆跟驰状态的轨迹数据共180个,总时长约92 min。
2 车辆跟驰模型的建立
2.1 模型选择
由于本文中获得的数据来源于模拟驾驶实验,可以获得行驶过程中每辆车的行为参数以及连续的车辆轨迹数据,数据样本丰富,因此更适合用数据驱动类模型对跟驰行为进行建模。此外,由于本文中跟驰数据按照不同交通流分为3 种流量状态,很难用单一的理论驱动模型来概括3种状态下的跟驰模型,因此使用数据驱动模型更为适合。
在数据驱动类模型中,支持向量回归(support vector regression,SVR)模型是一种基于统计学习理论的小样本机器学习算法[16]。支持向量回归遵循最小化结构风险原则而非最小化经验原则,其具有全局收敛和泛化能力强的特点,因此使其在理论上比人工神经网络更适用于车辆跟驰行为建模。利用支持向量回归进行车辆跟驰模型的建模,其结构如图2所示。图2中,输入变量通常为车头间距d(t)、前车速度vl(t)、后车速度vf(t),w、b为回归模型函数中的参数,输出变量一般为vf(t+∆t),即t+∆t 时刻的后车速度,具体的输入和输出变量根据建模思路的不同会有所差异。
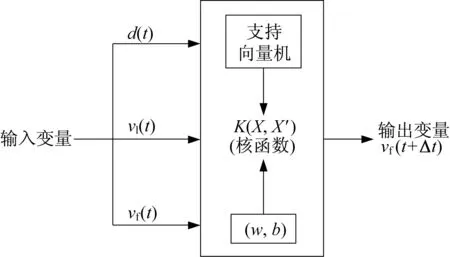
图2 基于SVR的车辆跟驰模型Fig.2 SVR-based car-following model
目前支持向量回归已经在图像处理、金融分析、能耗控制等领域有所应用,并取得了较丰富的研究成果,但是将其应用于车辆跟驰行为研究中的较少[17]。因为支持向量回归在解决复杂非线性问题上较传统方法有一定优势,理论上更适合对车辆跟驰行为进行建模,所以本文建立地下道路环境中的支持向量回归车辆跟驰(SVRCF)模型。
2.2 车辆跟驰模型变量相关性分析
在车辆跟驰模型中,常用的关键变量包括后车车速、相对速度和车间距等。本文初步选定SVRCF模型的输入为t 时刻的速度、相对速度和车间距,即x=(v(t),∆v(t),∆s(t));模型输出为t+∆t 时刻的速度,即y=v(t+∆t)。
通过分析速度、与前车速度差以及车头间距与加速度的相关性,从而获得与因变量v(t+∆t)相关的变量,以验证这些变量是否可以作为模型中的自变量。斯皮尔曼(Spearman)相关性检验不要求变量服从正态分布,且可以很好地减少异常值的影响,因此本文采用斯皮尔曼相关性系数来检验变量之间的相关性,检验结果如表3所示。

表3 变量相关性检验Tab.3 Variable correlation test
由表3可知,通过斯皮尔曼相关性检验,可以发现速度、速度差以及车头间距与加速度的显著性值均小于0.05,而且相关系数表明,3个变量均与加速度在0.01水平相关性显著。因此,可以将速度v(t)、速度差∆v(t)、车头间距∆s(t)作为车辆跟驰模型的自变量进行建模。
2.3 考虑驾驶行为约束的支持向量回归车辆跟驰模型
对于数据驱动模型而言,无法直接通过调整约束参数来实现对驾驶行为的约束,因此一般只能通过在模型中增加约束条件来规避不合理的驾驶行为。一般考虑可能出现的不合理驾驶行为包括过大的加速度、减速度,超出限速、逆向行驶等。考虑到支持向量回归方法的实质是在求解一个二次规划问题,故可将驾驶行为约束条件引入到该二次规划问题中,从而改进模型以避免不合理驾驶行为的发生。
主要考虑以下4种基本的驾驶行为约束条件:
(1)车辆的加速度不超过理论的最大加速度,a≤amax。
(2)车辆的加速度不小于理论的最大减速度,a≥bmax。
(3)车辆的速度不超过路段限速或自由流车速,v≤vmax。
(4)车辆的行驶方向保持向前,v≥0。
以上条件主要保证模型不会输出不符合现实情况的数据,对于车头间距,已经将其作为自变量输入模型,无法通过输出的速度变量对其进行约束。在现实中,车头间距可能会出现取值较小的情况,通过对加速度和速度等驾驶行为的全程约束,以确保车头间距符合实际情况。
假设观测样本由l 个独立的观测组成,T={(x1,y1),…,(xl,yl)},xi∈Rn,yi∈R,i=1,…,l,考虑在线性函数集合中构建回归模型,为
f(x)=w x+b w ∈Rn,b∈R (1)
将驾驶行为约束条件用线性不等式来表示,得到SVRCF模型要求解的最优化问题如下:

式中:ε >0 为ε‒不敏感损失函数的参数;C>0 为惩罚参数;ξi、ξi*≥0为松弛变量;xi为输入变量;yi为输出变量。引入拉格朗日乘子αi、α*i、δ1i、δ2i、δ3i、δ4i,构造式(2)的对偶问题,并引入核函数K(xi,x)得到
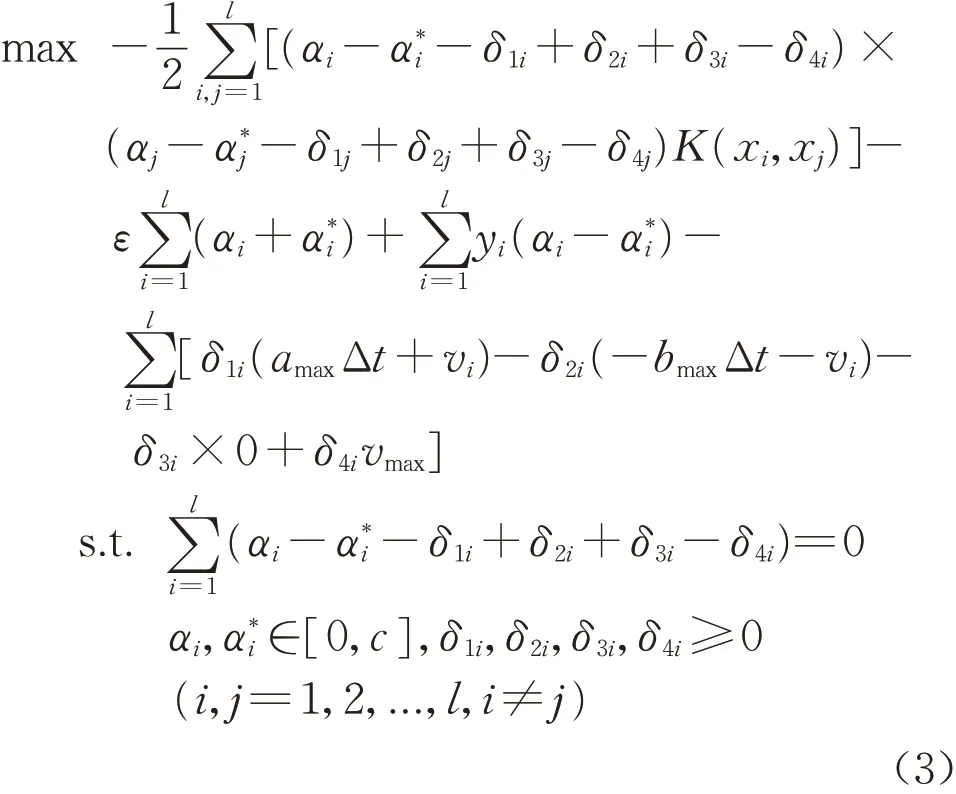
将模型输入、输出代入决策函数f (x),即得到SVRCF模型为
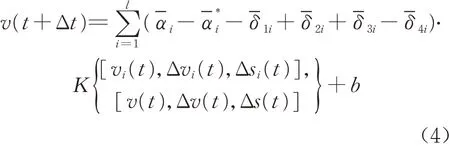
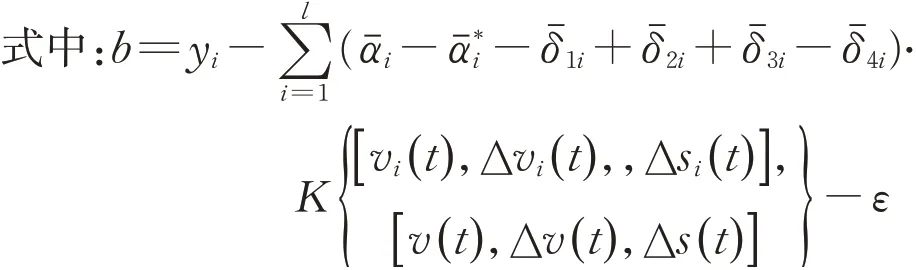
将SVRCF 模型中的核函数取为RBF 核函数,K(xi,x)=exp(-γ‖ xi-x‖2),此时 模 型 共有6 个待定参数,分别为惩罚参数C,不敏感损失函数的参数ε,RBF 核函数参数γ,最大加速度限制amax,最大减速度限制bmax,最大速度限制vmax。
3.1 驾驶行为约束条件的参数分析
首先需要确定归属于驾驶行为约束的参数amax、bmax、vmax。在驾驶模拟实验中已经获取了大量的跟驰数据,对这些数据分布特性进行分析即可获得上述这3个参数。
3.1.1 加速度分析
在进行驾驶模拟实验时,已经将场景交通流分为自由流、稳定流、强制流3 个等级。3 种流量状态下跟驰车辆加速度分布结果如图3所示。

图3 加速度分布直方图Fig.3 Histogram of acceleration distribution
在现有跟驰模型如Gipps 模型中,最大加、减速度的取值范围一般在[0.1,5.0]m⋅s-2之间。从图3可以看出,大部分加速度值都在[-2.5,2.5]m⋅s-2之间,大于2.5 的加速度值仅占0.49%,小于-2.5的加速度值仅占0.35%。选取amax=2.5 m⋅s-2,bmax=-2.5 m⋅s-2,可保证车辆处于合理的跟驰状态,不会产生过大的加速度和减速度。
3.1.2 速度分析
速度约束条件要求车速不出现大于限速或自由流车速的情况,分析驾驶模拟实验中自由流情况下的车速分布,如图4所示。

图4 自由流车速分布直方图Fig.4 Histogram of free-flow velocity distribution
从图4 可以看出,自由流车速大多分布在70 ~80 km·h-1的范围内,且在70 ~72 km·h-1的范围内分布较集中。自由流车速的平均值为75 km·h-1,而北横通道东段道路的实际限速为60 km·h-1,因此在建模过程中,给定约束条件为vmax为75 km·h-1,在保证车辆速度不过大的同时确保驾驶行为约束更符合实际情况。
3.2 评价方法
模型参数标定的过程就是寻找一组最优参数,使得模型的输出和实际值之间的误差最小。而寻找最优的参数则需要对应的评价方法,在回归模型中,通常使用的误差评价指标为平均绝对误差(MAE)和均方根误差(RMSE),其表达式如式(5)、(6)所示。

式(5)、(6)中:EMA为平均绝对误差;ERMS为均方根误差;l 为样本总数;yi为因变量实际值;ŷi为因变量预测值。
在标定模型参数时,学习预测函数的参数并在相同数据上进行测试会导致过拟合的情况,从而使得模型的表现能力不具有说服力。为了避免这种情况,本文采用k‒折交叉验证的方法,将样本点分成k组数量均等的子集,选取其中k-1组数据集作为训练集,余下的为测试集。经过总计为k次的迭代后,即可得到k组误差评价结果,其中误差最小的一组参数即可作为模型的最优参数。为降低计算复杂度,取k=10。具体算法如下:
(1)给定样本数据集合T,并根据k=10 将T 划分为k组数据。其中的k-1组车辆轨迹数据为训练集,剩下一组为测试集。训练集用于模型参数标定,测试集用于误差评价。
(2)将驾驶行为约束参数amax、bmax、vmax引入模型约束条件,并对模型有关支持向量回归方法的参数进行网格划分,得到M 组参数集合,记作{εm,Cm},m=1,…,M。
(3)对于第m 组参数集合{εm,Cm},给定训练集T,构造相应的SVR 模型,并在测试集Tk上利用RMSE 和MAE 对模型进行误差评价,评价结果记为em,k。
(4)重复步骤(3)以得到有关第m组参数集合的K 组误差评价结果,并对该结果求平均值
(5)重复步骤(3)和(4)以得到所有M 组参数集合的误差评价结果E1,E2,…,Em,其中最小误差min{E1,E2,…,Em}所对应的参数即为SVRCF模型的最优参数。
3.3 参数标定
基于上述的数据准备和评价方法,本文采取北横通道东段上行方向模拟驾驶实验跟驰片段的车辆轨迹数据作为训练数据,对考虑驾驶行为约束的支持向量回归模型SVRCF 进行参数标定。上述数据样本总时长为92 min,按照10 Hz 的频率采集数据,得到样本总数约为55 000 条,样本数量适用于支持向量回归建模。
如 式(4)所 示,SVRCF 模 型 的 输 出 为v(t+∆t),输入为v(t)、∆v(t)、∆s(t)。模型共有6个待定参数,其中根据交通流特性已确定取amax=2.5 m⋅s-2、bmax=-2.5 m⋅s-2、vmax=75 km⋅h-1。支持向量回归方法中的待定参数为C、ε、γ,本文采用网格搜索(grid search)算法来确定上述参数的最优取值。为降低参数寻优过程中的计算复杂度,将参数寻优范围依次设定为

对以上参数进行误差寻优,得到模型的最优参数组合为
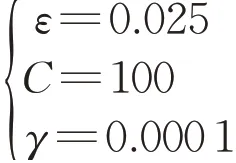
为更全面地展示误差评价结果,同时?使用了平均绝对误差(MAE)、均方误差(RMSE)、可释方差(EV),及R方值(R2)来评价模型的表现能力。其中MAE和RMSE用来表征模型的拟合误差,其值越小表明模型性能越好;EV 和R2则用来解释回归模型的方差得分,取值越接近于1 越说明自变量能解释因变量。具体的结果见表4。

表4 训练集误差结果Tab.4 Error results of training set
由表4可知,对于训练集来说,平均绝对误差与均方误差均小于1,处于可接受的范围内,可释方差与R方值很接近1,说明所选取的自变量能合理地解释因变量的变化。
为了更好地证明模型不具有过拟合的现象,同时验证模型在局部片段也有较好的适用性,需要对模型在标定数据集上的预测精度进行验证。本文选取北横通道下行方向中的某一片段中的车辆轨迹数据来进行验证。选取的验证片段长度为50 s,验证集样本量约为500。由于北横通道下行与上行线形及长度存在差异,可以视作不同的两条道路,但是又有相似的地下道路环境特点,因此可以使用下行数据来进行模型的验证,以证明该模型有一定的推广性。
对验证集的数据计算各个误差评价结果,如表5所示。从表5 可以看出,平均绝对误差与均方误差虽然比验证集的误差大,但是仍在可接受的范围内,预测精度较高。由此可见,本文建立的车辆跟驰模型在小样本和大样本情况下均具有较高的精度,即可以说明在局部片段和车队全局都有较好的预测精度稳定性。

表5 验证集误差结果Tab.5 Error results of validation set
为了证明本模型的有效性,使用数据驱动类模型中的反向传播神经网络(back-propagation neural network,BPNN)和传统的SVR 模型对训练集进行建模,得到误差结果如表6所示。表6与表4结果对比可以看出,相比于神经网络模型和传统SVR 模型,本文提出的考虑驾驶行为约束的SVR车辆跟驰模型各项误差指标都较小,因此可以说明本文提出的车辆跟驰模型在地下快速路场景下有更好的适用性。

表6 类似模型训练集误差结果Tab.6 Error results of training set of similar models
4 结论
本文在总结现有跟驰模型研究进展的基础上,针对地下快速路提出了一种引入驾驶行为约束条件的支持向量回归(SVR)车辆跟驰模型,并使用北横通道东段驾驶模拟实验数据进行了标定与验证。该模型改进了SVR 车辆跟驰模型中对实际驾驶行为模拟的不足,扩充了车辆跟驰模型在地下快速路各种交通流场景下的适用性,为地下快速路的仿真模拟和车辆运行风险研究提供了基础。
通过驾驶模拟实验获得的北横通道上行方向车辆轨迹数据对SVR车辆跟驰模型进行标定,得到的训练集均方误差为0.219、可释方差为0.975,表明模型的误差较小,且对变异性的解释也较好。此外,利用北横通道下行数据对模型进行验证,得到的均方误差为0.369,表明模型具有可移植性,对于其他地下快速路的车辆跟驰行为也同样适用。
在本文中,由于数据来源有限,未能将模型应用到更多的地下道路来对模型的可移植性进行进一步验证。此外,本文选择使用驾驶模拟实验的方法对模型进行标定与验证,可能会由于实验的限制不能精准地还原地下道路的环境。随着数据采集方法的进一步发展,利用更先进的方法获取高精度、实时的实际道路数据对模型进行标定改进,可以提出更适合地下道路跟驰行为的理论模型结构,从而得到更符合实际情况、性能更佳的模型。
张兰芳:建立系统架构,论文审阅与修改。
朱佩玄:建模方法设计,论文撰写。
杨旻皓:课题来源,实验设计指导。
王淑丽:实验数据分析。
史 进:实验场景设计。

