基于最优R-Vine Gaussian Copula模型的服役大跨桥梁主梁失效概率分析
刘逸平,肖青凯,,杨光红,刘月飞,3,樊学平,3
(1. 华南理工大学土木与交通学院 广东广州510641;2. 兰州大学土木工程与力学学院,甘肃兰州730000;3. 兰州大学西部灾害与环境力学教育部重点实验室,甘肃兰州730000)
由于输入随机源(车辆荷载、温度荷载、风荷载等)相同,桥梁健康监测(BHM)系统在各个控制监测点采集的数据具有一定的相关性,进而监测点失效模式之间也存在相关性。如何合理利用这些监测数据并考虑监测点失效相关性来分析大跨桥梁主梁可靠度,便成为BHM 领域亟需解决的关键科学问题,可以为在役桥梁的安全评价和养护维护决策提供理论依据和应用方法。
桥梁可靠性研究主要是利用抗力信息(容许应变等)和荷载效应信息(极值应变等),采用合适的可靠性计算方法,进行构件或体系的可靠性分析。现定义桥梁监测点的可靠度为构件可靠度,而考虑多个监测点相关或独立的桥梁主梁可靠度为体系可靠度[1]。
基于BHM 数据并考虑监测点失效相关性的大跨桥梁可靠性研究已取得一些成果:文献[2-4]基于BHM数据,初步假定2个监测点失效模式非线性相关,采用贝叶斯动态二维Gaussian copula 模型研究了长春伊通河桥主梁可靠性的动态预测方法;Liu等[5]基于BHM数据,假定多个监测点失效模式非线性相关,采用贝叶斯动态多维Gaussian copula 模型研究了天津富民桥主梁可靠性的动态预测方法;刘月飞等[1]基于BHM 数据,采用C/D‒vine Gaussian copula模型对天津富民桥主梁截面的可靠性进行了评估分析;樊学平等[6]基于BHM 数据,采用贝叶斯动态C/D vine Gaussian copula模型对天津富民桥主梁截面的可靠性进行了预测分析;Liu等[7]采用多变量copula模型进行了桥梁结构的系统可靠性评估分析。上述研究中的pair‒copula 均为pair‒Gaussian‒copula函数,进一步验证了Gaussian copula函数在桥梁可靠性分析中的合理性和适用性。
由上述研究可知,基于监测数据并考虑监测点相关性的桥梁可靠性研究主要通过引入copula函数进行,但随着维度的增加,模型参数估计变得更为困难,缺乏灵活性和通用性,因而在高维相依性建模方法存在局限性。Vine Gaussian copula理论的出现解决了这个问题[8-9],最优regular‒vine Gaussian copula 作为一种以双变量pair‒Gaussian‒copula为基础模型的特殊的vine Gaussian copula模型,可以将高维Gaussian copula函数分解为多个pair‒Gaussian‒copula函数的结合,提高了模型的拟合度。C/D‒ vine Gaussian copula模型是特殊的R‒vine Gaussian copula模型,由于遍历性弱,其也只适合于随机变量个数较少的情况。因而建立适合于高维随机变量的最优R‒vine Gaussian copula建模方法还需要展开深入研究。
本文以服役大跨桥梁主梁为研究对象,基于主梁多个控制监测点(对应多个监测变量)的日常极值应变监测数据,首先,引入双变量pair‒Gaussian‒copula模型,实现多个监测点相依结构的变量分离,进而,结合最优R‒vine 理论,建立刻画监测变量间相关性的最优R‒vine Gaussian copula模型及其对应的R‒vine矩阵;然后,基于控制监测点的功能函数,对各监测点失效模式相关性进行建模分析,结合一次二阶矩方法,对失效模式相关的大跨桥梁主梁进行失效分析;最后通过在役桥梁监测数据进行验证分析。
1 监测变量的最优R‒vine Gaussian copula模型及其对应的R‒vine矩阵
大跨桥梁主梁包含多个应变监测点,考虑到动态监测日常极值应变的随机性,每个监测点的应变被认为是一个监测变量,因而多个监测点对应多个监测变量。由于具有共同输入随机源(共同的环境荷载与车辆荷载),这些监测变量相互之间存在非线性相关性[1~7]。引入pair‒Gaussian‒copula 理论和二维Gaussian copula 理论建立刻画这些相关性的最优R‒vine Gaussian copula 模型及其对应的R‒vine矩阵。
1.1 Pair-Gaussian-copula理论
Bedford 等[8~9]提出了基于pair copula 构造模块的多元随机变量联合概率分布模型。Pair copula 构造模块为多维随机变量提供了一种分离变量间相依结构的方法,可以将多维随机变量按照某种逻辑结构分解为多个两两变量的pair copula模块,为copula理论在高维随机变量的应用提供了理论基础。
将桥梁主梁n个监测点所对应的监测极值应变定义为一个n维随机变量X=(x1,x2,…,xi,…,xn),基于copula 模型的联合概率密度函数为f(x1,x2,…,xi,…,xn),按照条件密度函数理论可以写为

式中:c 为copula 密度函数;Fi(xi)和fi(xi)分别为随机变量xi的边缘概率分布函数和概率密度函数。
由式(1)可得二维随机变量的联合概率密度函数为
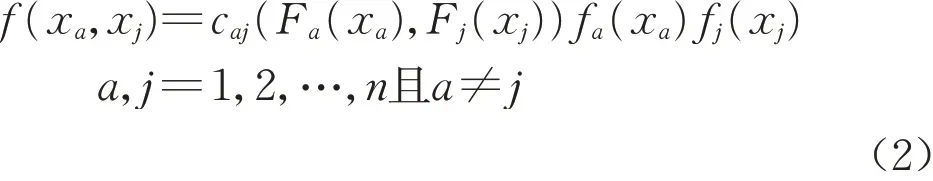
式中:caj(Fa(xa),Fj(xj))为xa和xj的二维copula 密度函数。
由式(2)可得,在xj已知的条件下,xa的概率密度函数为

由式(3)可得,在n维随机变量u已知的条件下,任意随机变量x的条件密度函数为
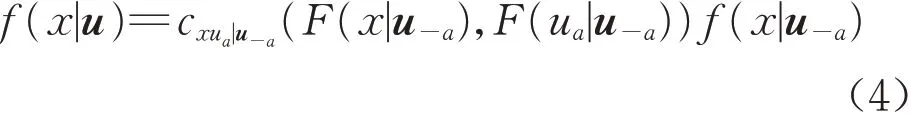
式中:ua为n维随机变量u中的一个分量;u-a为n维随机变量u 中去掉ua之后的n-1 维分量;cx,va|v-a=应的pair‒copula 密度函数,结合式(4),随机变量x的条件分布函数可以表示为

其中,当v为单个变量时,F(x|v)可以简化为
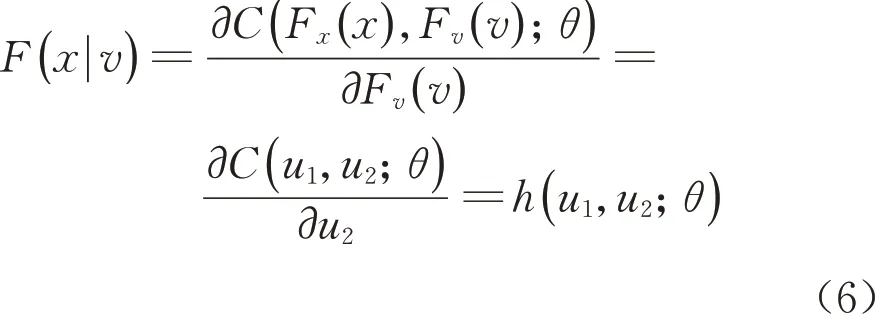
式(5)、(6)中:u1=Fx(x)和u2=Fv(v)分别为x 变量和v变量对应的边际累积分布函数。
式(7)和式(8)分别表示二元Gaussian copula概率分布函数和二元Gaussian copula 概率密度函数。


式中:ui=Fi(xi),i=1,2,Fi(xi)是xi的边缘概率分布函数;ΦG为Gaussian copula 函数;Φ 为标准正态分布函数;Φ-1为Φ 的逆函数;r=Φ-1(u1);s=Φ-1(u2);ρ 为copula 函 数的 相 关 参数,ρ ∈[-1,1]。
1.2 最优R-vine Gaussian copula 模型及对应的R-vine矩阵
多元随机变量不同的排列顺序对应着不同的多元分布结构,Bedford 等[8~9]引入vine 来对多元随机变量的分解结构进行描述,其中,性能最好的是最优R‒vine结构。
1.2.1 R‒vine Gaussian copula模型
R‒vine Gaussian copula 模型就是利用pair‒Gaussian‒copula模型作为基础模块对多元随机变量以一列树集的形式进行分层分解。对非空有限点集V,令维数d=|V|,则在V 上定义的R‒vine 是一列树集υ=(T1,…,Tn-1),其中T1=( V1,E1,Tn-1)=(Vn-1,En-1),V1=V,Vi=Ei-1(i≥2),即:树Ti的点 是Ti-1的 边,用{v,w}表 示Ti的 一 条 边,即Ei⊆{{v,w}|v ≠w ∈Vi},v中的每棵树Ti满足邻近条件。
对于n维随机变量X=(X1,…,Xn),第i个随机变量的边缘高斯密度函数为fi,对应的R‒vine Gaussian copula联合密度函数为

式中:E={E1,E2,…,En-1}为边集;为Ei中的一条边;cv,w|D(e)为对应的pair‒Gaussian‒copula 密度函数,其中v,w 为边e 相连接的两个节点,D(e)为条件集;F(xv|xD(e))和F(xw|xD(e))为条件高斯概率分布函数,利用式(4)~(6)可递推得到。
1.2.2 R‒vine 结构的构建方法
在随机变量个数较少的情况下,可以通过遍历所有的R‒vine 结构,结合观测数据选取最优R‒vine结构,但是一旦变量个数较多时,R‒vine结构数量会急剧增加。Nápoles等[10]指出,在考虑不同变量所对应的节点顺序情况下,d 维随机变量的R‒vine 结构有种。因此本文通过最大生成树(MST‒PRIM)算法[11]来选择最优R‒vine 结构,构建过程如下。
(1)计算两两变量之间的Kendall 秩相关系数,通过最大化Kendall 线性相关系数绝对值之和D 来选择R‒vine结构的第1棵树,即

式中:δv,w为变量v(节点)和变量w(节点)对应Kendall秩相关系数;Ei为第i棵树的边集。
(2)基于节点之间变量对的分布,确定每条边对应的pair‒Gaussian‒copula 模型,且对其函数的参数进行估计。
文中基于Kendall秩相关系数对Gaussian copula模型相关参数进行估计,Kendall 秩相关系数是Gaussian copula 函数常用的相关性测度,常见的二元Gaussian copula相关参数与Kendall秩相关系数τk之间的关系见文献[11-12]。
(3)上一层树每条边对应的变量对,作为下一层树的节点,重新根据MST‒PRIM算法确定下一层对应的树结构和pair‒Gaussian‒copula模型。
(4)重复步骤(3),直到节点数目为2,即完成R‒vine结构的构建。
以5 维监测随机变量为例,构建其对应R‒vine结构如图1 所示。由图1可知,5 维监测随机变量R‒vine 结构有4 棵树、5 个节点,节点之间的连线叫做边,共有10 条边,每条边对应一个pair‒copula 模型,其中“|”线之后的变量代表的是条件变量。
为方便表示联合密度函数的分解形式,Nápoles等[10]提出利用约束矩阵M=(mi,j)i,j=1,...,n来储存R‒vine的所有树和边的集合υ,这样每一个条件分布可以根据约束集集合CM=CM(i)∪...∪CM(d-1)来表达,其中第i(i=1,…,n-1)个约束矩阵集表示为

式中:mk,i为矩阵M中k行i列对应的节点;{mi,i,mk,i}称为被条件集;D为条件集。
1.2.3 最优R‒vine Gaussian copula 模型和对应最优R‒vine矩阵的构建方法
根据Bedford 等[9]的推导,运用约束集矩阵的符号表示,可得随机向量x=(x1,x2,…,xn)的最优R‒vine Gaussian copula 联合密度函数为一系列pair‒Gaussian‒copula 和边缘密度函数之积,如式(12)所示。
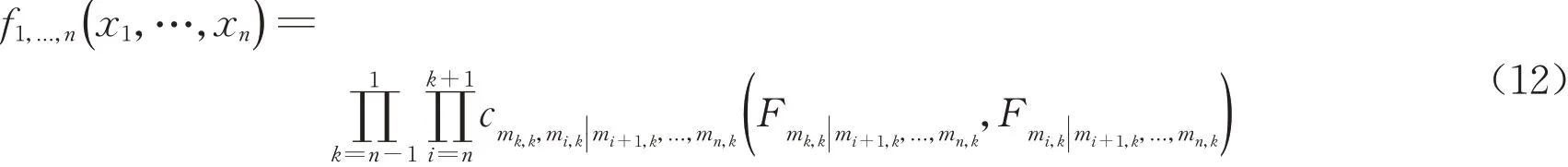
式 中:mk,i为 矩 阵M 中k 行i 列 对 应 的 节 点,Fmk,k||mi+1,k,...,md,k和Fmi,k||mi+1,k,...,md,k为mk,k和mk,i对应的条件高斯概率分布函数,由式(4)~(6)可递推得到。

式(13)的具体构造步骤是:将第1 棵树的节点排列在主对角线上,主对角线上第1 个节点和矩阵最后1 行的节点构成第1 棵树的边,如(5,1)、(4,2)、(3,2)、(2,1)是第1棵树的边;主对角线上第1个节点和倒数第2 行的节点以矩阵最后1 行节点为条件构成第2 棵树的边,如(5,2|1)、(4,3|2)、(3,1|2)是第2棵树的边;主对角线上第1个节点和矩阵倒数第3行的节点以矩阵最后2行为条件构成第3棵树的边,如(5,3|1,2)、(4,1|2,3)是第3棵树的边;以此类推即可得到R‒vine结构。
2 失效模式非线性相关的在役桥梁主梁失效概率分析
基于监测变量非线性相关性R‒vine Gaussian copula 模型,多个监测点失效模式非线性相关性模型可利用两两监测点失效模式间的二元失效模式pair‒Gaussian‒copula 模块,通过最优R‒vine 结构来建立。利用所建立的最优R‒vine Gaussian copula模型可实现失效模式相关的桥梁主梁失效概率分析,核心流程详细步骤为:①基于混凝土的容许应变和监测极值应变信息(拉应变为正,压应变为负),采用一次二阶矩方法,计算监测点可靠指标和失效概率;②基于监测点失效概率,采用pair‒Gaussian‒copula 理论,进行任意2 个监测点及其失效模式非线性相关的主梁失效概率分析;③基于任意2个监测点失效模式非线性相关的主梁失效概率分析结果,基于所建立的最优R‒vine Gaussian copula模型,采用串联结构体系可靠性分析方法,进行多个监测点失效模式非线性相关的大跨桥梁主梁失效概率分析。
2.1 桥梁主梁监测点可靠指标计算
采用一次二阶矩方法[13-14]进行桥梁主梁监测点可靠指标的计算,桥梁监测点极限状态方程为

式中:R 为容许应变;S 为极值应变。R 与S 相互独立。
监测点可靠指标计算公式为

式中:μS、σS分别为截面监测点极值应变的平均值与标准差;μR、σR分别为容许应变的平均值和标准差。极值应变指每天监测应变绝对值的极大值,监测的拉应变为正,压应变为负。
2.2 考虑两个失效模式相关性的主梁失效概率分析
Pair-copula 模块中的二元结构体系有2 种形式:串联体系和并联体系。任意2 个监测点形成的二元组合结构体系是并联体系[1-2,5],即本文R‒vine结构中任意一条边的两个点之间呈并联关系。根据文献[2]可知,n 维并联结构体系的失效模式功能函数为
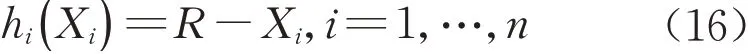
式中:n为监测点总数;i为第i个监测点;Xi为第i个监测点的极值应变。
基于式(7)、(8)和式(14)~(16),可得pair‒Gaussian‒copula模块中任意二元结构体系失效模式同时发生的概率为
计算了3个模型得到的碎片最终速度与数值模拟得到的碎片最终速度之比。3个模型计算得到的装药比比值误差的比较如图6所示。可以看出,模型2确实明显偏离数值模拟结果,而模型1和模型3在跳跃变化的区段(装药比为0.657%~0.792%),理论模型与数值计算相比没有明显的差别。但是随着装药比的增大,模型1和模型3的结果与数值模拟结果之间的偏差越来越大。相对而言,模型3是基于动量守恒的3阶段计算模型,其结果与数值模拟结果最为接近,δ在10%以内。说明,对于小装药比爆炸驱动双层壳体的情况,单纯基于Gurney公式的直接应用要谨慎,发展两段驱动理论模型进行碎片速度的估算是有必要的。

式中:i,j ∈{1,2,…,n}且i≠j;Xi为第i 个监测点的极值应变;和pfj为监测点的失效概率,可以由式pf=Φ(-β)得到,β为可靠指标。
2.3 多个监测点失效模式非线性相关的桥梁主梁失效概率分析
假定桥梁主梁任意2个监测点非线性相关的二元结构体系呈串联关系,结合式(17)可得多个失效模式非线性相关的桥梁主梁失效概率为

多个失效模式相互独立的桥梁主梁失效概率为

式中:pfi是第i个监测点的失效概率。
肇庆西江大桥为大跨度连续刚构组合梁桥,主桥上部结构为预应力混凝土桥‒连续箱梁组合体系[15~16]。采用第5跨顺桥向5个截面(A,B,C,D,E)的健康监测数据对第5 跨主梁进行失效概率分析。截面位置及传感器布置如图2、3 所示,其中截面A对应传感器1和传感器2,截面B对应传感器3和传感器4,截面C对应传感器5和传感器6,截面D对应传感器7和传感器8,位置与截面B相同,截面E对应传感器9 和传感器10,位置与截面A 相同。利用这10 个传感器采集得到的混凝土极值应变数据对第5跨主梁的失效概率进行分析。采集得到的应变数据信息包含了车辆荷载、温度荷载、收缩徐变、结构自重以及结构变化的信息。
在不考虑监测点失效模式相依性的情况下,10个监测点的最大失效概率认为是第5跨主梁的失效概率,由式(17)进行计算。在考虑监测点失效模式相依性的情况下,所有任意组合模块(pair‒Gaussian‒copula 模块)中的最大失效概率认为是第5 跨主梁的失效概率,由式(18)进行计算。

图2 西江大桥监测截面分布(单位:m)Fig.2 Layout of monitored section of Xijiang Bridge(unit:m)

图3 截面A、B以及C的传感器布置Fig.3 Layout of sensors on sections A,B,and C
对肇庆西江大桥跨中顺桥向5 个截面进行了100 d的监测,保证了10个监测点监测应变的概率统计特性得到正确提取。10个监测点的监测极值应变时程曲线如图4所示。
对监测点的极值应变数据采用五点三次平滑进行处理,处理之后的数据被认为是构建最优R‒vine copula模型的初始状态数据。基于桥梁截面各监测点失效模式非线性相关的最强相依关系,采用最优R‒vine Gaussian copula 模型对第5 跨主梁失效概率进行分析。
基于各监测点对应的监测极值应变数据可得各监测变量之间的秩相关系数,通过最大生成树MST‒PRIM 算法,确定Kendall 秩相关系数绝对值最大的双变量,选择的双变量分别是5‒1、1‒3、3‒9、7‒9、9‒2、10‒2、8‒2、2‒4、4‒6,从而确定R‒vine 的第1 棵树形结构图,如图5所示。
类似地,依据监测变量间的最强相依关系,通过最大生成树MST‒PRIM 算法可以得到R‒vine 的另外8 棵树的结构,从而得到R‒vine 矩阵,如式(20)所示。

分别对截面的初始状态信息进行Kolmogorov‒Smirnov(K‒S)检验,10个传感器对应监测变量的均值、标准差和p 值如表1 所示,其中,p 值表示观察到与原假设下(正态分布)的观测值相同或更极端的测试统计量的概率,当p 值小于0.05 时,认为原假设(正态分布)不成立。由表1 可知,各监测极值应变在5%显著性水平上不能拒绝原假设(服从正态分布),即接受服从正态分布。因此,认为10个监测点的极值应变数据均近似服从正态分布。肇庆西江大桥混凝土容许压应变服从均值为1597.68×10-6、标准差为175.74×10-6的正态分布(变异系数取值0.11[15-16])。因而,采用一次二阶矩方法对监测点可靠指标进行计算。
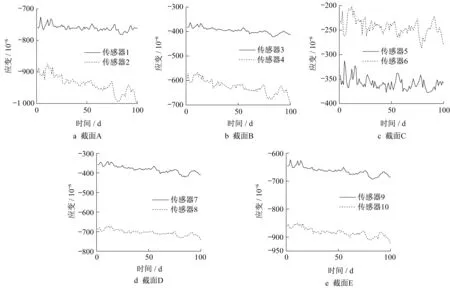
图4 5个截面监测极值应变时程曲线Fig.4 Monitored extreme strain curves of five sections
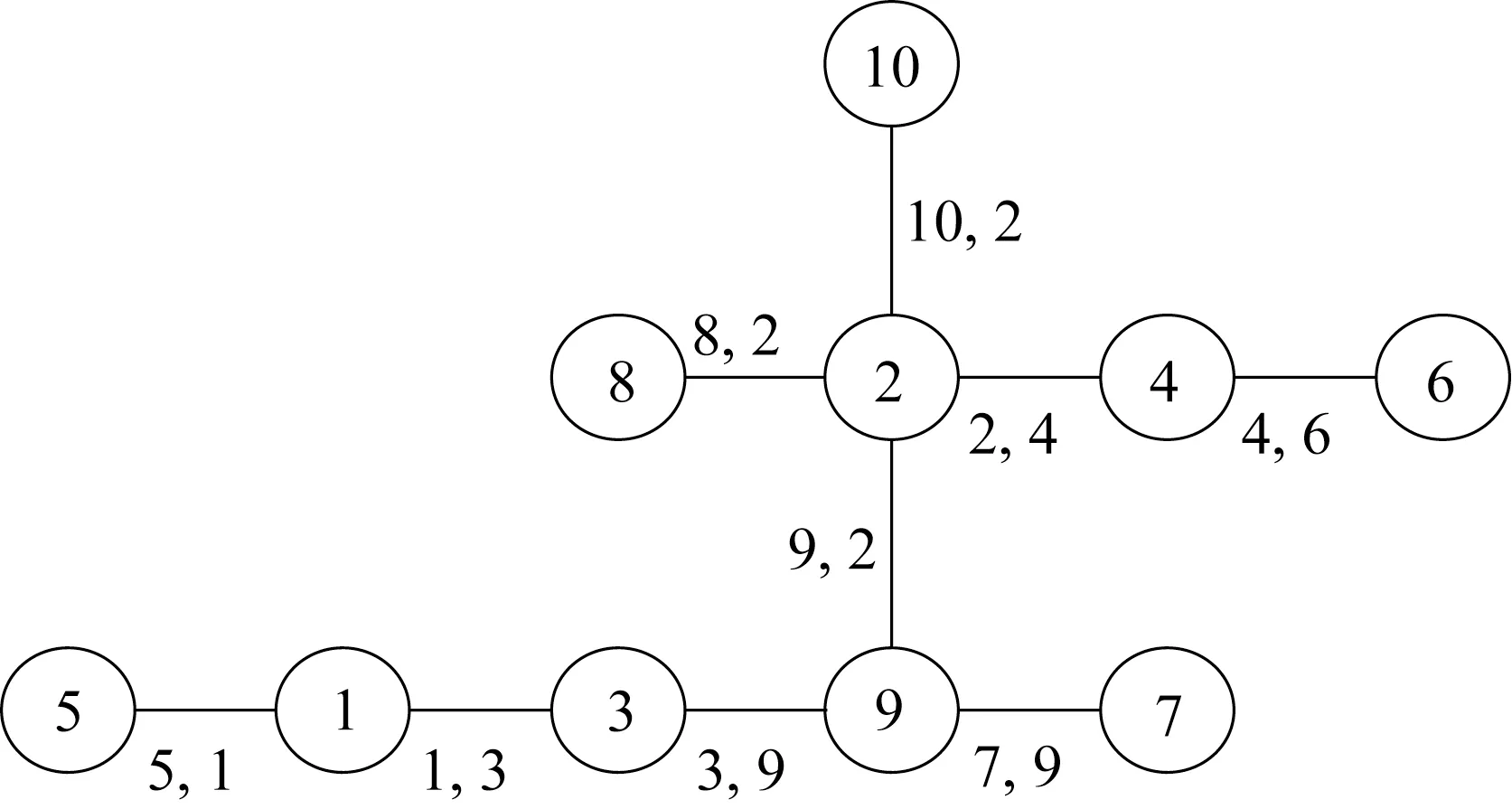
图5 R-vine的第1棵树形结构图Fig.5 First tree of R-vine structure
基于表1,结合式(12)和式(13)可得监测点可靠指标为

式中:μ和σ分别为监测点极值应变绝对值的平均值与标准差。
肇庆西江大桥第5 跨主梁顺桥向截面A、B、C、D、E 所对应10 个监测点的可靠指标和失效概率如表2所示。从表2中计算结果可知,同一截面的不同测点(顶部和底部)对应的可靠指标和失效概率会出现差异性较大的结果,这主要是由于预应力混凝土结构在预应力和荷载共同作用下,同一截面顶、底板位置的应力状态不同。

表1 各监测点变量对应的均值、标准差和p值Tab.1 Mean,standard deviation and p-value of multiple monitored variables
结合表2,利用式(19)可得不考虑失效模式相关性的第5跨主梁失效概率为

基于确定的最优R‒vine 矩阵(式(20)所示)和pair‒copula失效模块,通过二元Gaussian copula对考虑失效模式非线性相关的第5跨主梁失效概率进行分析。基于构建的R‒vine copula 模型,桥梁截面的10 个监测点可以分解为45 个两两结构相依的失效模块。各失效模块对应的失效概率如表3所示。
由表3 可得,第5 跨主梁所对应的10 维随机变量各组合模块失效模式的失效概率,根据式(18)可得,考虑失效模式非线性相关的第5 跨主梁失效概率为

表2 各监测点对应的可靠指标和失效概率Tab.2 Reliability index and failure probability of multiple monitoring point
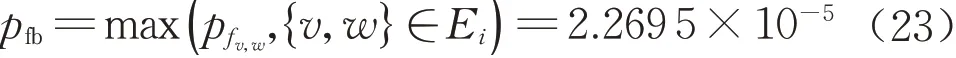
式中:pfv,w表示v 节点和w 节点的pair‒copula 模块的失效概率;Ei(i=1,…,9)为表3 中第i 棵树的边集。
由式(22)和式(23)计算结果可知,采用最优R‒vine Gaussian copula 模型,肇庆西江大桥第5 跨主梁考虑失效模式相关性的失效概率要小于不考虑失效模式相关性时的失效概率。式(22)和式(23)计算结果的差异性与文献[1]建立的C/D‒vine Gaussian copula 模型计算结果的差异性相比(文献[1]中不考虑失效模式相关性的失效概率为1.06×10-2,采用C/D‒vine Gaussian copula 模型考虑失效模式相关性的失效概率为1.6×10-3和1.7×10-3,考虑与不考虑失效模式相关性计算结果的差异性偏小,说明C/D‒vine Gaussian copula 考虑的相关性偏小),进一步验证了本文最优R‒vine copula 模型的准确性。而且,文中采用的最优R‒vine Gaussian copula 模型是根据变量间相依性特征来决定其相依结构的形式,与文献[1]事先设定树结构形式而建立的C/D‒vine Gaussian copula 模型相比,在变量间相关性建模上拟合效果更佳,且更符合变量间的实际情况。

表3 各失效模块对应的失效概率Tab.3 Failure probability of multiple pair-Gaussian-copula

续表
4 结论
(1)给出了大跨桥梁主梁多个控制监测点监测数据之间最强相关性的最优R‒vine 分析方法,解决了高维随机变量遍历性复杂的特点。
(2)提出了大跨桥梁主梁失效概率分析的最优R‒vine Gaussian copula数据融合方法。
(3)为考虑高维随机变量相关性和多个监测点失效模式相关性的大跨桥梁主梁失效概率分析提供了一种新思路,为在役桥梁安全评价提供了理论基础和应用方法。
作者贡献说明:
刘逸平:指导结构健康监测。
肖青凯:数据分析,撰写论文初稿。
杨光红:协助完善研究内容。
刘月飞:修改完善数学理论。
樊学平:指导论文总体框架,定稿。

