交叉积C*-代数Cuntz半群的性质

杨 君，方小春，范庆斋

（1. 同济大学数学系，上海200092；2. 上海海事大学数学系，上海201306）

Connes［1］对于拓扑群作用在von Neumann 代数上引入了Rokhlin 性质。之后，Herman 等［2］对于拓扑群作用在UHF‒代数引入了Rokhlin 性质，Rordam［3］、Kishimoto［4］对于拓扑群作用在一般的C*‒代数引入了Rokhlin 性质，Phillips［5］对于有限群作用在单的C*‒代数上引入了迹Rokhlin性质。

本文研究有限群G作用在有单位元单的C*‒代数上，并且群作用具有迹Rokhlin 性质（Phillips 提出的），得到的交叉积C*‒代数的Cuntz 半群的性质的如下结论：

定理1 A 是一个无限维有单位元单的具有k‒局部几乎可除性质的C*‒代数。α：G →Aut(A)是有限群G 作用在C*‒代数A 上，并且作用具有迹Rokhlin 性质。则交叉积C*‒代数C*(G，A，α)具有k‒局部几乎可除性质。

定理2 A 是一个无限维有单位元单的满足UCF Pn(W(A))=m 的C*‒代数。α：G →Aut(A)是有限群G 作用在C*‒代数A 上，并且作用具有迹Rokhlin 性质。则交叉积C*‒代数C*(G，A，α)满足UCF Pn(W(C*(G，A，α)))=m。

为了证明上述定理，利用Lin［6］提出的迹逼近C*‒代数的概念。

设Ω是一类C*‒代数，则由Ω中的C*‒代数迹逼近之后得到的C*‒代数类记为TA Ω。

一个有单位元单的C*‒代数A属于TA Ω，是指对于任意的ε ＞0，任意的有限子集F ⊆A，任意的a≥0，存在一个投影p∈A和A的C*‒子代数B满足1B=p并且B∈Ω，使得

（1）对于任意的x ∈F，‖xp-px ‖＜ε。

（2）对于任意的x ∈F，pxp∈εB。

（3）1-p Murray-von Neumann 等价于- -----aAa 中的投影。

准确地说，证明定理1和定理2 分为两步。

第一步，证明如下性质能够由Ω 类中C*‒代数遗传到由Ω类中C*‒代数迹逼近之后得到的C*‒代数类中，也就是TA Ω中。

（1）k‒局部几乎可除性质。

（2）UCF Pn(W(A))=m。

第二步，利用Fan等［7］得到的如下结果：

Ω是一类有单位元的C*‒代数，Ω类中C*‒代数对于可传的有单位元的C*‒子代数和张量上矩阵代数是封闭的。A∈TA Ω 是一个无限维有单位元单的C*‒代数。α：G →Aut(A)是有限群G作用在C*‒代数A上，并且作用具有迹Rokhlin性质。则交叉积C*‒代数C*(G，A，α)也在TA Ω中。

由上述两步，可以得到定理1和定理2。本文中证明第二步。

1 预备知识

2 主要结果

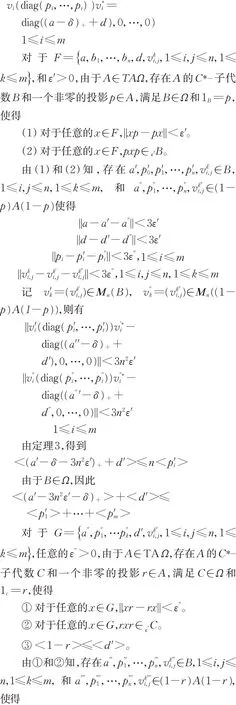
下面给出定理1的证明。

证明：由引理2，定理5和定理6可以得到。

作者贡献说明：

杨 君：具体撰写论文。

方小春：提出研究选题。

范庆斋：参与讨论研究。