基于驾乘人员热感觉的车内空调送风参数设计

赵兰萍，郑振鹏，，徐 鑫，杨志刚

（1. 同济大学机械与能源工程学院，上海201804；2. 同济大学上海市地面交通工具空气动力与热环境模拟重点实验室，上海201804）

车内热环境直接影响驾乘人员热感觉，不舒适的热环境会使驾驶员的驾驶专注度下降，发生交通事故的概率增加［1］。传统燃油车中空调系统能耗约占燃油总消耗的5.0%～10.0%，而在电动汽车中，空调所消耗的能量占整车总能耗的比例则高达18.0%～53.7%［2-4］。传统的汽车乘员舱空调送风参数的设计和考核往往基于乘员呼吸点位置的空气温度或乘员舱平均温度［5］，无法对车内的热环境和能耗进行精确控制。为了发展更为有效的汽车空调控制技术，需要采用合适的车内乘员热舒适性评价方法。国内车用空调领域目前较多采用经典的平均热感觉（PMV）评价方法［6］，由于该方法是针对稳态均匀的热环境而提出的，无法对车内热环境和乘员热舒适状态做出客观评估。等效均匀温度（EHT）评价方法［7］和Berkeley 评价模型［8］是两个具有代表性的不均匀热环境评价方法，欧洲车企较多采用其中的EHT 评价方法。已有学者对不同评价方法进行了对比研究，如文献［9］采用EHT和PMV评价方法进行汽车乘员热舒适评价，并与主观问卷调查结果进行对比分析。Zhang 等［8］则基于Berkeley 评价模型研究了空调送风条件和太阳辐射对人体生理参数及热舒适状态的影响。未见有文献同时基于不同的评价方法设计车内空调送风参数，对比分析所对应的人体热反应和热舒适指标等参数之间的区别。

本文采用计算流体力学（CFD）方法结合人体热调节模型进行人体热舒适性的仿真分析，通过最优拉丁超立方法建立样本数据库，用径向基神经网络模型（radial basis functions，RBF）建立近似模型，得到了包括送风参数及太阳参数在内的5个车内热环境影响因素与乘员生理参数及热舒适性指标之间的关系。在此基础上，基于EHT及PMV评价方法，通过序列二次规划优化算法（NLPQL），对冷但舒适、舒适和热但舒适3种设计需求下的车内空调送风参数进行了设计，分析对比了所对应的人体各主要生理参数及空调负荷等参数。

1.1 CFD模型及验证

乘员舱几何模型由荣威350试验用车扫描后通过三维软件逆向建模并简化得到，为了使后续CFD仿真得到的热流场更加接近真实情况，尽可能地保留了乘员舱内部的主要几何信息，如方向盘、座椅以及中控台等结构，同时在驾驶员位置加入人体几何模型。计算模型如图1 所示，其中图1b 还同时给出了送风角度的示意图。图中的送风角度为空调送风的俯仰角，范围在0°～30°之间。

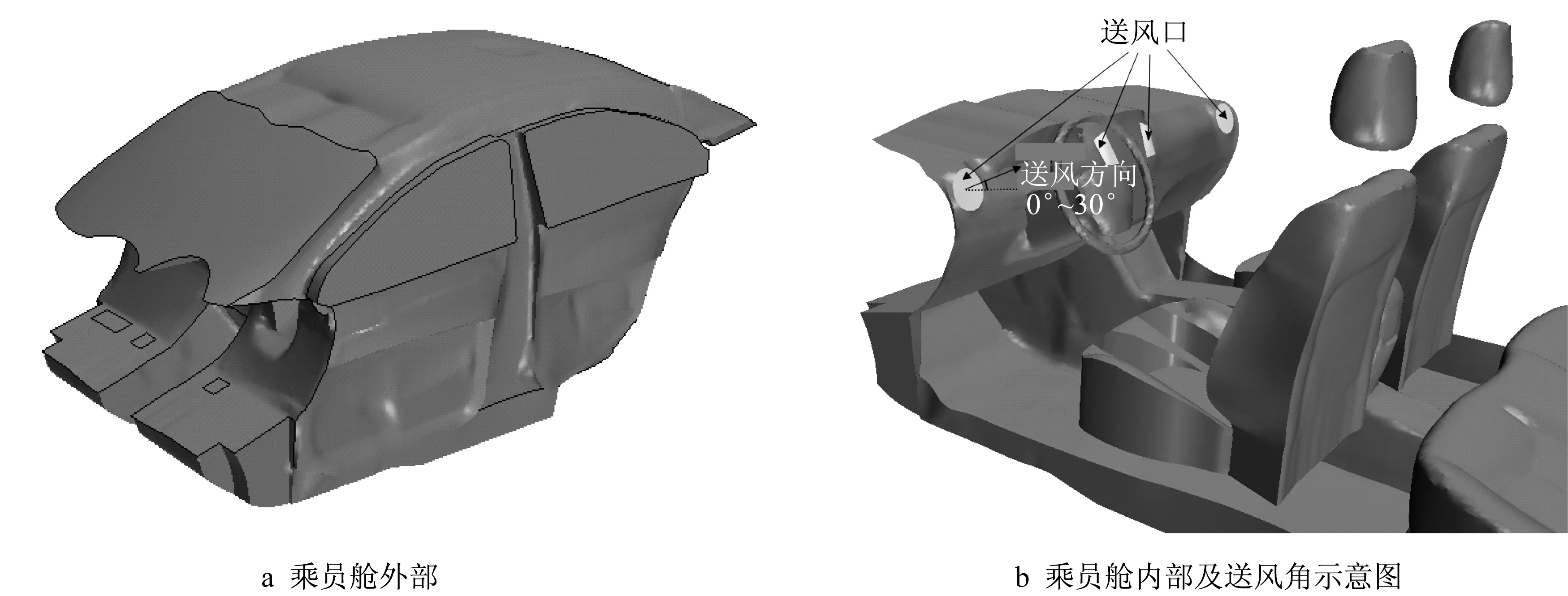
图1 乘员舱模型Fig.1 Cabin model

车内流场计算结合2 阶迎风格式［10-11］，采用Realizable k‒ε湍流模型。人体与周围热环境的辐射换热是其热感觉的重要影响因素，本文采用S2S（surface‒to‒surface）辐射模型，该模型仅考虑面与面之间的辐射传热，忽略介质之间的吸收、发射和散射。另外，为便于处理由于温差引起的空气浮升力的影响，采用Boussinesq 假设，该假设包括以下内容：①流体中的黏性耗散忽略不计；②除密度外其他物性为常数；③对密度仅考虑动量方程中与体积力有关的项，其余各项中的密度为常数。采用Stolwijk［12］提出的人体生理热调节模型，该模型分为被动系统和主动系统。模型将人体分为14个节段，每个节段又分为皮肤、脂肪、肌肉和核心共4 层。Stolwijk 模型能较好地模拟非均匀热环境下的人体皮肤热反应［13］。模型验证以单人驾驶员位置的车内热舒适实验为基础，边界条件的设置如下：空调送风速度、送风温度、车外空气温度、相对湿度、太阳辐射强度、太阳高度角与方位角等计算边界条件均采用实验测得的数据，设置送风口为质量流量入口，出口为压力出口，内壁面为耦合边界条件。

采用Hypermesh 软件生成面网格，再利用STAR‒CCM+软件生成边界层网格及体网格。共生成了5 套网格，网格数分别为210 万、320 万、400万、525 万和600 万。经网格无关性检验，发现当网格数大于400万后，继续增加网格数，各节段皮肤温度以及人体平均皮肤温度的仿真结果与实验值的偏差均小于1%。考虑计算资源，后续计算采用的体网格数量约为400 万。通过3 组实验与仿真结果的对比发现，人体各部位皮肤温度、车内壁面温度及空气测点温度的CFD 仿真结果与对应的实验测定值的偏差均在10%以内［14］。

1.2 样本选取方法

拉丁超立方设计的原理是在n 维空间中，将每一维坐标区间［Xkmin，Xkmax］，k∈［1，n］均匀等分为m个区间，每个小区间记为［Xki-1，Xki］，i∈［1，m］。随机选取m 个点，保证一个因子的每个水平只被研究一次，即构成n维空间，样本数为m的拉丁超立方设计。拉丁超立方设计相比正交设计法有着水平值分级宽松，实验次数可以人为控制等优点。但普通的拉丁超立方设计可能会存在实验点分布不够均匀的情况，随着水平数增加，丢失设计空间一些区域的可能性增加。本文选用最优拉丁超立方设计，使所有的实验点尽量分布在整个设计空间，具有更好的空间填充性和均衡性。表1中给出的各设计因素的取值范围根据上海地区夏季太阳辐射情况和车用空调常用送风参数范围确定。利用生成的60 个样本点进行CFD样本库的建立。

表1 设计因素范围Tab.1 Range of design factors

1.3 评价方法

图2 给出了等效均匀温度定义的示意图。图2中，ta为平均环境温度；-tr为环境的平均辐射温度；va为来流速度；teq为等效均匀温度；R为人体与壁面的辐射换热量；C为人体与周围气体的对流换热量。先设定一个空气流速为零、空气温度等于平均辐射温度的理想均匀环境。在衣着量和代谢强度相同的情况下，如果某非均匀环境下人体的显热损失与其在所设定的理想均匀环境下的显热损失相等，就称该均匀环境下的空气温度为非均匀环境下人体的等效均匀温度［14-15］。

图2 等效均匀温度（EHT）的定义Fig.2 Definition of EHT

EHT综合了人体与环境之间的显热交换（对流换热和辐射换热），可以用来衡量非均匀环境下人体的热舒适状态。Tanabe 等［16］通过暖体假人证明了用EHT 评价建筑内非均匀环境的人体热舒适是可行的。ISO 14505-2—2006［17］中则给出了如下人体各节段EHT的标准计算公式：

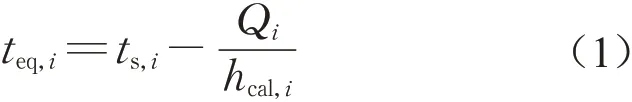
式中：teq，i为节段等效均匀温度，℃；ts，i为节段皮肤温度，℃；Qi为节段显热交换量，其中包括对流换热量及辐射换热量，W·m-2；hcal，i为等效均匀热环境及相同人体坐姿及服装条件下，人体节段表面的综合换热系数，W⋅m-2⋅K-1，可依据文献［18］中的关联式计算得到，计算结果如表2所示

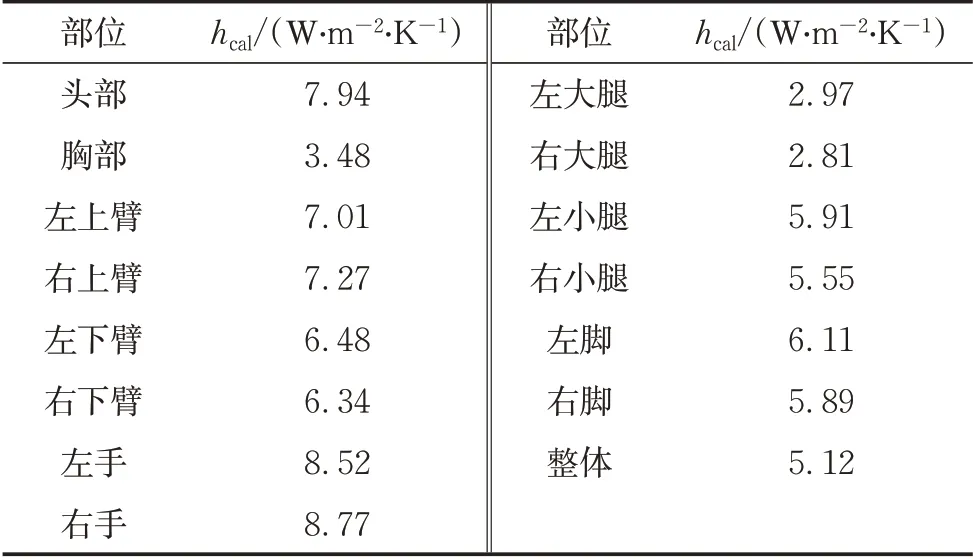
表2 h cal取值［18］Tab.2 Value of h cal

人体的平均等效均匀温度EHT 可以基于整体平均皮肤温度与整体总显热损失计算得到，其公式为

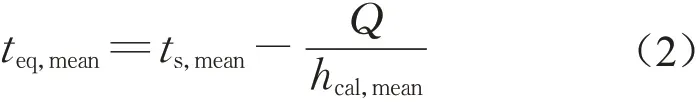
式中：teq，mean为人体平均等效均匀温度，℃；ts，mean为平均皮肤温度，℃；hcal，mean为平均表面综合传热系数，W⋅m-2⋅K-1；ts，mean可根据局部皮肤温度进行面积平均得到

式中：Ai为人体各节段的皮肤面积，m2。

Wyon结合人体主观评价实验得到了EHT热舒适区，Nilsson 则根据服装热阻的不同做了进一步的改进。热舒适分区如图3所示［19］。

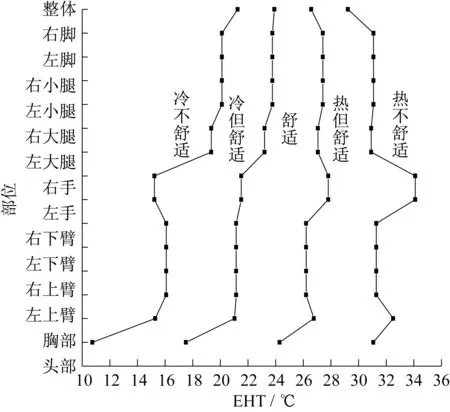
图3 EHT人体热舒适区Fig.3 Thermal comfort zone based on EHT

热舒适性理论认为，人是环境热刺激的被动接受者，通过人和热环境的热湿交换来影响人体生理参数，进而使人产生不同的热感觉。PMV的数学表达式是基于Fanger 教授的人体热平衡方程并结合Kanasa州立大学实验所得到的人体新陈代谢率及相应的主观热感觉数据而提出［20］。目前PMV 指标已被纳入ISO 7730标准，该指标综合考虑了环境空气温度、人体运动量、环境空气流速、太阳辐射，衣物热阻及空气相对湿度对人体热舒适的影响。

PMV指标中采用的American Society of Heating，Refrigerating and Air-Conditioning Engineers（ASHARE）七点式标尺则如表3所示。

表3 PMV热感觉标尺［21］Tab.3 PMV thermal sensation scale

本文将基于上述两种评价方法，对冷但舒适、舒适和热但舒适3 种需求下的空调送风参数进行设计。首先需要对两种评价方法的标尺进行折算。Gagge 等的研究结果发现，实际上人体不舒适表现在投票高于+2或低于-2的人身上，认为+2到-2的PMV指标区间为人体热舒适度的可接受范围［22］。将EHT舒适分区上的中线所对应的人体整体EHT与PMV标尺中的适中（0）相对应，定义为舒适状态；将冷但舒适的左边界所对应的人体整体EHT 与PMV 标尺中的冷（-2）相对应，定义为冷但舒适状态；将热但舒适区域的右边界所对应的人体整体EHT与PMV标尺中的暖（+2）相对应，定义为热但舒适状态。折算结果为：热感觉适中对应的PMV值及EHT值分别为0和25.3 ℃；热但舒适边界对应的PMV 值及EHT 值分别为+2 和29.2 ℃；冷但舒适边界对应的PMV 值及EHT 值分别为-2 和21.5 ℃。

1.4 近似模型及验证

在CFD样本计算结果基础上，采用径向基神经网络模型（radial basis functions，RBF）方法建立设计因素与目标因素之间关系的近似模型。RBF模型具有很强的逼近复杂非线性函数的能力，考虑到车内热环境及人体生理调节的复杂程度，采用该模型可以对样本点的仿真结果具有较好的拟合度。另外，RBF 模型相比于响应面模型、正交多项式模型和克里金模型等，其算法具有较好的泛化能力，同时具有学习速度快及较强的容错能力［23］。

以表1中的设计因素为输入，分别得到以EHT、PMV、人体对流换热量、人体辐射换热量、人体平均皮肤温度、人体显热换热量及人体总换热量等不同参数为输出的近似模型，所得到的近似模型对60个样本点的拟合确定系数R2都在0.99～1.00 的范围内。为了验证近似模型的预测精度，在样本空间外、设计因素范围内重新均匀抽取6个样本点进行仿真计算，计算结果作为近似模型的预测精度验证依据，所选6个样本点的具体参数如表4所示。

图4 为近似模型预测精度的验证结果。从图4可以看出，除了PMV 近似模型之外，其余近似模型的预测精度误差均值都在10%以内。PMV 近似模型，由于其输出值的量级较小，预测结果与仿真结果差0.3左右就会导致误差的百分比达到100%以上，所以该模型预测精度的验证效果不能简单依据误差百分比来进行评判，应参考误差绝对值。总体而言，所建立的各近似模型的预测精度较好。

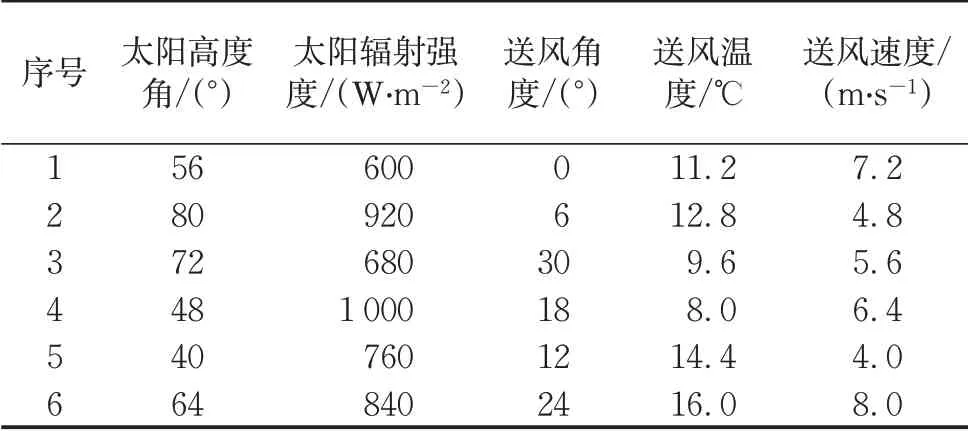
表4 近似模型验证用样本点Tab.4 Sample points for approximate model validation

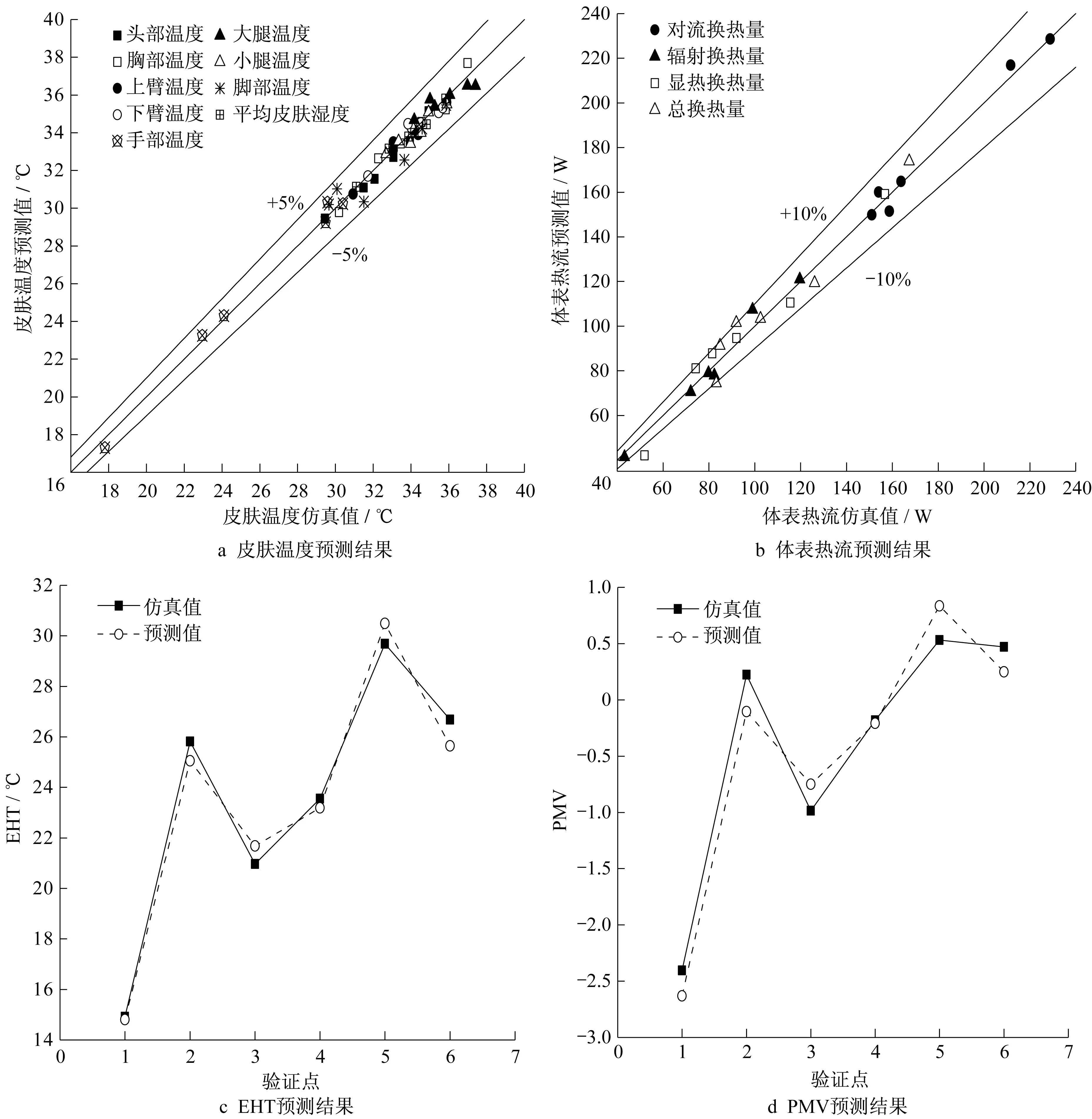
图4 近似模型验证结果Fig.4 Validation results of approximate models

2.1 送风参数

通过所建立的EHT 及PMV 近似模型，采用序列二次规划优化算法（NLPQL）进行送风参数的设计。NLPQL 算法是将目标函数以二阶泰勒级数展开，将约束条件线性化，通过解二次规划得到下一个设计点，然后根据两个可供选择的优化函数执行一次线性搜索，该算法的特点是较为稳定。设定太阳高度角为60°，太阳辐射强度为800 W⋅m-2，根据该算法，本文对不同热舒适设计需求下的空调送风参数进行了设计。表5给出了基于PMV及EHT评价方法的送风参数设计结果。由表5 可知，随着热舒适设计需求由偏冷向偏热的转变，空调的送风角度增加。在基于PMV方法的设计结果中，送风角度的增幅较大，而EHT方法所对应的送风角度基本维持在15°左右。送风角度的不同主要是由于EHT评价方法考虑了人体各部位的不同热敏感度，而PMV评价方法并没有这方面的考量。对比送风温度可以发现，随着热舒适设计需求由偏冷向偏热转变，空调送风温度明显增加，且PMV对应的送风温度的增幅更大，在偏冷或适中状态下，PMV 对应的送风温度低于EHT 的对应值，但在偏热状态下，则正好相反。在同一热舒适设计需求下，两种设计方法得到的送风速度的区别并不明显，而随着设计需求向偏热的转变，两者的送风速度差异变大。综合设计结果可以发现，送风温度与送风速度对人体的热感觉的确起到了较为关键的作用。基于EHT 评价方法的设计结果相较PMV评价方法而言，所设计出的空调送风状态更偏向高风温及高风速。

表5 送风参数设计结果Tab.5 Design results of air supply parameters

2.2 人体生理参数

依据表5 送风参数的设计结果，利用所建立的近似模型，进一步计算了不同热舒适设计需求下，人体表面的换热量及皮肤温度。图5为人体表面的换热量对比。规定人体向外界环境散发的热量为正，从外界环境中吸收的热量为负。从图5 可以发现，在热舒适设计需求为舒适但偏热的状态下，EHT设计法对应的对流换热量大于PMV 设计法所对应的值。结合表5 可知，两个评价方法对应的空调送风速度相差较大，EHT设计方法所对应的送风速度较大。在热舒适设计需求为舒适但偏冷的状态下，两种方法对应的空调送风速度相差很小，但送风温度相差较大，导致PMV设计方法对应的对流换热大于EHT 方法所对应的值。在热舒适设计需求适中的情况下，EHT方法对应的对流及辐射换热均略高于PMV方法对应的值，因而两者的显热交换量基本相等。潜热交换量方面，适中和偏冷但舒适的设计需求下，两种方法对应值相差不大，但在偏热但舒适的设计需求下，PMV 方法的对应值明显大于EHT 方法的对应值，说明此时PMV方法设计出来的热环境让人更容易出汗。同时可以发现，由于太阳辐射强度及太阳高度角维持不变，3类热舒适设计需求下的辐射换热变化很小，所以3 类需求下显热交换量的不同主要是由于对流换热的不同而导致。

图6为基于两种不同评价方法所设计的车内热环境下，人体表面总辐射换热量与对流换热量的比值对比。从图6 可以看出，随着设计需求由冷但舒适变为热但舒适，人体表面辐射换热占比在不断增加。EHT 设计方法对应的辐射换热占比的增幅小于PMV 方法的对应值。在偏冷及适中的热设计需求下，EHT 方法对应的辐射占比大于PMV 方法的对应值，但在偏热的热设计需求下，EHT 方法对应的辐射占比小于PMV方法的对应值，这是由于在该需求下，两者对应的辐射换热量相差不大，但PMV方法对应的对流换热量较小导致的。图7为基于两种不同评价方法所设计的车内热环境下，人体平均皮肤温度的对比。在热设计需求偏冷的情况下，EHT方法对应的平均皮肤温度更高，随着热设计需求向偏热转变，PMV方法对应的平均皮肤温度的增幅更大，最终导致在偏热的热设计需求下，PMV 方法对应平均皮肤温度比EHT 方法的对应值高1.19 ℃。

图8为3种不同热舒适设计需求下，两种设计方法得到的人体各节段皮肤温度的对比。从图8可以发现，在热舒适设计需求偏冷的情况下，EHT 方法对应的各节段皮肤温度均大于PMV方法的对应值，且身体上半部分的差异比下半部分的差异大。结合表5可以发现，这与EHT 设计方法的高送风温度有关，由于两者的送风角度均向上，因此主要区别在上半身。在偏热的设计需求下，由于风速较小但风温较大，PMV 方法对应的皮肤温度均大于EHT 方法的对应值，PMV方法温度最低的部位则由手变成了上臂，这是由30°的俯仰角导致的。同时可以发现，随着设计需求的变化，PMV方法相对于EHT方法，手部温度有着更大的变化。说明送风角度直接决定了气流的走向，对人体周围的流场和温度场有较大的影响。

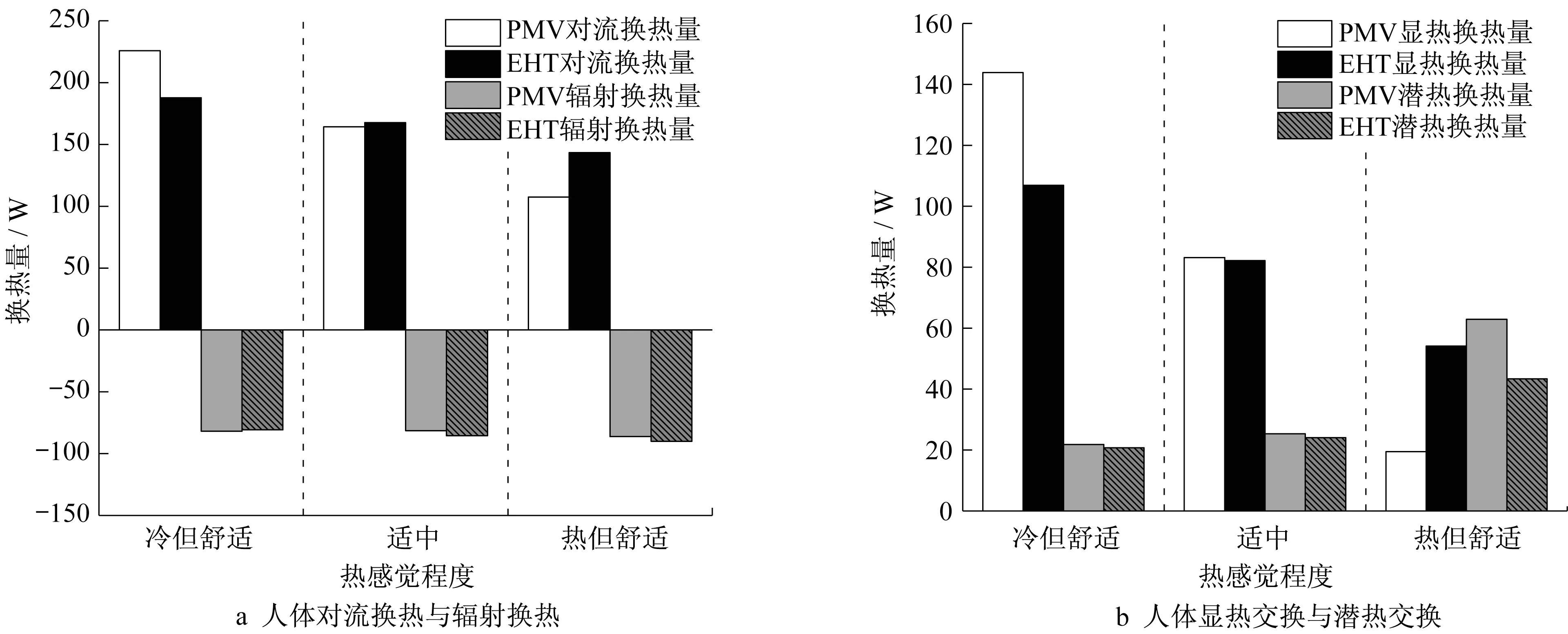
图5 不同评价方法的换热量对比Fig.5 Comparison of heat flux of different evaluation methods

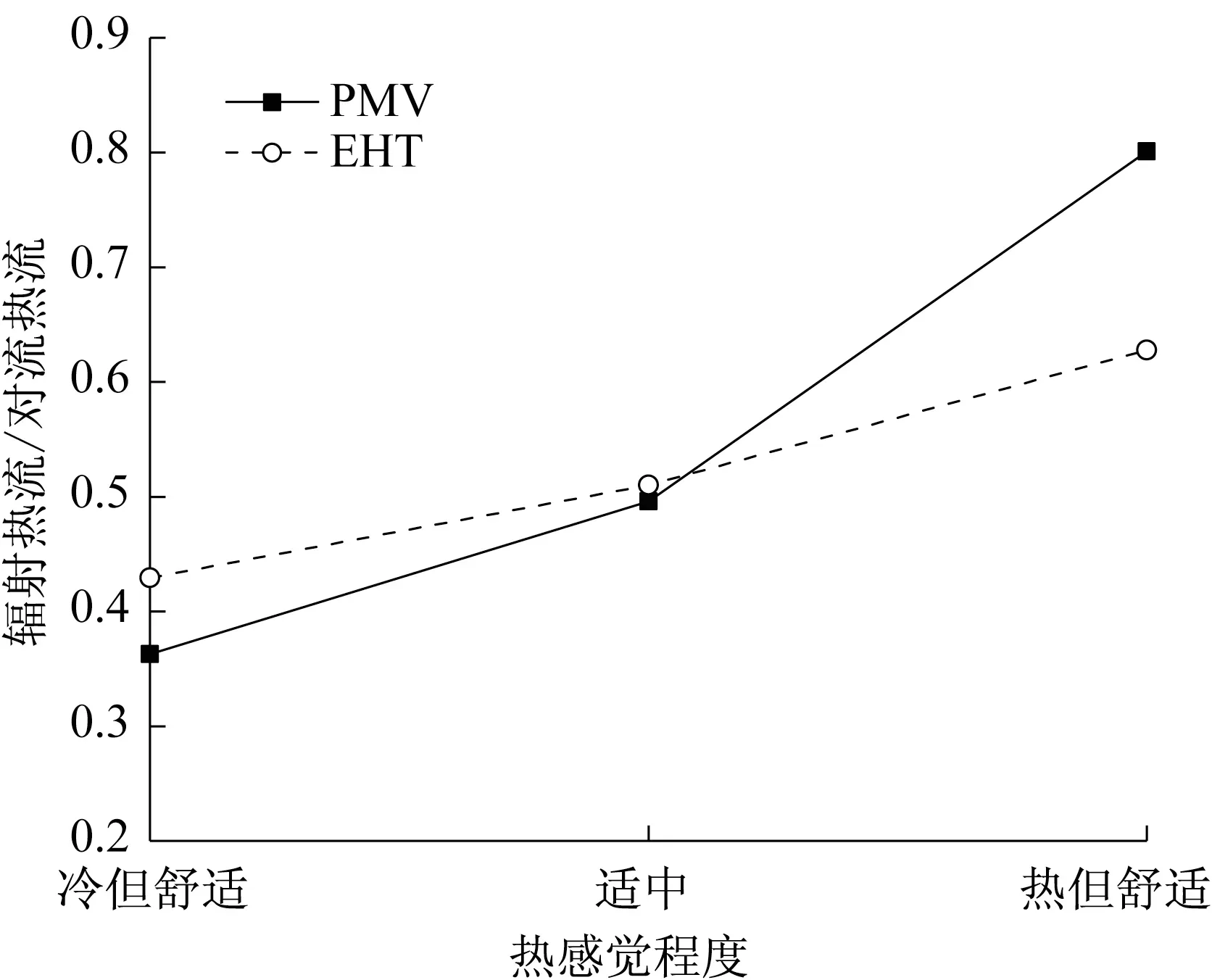
图6 辐射换热量与对流换热量之比Fig.6 Comparison of radiation proportion

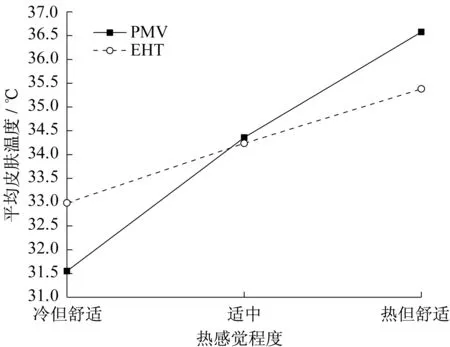
图7 平均皮肤温度对比Fig.7 Comparison of t s,mean

2.3 人体局部热舒适性

图9 为不同热舒适设计需求下，人体各节段的局部EHT值。结合图3的EHT人体热舒适分区，可以发现，在3个不同热舒适设计需求下，人体头部和手部的EHT值均比其余部位小，这意味着在同一需求下这两个部位的热感觉偏冷。同时，可以发现，当热舒适设计需求在偏冷或者适中状态下，PMV 及EHT两种方法对应的局部EHT值在人体下半身的节段上差别不大，但是在上半身各节段的EHT值差别较大。对于上半身节段，PMV 方法对应的EHT值偏离舒适区中线更远。从图9c可以看出，热舒适设计需求偏热时，PMV 方法对应各节段EHT 值均大于EHT方法，并且人体上半身的大部分节段处于不舒适状态。综合3 个不同热舒适设计需求，可以看出，对于同一热舒适设计需求，PMV 设计方法对应的各节段局部EHT 值偏离舒适区中线的距离更大，舒适度更差。

2.4 空调冷负荷

为简化起见，设空调为全新风外循环状态，空调冷负荷计算以空调出风口及车舱出风口的焓差为计算依据。图10a 为太阳高度角为60°，太阳辐射强度为800 W⋅m-2环境下，基于两种评价方法所设计出的热舒适状态适中时所对应的空调冷负荷。可以看出，两种评价方法对应的空调冷负荷基本相等。在偏冷但热舒适的设计需求下，PMV方法对应的冷负荷稍大，这主要由于PMV方法对应的空调送风温度较小导致的。在偏热但热舒适的设计需求下，EHT方法对应的冷负荷稍大，此时两种评价方法对应的送风温度差别较小，但EHT方法对应的送风速度明显大于PMV 方法的对应值。图10b 为适中但热舒适需求下空调冷负荷与太阳辐射强度的关系。可以看出，太阳辐射强度增大，空调冷负荷也以稳定的速度随之增加。当辐射强度在700～800 W⋅m-2之间时，基于两种方法设计的热环境的空调冷负荷基本相等，而在其他范围内，EHT 方法对应的空调冷负荷均小于PMV 方法的对应值。这是由于当太阳辐射大于800 W⋅m-2时，两者对应的送风速度接近，但是EHT方法对应的送风温度更高，故其空调冷负荷更小。当太阳辐射小于700 W⋅m-2时，此时EHT方法虽然有着更大的送风速度，但是两者的送风速度差异较小，送风温度的差异较大，最终导致了EHT方法对应的空调冷负荷小于PMV方法的对应值。

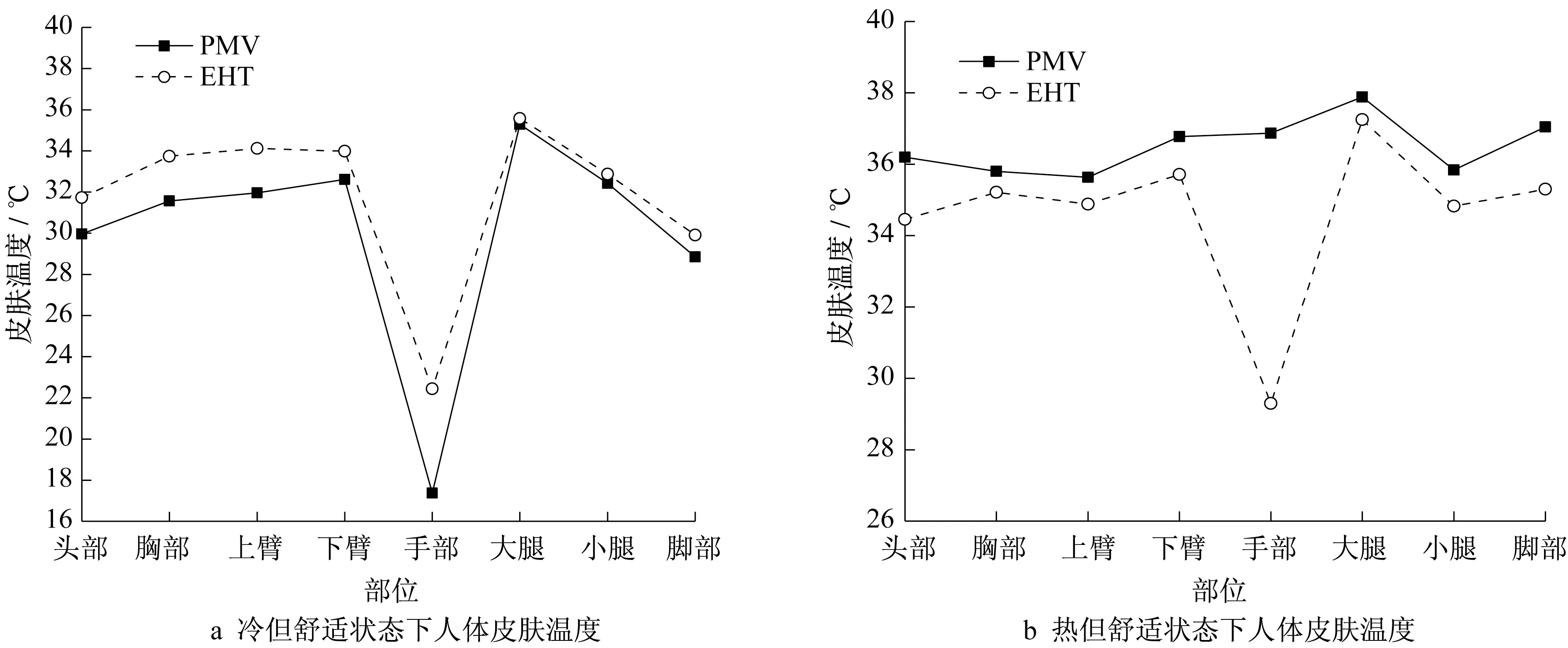
图8 不同评价方法的各节段皮肤温度对比Fig.8 Comparison of segment temperature of different evaluation methods

图9 不同评价方法的各节段EHT对比Fig.9 Comparison of EHT of each segment of different evaluation methods

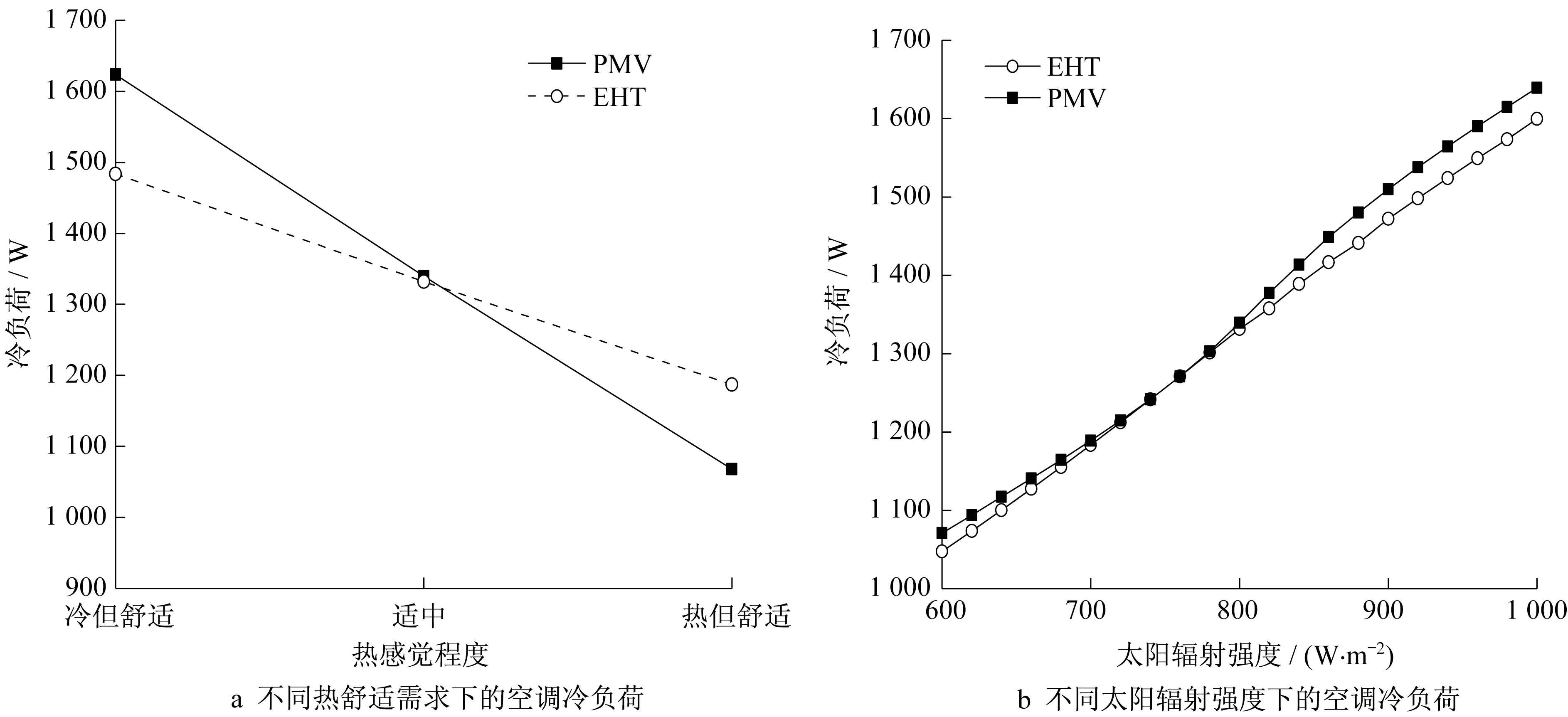
图10 不同评价方法的空调冷负荷Fig.10 Comparison of air-conditioning cooling load of different evaluation methods

3 结论

（1）随着热舒适设计需求由偏冷向偏热状态转变，PMV 方法主要靠同时改变空调送风温度、送风速度和送风角度来满足乘员热舒适性指标要求，而EHT方法则更多依赖送风速度的改变，送风角度和送风温度的变化均小于前者。同一热舒适设计需求下，基于EHT 评价方法的设计方法，更偏向高风温及高风速的空调送风状态。

（2）依据EHT 方法设计出来的车内热环境，人体皮肤温度随热舒适设计需求的变化较小。在偏热但舒适的设计需求下，PMV方法设计出来的热环境让人更容易出汗。

（3）在同一热舒适设计需求下，PMV 方法对应的各节段局部EHT值偏离舒适区中线的距离更大。由此可见，基于EHT 评价方法的热环境设计较PMV评价方法更容易满足乘员热舒适的要求。

作者贡献说明：

赵兰萍：理论指导，实验指导，文章结构搭建及调整，文字表达优化。

郑振鹏：近似模型建立，数值计算，文章内容撰写。

徐 鑫：仿真验证实验。

杨志刚：实验及计算资源提供。