基于双40英尺岸桥装卸的船舶多港主贝配载优化决策

张艳伟，马佳乐

（武汉理工大学物流工程学院，湖北武汉430063）

截至2019 年，我国集装箱吞吐量已增至26 107万TEU（国际标准箱）。集装箱贸易量的不断增长促进了海运船舶的大型化发展以及码头前沿装卸设备的更新换代。其中，双40 ft（1 ft=30.48 cm）岸桥为双吊具设计，通过吊具伸缩，单侧吊具可以吊取1个40 ft 箱、2 个20 ft 箱或1 个20 ft 箱（艏艉装卸）。船舶配载情况良好时，双吊具同时使用，一次装卸2个40 ft箱，若岸桥吊具对位亦满足要求，最多一次装卸4个20 ft箱。即理论上最多可以在一次作业中完成2 个40 ft 集装箱或4 个20 ft 集装箱的装卸，在降低船舶周转时间和提升码头装卸效率方面具备突出优势［1］，陆续被各大集装箱码头投入使用。

为充分发挥双40 ft 岸桥的效率，需尽可能保证岸桥双吊具的常见作业工况［2］，避免其余工况因频繁调节吊具浪费时间，但双40 ft 岸桥受其自身的限制，无法实现将2 个40 ft 集装箱同时装载到集装箱船不同层的两个箱位，因此，虽然双40 ft岸桥能够加快码头作业的速度，但同时亦对集装箱船配载计划提出了更高的要求。本文旨在提出适合多港口双40 ft 岸桥装卸的配载策略和模型，为船舶挂靠港双40 ft岸桥装卸提供条件，同时适用于普通岸桥作业。

多港集装箱船配载主贝计划问题（MP-MBPP），旨在将不同属性的集装箱划分箱组，实现箱组到船舶具体贝位的一一匹配，并运往后续港口，同时需兼顾船舶稳性、容量等条件。Wilson 等［3］为高效制定配载计划，提出采用分阶段法研究船舶全航线配载问题，并通过在目标函数中加入启发式规则得到较优配载方案，由于数学规划求解效率较低，仅得到了局部最优结果。Wilson等［4］提出了一种多港口运输集装箱船配载计划生成方法，同时考虑了各港口并行作业普通岸桥数量最大化问题。张维英等［5］采用多阶段法研究非混装情况下20 ft及40 ft标准箱的配载问题，在主贝计划中以贝位占用数量最少、倒箱量最少和集装箱船载箱率最高为目标，通过基于二叉搜索树算法求解得到了船舶预配载方案。Pacino 等［6］提出一种生成近似最优配载计划的两阶段方法，以最小化倒箱为目标，使用CPLEX 求解器求解混装策略下的主贝计划（MBPP）问题。Monaco等［7］研究了面向码头的船舶配载规划问题，以最小化集装箱运输时间和堆场移动次数为目标建立了二元整数模型，其设计的禁忌搜索算法能够在较短时间内找到近似最优解，但该模型忽略了堆栈的稳定性约束。Ambrosino等［8-9］将MBPP扩展为多港口主贝计划（MP-MBPP）问题，考虑了舱盖对配载的影响，以最小化船舶在港停泊时间为目标建立了新型混合整数规划模型，能够在较短时间内求解可容纳超大型船舶的配载计划。Li等［10］研究了集装箱班轮运输配载规划问题，以20 ft和40 ft普通箱为研究对象，通过基于启发式算法的贪婪随机自适应搜索算法求解MBPP问题。

以上对多港口主贝计划问题的研究很少考虑双40 ft岸桥装卸对配载的要求，且配载箱型较为单一，难以适应大型港口装卸设备更新换代的趋势。本文考虑双40 ft 岸桥装卸对配载的要求，以20 ft 和40 ft普通箱和冷藏箱为配载对象，以岸桥装卸次数（双40 ft岸桥适合率最高）与倒箱最小为总目标，考虑船舶稳性等限制构建多港口主贝计划配载模型，通过基于启发式规则的装箱算法验证可满足双40 ft岸桥装卸的配载策略，同时验证模型的有效性。

1 问题描述

集装箱船的多港口配载问题旨在为航线经营商指定的特定航线的集装箱船制订配载计划，其目标是满足服务需求并缩短船舶在各个港口的停留时间［11］。空船自初始港装载起航，途经各港口p，分别完成卸载当前目的港的集装箱组并装载一组带有目的港d属性的集装箱，行至最终港卸下所有集装箱。集装箱船的货舱以若干具有防漏结构的舱盖划分为甲板和舱内两部分，一块舱盖可覆盖其下几个相邻贝位。假设将某一舱盖的甲板和舱内位置都分配给一个目的地，采用此配载方式可以避免舱盖的多次抬放并提高装卸效率［12］。海船结构如图1 所示，一般使用连续的奇数01、03、05……表示船舶奇数贝，用奇数贝之间的偶数02、06、10……表示船舶偶数贝。

船舶配载时，首先需重点考虑双40 ft 岸桥对配载的要求，划分箱组时尽量保证可以满足双40 ft 岸桥常见满载装卸工况，发挥双40 ft 岸桥装卸优势。其次需尽量避免冷藏箱倒箱，且冷藏集装箱仅可堆存于安装有电源插头的特殊箱位，同时需考虑船舶全航线稳性［13］。

图1 船舶结构Fig.1 Ship structure

2 数学模型

基于以下假设建立MP-MBPP模型：

（1）航线各挂靠港中待装集装箱的属性信息已知，如集装箱的类型、尺寸、目的港、数量、质量等。

（2）集装箱船结构已知，包括船舶贝位数量、各贝容量、编号等信息。

（3）仅考虑20 ft 和40 ft 干货箱和冷藏箱，忽略超限箱和危险箱等。

2.1 集合

P为集装箱船航线经过的港口集合。

S 为集装箱尺寸集合，∀s∈S={1，2}，1 表示集装箱尺寸为20 ft，2表示集装箱尺寸为40 ft。

T 为集装箱类型集合，T={τ1，τ2}，τ1、τ2分别表示集装箱为普通干货箱和冷藏箱。

H 为船舶舱盖集合，H=HP∪HA=HL∪HR，其中HP为船舶船首舱盖集合，HA为船舶船尾舱盖集合，HL为船舶左舷舱盖集合，HR为船舶右舷舱盖集合。

Hpc为岸桥在p港服务的舱盖子集。

Q(p)为港口p的（o，d）对集合（o表示初始港，d表示目的港），Q(p)={a|o，p，d ∈P，a=(o，d)}。

2.2 参数

2.3 变量

xh，sτ(a)为在舱位h 装载的尺寸为s、箱型为τ 且满足初始港为o，目的港为d（即满足(o，d)对）的集装箱 数 量。xh，sτ(a)=x_hh，sτ(a)∪x_dh，sτ(a)，其中，x_hh，sτ(a)与x_dh，sτ(a)分别代表舱内与甲板上装载的尺寸为s、箱型为τ 且满足初始港为o，目的港为d的集装箱数量，a=(o，d)∈Q(p)。

y_hh，sτ(p)、y_dh，sτ(p)分别表示在港口p、舱内与甲板完成装卸后的集装箱量，是一个状态变量。

zh(p)为0—1变量，舱位h在p港不为空则为1，否则为0。

z_dh(p)、z_hh(p)为0—1变量，表示舱位h的甲板或舱内不为空则为1，否则为0。

rh，sτ(a)为在舱位h 产生的舱盖倒箱量（产生倒箱的舱盖之上的所有集装箱的数量）。

fp，h为如果发生舱盖倒箱，则为1，否则为0。

2.4 多目标优化模型

多目标优化模型如表1所示。

本文的优化目标分别为最小化航线内各港口倒箱量和最小化航线内各港口岸桥装卸次数，即满足双40 ft岸桥常见满载装卸工况的集装箱对最多。式（3）表示所有拟装船的集装箱均可装船。式（4）、（5）表示港口集装箱船的集装箱状态更新。式（6）～（8）限制了集装箱船的承重和容量。式（9）、（10）限制了船舶的稳性公差。式（11）表示当舱盖为空时，才可以装入相应舱盖的舱内，且待装箱量不大于舱内容量。式（12）～（14）限定了在何种情况下可以发生舱盖倒箱，并对倒箱总量加以限制。式（15）限制同一目的港至少相隔2个舱盖距离分配岸桥。式（16）使航线各港口双40 ft 岸桥的最大完工时间尽可能小，即满足双40 ft满载作业工况的配载箱尽量多。

MP-MBPP 属于三维装箱问题，是难以精确求解的NP（non-deterministic polynomial）难问题。为避免集装箱船配载方案搜寻空间大、耗时长，可以采用基于集装箱分组、排序的启发式算法［14］或构造算法［10］构造初始解，设计优化算法进一步提高初始解质量，以便在有效时间内获得较优解。结合研究对象NP 难特点，论文根据目的港、尺寸类型等属性将集装箱分组，按舱盖地址重新划分贝位，将MPMBPP转化为“集装箱箱组‒新贝位”装箱问题，通过挖掘贝位剩余容量等启发信息，设计启发式规则，有效解决考虑双40 ft 岸桥装卸的多箱型集装箱船的MP-MBPP。

由于同一箱组中的集装箱数量可能大于待装贝位容量，需要进一步拆分箱组，依次装载［5］，以解决物品尺寸超过箱子容量的超尺寸装箱问题。基于启发式规则的超尺寸装箱算法原理是当待装集装箱组大于当前港剩余容量最大的贝位，则按照剩余容量最大的贝位分割集装箱组，依次完成各拆分部分的装载。当待装箱组中的集装箱类型、尺寸存在差异时，不同的箱组分割策略将对配载结果产生较大影响。本文考虑贝位内是否混装20 ft与40 ft集装箱，提出船舶偶数贝（40 ft 贝）内20 ft 箱和40 ft 箱混装、20 ft 箱和40ft 箱不混装两种配载策略，具体配载策略如图2和图3所示。

表1 多目标优化模型Tab.1 Multi-objective optimization model

4 算例求解

4.1 案例参数

以船舱容量为1 696 TEU、舱盖数为10的海运集装箱船为例，验证算法的有效性。船舶贝位信息如表2所示［15］，船舶稳性相关参数纵倾力矩为437 383 800 N⋅m，横稳心距基线高度为12.68 m［14］。

船舶所经航线包含5 个港口，航次中具体的货运量如表3 所示，其中c 表示干货箱，rc 表示冷藏箱。

表2 船舶各贝位装载量Tab.2 Capacity of each bay of the ship

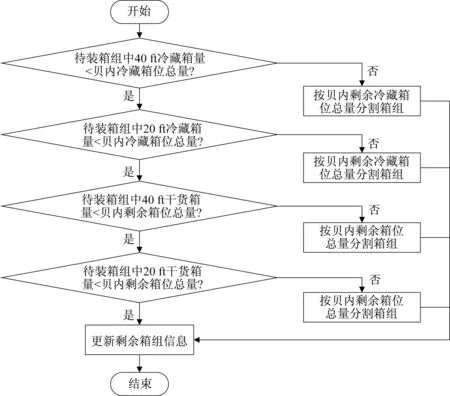
图2 贝内混装策略Fig.2 Mixed loading strategy in bay

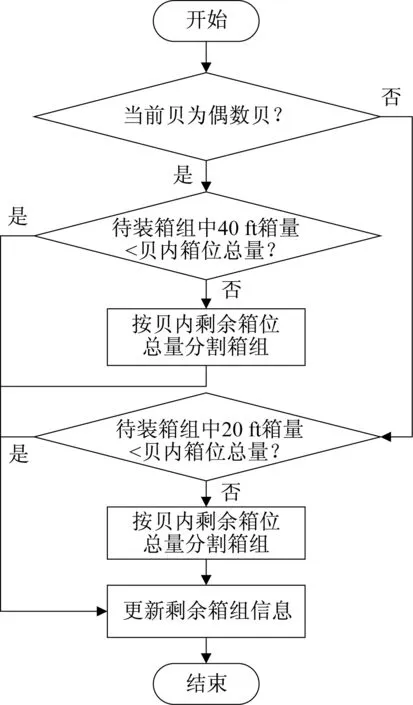
图3 贝内不混装策略Fig.3 Non-mixed loading strategy in bay

由于海船的装卸需要考虑舱盖的影响，现按照该船的10 个舱盖自艏至艉以01～11 的顺序进行编号，结合船舶结构与各贝容量，重新划分后的舱位容量信息如表4 所示，配载时将以舱盖所在舱位所覆盖的甲板和舱内的容量为单位进行集装箱组的装卸。其中，每个舱内容纳的冷藏箱位数分别是8、16、28、32、32、32、32、32、32、22、0。

4.2 结果分析

若不使用启发式规则，则难以在有效时间内获得船舶配载方案，加入此规则后，原问题最大计算规模由C6571694减少为C1622，大大加快了求解速度。实例的配载方案最优解不存在倒箱作业，船舶偶数贝（40 ft贝）内20 ft 箱和40 ft 箱混配、20 ft 箱和40 ft 箱不混配两种配载策略致使船舶贝位占用率不同，同时，两种策略下，双40 ft 岸桥满载作业次数及装卸完工时间亦有不同。

4.2.1 不同配载策略对结果的影响

为更好地表示不同策略对双40 ft岸桥的装卸效率的影响，引入对二者差值进行定量分析后的比值参数α，α =（贝内混装策略下双40 ft 岸桥装卸次数-贝内不混装策略下双40 ft 岸桥并行作业装卸次数）/ 贝内混装策略下双40 ft 岸桥装卸次数×100%，表示同等条件下，不混装策略相较于混装策略工作效率提升的程度。由表5 可以看出，岸桥数量充足时，不混装策略明显优于混装策略，最高可提升超过30%的效率。

图4 算法流程图Fig.4 Flowchart of algorithm

表3 船舶货运箱量Tab.3 Number of shipping containers

表4 舱位容量Tab.4 Hatch capacity

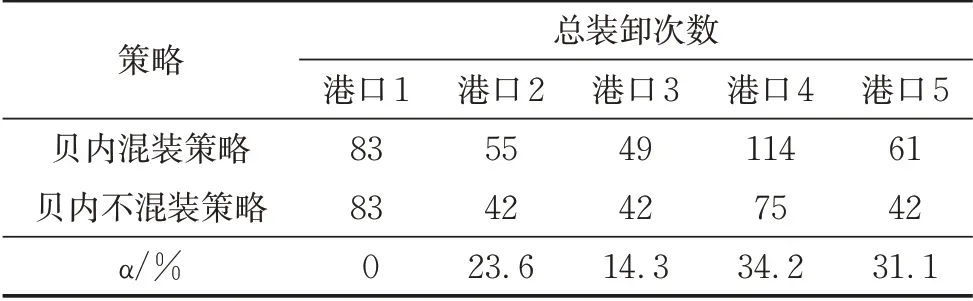
表5 双40 ft岸桥并行作业各港口总装卸次数Tab.5 Total loading and unloading times of twin-40-feet quay crane parallel operation at each port

图5、图6分别为各港口最多可以配备的双40 ft岸桥的数量与船舶贝位占用率，可以发现非混装策略下各港口最多可分配的双40 ft 岸桥数量相对更多，船舶贝位占用率也更高。

4.2.2 岸桥类型对结果的影响

普通岸桥在贝内不混装策略下相较于贝内混装策略提升的效率见表6，可以发现，普通岸桥与双40 ft岸桥呈现出相同的效率提升趋势。

图5 各挂靠港最多配备的双40 ft岸桥数Fig.5 Maximum number of twin-40-feet quay cranes in each port

为体现不同策略下双40 ft岸桥与普通岸桥相比可提升的装卸效率，引入对二者差值进行定量分析后的比值参数β，β=（普通岸桥并行作业各港口总装卸次数-双40 ft 岸桥并行作业各港口总装卸次数）/普通岸桥并行作业各港口总装卸次数×100%，表示同等条件下，双40 ft 岸桥较普通岸桥可提升的工作效率。

双40 ft岸桥较普通岸桥可提高的作业效率见图7。由图7可见，贝内不混装策略允许并行作业的岸桥数量更多且避免了频繁更换吊具，相比于贝内混装策略，能够在不同程度上提升更多的作业效率。

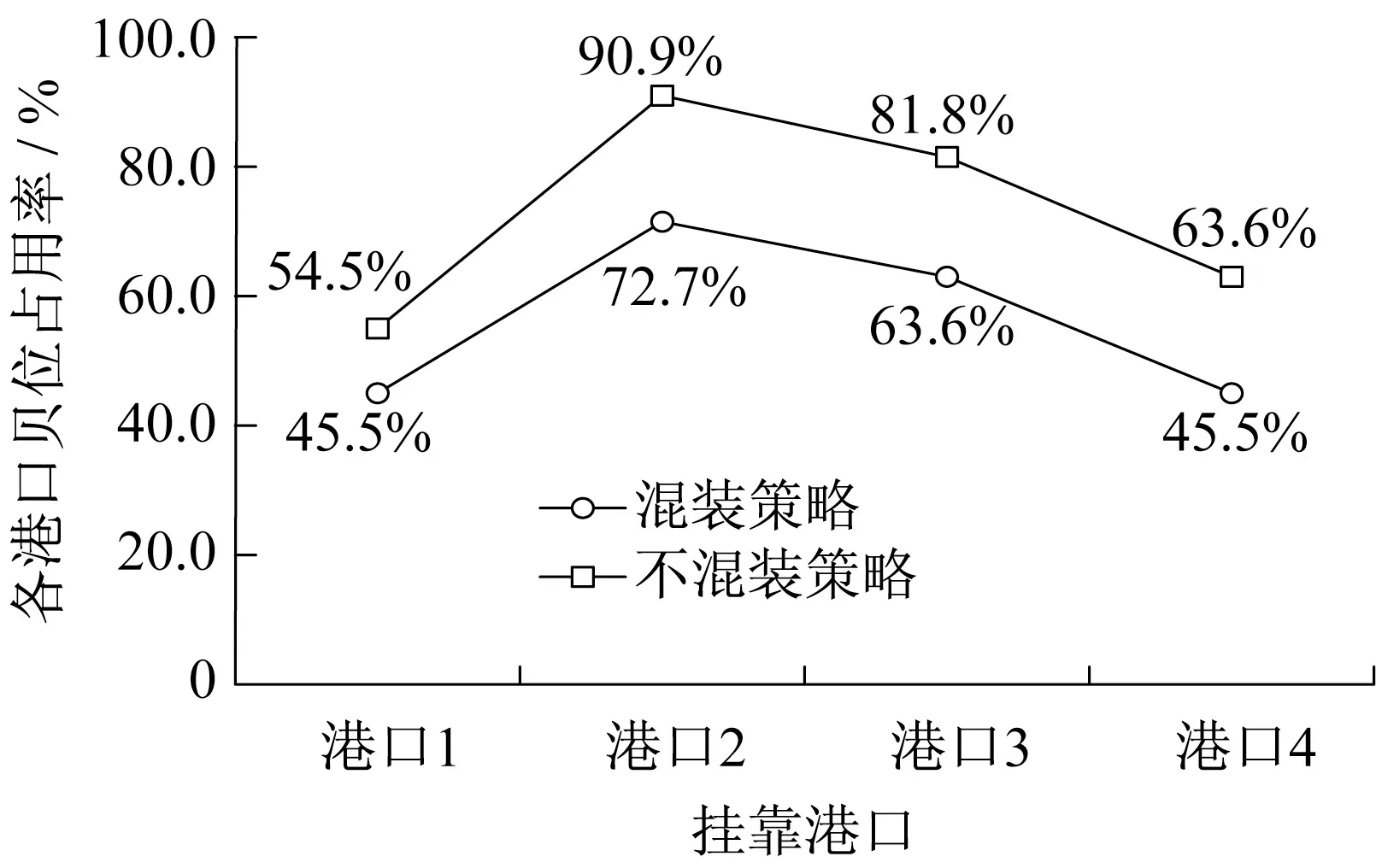
图6 贝位占用率Fig.6 Occupancy rate of bay

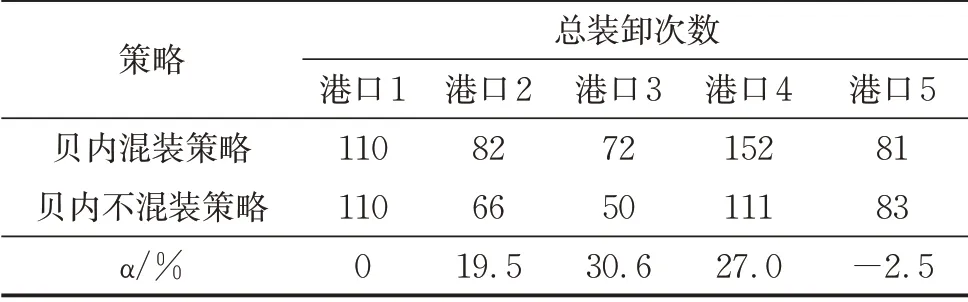
表6 普通岸桥可并行作业各港口总装卸次数Tab.6 Total loading and unloading times of common quay crane parallel operation at each port

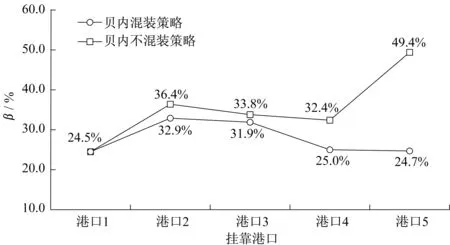
图7 双40 ft岸桥较普通岸桥效率提升比率Fig.7 Efficiency improvement ratio of twin-40-feet quay crane compared with common quay crane

5 结论

本文考虑双40 ft岸桥配备及船舶舱盖等对集装箱船航线的影响，以20 ft和40 ft干货箱和冷藏箱位作为配载箱型，以航线各港口装卸次数和舱盖倒箱最小为目标，以船舶稳性和容量等为约束，研究了考虑多港口双40 ft岸桥装卸的船舶主贝计划问题。提出了20 ft 与40 ft 集装箱混装和不混装两种装箱策略，利用多港口主贝计划模型设计了基于启发式规则的超尺寸装箱算法。结果表明，设计的模型和算法能够为实际算例提供有效的解决方案，主要有以下两个结论：

（1）在岸桥数量充足时，双40 ft岸桥在贝内不混装策略下的装卸效率明显优于贝内混装策略。

（2）配载模型和算法求解的配载方案能满足配备双40 ft 岸桥的需要，若配备双40 ft 岸桥进行装卸，同等条件下，较普通岸桥提升的比例在贝内不混装策略下呈现出更好的上升趋势。

作者贡献说明：

张艳伟：确定研究内容，修改文稿，确定文稿。

马佳乐：设计实验，整理结果数据，撰写文稿。