Evaluation method for helicopter maritime search and rescue response plan with uncertainty

Hu LIU, Zikun CHEN, Yongling TIAN,*, Bin WANG, Ho YANG,Gunghui WU,c

KEYWORDS Evaluation method;Maritime search and rescue;Probability distribution;Response plan;Robustness;Uncertainty factors

Abstract Helicopter plays an increasingly significant role in Maritime Search and Rescue(MSAR), and it will perform MSAR mission based on response plans when an accident occurs.Thus the rationality of response plan determines the success of MSAR mission to a large extent.However,with the impact of many uncertainty factors,it is difficult to evaluate response plans comprehensively before performing them. Aiming at these problems, an evaluation framework of helicopter MSAR response plan named UMAD is proposed in this paper, which reveals the influence mechanism of uncertainty factors based on Multi-Agent method and analyzes the mission flow based on Discrete Event System (DEVS) method. Furthermore, the evaluation criterion and indicators of response plan are extracted from the aspects of safety and effectiveness. Meanwhile, the Monte Carlo method is adapted to calculate the probability distribution and robustness of response plan comprehensive result. Finally, in order to illustrate the validity of this method, it is discussed and verified by an application example of evaluating multiple response plans to the same MSAR scenario. The results show that this method can analyze the influence of uncertainty more systematically and optimize response plans more comprehensively.

1. Introduction

With the increasing of maritime economic activity such as fishing, cruise travel and sea transportation, maritime accident occurs more and more frequently, an important insurance of which is the Maritime Search and Rescue (MSAR). When a series of accidents occur and cause casualties in a short time,it is important for the Search and Rescue Unit (SARU) to search the sea area quickly and rescue people in danger safely.The response plan and experiment of SARU Jointly determine the success of MSAR mission. Helicopter plays a crucial role in MSAR mission mainly because of its unique characteristics,such as low-altitude search ability,hovering rescue ability and quick response ability,which can make people out of danger in less time than other SARUs.

Therefore, this paper emphasis on the helicopter MSAR response plan. It belongs to the field of emergency management,and one of the core scientific issues is the evaluation theory and method of emergency response. Many domestic and international scholars have done a lot of research on this issue.

In order to solve the evaluation issue, the significant factor is the Evaluation Indicator System (EIS). Some important studies have been carried out on the EIS of emergency response evaluation. Zhang et al.,propose the EIS of maritime emergency capability, then it can be evaluated from five aspects including daily job, contingency plan and manoeuver,emergency rescue team and behavior, guarantee capability of resources and technical support. Jia et al.,suggests an EIS construction method of emergency capability, which is based on the four-layers weighted super network model and the indicator importance sort algorithm. Hao et al.,propose a fourlevel EIS focused on maritime emergency management, and evaluate its capability using the analytic hierarchy process and fuzzy comprehensive evaluation model. However, these study are mainly oriented towards maritime emergency response capability, not the maritime emergency response plan.

In addition,one of the inevitable problem for response plan evaluation is uncertainty, because of the varied environmental factors and the evolving accident situation.Many studies have been carried out on the uncertainty of emergency response evaluation, with the same emphasis on maritime emergency capability. Xu et al.,aiming at the fuzziness and randomness in evaluation problem of maritime emergency capability, propose a simulation evaluation method based on cloud model,and show that the evaluation result provides more information than the traditional fuzzy comprehensive evaluation method.Zhang et al.,aiming at the fuzziness and randomness in evaluation problem of maritime emergency management capability, propose a novel grey cloud clustering comprehensive evaluation model, which is applied to evaluate Guangzhou maritime emergency management capability, and it can help decision makers to improve their accuracy. On this issue,researchers also focus more on the aspect of capability.

When it comes to emergency plan, some key issues have been studied.Xu and Nieanalyzes the key distinction between emergency contingency plan and response plan. they illustrate that the former is to clarify the important responsibilities and working process mainly from the perspective of emergency management, while the latter is to solve specific emergency mainly from the perspective of emergency technology. In another words, the former emphasizes on who should do,and the latter emphasizes on how to do. Huang,aiming at the uncertainty problem in the emergency contingency plan evaluation, proposes a simulation & demonstration platform of emergency contingency plan.And the main functions in this platform consists of establishing EIS, simulating emergency response process and integrating a variety of different information.

The emergency response evaluation result is only meaningful if it can be applied in practice.There are lots of application researches worthy of reference.Jacobsen and Gudmestad,discuss the feasibility of providing long-range search and rescue in the Barents Sea,then proposes a method to provide enough search and rescue capability,which covers within a distance of 260 nautical miles and can save at least 21 persons within two hours. Ju et al.,highlight that one of the major subjects in emergency management science is to evaluate and select the most desirable emergency alternative. This problem is solved in 3 stages,firstly obtaining the relation among evaluation criteria or sub-criteria for alternatives, secondly calculating the global weight of indicators, and finally ranking the emergency alternative.

It can be seen form the abve description that the current researches on MSAR evaluation problem mainly concentrates on emergency capability,but studies about response plan is relatively few. What is more, it is necessary to consider the influence of uncertainty factors in the evaluation process of helicopter MSAR response plan, because of the unknowable outcome after executive process. And the analysis of the evaluation results is also necessary.

Aiming at these problems mentioned above, an evaluation framework of response plan named UMAD is proposed in this paper. Then through sufficiently analyzing uncertainty factors and mission flow, the EIS of response plan is extracted. After that the calculation method of indicators is determined, by which the probability distribution and robustness of response plan comprehensive result can be obtained. On this basis, a simulation&evaluation prototype system has been developed,then the validity of evaluation method is illustrated by using this system to evaluate different response plans of a same helicopter MSAR mission scenario. The evaluation results show that this method can be used to evaluate the helicopter MSAR response plan more comprehensively.

2. Evaluation framework

2.1. Response plan and uncertainty factors

Response plan is very important in the helicopter MSAR mission, it is not only the communication bridge between commanders and performers, but also the important basis for helicopter to perform MSAR mission. Compared with Land Search and Rescue (LSAR), the MSAR is more affected by uncertainty factors, and these influences will appear in all stages of emergency response, Fig. 1 shows the state of helicopter rescuing the boat in distress.Therefore,before carrying out the research content of this paper in detail, it is necessary to explain the definition of the response plan and the uncertainty factors.

Fig. 1 Helicopter maritime search and rescue.

2.1.1. Definition of response plan

Based on the previous researches,the MSAR response plan for SARU mainly includes two parts, the SARU matching and the SARU action.So it can be represented by a binary group.

The SARU matching Mmeans assigning a specific action to an SARU. If n is the number of actions required to complete this mission, m is the number of SARUs, then it can be represented by the following matrix.

The SARU action Arefers to the specific actions matched by an SARU.If the number of actions that iSARU has been matched is n, then it can be represented by the following formula.

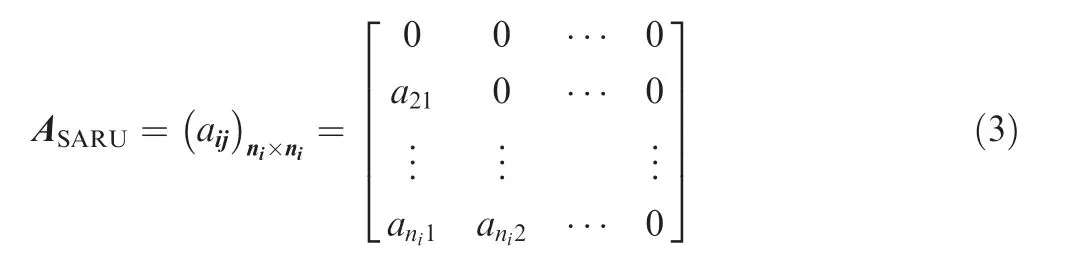
where a=0，1 and a=1 means the jaction will be executed before the iaction.

This study focuses on the common MSAR mission pattern that single-helicopter-single-flight search and rescue distress ship. According to the response plan of actual MSAR flight service team,the RPmodel can be simplified into the following formula.

where saru*is the helicopter that will perform this mission,Ais the specific actions in navigation stage represented by the waypoints from base to mission area, Ais the specific actions in search stage represented by the range of mission area and search pattern, Ais the specific actions in rescue stage represented by the method to rescue the distress people, Ais the specific actions of evacuation stage represented by the waypoints from mission area to base. It is worth mentioning that the definition of these four stages will be defined and analyzed in the following parts.

2.1.2. Uncertainty factors

In the specific helicopter MSAR mission pattern, there are many Uncertainty Factors (UFs) can influence the effectiveness of response plan, which mainly include the uncertainty of ship drift uf, the uncertainty of ship status uf, the uncertainty of SARU detecting to ship uf,and the environment uncertainty uf. In order to facilitate the establishment of follow-up methodology, these UFs must be further analyzed, which are described as follow.

When a ship loses power at sea,its position will be changed with the influence of surface wind and current field. However,the drift trajectory is uncertain according to the calculation method of wind-driven drift and current-driven drift,which are related to immersion ratio and ballast condition.When a ship is in danger at sea, it will experience many statuses such as tilting,turning over,sinking,because of its internal and external factors, but the transition time between statuses is uncertain. When a helicopter fly over the distress ship, the detection probability is subject to a distribution with relative distance,cruising speed and visibility.This distribution is usually a dynamic value,and must be real-timely calculated.Many marine environment uncertainties can directly impact the helicopter and distress ship, such as surface wind and current field, wave height, temperature, and so on.

It can be seen that the UFs will influence the helicopter MSAR mission immediately, and then further affect the effectiveness of response plan. Therefore, the relationship between effectiveness and UFs can be eventually expressed as a highly nonlinear relationship, which is shown in Eq. (5).

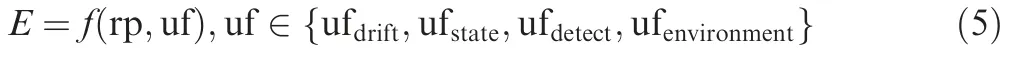
where E means the effectiveness,f means the helicopter MSAR mission, rp means the response plan, uf means the UFs.

2.2. Framework of UMAD

Response plan is developed for the helicopter based on MSAR mission,and limits the actions to be taken by helicopter during each mission stage. However, the helicopter will interact with distress ship when performing the response plan. According to the analysis of UFs,both helicopters and distress ships have their own internal UFs, which will be not only influenced by each other, but also affected by the UFs in the environment.As a result, the UFs can be seen as an interactive medium among helicopter, distress ship and environment. Based on the above analysis,the UMAD framework for evaluating helicopter MSAR response plan has been proposed, which is shown in Fig. 2.

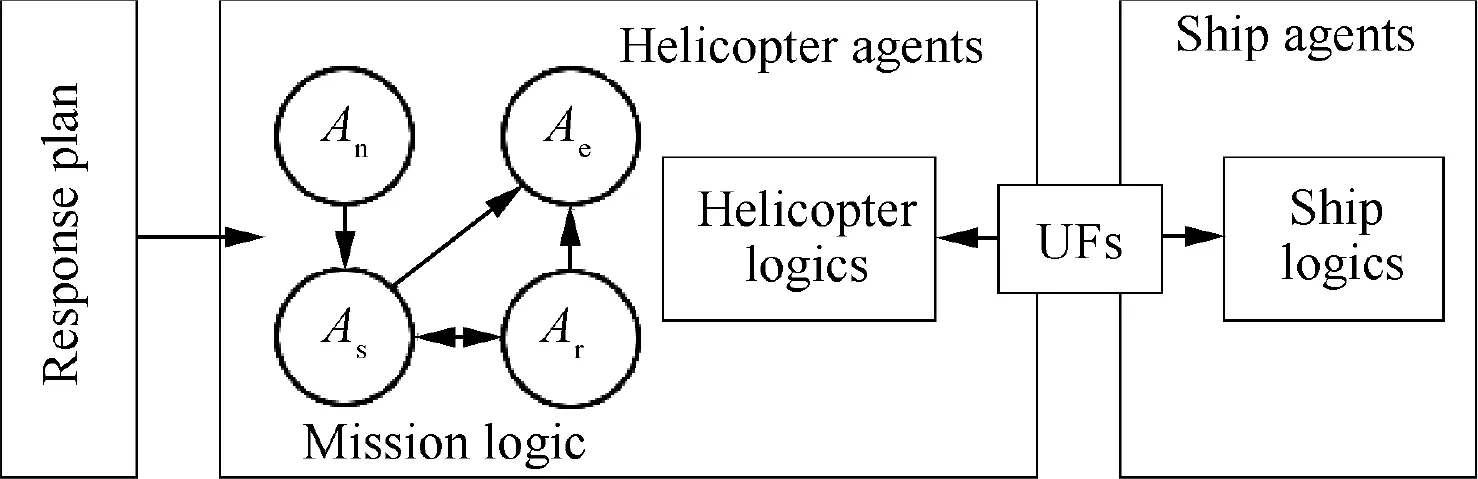
Fig. 2 Framework of UMAD.

This framework establishes agent models of helicopter and distress ship based on Multi-Agent method,and the interactive relationship between them is established through UFs.And then the mission flow of helicopter MSAR response plan is modeled based on DEVS method,which provides theoretical and methodological support for subsequent evaluation procedure. The specific modeling process will be described in detail in the following parts.

2.2.1. Multi-agent model considering UFs

It can be seen from the helicopter actual MSAR process that solving the modeling problem of helicopter and distress ship is of significance.For the helicopter,the main modeling efforts consist of the movement logic in performing mission and the detection logic in searching target. The former needs to be modeled according to the standard operating procedure of helicopter MSAR,while the latter needs to establish the detection model of helicopters to distress ships. For the distress ship, the maritime drift logic and state evolution logic must be mainly analyzed.The former needs to be modeled according to the drift trajectory obtained by prediction algorithm, while the latter needs to be modeled according to the change of environment and the performance of helicopter. It can be seen from the above analysis that the helicopter model and distress ship model have their own logic and influence each other.According to the methodology of Non-Uniform Hybrid Strategy(NUHYS),these two models can be established based on Agent-Based Modeling (ABM) method, which will guarantee the model accuracy and computational efficiency to a certain extent,then improve the authenticity of the evaluation results.Based on the above analysis,it can be seen that the logics in helicopter and distress ship agents contain the influence of uncertain factors, and it is the influence that closely connects these two agents. So the multi-agent model can be expressed as shown in Fig. 3. The dotted arrows represent the influence relationship between logics and UFs,and the solid arrows represent the internal relationship among UFs. This model illustrates the simulation logic of helicopter and distress ship,and the interaction between these two agents is revealed by the influence among UFs, which is expressed in the grey rectangle. At the same time, it should be pointed out that the multi-agent model can also support the MSAR mission flow analysis of multiple helicopters and multiple distress ships.

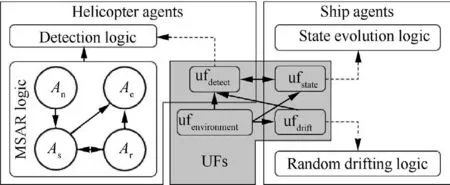
Fig. 3 Multi-Agent model considering UFs.

2.2.2. DEVS model considering UFs

The mission flow of helicopter MSAR is very complex because of many UFs, it contains not only many independent mission stages, but also many decision points needed to be judged.Besides the maritime accident has the characteristics of randomness and suddenness, as a result, the mission flow cannot be analyzed by pure mathematical method.Luckily,this problem can be solved by the DEVS methodwhich is proposed by Zeigler.

According to the structure DEVS model, it can be simply described as ‘‘event-active-event”. In order to build mission model more accurately, it is necessary to have a complete understanding of the mission flow and analyze the key information which can be used to model. According to the modeling theory of DEVS and the characteristics of MSAR, the events and activities in the mission model of helicopter MSAR are shown in Table 1, and the detailed mission flow considering UFs can be expressed as Fig. 4.

By analyzing the discrete ‘‘event-active” in DEVS model,and the close interrelationship between events and activities,the above mission flow can be divided into 6 main stages.They are information receiving A,decision making A,navigation process A, searching process A, rescuing process A, evacuation process A. Considering that the response plan is developed at the decision making stage and used to guide the performance of next 4 stages, a simplified DEVS model of the helicopter MSAR mission flow can be obtained, which is shown in Fig. 5.

It can be seen that the mission flow of helicopter MSAR mainly includes 3 stages. The first stage is information receiving, in which a large amount of useful information must be captured and filtered. For distress ship, the distress location,distress time,number of distress people,wind field and current field must be obtained. While for helicopter, its base location and MSAR performance should be obtained.The second stageis decision making, in which the drift trajectory and range of distress ship must be predicted firstly based on available information. And then the corresponding response plan can be developed after determining the MSAR mission area.The last stage is mission performing, in which the most suitable helicopter will perform MSAR mission according to the response plan. This stage occupies the majority of helicopter MSAR mission, and is mainly influenced by UFs, so it is the key part needed to be analyzed when evaluating response plan.In addition, what needs illustration is that the Aand Aexpress the round process to base and mission area, and the helicopter generally moves at fixed speed and altitude. So the last stage can be divided into three parts,which are search,rescue,transport sub-stages, so that it is convenient to facilitate the establishment of follow-up EIS.

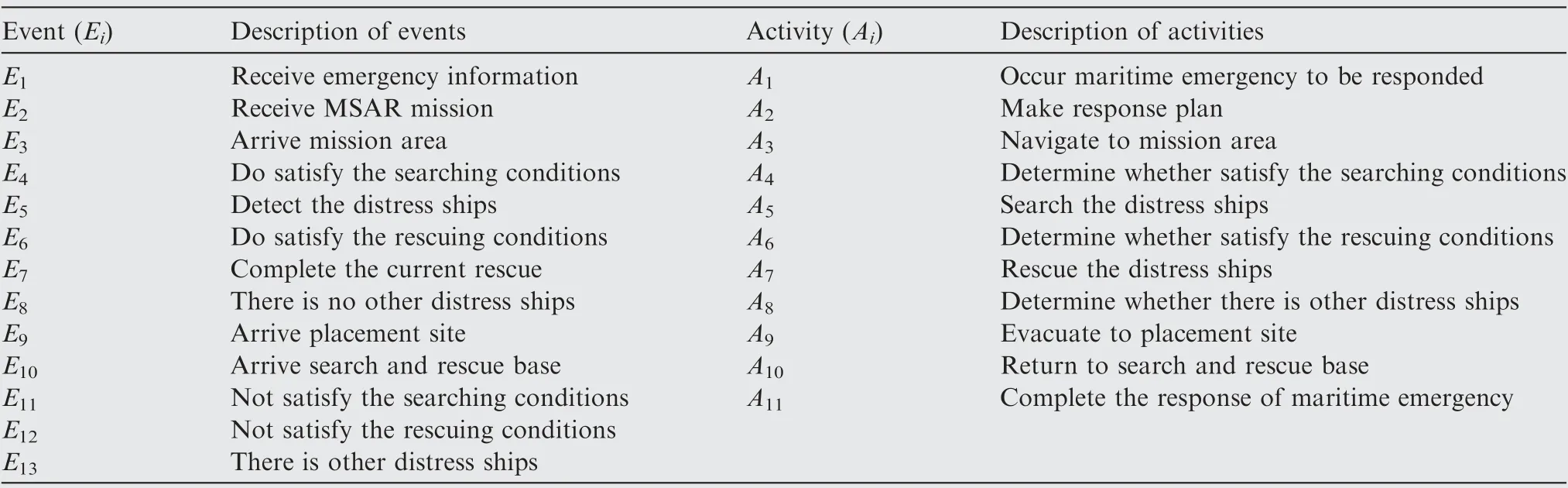
Table 1 Events and activities in helicopter MSAR mission flow.

Fig. 4 DEVS model of helicopter MSAR mission flow considering UFs.

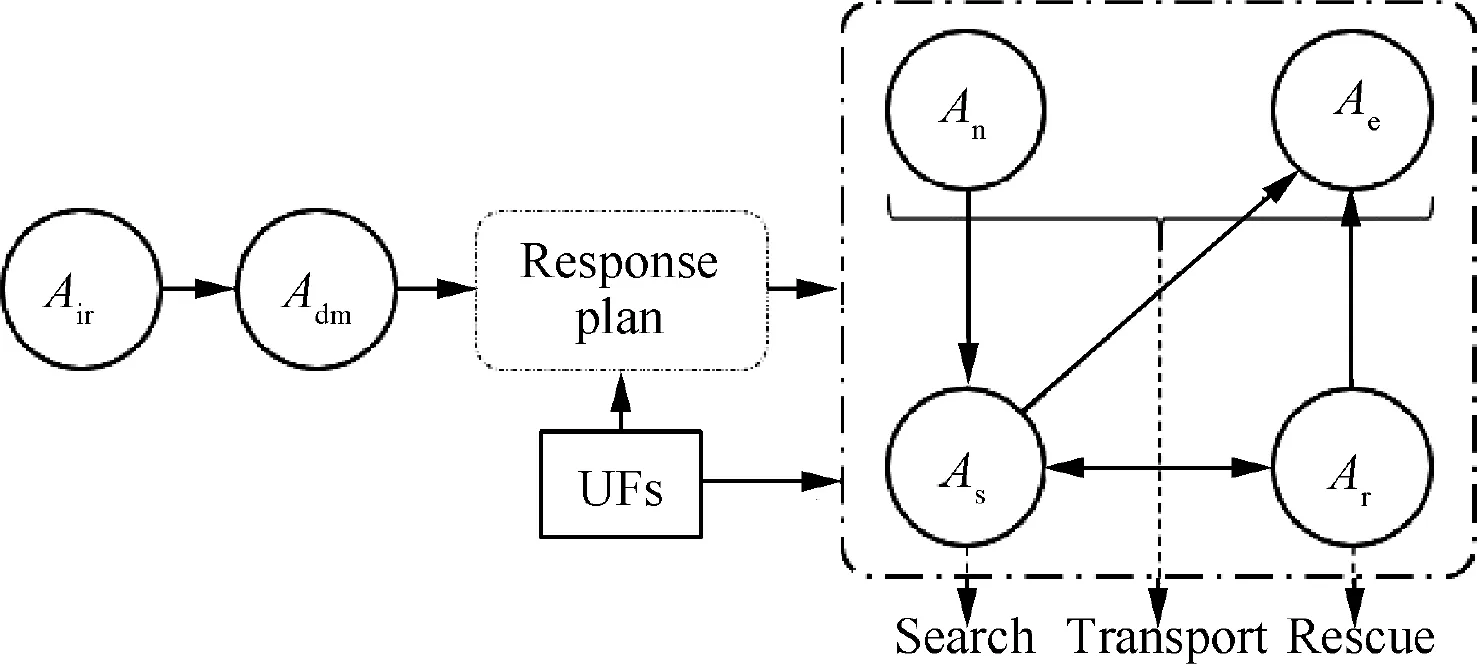
Fig. 5 Simplified mission flow.

3. Evaluation procedure

3.1. EIS for response plan

The evaluation of helicopter MSAR response plan is essentially a multi-criteria comprehensive evaluation problem, an important prerequisite of which is to build a reasonable EIS.According to relevant studies,the two aspects of safety and efficiency should be considered when evaluating and screening response plans.The main evaluation criteria includes the safety of SARU,the safety of distress target,search effectiveness,rescue effectiveness and time cost.

However, the time cost criterion reflects the overall efficiency in whole process of response plan execution, and the part of which has been reflected by the search efficiency and rescue efficiency.It can be seen that the efficiency of transport sub-stage has not been considered separately according to the simplified mission flow.For this reason,the time cost criterion is adjusted to the transport efficiency criterion.In this way,the coupling degree between evaluative criteria can be reduced as much as possible, which helps to extract evaluation indicators of response plan more accurately.

In view of the above considerations, the evaluation of helicopter MSAR response plan is mainly carried out from five aspects, namely helicopter safety C, distress ship safety C,search efficiency C, rescue efficiency C, and transport efficiency C. Cmeans that the safety degree of helicopter and its corresponding indicators must be extracted based on the factors which will influence the degree. Chas a similar meaning, but the focus is distress ship, so the indicators should be extracted considering the process from raising alarm to being rescued. According to the simplified mission flow, the mission performing stage includes three sub-stages.Therefore,the indicators of C, C, Cshould be extracted one-to-one corresponding with these sub-stages.

3.2. Subjective weight

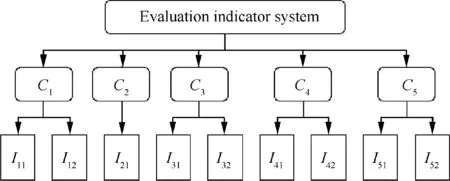
Fig. 6 EIS for helicopter MSAR response plan.

Due to the influence among UFs, the evaluation indicators of response plan will have mutual influence,so they are not independent with each other. By comparing AHP method and ANP method,it is found that the latter is more suitable for determining the weight of EIS for response plan. An ANP model is divided into two parts. The first part is the control layer made up of two basic elements, which includes an evaluation target layer and many evaluation criterion layers.In this part, each criterion is considered to be independent, not affected by other criteria,but at the mercy of evaluation target.The second part is the network layer, which consists of many indicators from the corresponding criterion layer in the control layer. These indicators form multiple clusters, which influence each other. To determine the weight of EIS based on ANP method is mainly carried out from the following aspects.

3.2.1. Building expert belief map

The ANP model is a group decision making process.But there are certain differences among experts in the judgement to same problem, and to obtain credible weight needs as many experts as possible. In order to improve the accuracy of weights, the expert belief map shown in Fig. 7 is adapted in this paper to analyze the judgement,which will further reduce the difference of different experts.

Fig. 7 Expert belief map.

3.2.2. Constructing the interrelation matrix

The interrelation matrix of indicators is used to determine the mutual influence relationship between indicators, and each expert makes a separate judgment on it, which can be expressed as follows.

3.2.3. Constructing the judgement matrix of indicators

The judgment matrix is used to compare the relative importance of indicators. According to the judgment requirements,this paper adopts the 9-level evaluation method to construct it. It is assumed that there are k experts evaluate the relative importance of Nindicators, the constructed judgement matrix can be expressed as follows.

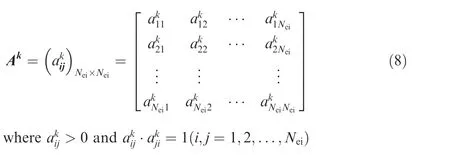
3.2.4. Integrating the opinions of experts

Because of the different authority and experience of experts,the interrelation matrix and judgement matrix of different experts are different as well.Therefore,they must be integrated based on the judgement weight of each expert, then the final interrelation matrix Rand the final judgement matrix Aare expressed as follows.

It can be seen that the ANP method mainly estimates the weight of EIS for helicopter MSAR response plan by analyzing experts’judgment results on the correlation among indicators.So this weight is the subjective weight.However,due to the influence of UFs,it is not sufficient to express the weight of EIS only by subjective weight.In this paper,entropy weight is adapt to calculate the objective weight of it,which will be analyzed in the next part.

3.3. Evaluation value and objective weight

There are many methods to analyze the mission performance stage of response plan,however,it can be seen by comparison that high efficiency and cost ratio can be obtained by simulation. Meanwhile, the evaluation result calculated by single simulation cannot fully demonstrate the effectiveness,because of the coupling effect of UFs. With these concerns,response plan must be comprehensively evaluated by analyzing a large number of performance processes.So the Monte Carlo simulationis adapted in this paper to calculate the value of indicators. In this way, not only more scenarios can be simulated to analyze different response plan, but also the influence of UFs can be more easily considered and a large number of experimental data can be obtained.

3.3.1. Calculation of indicator value

It is assumed that there were Nsimulation experiments,then the indicator simulation output matrix is expressed as follows.

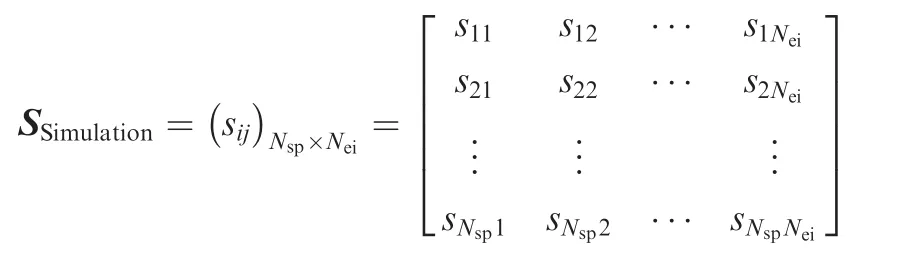
In the matrix S, the elements in each row represent the Nindicator value generated by the same simulation,and the elements in each column represent the different results of the same indicator.However,the original value cannot represent the evaluation results, so they need to be standardized based on marking criterion.

Based on the evaluation requirements of different indicators, the standardization process of original data mainly has two types.One of them is that there is a reference value for this indicator,and it is necessary to compare the original data with reference value during scoring.The other one is that there is a maximum value for this indicator,and the ratio of the original data to the maximum value needs to be calculated in scoring.

For the former type, the threshold method is adapted to complete the standardized processing. According to the relationship between original data and threshold value, this method can be divided into two conditions.

When the effective evaluation result of indicator is obtained in the case that the original data is bigger than the threshold value, the normalization method can be expressed as Eq. (11).

For the latter type, the standardized evaluation value will be calculated by the ratio of the original data to the maximum value, which can be expressed as Eq. (13).

3.3.2. Calculation of objective weight

The theory of information entropyis adopted to analyze the impact between UFs and weight of EIS, which represents the objective weight. There are two main reasons for this approach, the first one is the addition of UFs in the process of obtaining indicator simulation values, and the other one is the highly nonlinear relationship between UFs and indicators.

Entropy weight is the measure of influence degree between UFs and indicator simulation result in each response plan.And this measure does not change with the subjective will of experts. So entropy weight can be considered as the objective weight of EIS.

3.4. Representation of evaluation result

With the analysis of above two sections,the subjective weights and objective weights of EIS have been obtained, then the comprehensive weight can be obtained as follows.

where α is the fitting coefficient, μ is the mean value, σ is the standard deviation.

Because each simulation is equivalent to an independent sampling experiment from the same probability distribution.So the mean value of all simulations will be approximately equal to the expectation of this distribution when the sample size is large enough. Therefore, based on the robustness measurement method of Taguchi,the robustness of evaluation result can be expressed as the standard deviation of final evaluation result.

It is worth to be referenced, in the research of combat action plan,an effective way to deal with the battlefield uncertainties is to improve the robustness of it. Therefore, the measurement of robustness is the key to evaluate plans.Meanwhile, the helicopter MSAR response plan could be regarded as a kind of combat action plan, when it comes to dealing with the maritime accidents. Therefore, the system robustness measurement method proposed by Taguchi had been adapted in this paper, which considered the controllable χ and uncontrolled η input parameters. This method used the Mean Standard Deviation (MSD) to represent the deviation between the simulation results f(χ，η ) and the expected output μ. In this paper, the response plan is controllable parameter,and the uncertainty factor is uncontrollable parameter, then the MSD is shown as follows.

In order to compare the robustness of different response plans, the concept of Signal-to-Noise Ratio (SNR,SNR=-10log(MSD)) is further used to calculate the robustness of each response plan. So the larger value of SNR means that the robustness of response plan is stronger.

4. Framework of simulation evaluation system

Further analysis of UMAD method shows that it is necessary to obtain the contents of information receiving stage and decision making stage before developing the helicopter MSAR response plan. Then the response plan can be simulated through Monte Carlo simulation. In addition, according to the evaluation procedure of response plan indicators, the subjective weight and objective weight of EIS must be considered at the same time. And the objective weight can be obtained through simulation result of indicators.After that,the comprehensive weight and result of response plan can be calculated,which can be used to compare and select the optimal one.

In order to completely illustrate the evaluation procedure above, the simulation evaluation system framework of helicopter MSAR response plan has been designed in this paper,which is shown in Fig. 8. This framework consists of four parts, scenario editing module, decision making module,Monte Carlo simulation module and comprehensive evaluation module.In scenario editing module,it is necessary to edit the basic information of helicopter and distress ship.Then the drift trajectory of distress ship will be predicted in decision making module. Based on this, the MSAR mission area can be confirmed and the response plan can be developed. The Monte Carlo simulation module mainly contains the simulation logic of mission flow on the basis of UMAD framework.The last module illustrates the calculation procedure of response plan evaluation results.

Take this framework as a basis, the AnyLogic simulation software has been chosen in this paper to establish the simulation evaluation prototype system. And the organizational structure of prototype system is shown in Fig.9.The blue rectangles represent the main operating process of decision-maker,including scenario editing module, decision making module and comprehensive evaluation module, which are shown in Figs. 10-12. Meanwhile, the Monte Carlo Simulation Module has been modeled according to the UMAD framework, while the comprehensive evaluation module processes the large sample data based on the evaluation procedure.Fig. 11.

In scenario editing module, the information about emergency and SARU can be edited. The former is mainly used for the drift prediction calculation, the latter is mainly used for the response plan making.

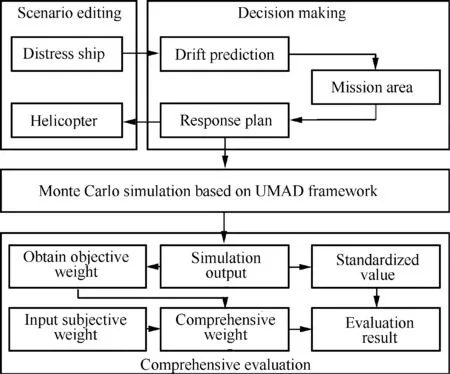
Fig. 8 Framework of simulation evaluation system.

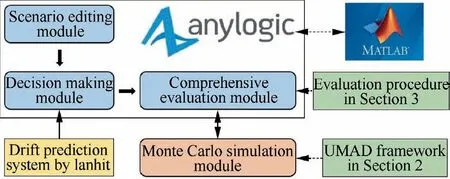
Fig. 9 Organizational structure of prototype system.

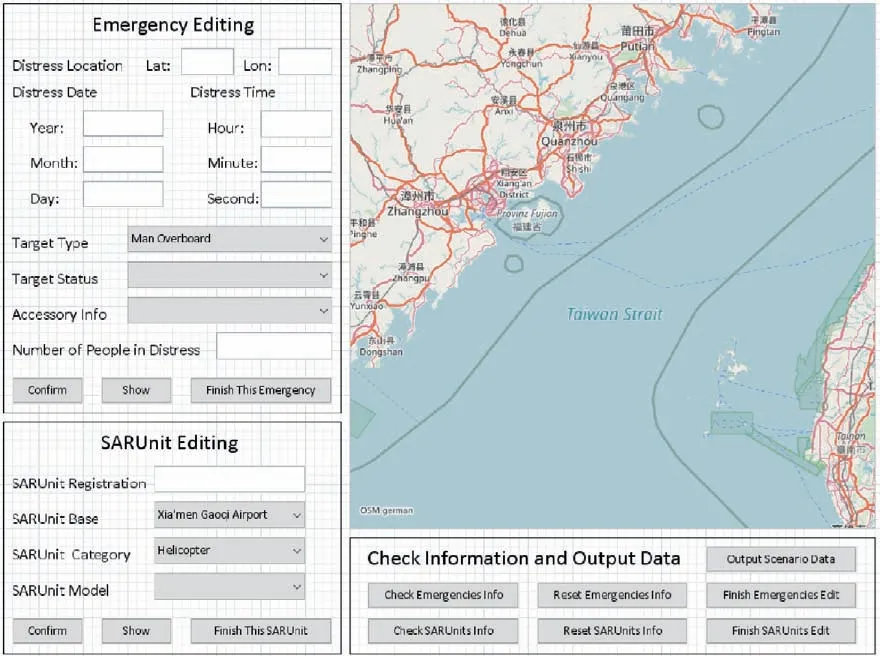
Fig. 10 Scenario editing module.

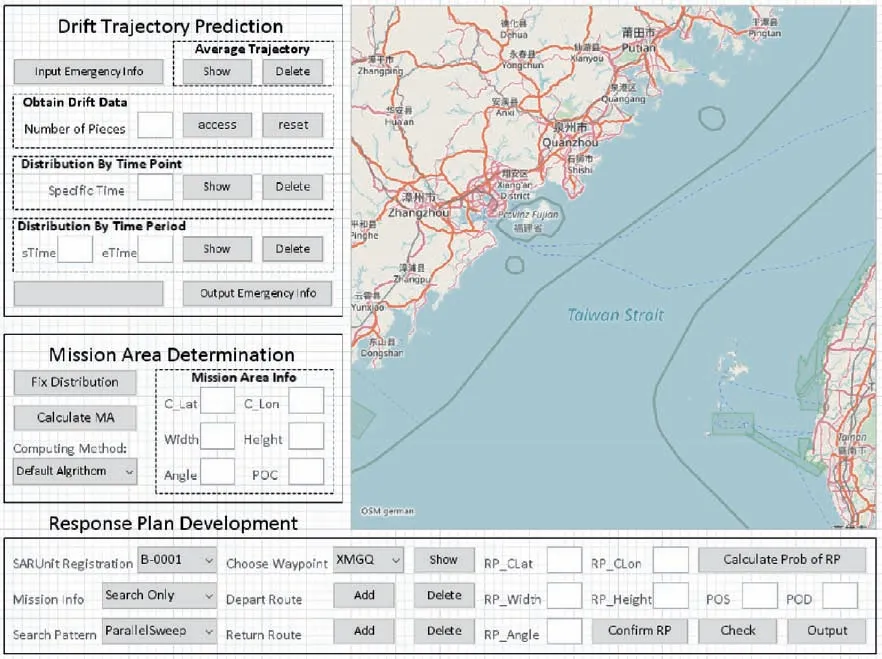
Fig. 11 Decision making module.

In decision making module,the drift prediction data can be obtained by the drift prediction system. The mission area of helicopter MSAR response plan can not only be calculated automatically based on the drift prediction data, but also be input by decision-maker. Then the drift prediction data and response plan will be output for the comprehensive evaluation module and the Monte Carlo simulation module.

In comprehensive evaluation module,the number of Monte Carlo simulation can be set and the evaluation procedure can be monitored. In addition, the subjective weight can be obtained by the method mentioned in Section 3.2, while the objective weight can be obtained by the method mentioned in Section 3.3, then the comprehensive weight will be calculated with Eq.(16).The 9 graphs at the top right show the evaluation values of the evaluation indicators in Table 2. And the larger figure below shows the comprehensive result of this response plan, which is calculated by Eq. (17). The rectangle at the lower right shows the data processing of original evaluation results,the fitting curve can be obtained according to Eq.(18), and the SNR value can be calculated according to Eq.(19).

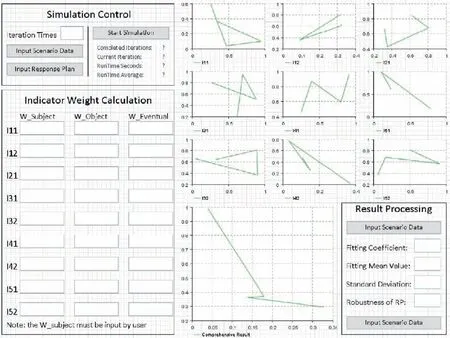
Fig. 12 Comprehensive evaluation module.

The process of Monte Carlo simulation is based on super real-time simulation, so it does not need to be manipulated by the decision-maker. However, its simulation results can be recorded by the comprehensive evaluation module for data processing.The operation logic of helicopter is very important in this simulation, which determines the final data output.Therefore, it is designed in detail according to Fig. 4, and the specific logic is shown in Fig. 13.

5. Case study

This paper takes an assumptive helicopter MSAR mission in East China Sea as an example with the consideration of all UFs mentioned in Section 2.1.2.First of all,the basic informa-tion of distress ship and response plans have been described.Then the subjective weight is calculated by ANP model, furthermore the indicator value and objective weight are calculated by simulation. After reviewing above, the comprehensive evaluation results of response plans will be obtained, which can be used to compare and screen the optimal plan.

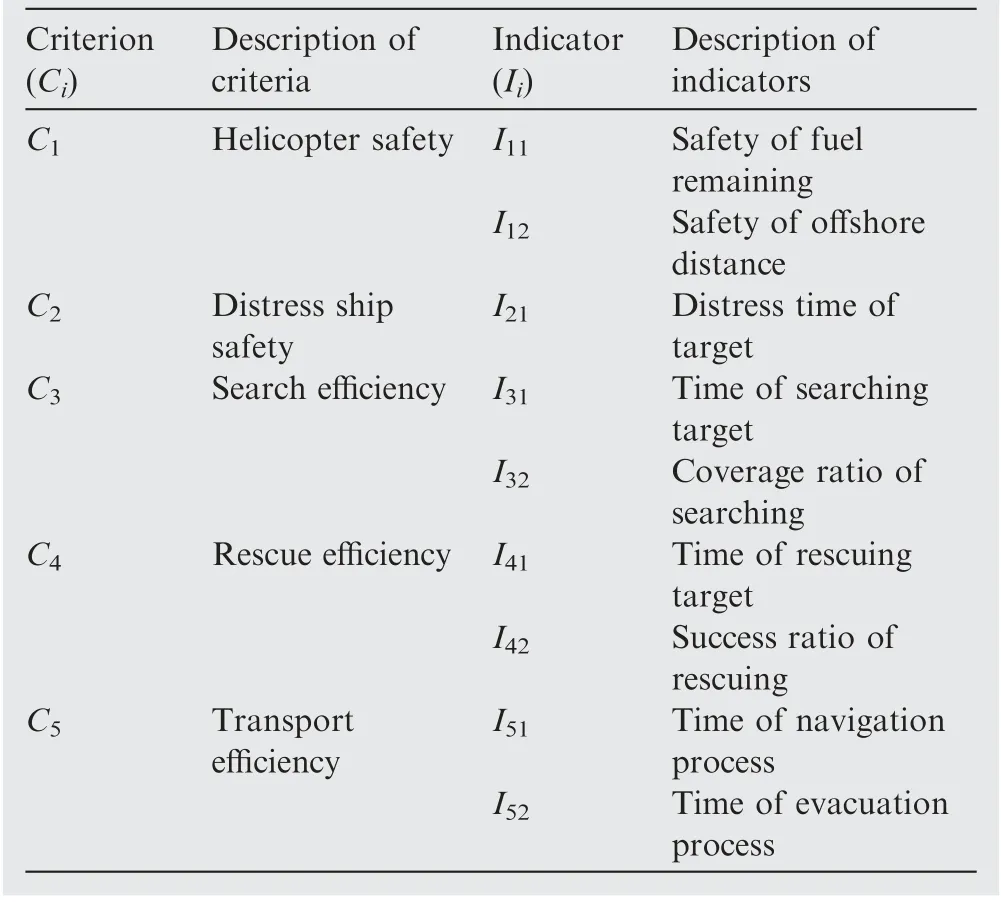
Table 2 Corresponding relationship between criteria and indicators.

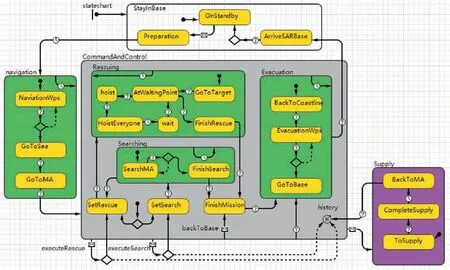
Fig. 13 Operation logic of helicopter.

Table 3 Basic information of maritime accident.

5.1. Expression of distress ship and response plan

5.1.1. Distress ship

When a ship is in distress, the information can be obtained through alarm systems,including the time of distress,position of distress, target type, target status and so on. So the basic information of distress ship is shown in Table 3.

5.1.2. Response plan

According to the requirements of civil aviation management,the route that helicopter fly off the coast from the same search and rescue base is relatively fixed. When the helicopter leaves the coastline, it will fly to the mission area in a straight line.Therefore, the difference among helicopter MSAR response plans is mainly reflected in the searching process.

In addition, because of the fast flight speed of helicopter,the time from receiving alarm to arriving mission area is usually very short. Under this specific circumstances, the drifting distance of the distress ship is also very short. So the point datum Search Pattern(SP)can be adopted,which mainly contains two SPs, the Expanding Square (ES) and the Polygon Sector (PS).

As a result,the mission area can be represented by Latitude(Lat) and Longitude (Lon) of its center and the Radius (R) of area.Then the four helicopter MSAR response plans are developed as shown in Table 4.

There are many key points must be explained:(1)B-0001 is a helicopter for MSAR in the simulation system, and it is deployed at Xiamen Gaoqi airport. (2) Pexpresses the waypoint of sailing route for transform process. The P, P, P,Pmean the sailing route for navigation process, while the P, P, P, Pmean the sailing route for evacuation process.(3) The waypoints of helicopter in mission area will be calculated automatically by simulation system according to Lat,Lon,R and SP.(4)The rescue pattern is related to SARU type,helicopter generally uses hover rescue pattern.And the specific procedure will be simulated in system.

The schematic diagram of response plans in system interface are shown in Fig. 14, where the solid red line is the planned flight path of helicopter, and the yellow dot set is the predicted drift trajectory of the distress ship. According to the optimal search theory created by Koopman,the optimal MSAR mission area can be calculated in the case that the drift trajectory prediction results are obtained. However,since this study only focuses on the evaluation problem of response plan, the optimized analysis of mission area in it will not be considered for the time being. This new problembelongs to the decision making issue for response plan, which will be carried out in the follow research.

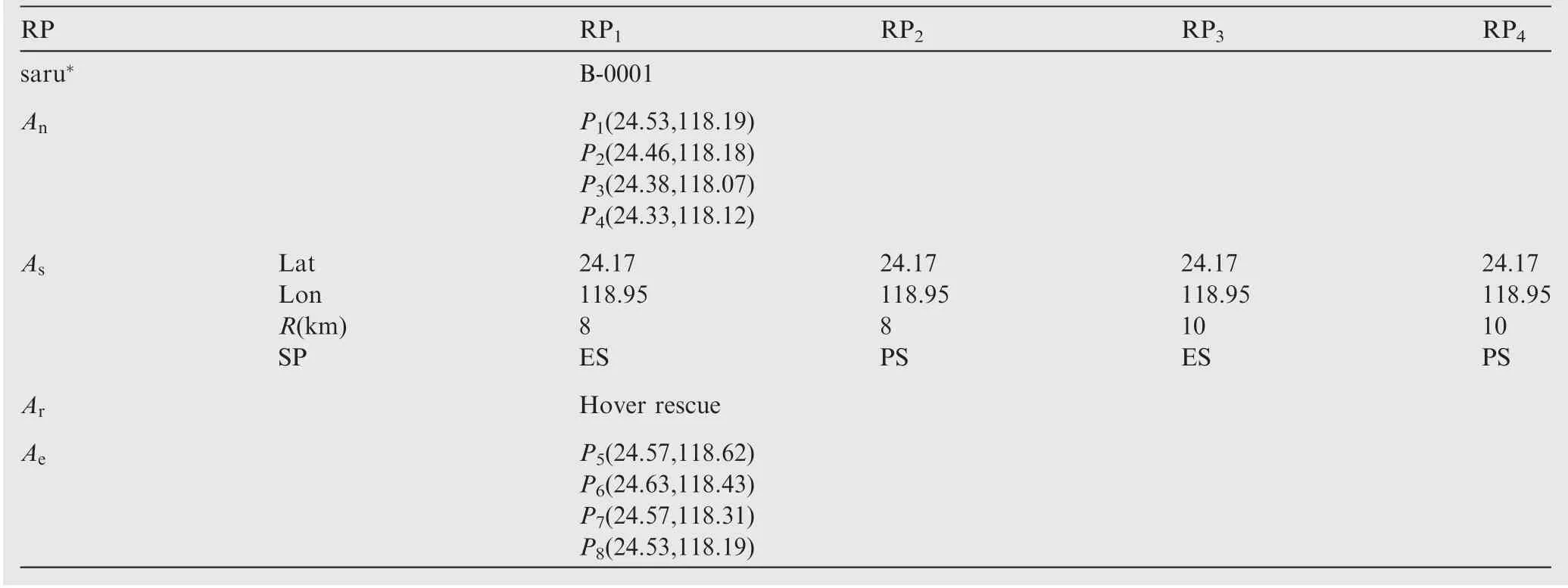
Table 4 Details of four response plans.

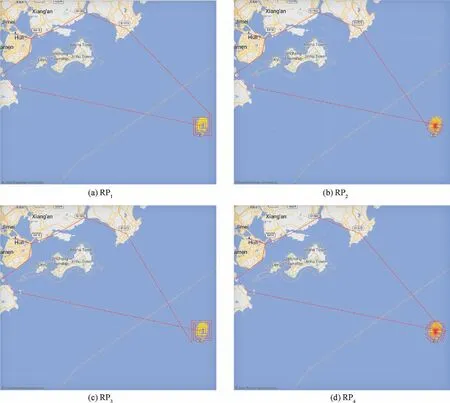
Fig. 14 Schematic of response plans.

5.2. Calculation of subjective weight

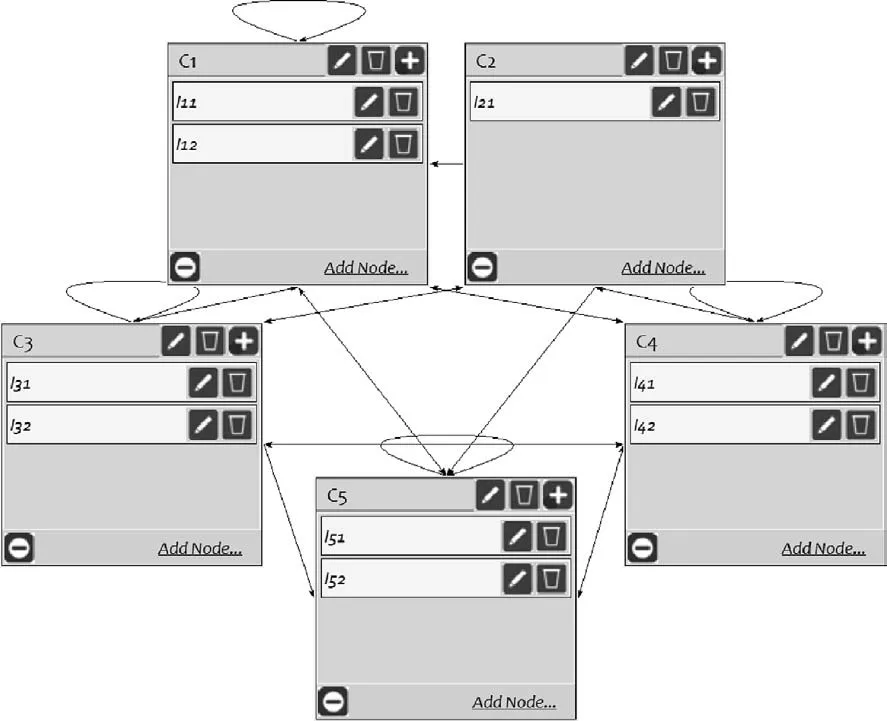
Fig. 15 ANP model for EIS of response plan.

When using ANP method to analyze the EIS of response plan,the first priority is to determine the candidates and the number of it.Maritime accident tended to occur randomly,which must be responded as quickly and effectively as possible.Therefore,the International Maritime Organization(IMO)and the International Civil Aviation Organization (ICAO) set multi search and rescue responsible areas.As a result, in the field of MSAR, the experience and knowledge of different experts are also different, which directly leads to the inconsistent of judgement.The classical Delphi method can solve above problems to some extent.

Fig. 16 Subjective weight of EIS.

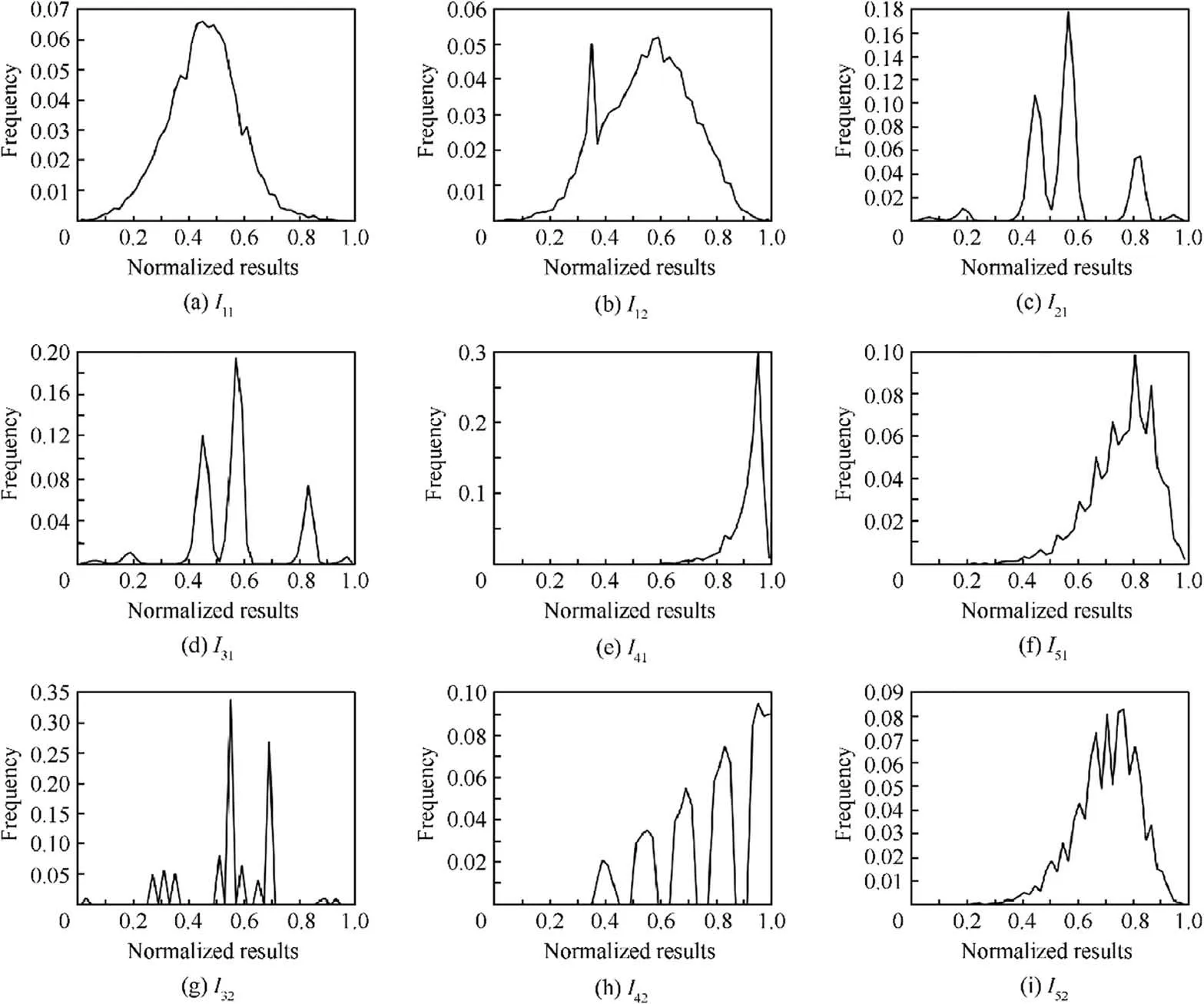
Fig. 17 Normalized frequency distributions in RP1.

Because of the complexity of calculating process with ANP model,the Super Decision software is used in this paper,which developed by William and Rozann. The operation process of this softwareis introduced in many references, so the details are not repeated.Then the ANP model of EIS is established as shown in Fig.15,and Subjective weight of EIS is calculated as shown in Fig. 16.

5.3. Calculation of objective weight

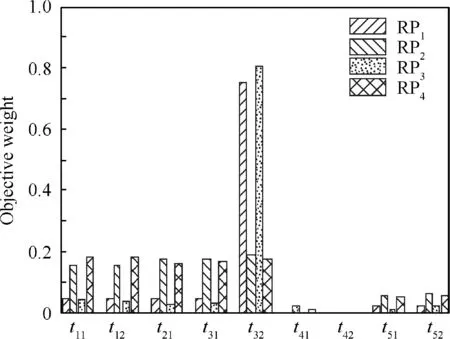
Fig. 18 Objective weight of indicators.

The four response plans are input into the prototype system for Monte Carlo simulation,and the simulation times is based on the distribution of all quantitative indicators tend to be stable.According to the simulation experiment,when the times of simulation is greater than 8000, all indicator distributions are convergent to a corresponding fixed distribution, so the simulation times is chosen as 10 000.

The simulation output value of each indicator is normalized into interval[0,1],which is divided into 50 subintervals to calculate the frequency distribution. Take the distribution of quantitative indicator results in RPas an example, which is shown in Fig. 17.

According to the statistical results of the above simulation data,the subjective weight of indicators under the influence of UFs can be calculated, as shown in Fig.18.Then the comprehensive weight of them can be obtained as shown in Fig. 19.

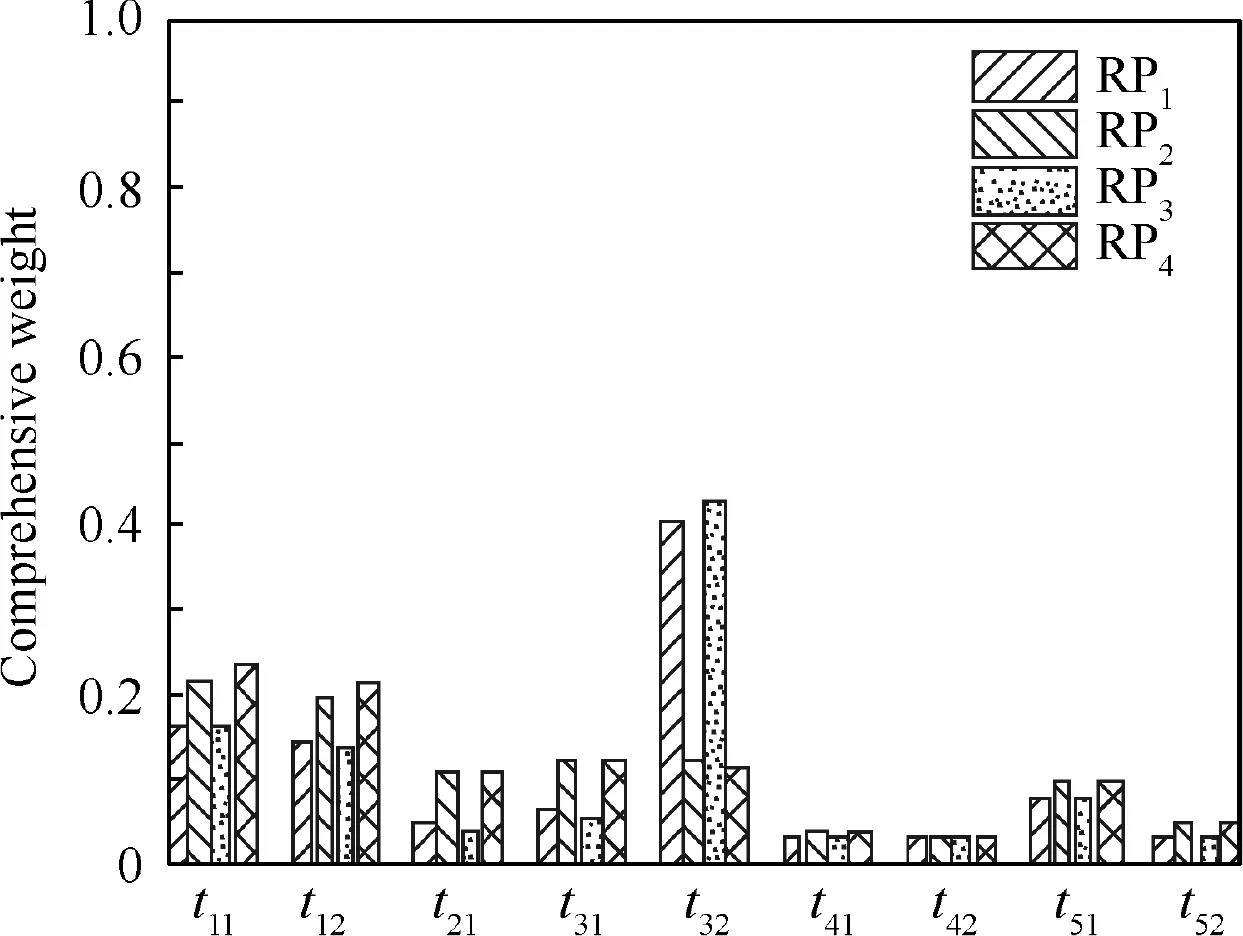
Fig. 19 Comprehensive weight of indicators.

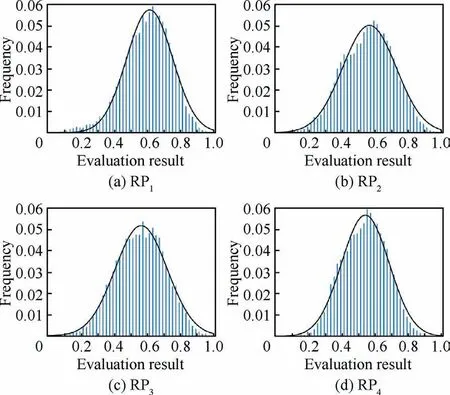
Fig. 20 Frequency distribution and fitting normal distribution curve of evaluation result.

It can be seen that the subjective weight of Iis significantly higher than that of other indicators. So UFs have the greatest influence on the coverage of helicopter searching mission area. Moreover, the objective weight of RPand RPis significantly greater than that of RPand RP,indicating that the influence of UFs on ES is greater than that of the PS.

Another important information is that the objective weight of Iin each response plan is zero.The reason is that the mission scenario in this paper assumes that the number of people in distress is 10, which is within helicopter rescue capability.Additionally, the distance between helicopter base and maritime accident is close, so the helicopter has enough time to search and rescue the distress ship.

The analysis above shows that UFs have different impacts on different response plan to the same mission scenario.Adapting the UMAD model and the prototype system can adjust the weights pertinently on the basis of comprehensively considering both subjective and objective factors. This methodology can help highlight the role of key indicators in the comprehensive evaluation results. And then the sensitivity of UFs to indicators will be analyzed, but this is not the main problem to be solved in this article.

5.4. Comprehensive evaluation result

According to the above result of indicator values, and the obtained comprehensive weights, it can be obtained that the comprehensive evaluation results of each helicopter MSAR response plan in each simulation can. In order to analyze different response plans intuitively, the results of them are pro-cessed based on the evaluation procedure. By this way, their frequency distribution and normal distribution fitting curve can be obtained as shown in Fig. 20.

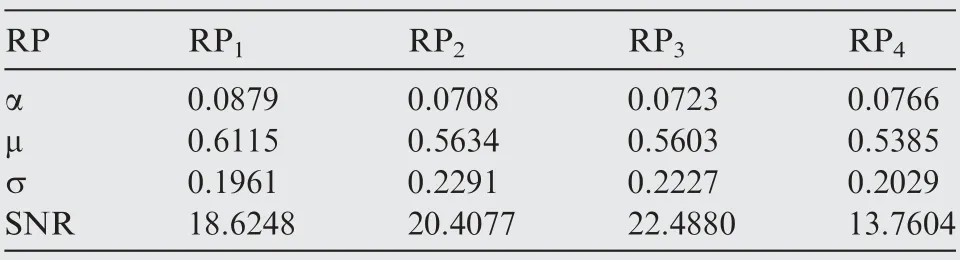
Table 5 Normal distribution fitting parameters.

The normal distribution fitting parameters of each response plan are summarized as shown in Table 5,where α,μ,σ express the parameters in Eq. (18). At the same time, the robustness measurement results SNR of each response plan can be obtained.

The normal distribution fitting results of all response plans are compared and analyzed, as shown in Fig. 21. The xcoordinate corresponding to the peak position of the curve represents the mean value of the evaluation result. This position indicates the average efficiency that can be achieved when the corresponding response plan is adopted. The y-coordinate corresponding to the peak position of the curve represents the probability density when the response plan achieves the average efficiency. In other words, what probability can the average efficiency achieves when the response plan is executed.Two key information can be deduced from the analysis above.When it comes to a similar peak probability density, the greater the mean value is, the higher the average efficiency can reach. When it comes to a similar mean value of response plan, the higher the peak probability density is, the greater probability of average efficiency the response plan can achieve.When the evaluation results of two RPs are similar, as the fitting curves of RPand RPin Fig.21,the SNR can be used for further comparing and analyzing.And the greater the SNR is,the higher the stability that response plan evaluation result locates near the average efficiency will be. Through these descriptions,the RPis the optimal helicopter MSAR response plan among the four response plans studied in this paper,which is also consistent with the reality.

5.5. Discussion

The specific evaluation procedure of helicopter MSAR response plan is discussed sufficiently in this part. Through the above analysis, it can be seen that the methodology proposed in this paper can evaluate and analyze multiple response plans of the same scenario, by which the optimal plan can be obtained.By this way,the corresponding relationship between MSAR scenario and its optimal response plan can be found.

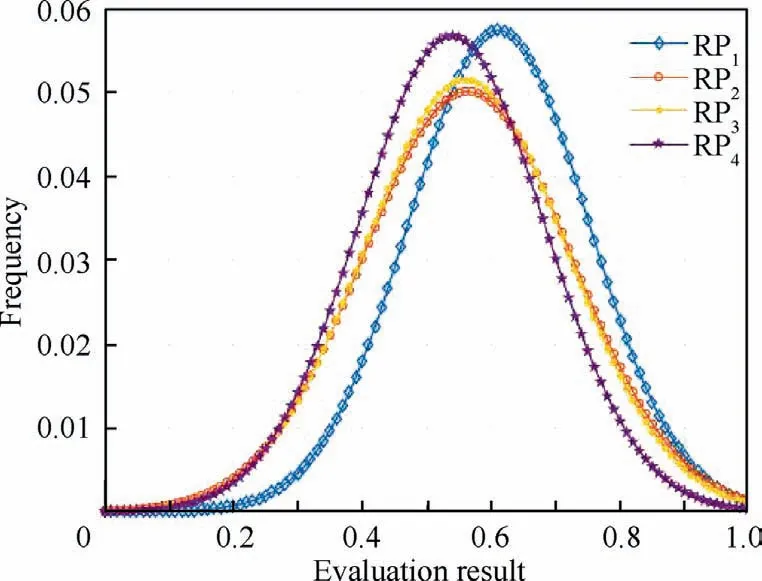
Fig. 21 Comparison of fitting results.

Therefore, a large number of evaluation analysises can be carried out on the same mission pattern, taking the mission pattern described in this paper as an example.And a database of optimal response plan to deal with maritime accident can be formed. Then based on this database, Case-Based Reasoning(CBR) can be used to do decision support for the same kind of mission. Furthermore, it will be possible to adequately explore the design space of helicopter performance parameters.To achieve this purpose, the mission scenario and optimal response plan must be remained unchanged. While the helicopter MSAR performance parameters are modified according to the Design of Experiment(DoE).At last,the optimal design space can be determined through the analysis of evaluation results. These significant works will be carried out in the following research.

6. Conclusions

(1) The UMAD framework evaluating helicopter MSAR response plan is proposed, which is based on singlehelicopter-single-flight mission pattern. Then the definition of response plan and UFs are studied. After that,the influence mechanism of UFs is revealed based on Multi-Agent method, and the mission flow is analyzed based on DEVS method.

(2) The EIS of response plan is established from the two aspects of safety and efficiency, which includes 5 evaluative criteria and 9 evaluative indicators. The subjective weights are calculated by ANP method, and objective weights are calculated by entropy weight method. Then the comprehensive weight is obtained by integrated processing.

(3) The evaluation process of helicopter MSAR response plan is sorted out,and the large sample of indicator simulation results are calculated by Monte Carlo simulation. Then these original datas are processed based on marking standard. On this basis, the probability and robustness of response plan are obtained with the comprehensive weight.

(4) Comprehensively considering the UMAD framework,EIS and evaluation procedure, a framework of simulation evaluation system for helicopter MSAR response plan is proposed.Take this as basis,the simulation evaluation prototype system is established, the function of which includes scenario editing, decision making,response plan simulation and comprehensive evaluation.

(5) Through an application example,it is illustrated that the evaluation methodology proposed in this paper can comprehensively evaluate the helicopter MSAR response plan with uncertainty. And the optimal plan can be screened out through analysis of the evaluation results, which will play a significant role in decision support.

The helicopter MSAR response plan is the basis of effective response to deal with maritime accident, and decision makers can improve their response efficiency through analysis of its comprehensive evaluation result. In this paper, the methodology for effectively evaluating response plan considering UFs is proposed, then the feasibility and practical significance of this methodology are verified by an example.Through analyzing the universality,it can be seen that this methodology is not only applicable to the mission pattern studied in this paper,but also used to evaluate the response plans of other emergencies.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

The authors are grateful to Mr. Zhao Zhang, Mr. Haidong Zhuang and Mr.Weining Zhao in XiaMen LanHaitian Information Technology CO.,LTD., for providing the drift information. They also thank the anonymous reviewers for their critical and constructive review of the manuscript. This study is supported by the Research Project from Ministry of Industry and Information Technology of People’s Republic of China.