Reduced order model for unsteady aerodynamic performance of compressor cascade based on recursive RBF

Jiwei HU, Hnru LIU,b,*, Yn’gng WANG, Weixiong CHEN, Yn MA

a School of Power and Energy, Northwestern Polytechnical University, Xi’an 710072, China

b Yangtze River Delta Research Institute, Northwestern Polytechnical University, Taicang 215400, China

KEYWORDS Compressor cascade;Neural network;Recursive radial basis function;Reduced order model;Unsteady flow

Abstract Based on Recursive Radial Basis Function(RRBF)neural network,the Reduced Order Model(ROM)of compressor cascade was established to meet the urgent demand of highly efficient prediction of unsteady aerodynamics performance of turbomachinery. One novel ROM called ASA-RRBF model based on Adaptive Simulated Annealing (ASA) algorithm was developed to enhance the generalization ability of the unsteady ROM. The ROM was verified by predicting the unsteady aerodynamics performance of a highly-loaded compressor cascade. The results show that the RRBF model has higher accuracy in identification of the dimensionless total pressure and dimensionless static pressure of compressor cascade under nonlinear and unsteady conditions, and the model behaves higher stability and computational efficiency.However,for the strong nonlinear characteristics of aerodynamic parameters,the RRBF model presents lower accuracy.Additionally,the RRBF model predicts with a large error in the identification of aerodynamic parameters under linear and unsteady conditions. For ASA-RRBF, by introducing a small-amplitude and highfrequency sinusoidal signal as validation sample,the width of the basis function of the RRBF model is optimized to improve the generalization ability of the ROM under linear unsteady conditions.Besides, this model improves the predicting accuracy of dimensionless static pressure which has strong nonlinear characteristics. The ASA-RRBF model has higher prediction accuracy than RRBF model without significantly increasing the total time consumption. This novel model can predict the linear hysteresis of dimensionless static pressure happened in the harmonic condition,but it cannot accurately predict the beat frequency of dimensionless total pressure.

Nomenclature ARX AutoRegressive with eXogenous input ASA Adaptive Simulated Annealing DMD Dynamic Mode Decomposition DNS Direct Numerical Simulation ERA Eigen-system Realization Algorithm HB Harmonic Balance method LES Large Eddy Simulation POD Proper Orthogonal Decomposition RANS Reynolds-Averaged Navier-Stokes RBF Radial Basis Function ROM Reduced Order Model RRBF Recursive Radial Basis Function x Input vector of model y Output vector of model b Bias vector of model φ Basis function μ Center vector of basis function σ Width of basis function w Weight matrix of model N Number of neurons in the hidden layer m Delay order of input n Delay order of output f Perturbation frequency k Reduced frequency A Relative amplitude ω Dimensionless total pressure π Dimensionless static pressure Subscript nor Normalization of aerodynamic parameters

1. Introduction

The aerodynamics performance improvement of the modern turbomachinery benefits from the deep understanding of the internal flow characteristics of turbomachinery. With the development of advanced measurement and high-fidelity numerical simulation in the field of fluid mechanics, the data amount of nonlinear and unsteady increases exponentially.The cost of obtaining the aerodynamic parameters of the full-order system and massive data processing has become bottleneck problem for the further research of turbomachinery aerodynamics.In compressor internal flow,due to the periodic rotor/stator interaction,the flow condition of downstream stator cascades is time varying, which is called dynamic inflow.Under dynamic inflow conditions, compressor cascade flow has strong nonlinear and unsteady characteristics. In order to improve the computational efficiency of complex unsteady flow field or deepen the understanding of high-dimensional nonlinear flow mechanism, researchers have developed a variety of data-driven ROMs for unsteady flow field since the 1990 s. These ROMs are widely applied in the fields of fluidstructure coupling,aerodynamic shape optimizationand flow control.These studies have accumulated many valuable results and shown promising prospects of ROMs.

ROM is a low-order mathematical model obtained by approximate projection of a full-order system.The current ROMs are mainly divided into two categories. The first is based on characteristic mode of the flow field. The essence of this method is to describe the full-order flow field motion with a set of low-dimensional Eigen-modes, and then project the complex unsteady flow field into the space of Eigen-modes by Galerkin or Krylov method. Typical methods include the Proper Orthogonal Decomposition(POD)and the Dynamic Mode Decomposition (DMD).Kang et al.studied the application of POD-Galerkin ROM method in prediction of unsteady flow field of NACA0012 airfoil.DMD is also widely used in subcritical cylindrical vortex-induced vibration,dynamic stall of wingsand transonic buffeting.Recently,Kou and Zhangproposed a DMD method with exogenous input and verified its effectiveness in modeling flow around cylinders and airfoils.

The other one is based on system identification, which essentially uses the mathematical mapping between the input and output data of the fluid system to establish a low-order transfer function or state-space model instead of a full-order system. Eigen-system Realization Algorithm (ERA)and AutoRegressive with eXogenous input (ARX) modelare two typical dynamic linear models for identifying the flow characteristics under the pre-assumption of small perturbations. Gao et al.used ARX model to study the problem of transonic single-degree-of-freedom flutter of airfoil, and obtained two prerequisites for the occurrence of this problem.Winter et al.used dynamic linear model and small perturbation method to accurately reproduce the unsteady aerodynamic force of AGARD 445.6 airfoil, which also had potential in aero-elastic design and optimization. When the external disturbance of unsteady system is strong enough,the dynamic nonlinear identification method should be used for characteristic analysis. Huangand Kouet al. used Wiener model with series structure to identify nonlinear unsteady aerodynamic loads of transonic flows of airfoil.Winter and Breitsamterestablished the variable Mach number aerodynamic model of AGARD 445.6 airfoil using fuzzy neural network and predicted the flutter boundary well.

During this period,Dowell and Hall applied Harmonic Balance method (HB)to modeling unsteady systems. Strictly speaking, based on Fourier series, to solve the unsteady flow field in the frequency domain, HB does not realize the reduction order of the model, therefore, it does not belong to ROM.Meanwhile, this method needs to solve the unsteady flow field repeatedly in frequency domain for different structures and aerodynamic parameters, so it is not suitable for the analysis and design of multidisciplinary coupling parameters.

In conclusion,ROM has been widely studied in the field of outflow, and has made many achievements. Compared with the external flow,the complex internal flow of turbomachinery is highly nonlinear and unsteady due to the existence of strong adverse pressure gradient and rotor-stator interference.At present, researchers mainly use numerical methods such as RANS,LES and DNS for flow prediction and flow mechanism analysis,which results in a huge amount of CFD calculation in the aspect of multidisciplinary coupling in the study of internal flow of turbomachinery and greatly restricts the engineering application of numerical research. The ROM method will undoubtedly have an important prospect in the understanding of the mechanism of internal flow, aerodynamic optimization and flow control. It is of great significance to develop an efficient aerodynamic ROM for turbomachinery.

According to the published literature, there are few studies on ROM method in internal flow. Whether ROM based on external flow can be applied to internal flow still needs to be further studied. Therefore, taking the dynamic inflow of high-load compressor cascade as the research object,this paper uses RRBF neural networkto establish and verify the ROM for turbomachinery. In addition, the ASA-RRBF method,which is based on ASA algorithm is further developed to enhance ROM generalization ability. It broadens the applicability of ROM in turbomachinery and provides efficient design and research methods for relevant researchers.

2. Methodology

2.1. Radial basis function neural network

The RBF neural network was proposed by Broomhead and Loweand Radial Basis Function was adopted as the activation function of hidden layer of the three-layer forward network. The scheme of the RBF neural network is shown in Fig. 1.

The input vector is x ∈R，and the output vector is y ∈R.Each input/output vector forms a sample: ［x，y ］. The number of neurons in the hidden layer is N,the bias vector of network is b, and the basis function is φ.

The output of the RBF neural network can be expressed as:

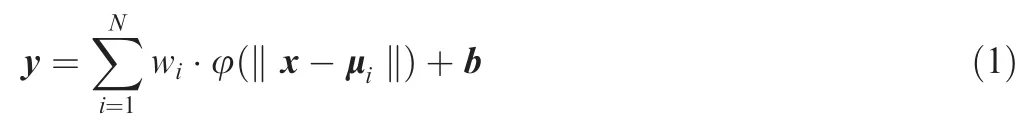
where wrepresents the node weight of hidden layer to output layer.

In the past,researchers mostly use the Gaussian basis function to establish such ROMs,and those ROMs have relatively good performance.Therefore, Gaussian basis function is also used in this paper. The equation is:

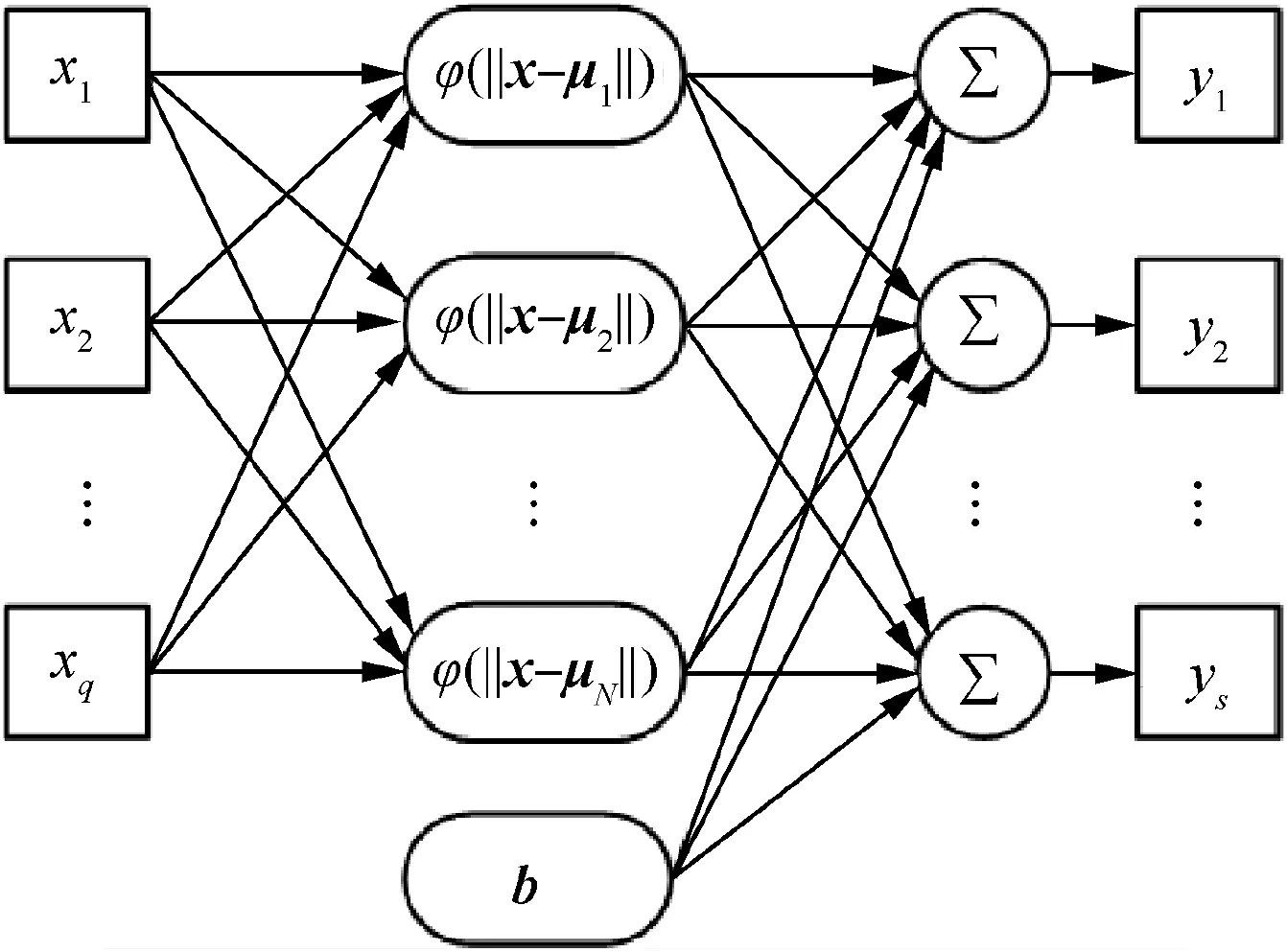
Fig. 1 Scheme of RBF neural network.

where Φ= （ΦΦ）Φ. For a network with a bias b,researchers simply add a column vector with all one elements to the last column of the matrix Φ, and then the bias b is included in the weight matrix w.

2.2. Recursive radial basis function neural network

Considering the time-delay effect of unsteady systems,Zhangdeveloped a RRBF neural network model based on the Nonlinear AutoRegressive with eXogenous inputs model(NARX).The model introduces input and output delay structure to accurately describe the unsteady effect of the system. The unique advantage of this model is that the modeling time is short. The scheme of the RRBF neural network is shown in Fig. 2.

The RRBF network output can be expressed as:

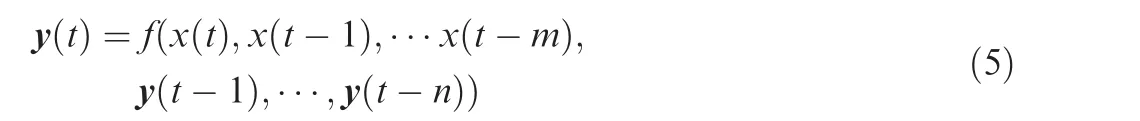
where m and n are the delay orders of input and output respectively, and the f(·) is the expression of the RBF.

This paper studies the aerodynamic performance of a compressor cascade under dynamic inflow conditions. Therefore,the input is the angle of attack at inlet:

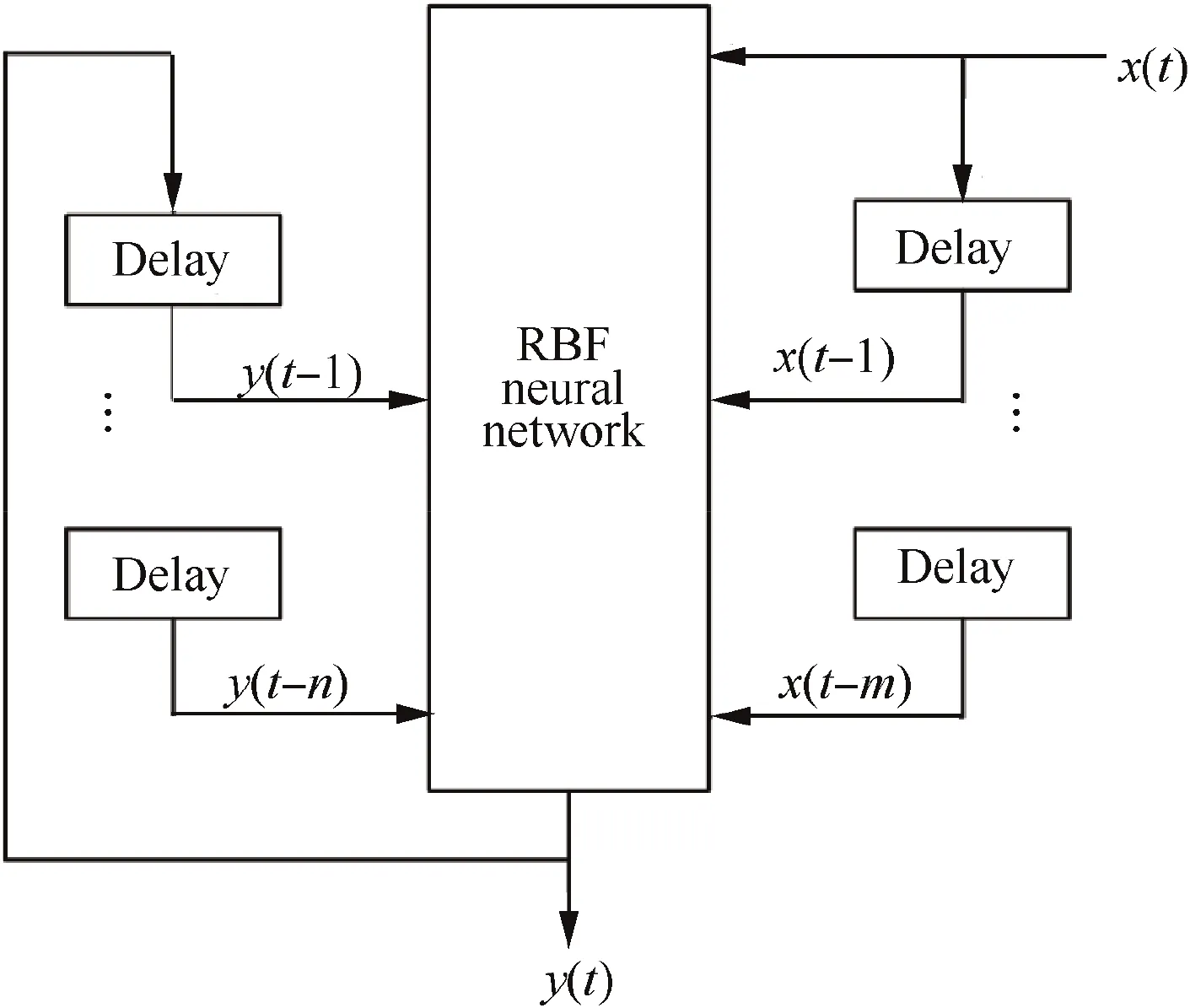
Fig. 2 Scheme of RRBF neural network.

The output is the dimensionless total pressure and dimensionless static pressure:

2.3. Optimization of basis function width

The main problem of nonlinear ROMs is the less accuracy of predicting linear features.In order to enhance the generalization ability of the established nonlinear ROM to linear features without decaying the identification accuracy of training sample, this paper introduces a small-amplitude highfrequency sinusoidal signal as validation sample to optimize the width of the traditional RBF model. Fig.3 shows the process of training and prediction of the novel ROM.The process is as follows:

(1) Training sample is used to obtain the RRBF neural network with uniform width, including center vector,weight and bias.

(2) The Root Mean Square Error (RMSE) of the predicted value of the validation sample is regarded as the cost function. The optimization interval is the small value range centered on the uniform width.Keeping the center vector unchanged, ASA algorithm is used to optimize the width of the basis function of the RRBF model.The modified ROM with non-uniform width is ASARRBF model.

The reason for using the ASA algorithm is that the optimal solution obtained by this algorithm is independent of the initial state. This algorithm is asymptotically convergent and has been proved theoretically to converge to the global optimal solution with probability of one.

(3) Test samples are used to test the performance of the ASA-RRBF model.

3. Unsteady flow simulation

The main geometric parameters of a highly-loaded compressor cascade are given in Table 1. The structure of the cascade is shown in Fig. 4.

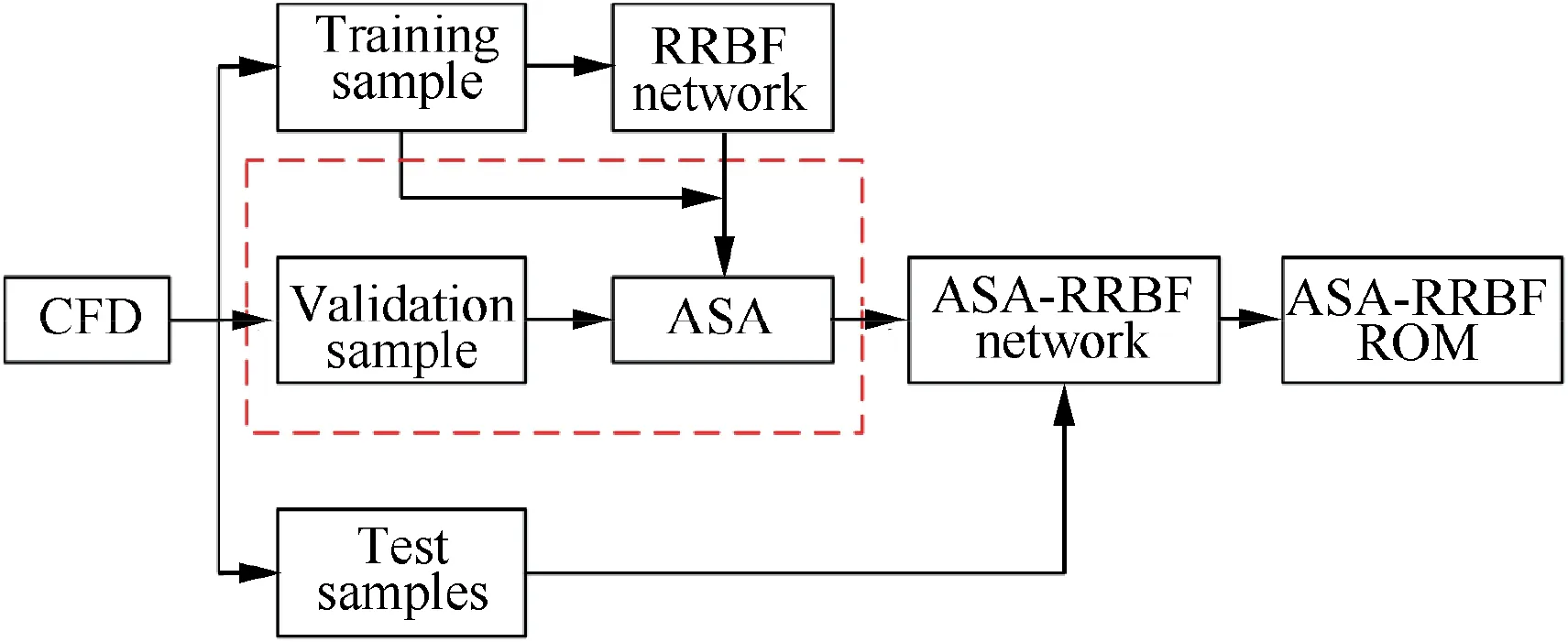
Fig. 3 Flowchart of ROM training and prediction.

Table 1 Main geometric parameters of cascade.

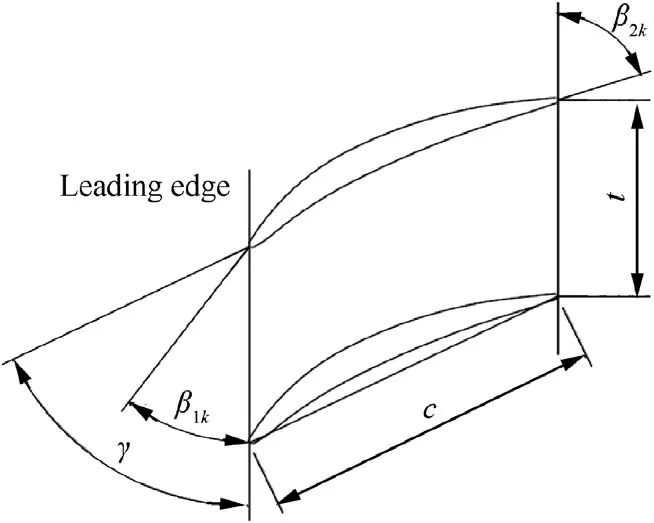
Fig. 4 Structure of cascade.

The inlet of the computational domain is one time chord length from the leading edge of the cascade, and the outlet is 1.5 times chord length from the trailing edge of the cascade.The grid adopts the H-O-H structured grid with a total number of 30196 grids and the Yof the near wall grid is less than one. The topology of the grid is shown in Fig.5.For the twodimensional cascade simulation,the unsteady RANS equation is solved by ANSYS Fluent software with the k-ω SST (Shear Stress Transport) turbulence model. The basic flow condition is that the inlet Mach number is 0.6 and the angle of attack is 0°. The physical time step is 1.5×10s. The convergence criterion set in this paper is that the iteration residual within each time step drops below 1×10.For dynamic inflow condition, the angle of attack is changed with time varying. The time-varying angle of attack i(t)of compressor cascade,including randomly varying and harmonic sinusoidal varying, is taken as the input signals.

4. Validation

4.1. Training sample

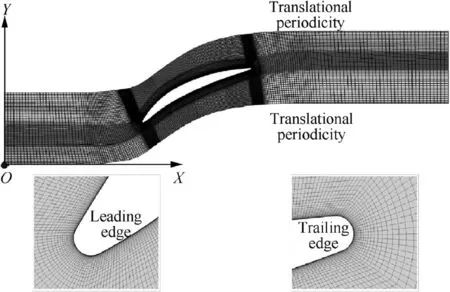
Fig. 5 Topology of grid.

In order to verify the effectiveness of the ROM, the highlyloaded compressor cascade performance under dynamic inflow is modeled in this paper.The training sample is Filtered White Gaussian Noise (FWGN) signal, which contains 1800 time steps. The time step value of the sample is consistent with the simulation of unsteady flow field.Fig.6 shows the characteristic of the training sample. The ordinate in Fig. 6(a) represents the angle of attack,and the maximum amplitude value is 6°. The Power Spectral Density (PSD) distribution shown in Fig. 6(b) indicates that the training sample covers a wide reduced frequency band with strong energy in the range of 0-16 dB.Therefore,the sample can be used to identify aerodynamic parameters under harmonic conditions of different frequencies.

The reduced frequency k, which is used to describe the strength of the unsteady effect, is defined as:

The input/output parameters of the ROM can be customized according to the research requirements. Considering that the compressor cascade mainly focuses on the inlet/outlet aerodynamic parameters,the unsteady instantaneous values of the inlet/outlet total pressure and static pressure are taken as the prediction results. Some researchers point out that modeling each parameter separately can improve the prediction accuracy of ROM.For the purposes of this article,four separate ROMs need to be established.The main research content of this paper is to establish and verify the fast prediction ROM of aerodynamic parameters in turbomachinery internal flow,and further develop methods to improve the generalization ability of ROM.In order to improve the efficiency of research,the instantaneous values of inlet/outlet total pressure and static pressure are dimensionless according to the characteristics of the aerodynamic parameters in the cascade.

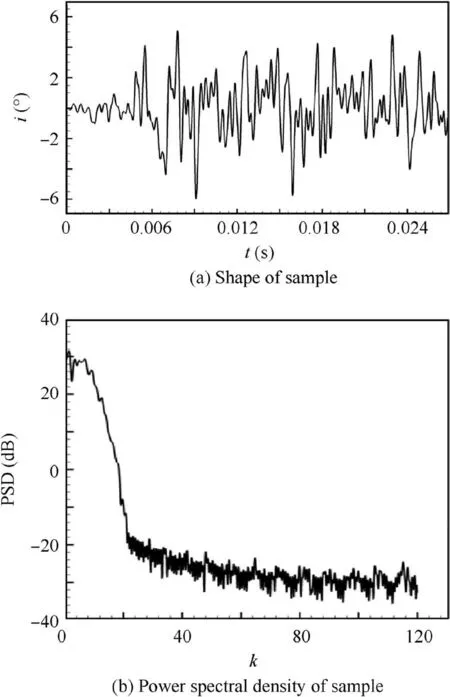
Fig. 6 Characteristic of training sample.

Fig.7 shows the characteristics of normalized aerodynamic parameters with different relative amplitudes. The relative amplitude A is defined as:

where the P(t ) is the instantaneous outlet static pressure and the π is the dimensionless static pressure.

As can be seen from Fig. 7, the normalized aerodynamic parameters are almost collinear when A=0.05 and A=0.02. This indicates that these working condition are linear.When A is greater than 0.05,the normalized aerodynamic parameters constantly deviate from the linear line. The degree of deviation increases with the increase of A, which indicates the enhancement of nonlinear characteristics.

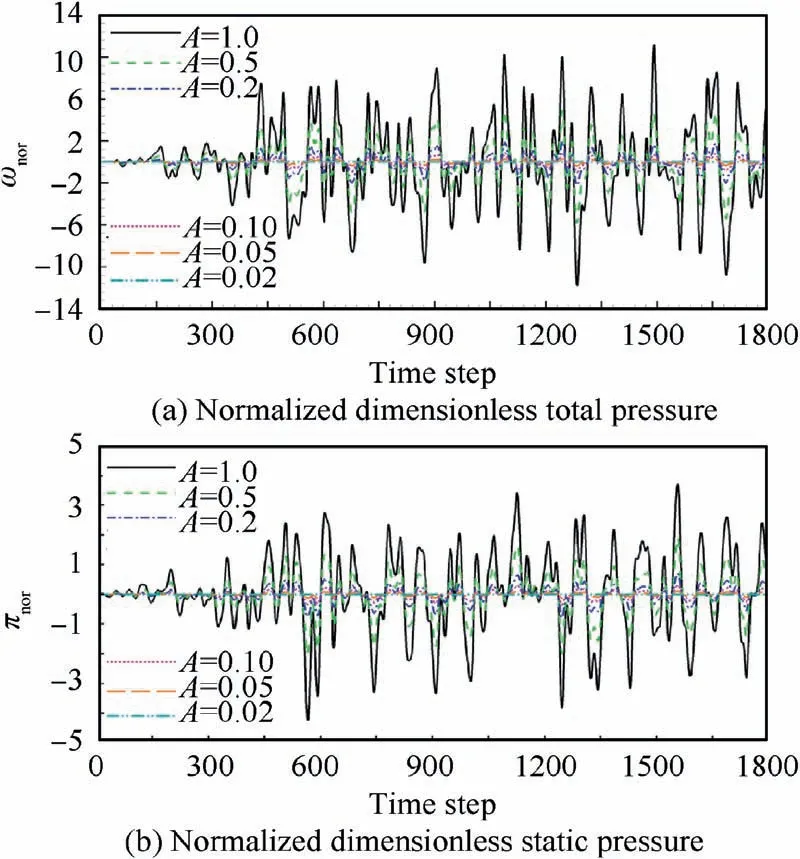
Fig. 7 Normalization of aerodynamic parameters.

4.2. ROM for unsteady aerodynamic performance

The FWGN signal with relative amplitude A=1 is used as the training sample. The delay orders can be selected by the Akaike information criterionor the Bayes information criterion.In addition, the approximate optimal delay orders can be selected by increasing the delay orders gradually and evaluating the performance of the model. In this paper, the delay orders are selected by trial-and-error method. The m=120 and n=120 are the delay order of input and output of the ROM respectively.By decentralized the data,the model is zero input and zero output. Therefore, the first several unknown output values are initialized to zero. The number of hidden layer neurons N is 100, and the uniform width σ is 24.

In order to improve the generalization ability of nonlinear ROM to linear conditions, a sinusoidal signal of small amplitude and high frequency is introduced as a validation sample to optimize the width of the basis function of the RRBF model. The amplitude of the validation sample is i=0.25°,and the reduced frequency is k=8.991. The width used for ASA optimization ranges from 23.95 to 24.05, and the maximum number of iteration steps is L=2000. Fig. 8 and Fig. 9 are the aerodynamic parameters identification of the training sample and the validation sample predicted by traditional RRBF and ASA-RRBF model.

Table 2 shows the RMSE of identification of training and validation samples. It can be seen that the identification accuracy of the two ROMs for the training sample is basically consistent.For the validation sample,the three distribution curves of the dimensionless total pressure are basically the same,while the distribution curve of dimensionless static pressure predicted by RRBF model deviates greatly from CFD results.The prediction accuracy of RRBF model for dimensionless static pressure is not as good as the dimensionless total pressure.It shows that the dimensionless static pressure has stronger nonlinear characteristics,which makes it difficult to predict accurately with this ROM.By introducing validation sample in ASA-RRBF model, the identification accuracy of aerodynamic parameters especially dimensionless static pressure is improved significantly.

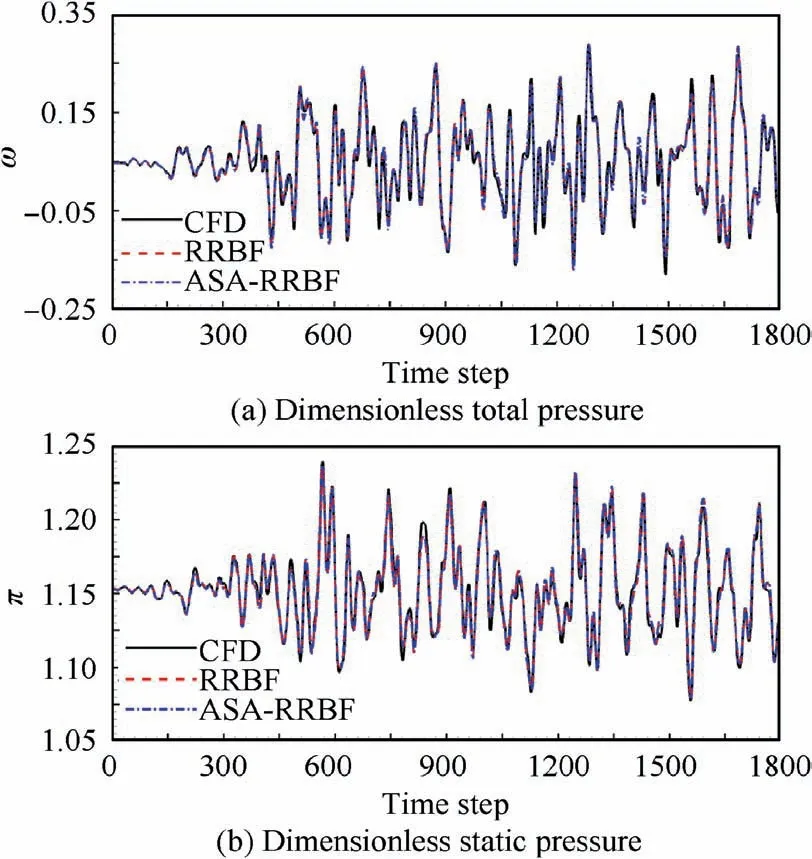
Fig.8 Identification of training sample.

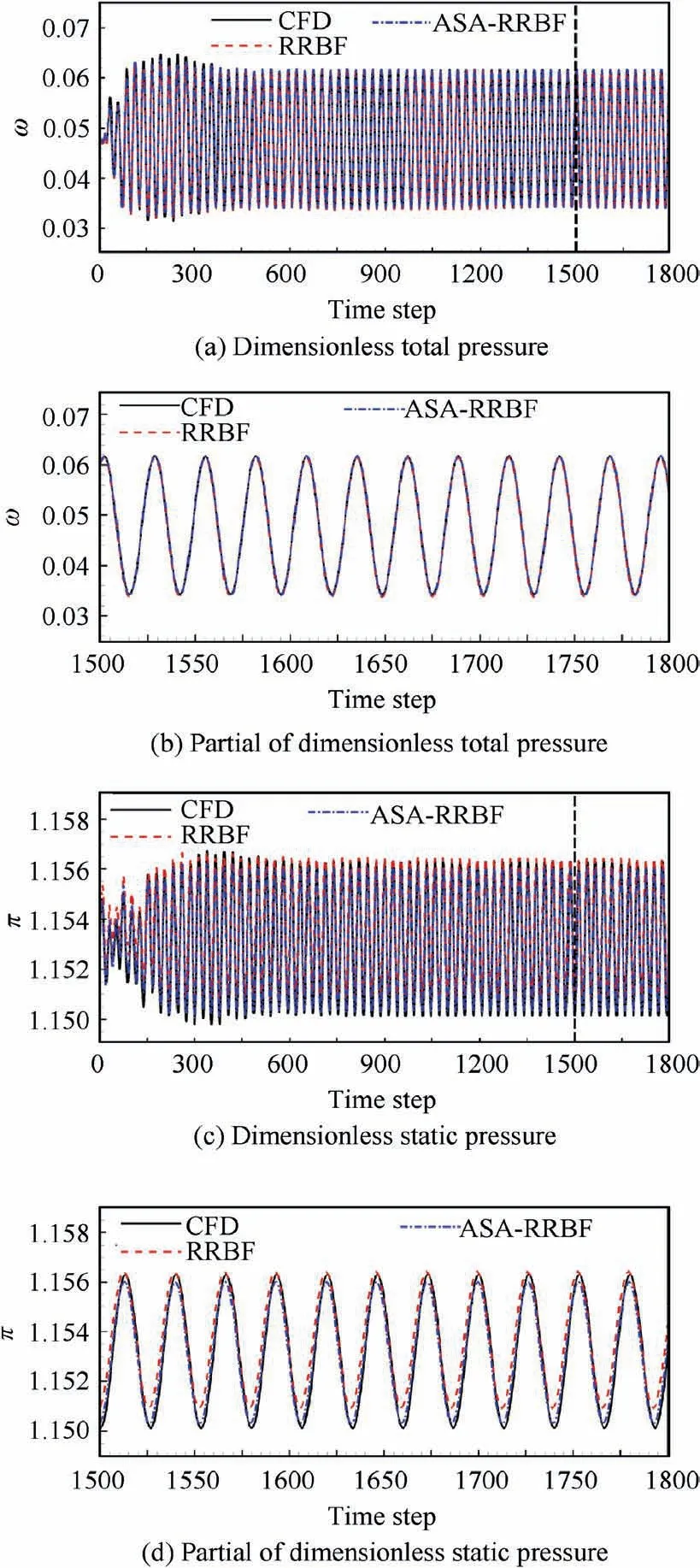
Fig. 9 Identification of validation sample.

4.3. Performance prediction under random conditions

In order to evaluate the effectiveness of the ROM and the effect of introducing validation sample, the prediction accuracy of two ROMs are compared for different test samples.The test samples included three groups of aerodynamic parameter responses with the same signal shape as the training sample. The relative amplitudes of the test samples are A=0.5,A=0.1 and A=0.02, respectively. The aerodynamic parameter response of test sample with different signal shape from the training sample is given to further verify the generalization ability of the model.The relative amplitude of this test sample is A=0.01.According to the above analysis of the character-istics of normalized aerodynamic parameters, the four test samples can cover conditions of nonlinear, weakly nonlinear and linear characteristics. Fig. 10 and Fig. 11 show the predicted results of the ROMs.

Table 2 RMSE of identification of training and validation samples.

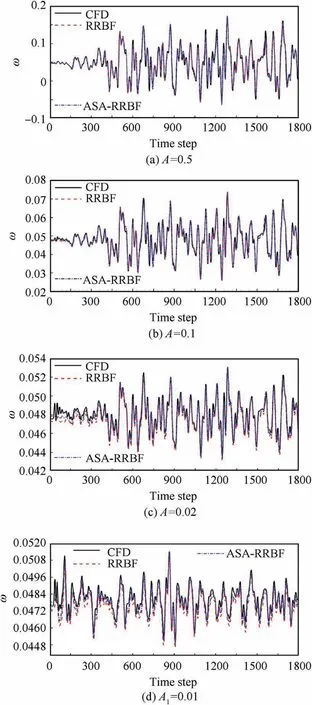
Fig. 10 Prediction of dimensionless total pressure.

Table 3 shows RMSE of identification of testing samples.It can be concluded that the prediction accuracy of the ROM for dimensionless static pressure is not as good as that of dimensionless total pressure. The reason is that dimensionless static pressure has strong nonlinear characteristics, which is consistent with the above conclusion of sample identification. When the relative amplitude is A=0.5 and A=0.1, the prediction of the two models for aerodynamic parameters are basically consistent with CFD results. However, as the relative amplitude decreasing,the deviation of aerodynamic parameters predicted by RRBF model increases, such as the relative amplitude A=0.02 and A=0.01. It shows that the nonlinear model obtained from the training sample of nonlinear working condition is not accurate enough for the prediction of linear working conditions. The prediction of the model may be distorted, especially in the prediction of dimensionless static pressure of the sample with a relative amplitude of A=0.01. The prediction accuracy of the ASA-RRBF model which introduces validation sample for the dimensionless total pressures under all amplitudes is basically consistent with RRBF. Moreover, the prediction accuracy of the model for dimensionless static pressure increases significantly in the case of relative small amplitude. It can be concluded that with the decreasing of the relative amplitude, the ASA-RRBF model can maintain high accuracy and stability in predicting both the nonlinear and linear conditions.

4.4. Performance prediction under harmonic conditions

For aeroelastic and flow control problems, the ROM needs to provide more accurate identification of aerodynamic parameters under harmonic conditions.In order to verify the generalization ability of the models under harmonic conditions, six groups of sinusoidal signal with an average angle of attack of zero are selected as test samples. The test samples include two sets of amplitude (i=2° and i=0.1°) and three sets of reduced frequency (k=8.991, k=7.193 and k=3.597).These frequencies are related to the passage frequency of upstream rotor blade.

Fig.12 and Fig.13 show the time evolution of aerodynamic parameters predicted by the model, and both contain more than ten cycles.It can be seen that the aerodynamic parameters predicted by the two models are basically consistent with the CFD results, and the local error of the model prediction is within the acceptable range.For the nonlinear condition,these two models can obtain high prediction accuracy. However,under the condition of i=2°and k=7.193,the dimensionless total pressure has beat frequency, which makes it difficult to accurately predict the distribution of aerodynamic parameters with the low order model.

Fig. 14 and Fig. 15 show the hysteresis loop results of the aerodynamic parameters predicted by the ROM model. As can be seen from the figure, for the dimensionless total pressure, both models provide relatively accurate responses at different frequencies, and the ASA-RRBF model seems more accurate. For dimensionless static pressure, RRBF model has large prediction error and distortion at different frequencies,while ASA-RRBF model still has high prediction accuracy.Under the condition of i=0.1° and k=8.991, the modified model predicts well the linear hysteresis loop of dimensionless static pressure.

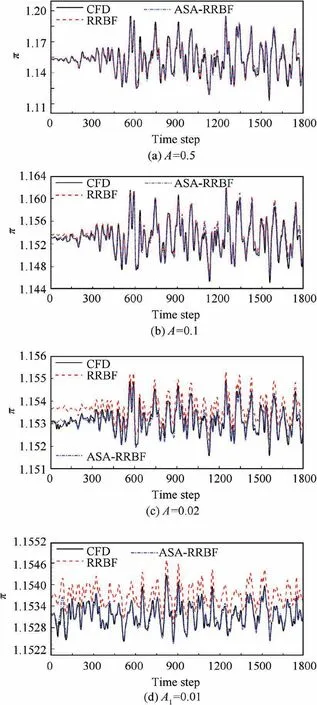
Fig. 11 Prediction of dimensionless static pressure.

4.5. Computational efficiency of ROM

Fig. 12 Time evolution of dimensionless total pressure.

Table 4 shows the time consumption comparison between CFD and ROM.For FWGN signal and sinusoidal signal samples of high-load compressor cascade with 1800 time steps,the time consumption of CFD to solve a single sample is about 36 h. It takes less than 10 s to build RRBF model. And then,the predicting time of the model for a single sample is less than 1 s. For ASA-RRBF model with validation sample, the time consumed in the modeling process is mainly in the process of optimization searching of adaptive simulated annealing algorithm. For the samples in this paper, the entire modeling time of adjusting model parameters using ASA algorithm is less than 10 min.

The Total Time Consumption (TTC) of the CFD refers to the total time of 10 samples calculated by CFD. The TTC of the ROM is the sum of the time used to model and predict the 10 samples.As can be seen,the TTC of the ROM is far less than that of CFD solution.The ASA-RRBF model can obtain stronger generalization ability without significantly increasing the TTC compared with RRBF model.

Table 3 RMSE of identification of test samples.

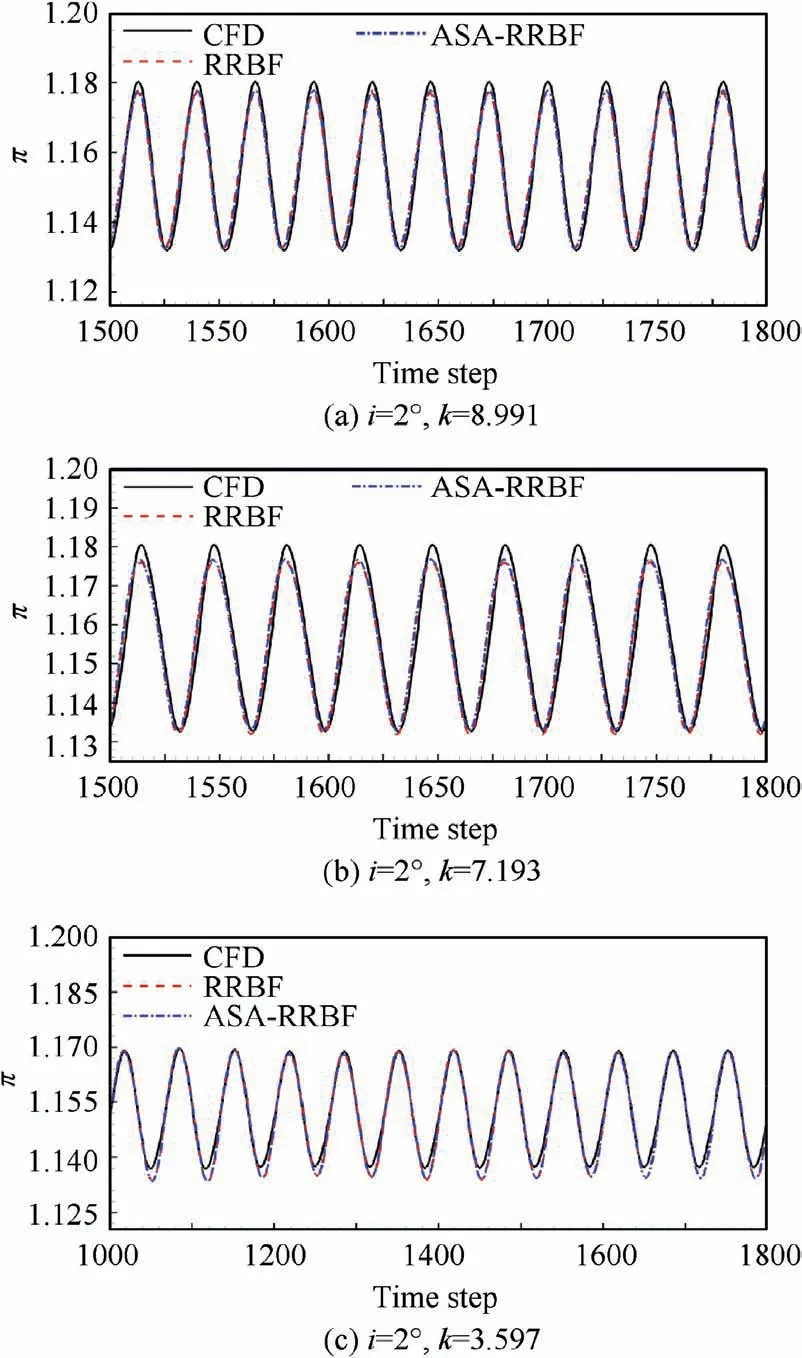
Fig. 13 Time evolution of dimensionless static pressure.

Table 4 Comparison between CFD and ROM time consumption.

5. Conclusions

In this paper,the Reduced Order Model(ROM)for prediction of aerodynamic performance of highly-loaded compressor cascade under unsteady inflow condition is established. A novel method to enhance the generalization ability of unsteady ROM is proposed. The main conclusions are as follows:

(1) The Recursive Radial Basis Function(RRBF)ROM has

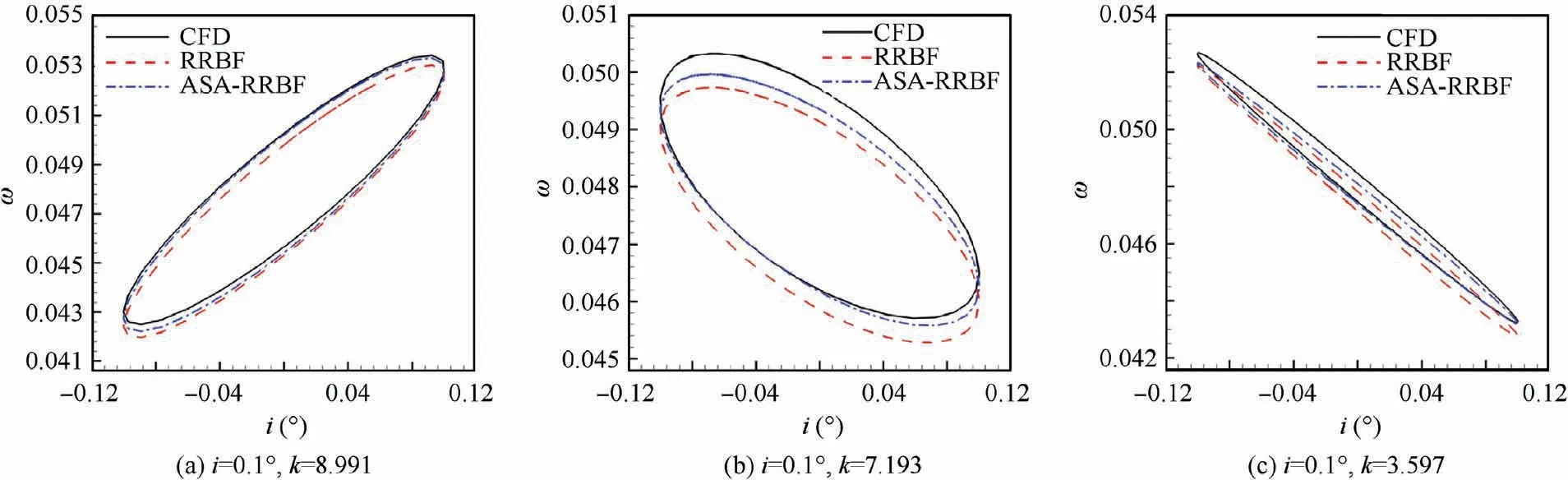
Fig. 14 Hysteresis loop of dimensionless total pressure.

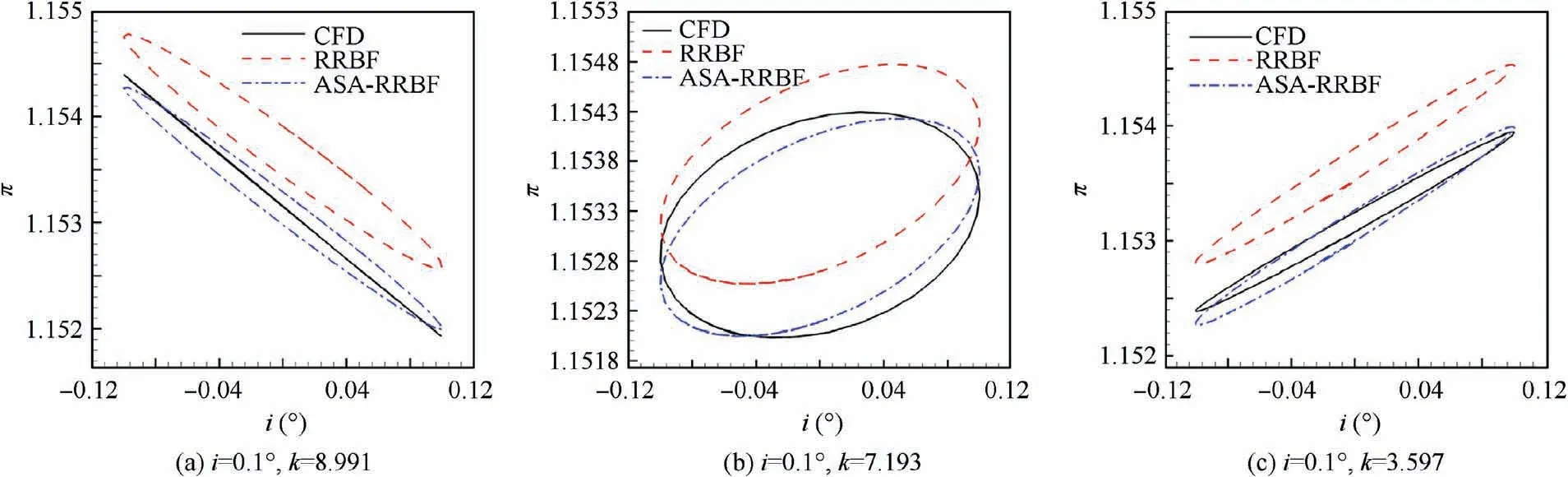
Fig. 15 Hysteresis loop of dimensionless static pressure.

higher accuracy in identification of the dimensionless total pressure and dimensionless static pressure of compressor cascade under nonlinear and unsteady conditions, and the model has higher stability and computational efficiency. However, for the strong nonlinear characteristics of aerodynamic parameters, the prediction accuracy of the RRBF model decays. The RRBF model predicts with a large error in the identification of aerodynamic parameters under linear and unsteady conditions.

(2) In terms of the ASA-RRBF model, by introducing a harmonics sinusoidal signal of small-amplitude and high-frequency as validation sample, the width of the basis function has been optimized and subsequently,the generalization ability of the ROM for linear unsteady conditions is improved. At the same time, this model improves the prediction accuracy of dimensionless static pressure under strong nonlinear characteristics.

(3) The ASA-RRBF model has higher accuracy than RRBF model without significantly increasing the total time consumption.The modified model can predict the linear hysteresis loop of dimensionless static pressure under harmonic condition, but it cannot accurately predict the beat frequency of dimensionless total pressure.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

s

This work was co-supported by National Science and Technology Major Project (No. 2017-II-0009-0023) and Innovation Guidance Support Project for Taicang Top Research Institutes(No. TC2019DYDS09). The authors would like to thank Dr.Jiaqing KOU of the Technical University of Madrid for his helpful discussing on the ROMs.