Discrete time multiple spacecraft formation flying attitude optimal control in presence of relative state constraints

Hossein MORADI PARI, Hossein BOLANDI

Department of Electrical Engineering, Iran University of Science and Technology, Tehran 009821, Iran

KEYWORDS Decentralized;Discrete time;Formation flying;Optimal control;Spacecraft;Virtual structure approach

Abstract This paper addresses the challenge of synchronized multiple spacecraft attitude reorientation in presence of pointing and boundary constraints with limited inter-spacecraft communication link.Relative attitude pointing constraint among the fleet of spacecraft has also been modeled and considered during the attitude maneuvers toward the desired states. Formation fling control structure that consists of decentralized path planners based on virtual structure approach joint with discrete time optimal local controller is designed to achieve the mission’s goals.Due to digital computing of spacecraft’s onboard computer,local optimal controller based on discrete time prediction and correction algorithm has been utilized. The time step of local optimal algorithm execution is designed so that the spacecraft track their desired attitudes with appropriate error bound.The convergence of the proposed architecture and stability of local controller’s tracking error within appropriate upper bound are proved. Finally, a numerical simulation of a stereo imaging scenario is presented to verify the performance of the proposed architecture and the effectiveness of the algorithm.

1. Introduction

Spacecraft Formation Flying (SFF) paradigm can make complex space missions,such as earth observatory/remote sensing,technology demonstration, earth science and space science,possible and cost effective.This main challenge related to this paradigm is the robust and reliable guidance and control algorithm for onboard systems.Several strategies and approaches have been proposed for control of SFF.These strategies are classified into three control approaches: leader-follower,behavioral, and virtual structure.The advantages and disadvantages of each approach have been discussed in literatures.Considering multiple criteria such as single point failure risk, reliability, flexibility and computational complexity, virtual structure provides an approach with fewer drawbacks.In this approach, the entire formation is treated as a single structure with central supervisor or multiple supervisors that calculate the desired states for every spacecraft in one virtual structure frame.When a large number of spacecraft are involved in the formation and/or the inter-spacecraft communication links are limited,it is difficult to implement the virtual structure approach with one central supervisor.In order to reduce the risk of central supervisor failure (singlepoint failure) and also the complexity of decision making for the whole members, the framework should be implemented with decentralized supervisors.Decentralized control eliminates these drawbacks by job sharing among participants and allowing each spacecraft to make decision based on the necessary status of other spacecraft in the formation.In the framework of virtual structure approach, the desired trajectories which are calculated by supervisors should be tracked by each spacecraft local controller. Because of attitude determination sensor’s limitations, tracking the desired trajectory may cause that the onboard attitude navigation faces problem.During the attitude maneuver, optical sensor’s (such as star tracker) performance degrades whenever bright objects such as sun or thruster’s illumination are present in their field of view.Therefore, one of the SFF guidance constraints is to keep the sun vector or neighbor spacecraft thruster’s vector(dynamic relative constraint)away from the star tracker’s field of view during maneuver.Therefore,we face Constraint Attitude Guidance and Control (CAGC) problem considered and discussed in the most recent literature.

Spacecraft formation flying control based on decentralized virtual structure approach was first introduced by Ren and Beard.An innovative architecture consisting of two Lyapanov based controllers has been utilized and the stability of whole system has been investigated. However, the proposed PD-Like controllers are unable to perform the mission in presence of constraints. Many approaches have been taken into place to solve the CAGC problem.Geometric approaches were proposed by Hablani, Spindler, and Frakes et al.to control a single spacecraft attitude, considering sun avoidance constraint. However, finding a feasible and safe path in the presence of multiple constraints is too complicated in this approach. Also, this approach cannot tackle dynamic relative states constraint.Frazzoli et al.proposed path planning with a randomized search tree method. In this paper, safe path is generated by a search tree algorithm but this method cannot guarantee finite time solution convergence. To overcome this dilemma, the convex optimization approach has been utilized by Kim et al..This approach can guarantee solution achievement with polynomial computation time if a solution exists.In this paper, a significant step has been taken in successive convexification of forbidden attitude constraints which are not convex in general.In Ref.20,the CAGC problem has been discussed for a single spacecraft maneuver with multiple pointing constraints. Even though a new cost function has been proposed in this article, due to the presence of root term in the cost function, inappropriate control signal can be generated,making the attitude control impossible. Moreover, possible dynamic relative attitude constraint has not been considered.Wu et al.modeled multiple pointing and boundary constraints in a single spacecraft CAGC problem and proposed a new time optimum path planning algorithm.The considered quadratic pointing constraints are not generally convex because their associated matrices are not sign definite. Therefore,the convex optimizer algorithm may fail to reach the global minimum solution.

Okoloko and Kim,using the convexification method proposed by Kim et al., investigated the CAGC. In this paper,consensus algorithm has been used to generate path toward desired attitude and synchronize the attitude of three connected spacecraft flying in a formation. Quaternion norm preserving term is considered in the consensus algorithm to prevent the quaternion unit norm violation. Then a continuous-time convex optimization local controller is designed to track the generated trajectories. If the consensus problem leads to a path that violates the forbidden attitude constraints, the algorithm stops and generates a new path repeatedly until the constraints have been made satisfied. This method has three drawbacks. First, there is no guarantee that the guidance algorithm generated a safe path in a finite time.The second drawback is the inability of the algorithm to satisfy relative state constraints between members. The third drawback is due to onboard implementation of proposed algorithm.The algorithm proposed by Okoloko and Kimcannot tackle the constraints in discrete-time implementation since the discrete-time implementation of a continuous time constraint optimization algorithm such as the algorithms proposed by Ye and Huand Fazlyab et al.may result in divergence.This is because, in a time-varying path tracking problem, the convergence and stability of tracking error are directly related to the digital sample time of algorithm execution.

In summary, reviewing the above approaches concludes that their main drawbacks are as follows. Relative dynamic pointing constraint among the spacecraft formation flying members has not been taken into account during maneuvers.Moreover onboard discrete time implementation of previous CAGC algorithm may result in pointing constraints violation.To overcome these drawbacks, the present investigation purposes an optimal strategy to tackle the static and relative state constraints in a formation flying mission. The main contribution of this paper is to introduce a new discrete formation flying attitude control structure in presence of pointing constraints. The new structure consists of a global PD-Like formation controller based on virtual structure approach and an optimal local controller. PD-Like controller generates the desired path nodes online.At the same time,optimal local controller generates necessary torques to track the desired states while satisfying multiple constraints defined as Linear Matrix Inequality (LMI). An appropriate algorithm implementation time step is calculated to guarantee the upper bound of tracking error.We claim that our formation flying control structure has been compatible in response to measurements taken at discrete time steps and its solution could provide control actions that can be implemented on digital control units.

In Section 2, first, some preliminaries explanation of the virtual structure coordination control has been introduced.Then, two sets of non-convex constraints including nonlinear spacecraft dynamic model and pointing constraints have been also investigated in this section. In Section 3, decentralized spacecraft formation flying attitude control architecture has been stated. Discrete time local convex optimal controller is designed in Section 4 and the stability and convergence analysis of whole structure are presented in Section 5. Finally, a numerical simulation has been performed in Section 6 to show the effectiveness of the structure.

2. Problem statement

2.1.Mathematical description of spacecraft nonlinear kinematic and dynamic model

where uis the control input torque,Jis inertia tensor matrix,ωis the angular velocity associated with the ispacecraft relative to the inertial frame, tis initial time of the mission, and qis the unit quaternion representing the attitude of the rigid body frame with respect to inertial frame.

2.2. Pointing constraints

In the following, two specific pointing constraints considered in this paper are discussed. In this regard, star trackers field of view must be kept away from sun light. In addition to this pointing constraint, other spacecraft thruster’s illumination should also be prevented from entering the star tracker’s field of view.

As shown in Fig. 1,in mathematical term, suppose that vis the heading unit vector of the ispacecraft sensitive instrument described in its body coordinate frame, w describes the direction of the sun vector in inertial frame, and his the definition of direction vector of the nthruster of the jspacecraft in its body coordinate frame. We denote Has the representation of hin inertial coordination frame.We require that

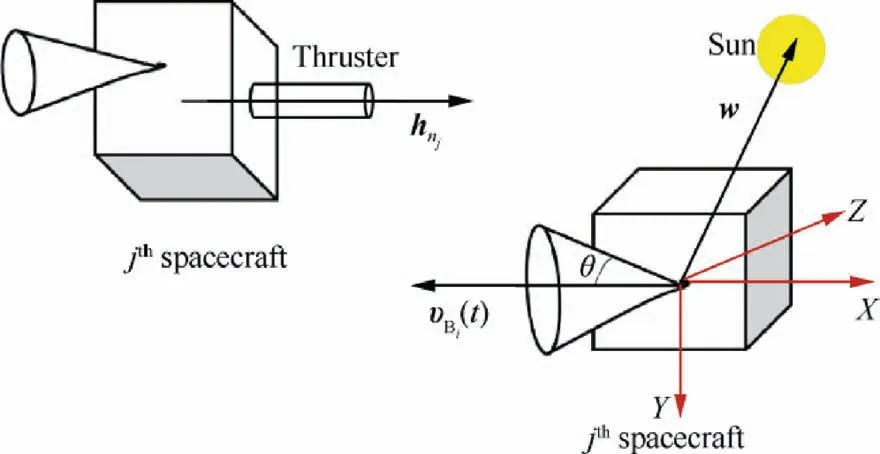
Fig. 1 Sun light (w)/the jth spacecraft thruster (hnj) forbidden pointing constraint for the ith spacecraft.

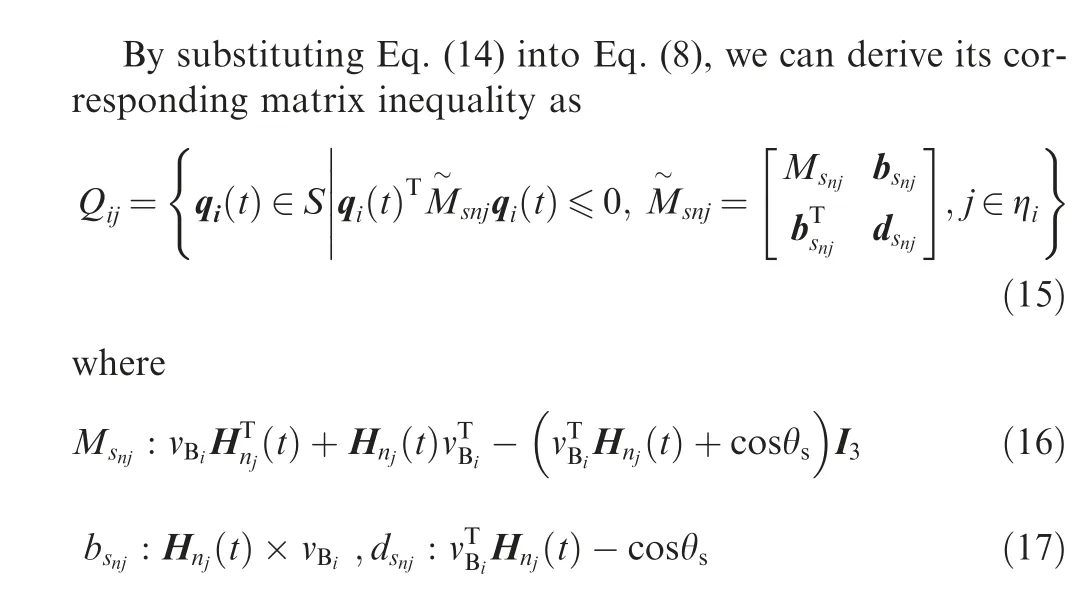
2.3. Boundary constraints

The control torque in each spacecraft is bounded and must satisfy the following boundary constraints during an attitude maneuver.

3. Proposed solution

In this section,a solution is developed to the problem stated in Section 2.We aim to design a formation flying attitude control architecture to acquire the aforementioned goals. The proposed solution involves 4 steps:

Step 1. Decentralized virtual structure formation attitude controller has been designed to generate a series of path nodes toward desired attitude.

Step 2. Discrete nonlinear models of spacecraft attitude dynamic and kinematics using the Euler’s first-order discretization method are developed.

Step 3. The constraint sets represented by Eqs. (10) and (15)are not generally convex.An intrinsic property of the attitude parameterization via quaternion is utilized to make them convex.

Step 4. Local controller based on discrete time convex optimization algorithm is developed to track the desired path subject to constraints Eqs. (10)-(18) within predefined appropriate bound of error.

3.1. Decentralized virtual structure formation attitude control

In this framework, the desired formation of N agents can be treated as a single structure called virtual structure. The associated coordinate frame of this structure is located at its center,called virtual center that has its own specific states.Each member is considered as a node in this structure. The idea behind the virtual structure approach is to set the virtual center’s states as a reference for the whole group to determine each member’s desired states.

As shown in Fig. 2, three different coordinate frames are used. Spacecraft’s body coordinate frame is denoted by C.The inertial coordinate frame denoted by Cis used as a reference frame. The third coordinate frame is the main virtual structure frame called virtual center coordinate frame, C. In a decentralized scheme,every agent can instantiate a local copy of the virtual center frame which has been named as C. The rotation transformation between Cand Cis represented by quaternion q.Therefore,decentralized virtual structure attitude control algorithm is proposed as follows:

Step 1. Set up an initial condition for the attitude of Cwith respect to inertial frame.

Step 2. Apply an appropriate virtual torque to rotate the frame Ctoward its desired attitude with respect to CO.

Step 3. After instantiation of the virtual center states, compute desired attitude for Cwith respect to Cas follows:

Fig. 2 shows the implementation of these steps on the attitude reorientation of 3 spacecraft from their initial attitude toward desired attitude. Three instantiated virtual center frames, C，i=1，2，3 obtain an identical attitude at twhich lead to desired relative attitude between the spacecraft.

Due to the member’s different initial conditions, their corresponding Chas different initial attitude conditions with each other.The formation goals will be achieved if the attitude states of Cbecome identical. Employing proposed virtual torque in Eq. (20) seeks this goal. The first two terms guide the states toward desired attitude while the other terms reduce formation relative state error.Therefore, every agent needs the attitude information of its neighbors to compute suitable virtual torque. We denote this information as φ.

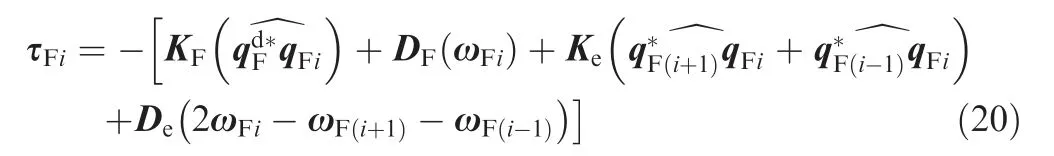
where K，K，D，Dare controller parameters and must be selected positive definite matrices, and φ=［q，ω］ is named as coordination vector. Here, we assume that φ=φand φ=φ. Also φ=［q，ω］ is the virtual structure desired state determined by mission’s goals.

3.2.Discrete nonlinear model of spacecraft attitude dynamic and kinematic

The kinematic and dynamic equations of spacecraft are nonlinear and non-convex.By using Euler’s first-order approximation, we have

where

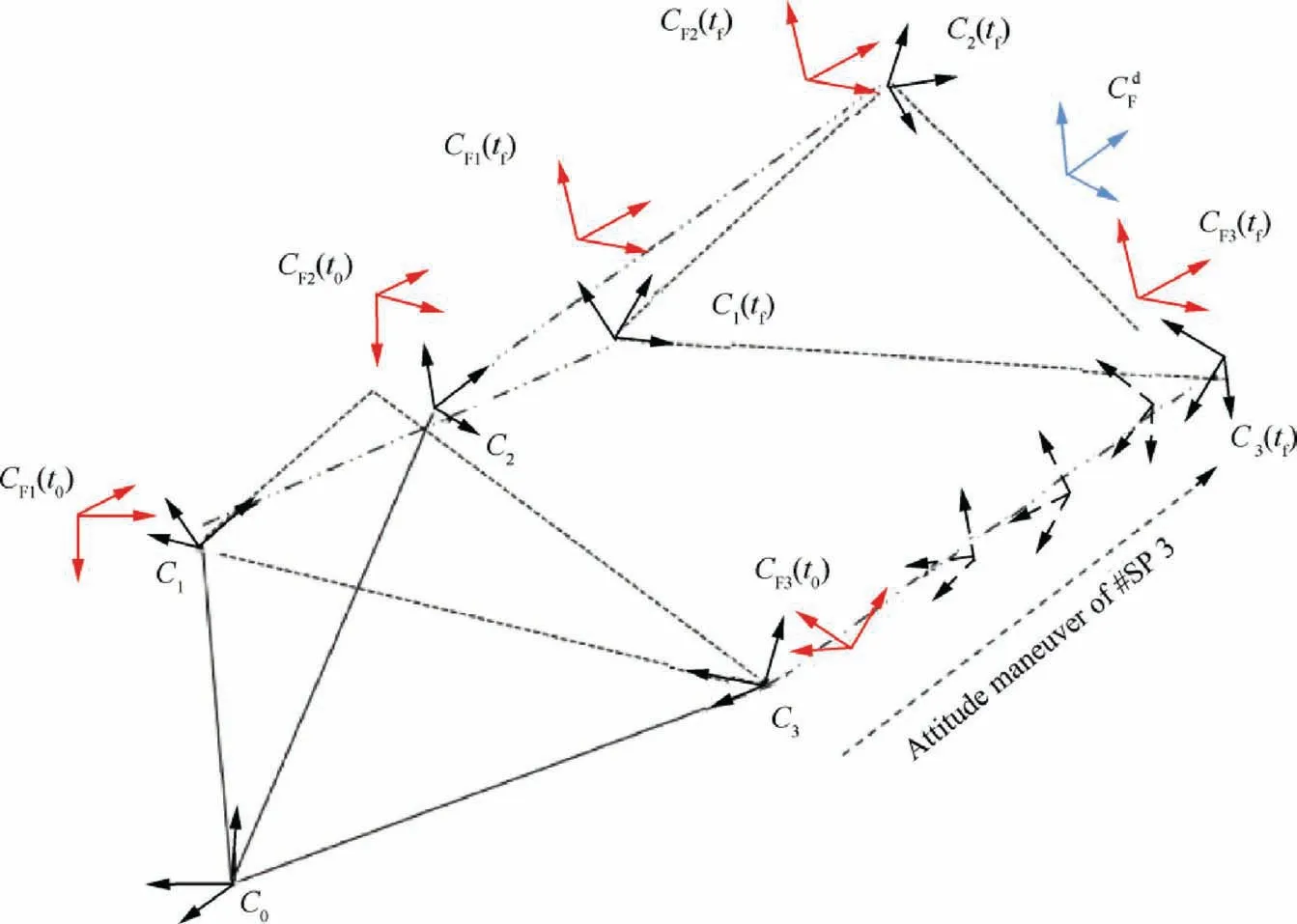
Fig. 2 Decentralize virtual structure multiple spacecraft attitude reorientation path planning.

This approximation with proper sample time converts the nonlinear dynamic equality constraint to convex form.

3.3. Convex form of attitude state constraints

The matrix Ain Eq. (10) is symmetric and has a real set of sign-indefinite eigenvalues,which makes the quadratic inequality, Eq. (10), non-convex. An alternative parameterization of Eq.(10) in term of convex constraint form has been presented in the following. Since q is unity norm, one can write Eq. (10)as

where Eq. (31) is a convex inequality constraint.

3.4. Proposed formation flying control structure

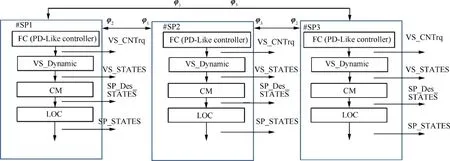
Fig. 3 Block diagram of formation control of a group of three neighbor spacecraft with decentralized virtual structure approach.

Fig. 3 summarizes our proposed formation flying control architecture.In this block diagram,FC,VS_Dynamic,CM,LOC represent formation controller, virtual structure dynamic, control mapper and local optimal controller respectively. Also,VS_CNTrq, VS_STATES, SP_Des_STATES, SP_STATES denote virtual structure control torque, virtual structure states,spacecraft desired states and spacecraft actual states respectively.After calculation of desired states by Eq. (19), a local controller generates necessary control torques by solving a convex constraint optimization problem. This algorithm is discussed in detail in the following section.

4. Local controller based on convex optimization

In this section, a new optimal local controller based on discrete-time constraint convex optimizer is introduced to generate a control torque by each spacecraft to track the associated desired path. Problem 1 shows our proposed optimization problem. In this regard, the cost function is designed based on the error variable consisting of quaternion error norm.This function is supposed to be minimized subject constraints discussed in Section 2.

To find a suitable control torque, at each time instant,Problem 1 is solved based on the argument x(k )={q(k+2)，ω(k+1)，u(k)}.

Assumption 1 is crucial for satisfying the constraints regarding pointing avoidance between neighboring agents.We assume that the above information is always available and accurate and can be exchanged between the neighboring agents without delay.

Fig.4 depicts the procedural regimes among a formation of 3 spacecraft.The design procedure is considered to be sequential, which means that the agents solve their individual problem and calculate necessary control torque one after another.The constraint sets Q，Q, update at every sampling time in which agent i solves its own optimization local controller problem. The solution to Problem 1 at time tprovides an optimal control input, denoted by u(k). This control input is then applied to the system until the next sampling instant t.

In the next section, we will discuss the stability of the proposed structure and its ability to handle different constraints in a spacecraft formation flying missions.

5. Convergence analysis

Referring to Fig. 3, convergence analysis can be decomposed into two separate steps due to the following theorem. First,regardless of local optimal controller tracking performance,asymptotic convergence of the coordination vector(φ)instantiated in each spacecraft formation controller has been proved.Next,the convergence and stability of local controller tracking error within predefined bound have been proved.

Theorem 1. By considering coordination vector dynamic and kinematic such as Eqs. (4)-(6) and the ring communication topology between the formation members and by utilizing the proposed control torque in Eq. (20), if the matrixes K,K，D，Dare selected positive and bounded, then all φ(t)globally asymptotically converge to desired coordination vector φ=［q，ω］ regardless of local controller tracking performance.

Proof. The proof is based on the Lyapunov theorem.Consider the Lyapunov function candidate as

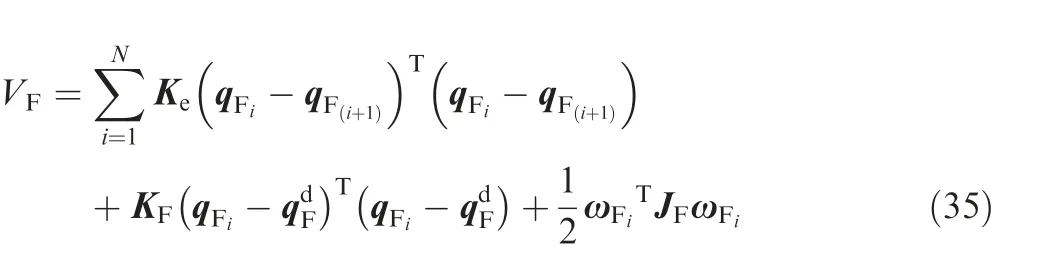
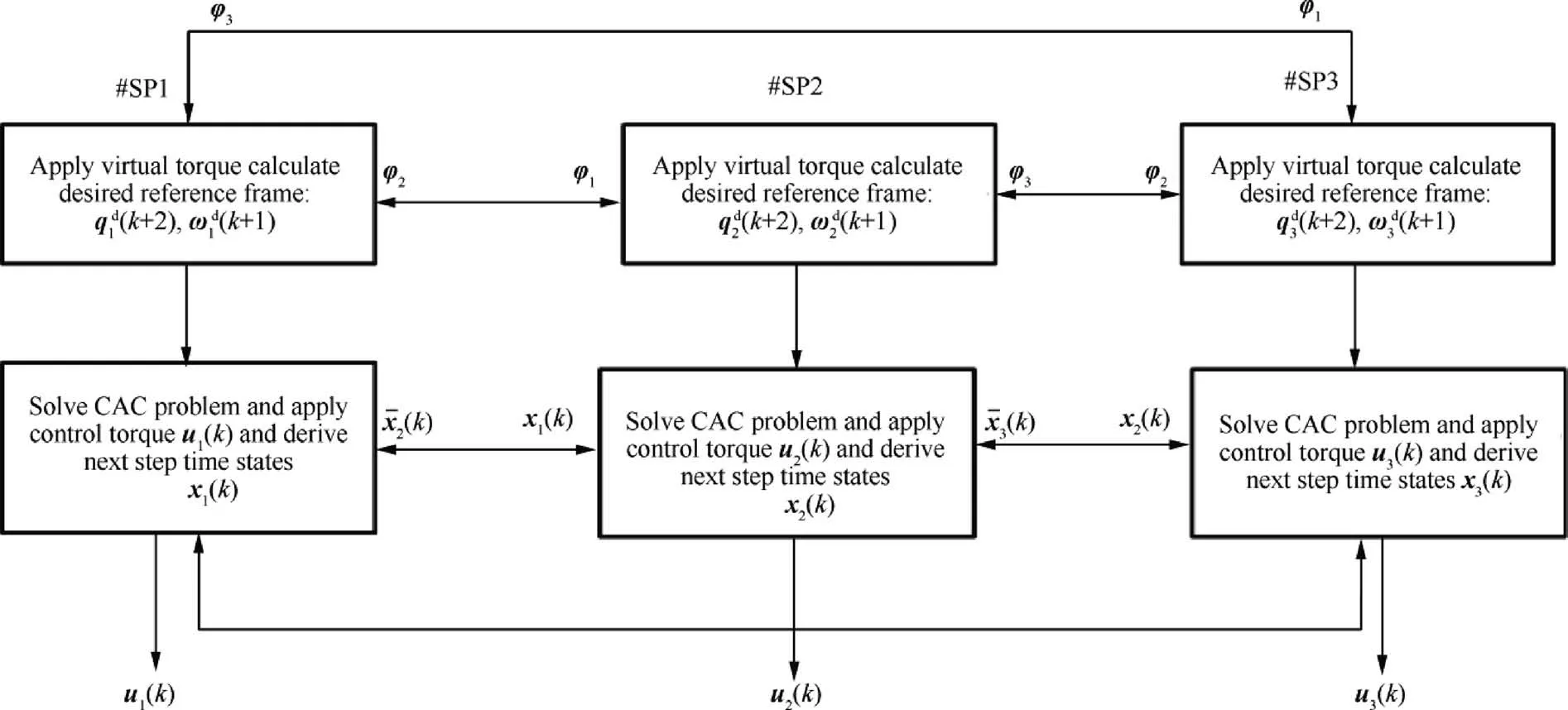
Fig. 4 State flowchart of 3 spacecraft in proposed formation flying control structure.

We use sampling arguments to interpret Problem 1 as a sequence of time invariant problems. When sampling period h:=t-tcan be chosen arbitrarily small,an arbitrary accuracy may be achieved when approximating Problem 1 with Problem 2.

Notation:the gradient of the function f(x，t)with respect to x at the point (x，t) is denoted as ∇f(x，t)∈R,while the partial derivative of the same function with respect to t at(x，t)is written as ∇f(x，t)∈R. Similarly, the notation∇f(x，t)∈Rdenotes the Hessian of f(x，t) w.r.t the time t at (x，t),whereas ∇f(x，t)∈Rdenotes the partial derivative of the gradient of f(x，t) w.r.t the time t at (x，t). The tensor∇f(x，t)∈Rindicates the third derivative of f(x，t) w.r.t the time t at (x，t). The matrix ∇f(x，t)=∇f(x，t)∈Rindicates the time derivative of the Hessian of f(x，t) w.r.t the time t at(x，t),and the vector ∇f(x，t)∈Rindicates the second derivative in time of the gradient of f(x，t)w.r.t the time t at (x，t). The indicator function is indicated as ς(x)for the convex set ⊆R; by definition ς(x )=0 when x ∈X and ∞otherwise. The subdifferential of ςis the set-valued map known as normal cone N:R⇉R.

Assumption 2. The function f(x;t) is twice differentiable and strongly m convex in x ∈X and uniformly in t. That is the Hessian of f(x;t)with respect to x that is bounded below by m for all ∈X. In other words,

Assumption 2. The initial states x(t) and final desired states x(t) for all spacecraft body coordinate frame are strictly feasible point of Problem 2. i.e. (t)∈X,x(t)∈X.

Assumption 2 is based on the idea that initial state of spacecraft can be selected in a feasible region of Problem 2, where their sensitive instruments do not face bright objects. Also,final desired states which are determined by the mission requirements can be defined in a condition where the forbidden attitude constraints are satisfied.

Remark. Due to Lyapunov theorem in Ref. [28], the desired path,x， is not necessarily generated in the feasible domain at each time instant, so the tracking Problem 2 cannot reach the solution x(t)=x(t). However, there will be a sequence of answers ^x(t) in X where its members are the solution of problem bellow at each sample time:

Proof. Since the virtual structure controller is globally asymptotically stable and also the initial and final desired states are in feasible set of Problem 2, the generated path for each spacecraft at each time instant has a bounded distance from a convex feasible set of optimal problem.This property and Lemma 2 guarantee the overall system stability of tracking error and the whole system states.

6. Numerical simulation

In this section, a numerical simulation will be carried out to show the capability of the proposed formation flying control structure in the presence of static state and dynamic (relative state)forbidden constraint.Here,as a novel approach,formation flying of 3 spacecraft has been utilized to overcome the difficulty of stereo cross-track imaging multiple sequential time limited maneuvers. In this venue, spacecraft do not need to perform fast slew maneuvers with large level of actuation torque.

We consider that a group of three spacecraft tend to reorient their attitudes toward desired formation to accomplish a stereo cross-track imaging mission, as shown in Fig. 5.

Here,we assume that each spacecraft has 2 thrusters incorporate with reaction wheels to perform the desired maneuvers.Spacecraft 1 and 2 have been considered as a neighbor where their thrusters sparkle and pollution can affect each other.Moreover, the ring topology connection between the formation members has been established.

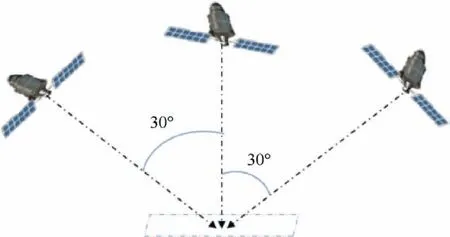
Fig.5 Desired relative attitude of 3 spacecraft to perform stereo imaging.

The moment of inertia matrix and sensitive star tracker’s alignment vector in the body coordinate frame for each spacecraft are diag(［4，4，2］)kg·mand v=［0，0，-1］respectively.The attitude control subsystem technical requirement specification for mission accomplishment has been gathered in Table 1.These requirements include desired attitude of each spacecraft body frame with respect to the virtual center frame in term of Euler angle,terminal desired states of virtual center frame with respect to inertial frame, and the initial states of each spacecraft body frame. The alignment vectors of each spacecraft’s thruster’s axis and the mission constraints including angle of forbidden cone around each spacecraft’s star tracker and the upper bound of control torques thresholds are gathered in Table 2.

According to Eq.(49),the sampling period that guarantees an upper error bound of 10with 2 iterations of prediction and correction steps needs to be chosen as h＜0.2 s. Here we select 0.1 for the time step of the local controller algorithm.Therefore, we set the virtual structure control parameters and local optimal prediction and correction steps as in Tables 3 and 4.

Fig. 6 shows that the decentralized virtual structure approach is able to successfully generate the path nodes toward desired attitude for each spacecraft. Meanwhile, eachlocal optimal controller has generated appropriate control torque to track its associated path.

Table 1 Desired and initial attitude states of spacecraft formation.

Table 2 Spacecraft thruster’s alignment vectors and constraint thresholds.

Table 3 Formation controller design parameters.

Table 4 Local controller prediction and correction algorithm parameters.

Fig.7 shows the angle between the sensitive instrument vector and the sun light vector. The angles are larger than the aforementioned thresholds expressed in Table 3 which means that the sun prevented from entering the star trackers field of view.

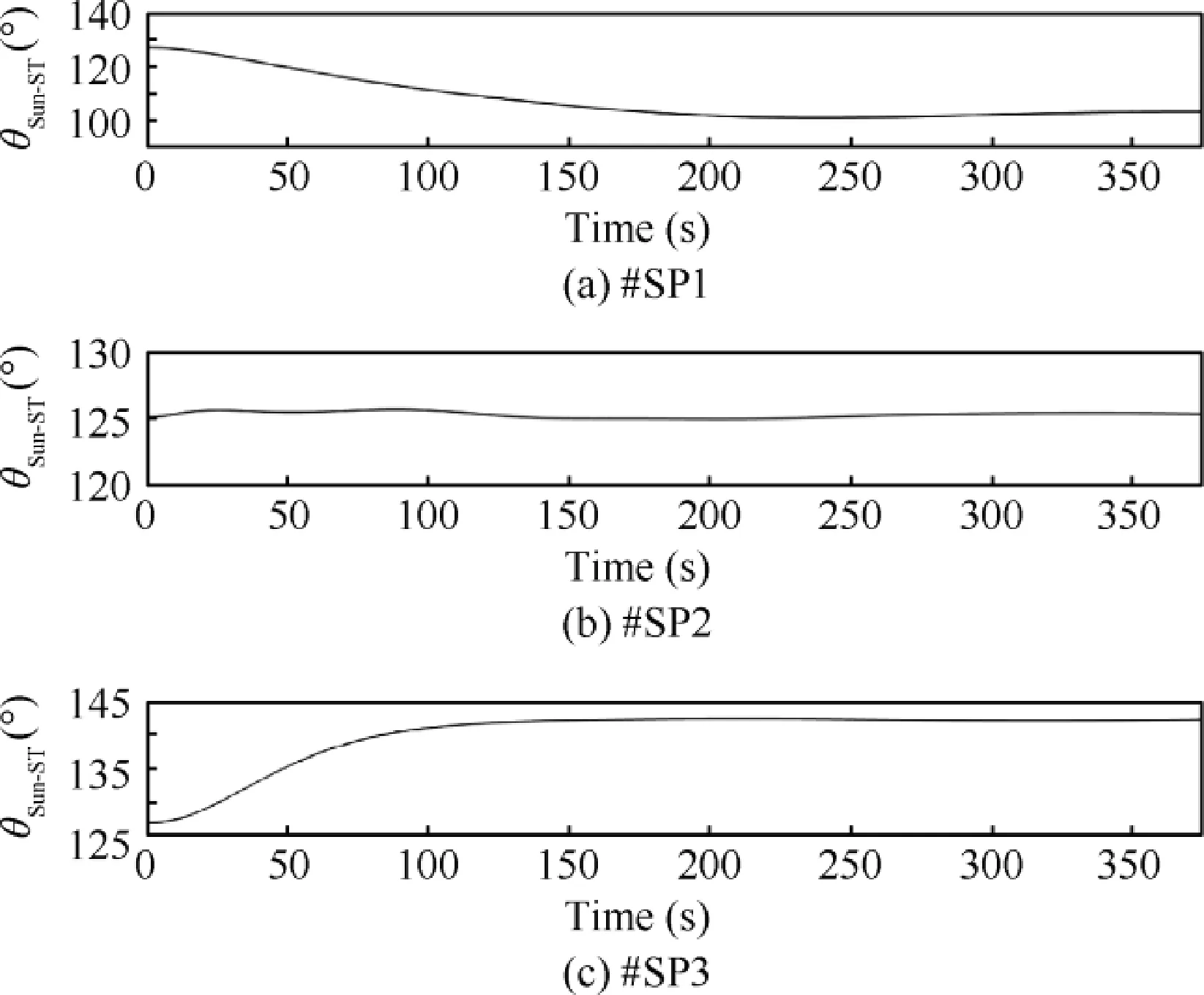
Fig. 7 Angle between star tracker of all spacecraft and sun vector.

Fig. 6 Desired attitude and actual attitudes of 3 spacecraft.

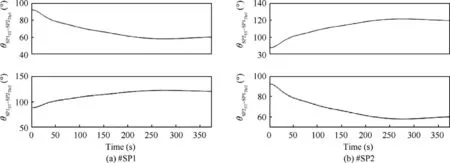
Fig. 8 Angle between star tracker of spacecraft 1, 2 and 2 thrusters of neighbor.

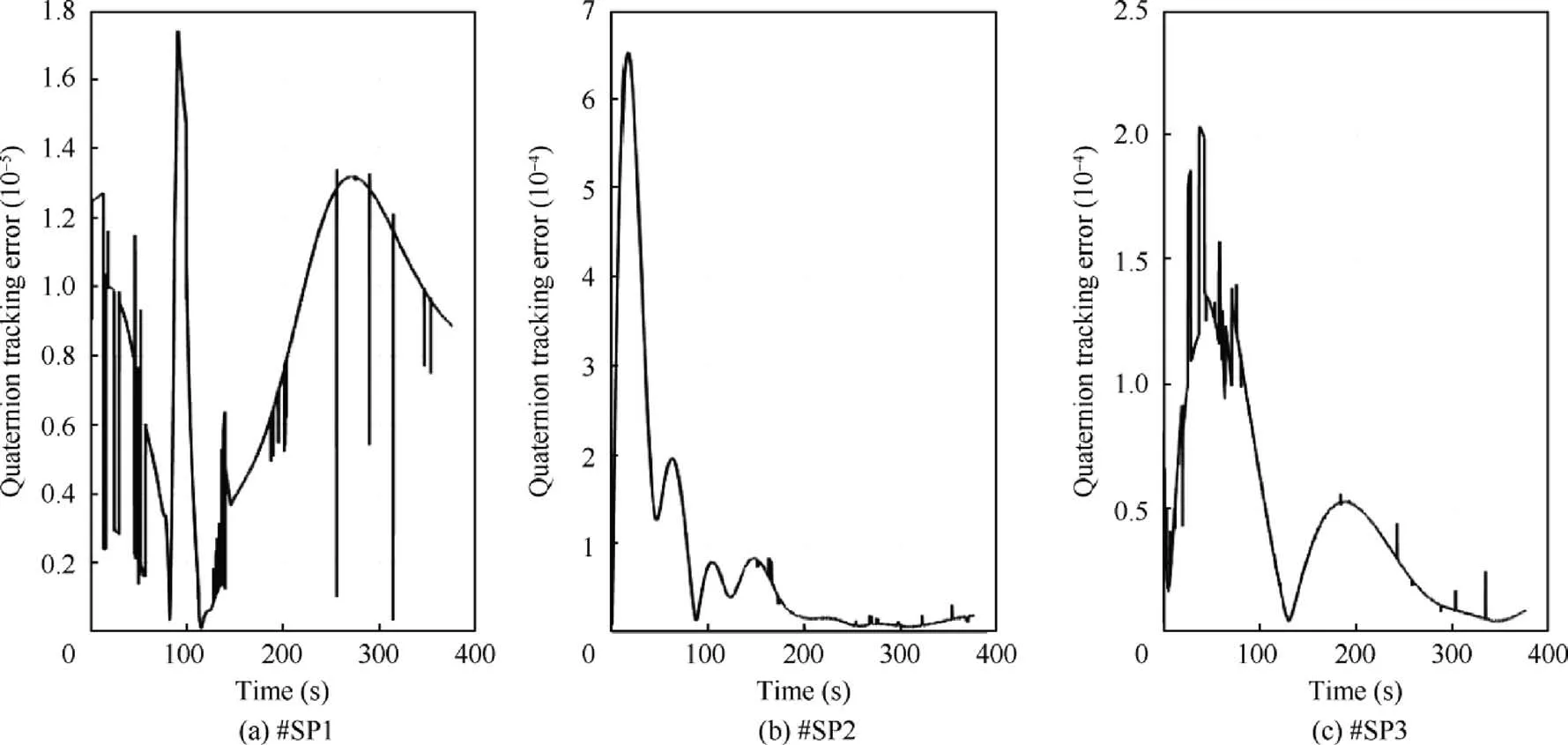
Fig. 9 Desired set point quaternion tracking error.

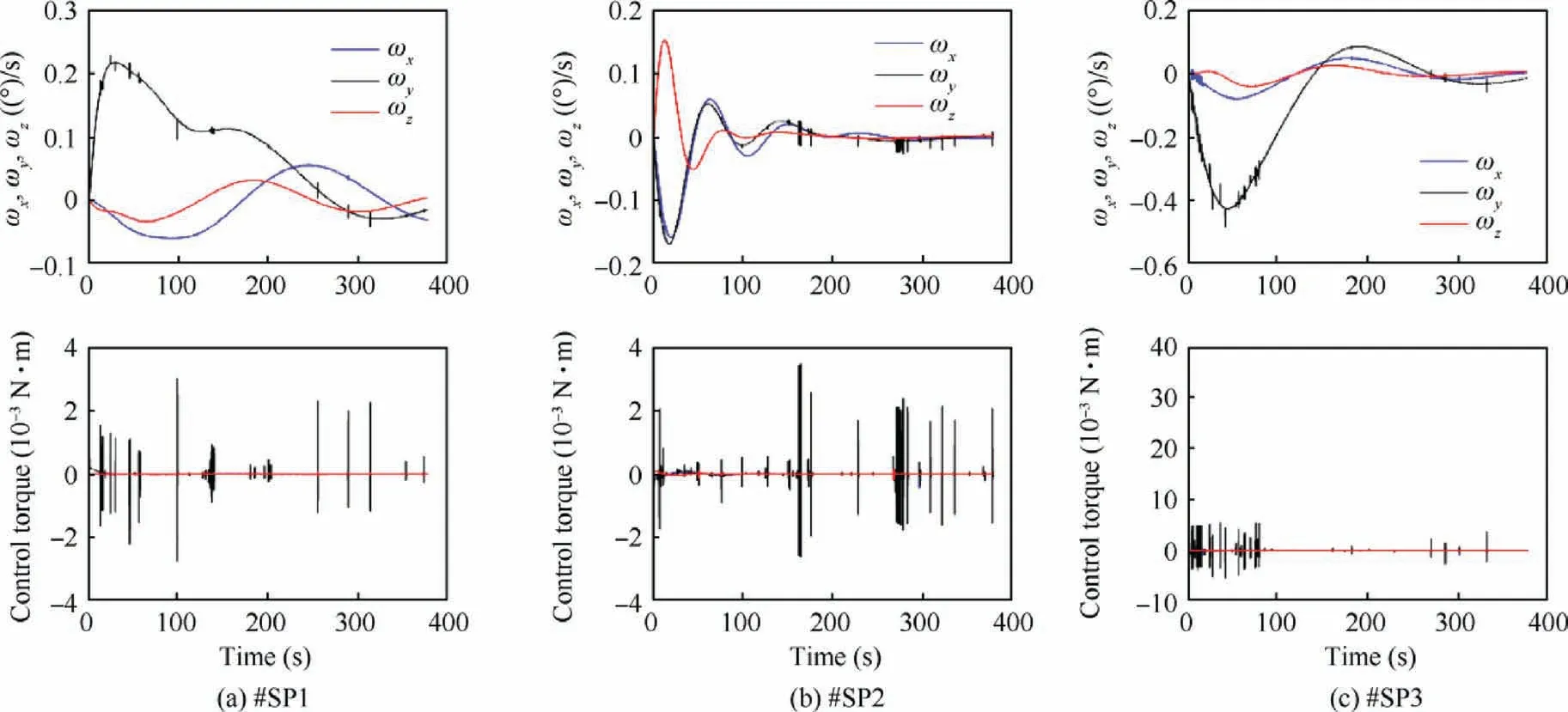
Fig. 10 Angular velocity and control torque of 3 spacecraft.

7. Conclusions

This investigation was carried out on discrete-time attitude control of the formation flying of a group of spacecraft in presence of multiple static and relative constraints.A combination of decentralized virtual structure formation attitude controller and optimal local controller has been designed to overcome these constraints.An innovative upper bound on discrete sample time of local optimal controller implementation has been calculated to acquire the mission goals within an acceptable error bound. The advantages of the proposed structure have been shown in performing a stereo imaging scenario. The results show that the proposed algorithm can accomplish the mission within spacecraft lower level of necessary actuations and slew rates. Moreover, it could satisfy the forbidden attitude constraints.

Regarding areas for future improvement, we would like to point out that in this investigation we consider the exact model of spacecraft dynamic equation. However in reality, some of the spacecraft parameters such as the moment of inertia matrix include uncertainties which can cause the inappropriate disturbance torques on the attitude dynamic model. In future work,it is appropriate to design a new control structure to reduce the undesirable effects of disturbances. Also, considering other attitude constraints such as keeping the sun in the field of view of sun sensors in a formation flying mission could make the algorithm more applicable.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.