LEO navigation augmentation constellation design with the multi-objective optimization approaches

Yi HAN, Lei WANG,b,*, Wenju FU, Hito ZHOU, To LI, Beizhen XU,Ruizhi CHEN,b

a State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China

b Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China

KEYWORDS LEO-augmented multi-GNSS;LEO constellation design;MOPSO;Multi-objective optimization;Orbit optimization

Abstract Low Earth Orbit (LEO) satellite for navigation augmentation applications can significantly reduce the precise positioning convergence time and attract increasing attention recently.A few LEO Navigation Augmentation (LEO-NA) constellations have been proposed, while corresponding constellation design methodologies have not been systematically studied. The LEO-NA constellation generally consists of a huge number of LEO satellites and it strives for multiple optimization purposes.It is essentially different from the communication constellation or earth observing constellation design problem. In this study, we modeled the LEO-NA constellation design problem as a multi-objective optimization problem and solve this problem with the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm. Three objectives are used to strive for the best tradeoff between the augmentation performance and deployment efficiency, namely the Position Dilution of Precision (PDOP), visible LEO satellites and the orbit altitude. A fuzzy set approach is used to select the final constellation from a set of Pareto optimal solutions given by the MOPSO algorithm. To evaluate the performance of the optimized constellation, we tested two constellations with 144 and 288 satellites and each constellation has three optimization schemes: the polar constellation, the single-layer constellation and the two-layer constellation.The results indicate that the optimized two-layer constellation achieves the best global coverage and is followed by the single-layer constellation. The MOPSO algorithm can help to improve the constellation design and is suitable for solving the LEO-NA constellation design problem.

1. Introduction

The Low Earth Orbiters (LEO) constellations have become increasingly popular in recent years. Several ambitious commercial LEO communication constellations, such as OneWeb,SpaceX,and Boeing,has planned to launch hundreds or thousands of LEO satellites to provide worldwide internet access soon.The navigation applications of LEO in navigation also draw numerous attention. The Stanford researcher examined the potential benefit of navigation using commercial communication LEO constellation.Although these brand-new constellations were proposed to meet the rising desire for broadband communication, it is highly potential that they can also serve as navigation systems. The Iridium NEXT constellation has announced its ‘Satellite Timing and Location’(STL) service, which provides 20-50 m positioning accuracy and better than 200 ns timing accuracy.The Iridium NEXT constellation is served as the backup navigation technique to improve the navigation service resilience. Recent research has revealed a few benefits of LEO based navigation: (A) the fast change of LEO satellite geometry can dramatically reduce the Precise Point Positioning(PPP)convergence time.Current Global Navigation Satellite System (GNSS) PPP techniques require 30-40 minutes to converge to centimeter accuracy which is unacceptable for most applications. By introducing the LEO constellation, the convergence time hopefully can be reduced to a few minutes, which potentially brings revolutionary progress in GNSS precise positioning communities.(B) The ranging signals from the LEO satellite have a shorter propagation path,which leads to less signal power loss.Therefore, the satellite becomes less power consuming and the LEO navigation receivers hopefully can track stronger navigation signals, which is beneficial for anti-jamming. Wuhan University has launched its scientific experimental satellite named‘Luojia-1A’has demonstrated the initial capacity of navigation augmentation from the LEO satellite.Table 1 summarizes some LEO constellations that have been deployed or proposed.

With the LEO Navigation Augmentation (LEO-NA) concept being recognized, a few constellations have the plan to support the LEO-NA functions, such as the Chinese ‘Hongyan’ constellation.However, there are a few challenges for deploying the LEO-NA constellations since the constellation design is one of the most important topics.A well-design constellation can improve the LEO-NA performance and reduce the constellation deployment cost, while this problem has rarely been seriously studied. A few simulative research had explored the benefit of LEO-NA with the Iridium constellations or the other polar constellations, which may not be the best choice for the LEO-NA constellation.

There have been a few research that looked into the constellation design problem,such as the exhaustive enumeration algorithm and the Evolutionary Algorithms (EAs), but most of them are based on the Single-objective Optimization Problem (SOP).Budianto and Oldsused a combination of exhaustive grid search and heuristics in optimizing the orbit parameters.Casanova et al.employ the EAs to find the optimal Geometry Dilution of Precision(GDOP)flower constellation. Although the EAs has been proven to be more efficient than the exhaustive enumeration algorithm, it is only capable of handling the single optimization problem. Besides, some constellations based on single-objective optimization approaches have been applied in the earth-observing constellation optimization problem, such as the GNSS Radio Occultation (RO)and GNSS Reflectometry constellations.In aeronautical and aerospace engineering,the optimization algorithms have also been successfully applied to search optimal parameters.

The LEO-NA constellation design should be a multiobjective optimization problem since the navigation performance cannot be measured from a single aspect. We need to consider the positioning accuracy,continuity,etc.when evaluating the navigation constellation performance.Regarding the multi-objective optimization, the Multi-Objective Evolutionary Algorithms(MOEAs)have been widely used in aeronautical and aerospace engineering.Meanwhile, the optimum constellation has been resolved for various missions based on different objectives by MOEAs. Besides, the Non-dominated Sorting Genetic Algorithm (NSGA),the improved nondominated sorting genetic algorithm (NSGA II) algorithm,Pareto Archived Evolution Strategy (PAES),etc. also become optional algorithms to solve the multi-objective optimization problem. Unfortunately, the LEO-NA constellation design problem has not attracted enough attention, but itwould become increasingly important as the LEO constellation development.

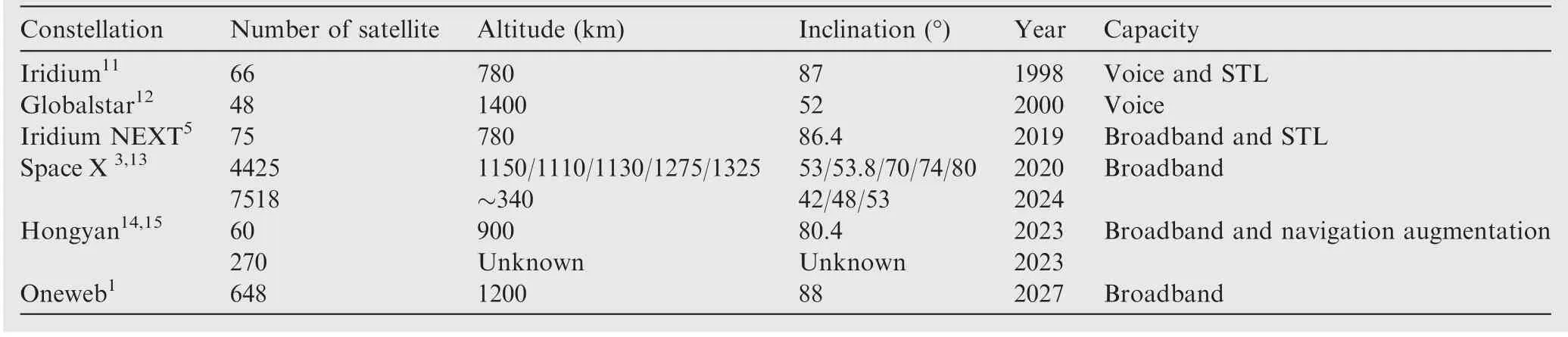
Table 1 Summary of some LEO constellations that have been deployed or proposed.

In this study, we attempt to model the LEO-NA constellation as a Multi-objective Optimization Problem (MOP)according to the performance and the cost criteria, and then solve this problem with the Multi-Objective Particle Swarm Optimization(MOPSO)algorithm.After comparing three different constellation designs,we find that a two-layer constellation optimization outperforms the single-layer constellation and thus is more suitable for the LEO-NA constellation. The remaining of the paper is organized as follows:Section 2 introduces how to model the LEO-NA constellation optimization problem into a MOP. Section 3 introduces how to solving the MOP with the MOPSO algorithm. Sections 4 and 5 introduce the experiment setup and experiment results. Section 6 summarizes the conclusions.

2. Modeling LEO-NA constellation optimization problem

The earth observing and communication constellation optimization problem has been extensively studied. The LEONA design is an emerging LEO application and its constellation design has not been fully understood. The first challenge of the LEO-NA constellation design problem is modeling the constellation design problem into a Multi-objective Optimization Problem (MOP) according to the target and constraints.In this study, we assume the total satellite number in the constellation is fixed,then strive for the optimal constellation configuration to improve the augmentation performance.

2.1. Optimization target of LEO-NA constellation

The LEO-NA constellation is built as an augmentation system of the existing Medium Earth Orbiters (MEO), Geosynchronized Earth Orbiters (GEO) and Inclined Geosynchronized Earth Orbiters (IGSO) based GNSS. These LEO constellations are designed for transmitting the ranging signals to the ground users for enhancing their navigation and positioning performance.The existing GNSS constellation can provide continuous,real-time,and accurate positions most time, but they also confront a few challenges: (A) Vulnerability; (B) Long convergence time for the precise positioning (C)Poor availability in a complex environment. The LEO-NA constellation is expecting to broadcast stronger signals for solving the vulnerability issue.The rapid change of the relative geometry between the LEO satellite and the ground users can significantly reduce the convergence time. The LEO-NA system can also serve as an independent satellite navigation system to improve service availability. Therefore, the LEO-NA constellation should be designed to maximize its efficiency from these aspects.

2.2. Performance indicators of LEO-NA constellation

To achieve the constellation optimization, the overall optimization target should be translated into measurable performance indicators, so that we can translate the constellation design problem into an optimization problem.At first,the vulnerability of GNSS is mainly caused by weak signal power.According to the Friis signal propagation equation:

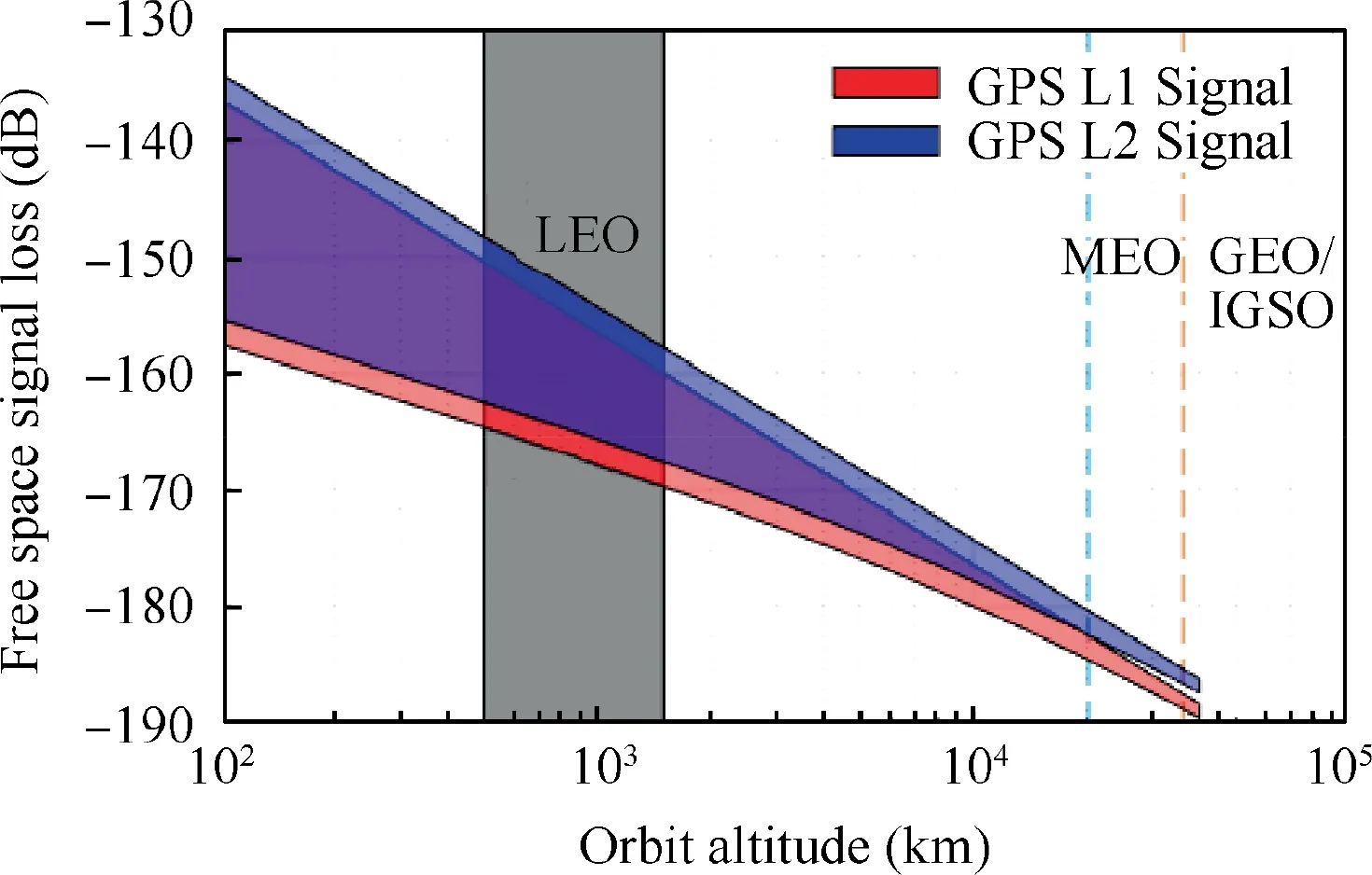
Fig. 1 Relationship between orbit altitude and free space signal loss.

where Pand Pare the signal power of transmitted and received. Gand Gare the gain of transmitting antenna and receiving antenna respectively.λ and d are the signal wavelength and signal propagation distance.According to the equation, it can be concluded that the received signal power is inversely correlated to the signal propagation path, which means that the lower orbit altitude causes smaller signal power loss.The free space signal loss of GNSS signals is illustrated in Fig. 1. The figure indicates that the navigation signal power loss varies according to different elevation angles for the same orbit altitude case. The LEO satellite at 500 km altitude can save up to 30 dB free space loss comparing to the MEO satellites. The lower orbit altitude means less signal power loss, so the satellite is more energy efficient.

Another concern of the satellite altitude is the constellation deployment cost. There is a common sense that lower orbital altitude leads to lower deployment costs.The LEO constellation with lower orbital altitude has many other merits,such as lower propagation latency, low emission cost, and strong system survivability. Hence, the orbit altitude should be considered as a major objective and lower orbit altitude should strive for signal strength and deployment cost consideration.

Secondly, the long convergence time of Precise Point Positioning (PPP) with the current GNSS system is caused by the slow variation of geometry.In PPP,the user position parameters are strongly correlated to other parameters. The position parameters can be precisely estimated until the satellite geometry changed significantly, which takes a long time for the existing GNSS constellation since a single MEO satellite pass takes about 6 hours. The LEO satellite achieves fast geometry change thus can reduce the PPP convergence time. There is a few simulative research confirms that the LEO satellite can dramatically reduce the PPP convergence time.An example of the relationship between the visible LEO number and the convergence time is illustrated in Fig.2.Although the detailed convergence time depends on the satellite configuration, the figure has revealed the rough relationship between the visible satellite number and the PPP convergence time. The figure indicates that more visible LEO satellites can further reduce the PPP convergence time.Therefore,users need a more visible LEO satellite number to reduce the convergence time. Meanwhile, the visible LEO satellite number depends on the total satellite number,orbit altitude,and the signal beam width,etc.

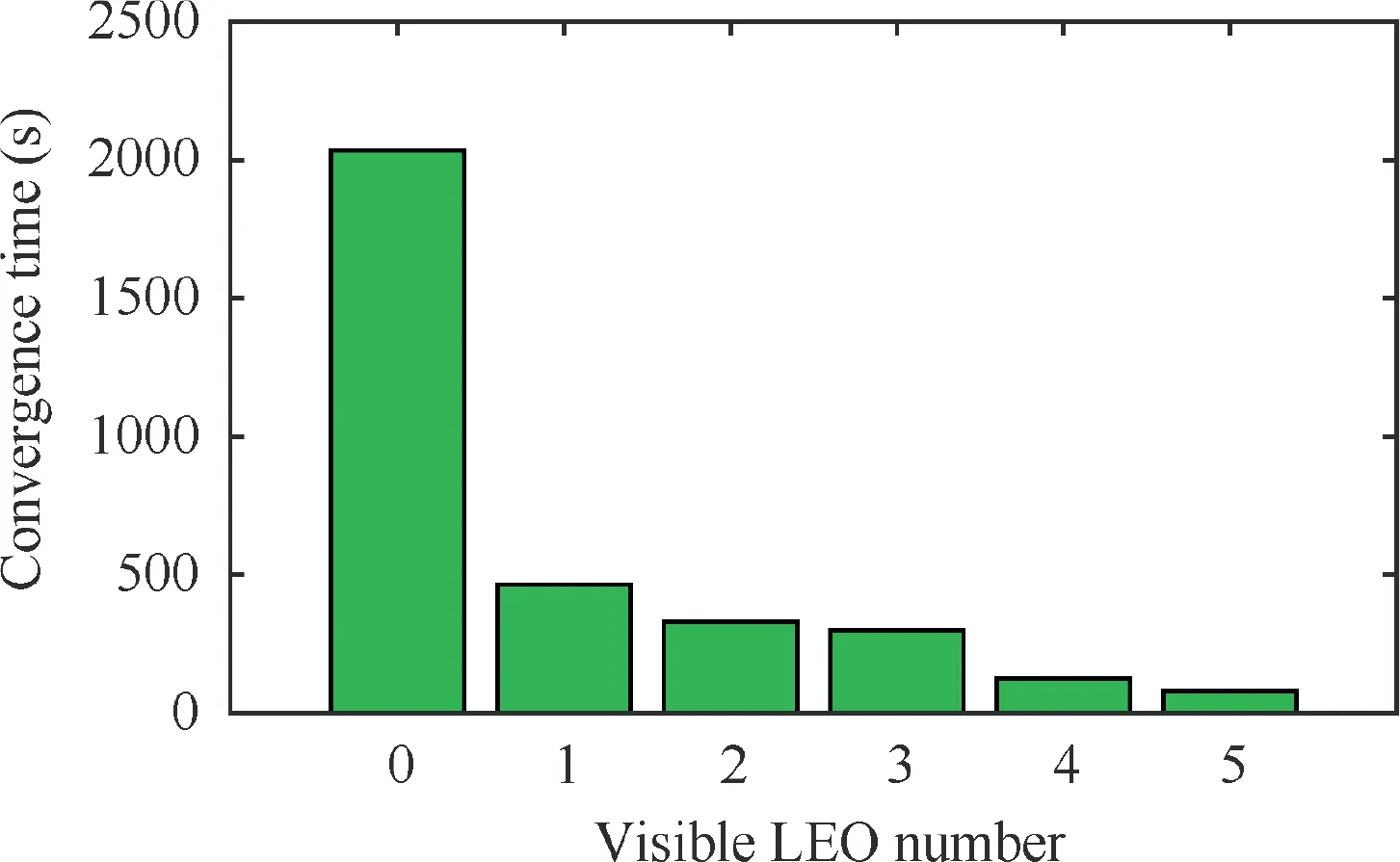
Fig. 2 An example of the relationship between the visible LEO number and PPP convergence time.

Thirdly, the improvement of the availability in a challenging environment can be measured by the Dilution of Precision(DOP). The DOP value is a measure of the satellite geometry impact on the positioning accuracy.The user positioning accuracy can be roughly evaluated with:

where Pis the pseudorange measurement on ith frequency GNSS signals; ρ is the geometrical distance between the satellite and user antenna,which is related to the satellite orbit;c is the speed of light. dtis the satellite clock bias which can be obtained from the broadcast ephemeris; dtis the receiver clock bias to be estimated; Iand T are the ionosphere delay and troposphere delay,which can be corrected with the empirical models. ε is the measurement noise.

In this study, we consider the GPS, GLONASS, Galileo,BeiDou and LEO constellation combined scenario The LEO can also be used to combine with one or more constellations in practice. For the multi-GNSS based standard positioning scenario, the observation equation can be expressed as:

where Q(1，1), Q(2，2), Q(3，3) are the primary diagonal elements of the matrix Q.The PDOP is derived from the Jacobian matrix J, which contains the satellite geometry information.Thus, PDOP is a measure dominated by satellite geometry.If the LEO constellation combined with the existing GNSS constellations achieves good satellite geometry for positioning,it should achieve a small PDOP value.Hence the small PDOP value is considered as the third objective in the constellation design.

These three objectives confront contradictions.Lower orbit altitude refers to smaller service coverage and consequently less visible satellite. Meanwhile, more visible satellites may not always lead to smaller PDOP as well. Hence, these three objectives cannot be optimized at the same time and a proper trade-off should be applied during the constellation design.

2.3. Modeling LEO constellations

The performance indicators should be expressed as a function of constellation parameters in the optimization procedure, so we need to determine the representation of the LEO constellations. The selection of the parameter set depends on the constellation characteristics. There are a few constellations widely used in constellation design,such as the Walker constellations,the Flower constellations,etc. In this study, we employ a two-dimensional Lattice Flower Constellation (2DLFC), which is a more general constellation. The well-known Walker constellation is a special case of the 2D-LFC constellation.A 2D-LFC constellation can be uniquely defined with 9 parameters. The first 6 parameters define the Keplerian elements of the reference satellite, given as the orbit altitude(a),the eccentricity(e),the inclination(i),the argument of perigee(w),the right ascension of ascending node(Ω,RAAN),and the mean anomaly (M). The rest three parameters define the constellations structure, known as the number of orbit planes(N), the number of satellites per orbit (N) and the phasing parameter (N). The phase parameterNdefines the initial distribution of the satellites in the constellation and satisfies N∈［1，N］.The 6 Keplerian elements are real-valued parameters and the three constellation structure parameters are defined as an integer. A 2D-LFC configuration meets the following constraint:

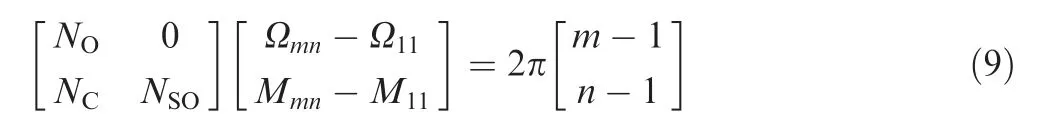
where m denotes the mth orbit, and n denotes the nth satellite in a certain orbit, Ωand Mdenotes the longitude of the ascending node and the mean anomaly of the nth satellite on the mth orbital plane; Ωand Mare the location of the initial satellite. In the optimization, we assume the LEO is in a circular orbit,global service coverage and a fixed total satellite number, and then the constellation can be simplified with the following four parameters. Considering the external constraint, such as the space environment, orbit precession, and satellite life, etc, the four parameters to be optimized should be constrained in a certain range, which is listed in Table 2.

2.4. Formulating multi-objective optimization problem

With the three performance indicators and 2D-LFC pattern identified,the constellation optimization problem can be transformed into a multi-objective optimization problem.

At first, the three performance indicators should be transformed into three objective functions. As known, the impact of the constellation on the user positioning performance varies upon the user’s location and time,hence the reasonable objective function should be formed by fully considering the spatialtemporal properties. In this study, a set of randomly distributed ground stations with global coverage is generated to reflect the spatial impact. the temporal impact is considered by generating a set of epochs covering a repeating period.All the epochs of all these stations form a dataset and the objective function is derived from the simulated data set. In this study, we convert the performance indicators into the three objective functions:

where T is the total number of epochs and t is the epoch index,rdenotes the ith station and is the total station number in the set, FC denotes one of the 2D-LFC configurations, a is the orbit altitude of LEO constellation. The objective function f(FC) indicates that we find the station with maximum mean PDOP value over a period,which corresponds to the worst sta-tion in the data set. The objective function f(FC) means to find the station with the minimum mean visible satellite number, which is also the worst case in terms of visible satellite number. We apply a minus sign is to convert the maximizing problem into a minimizing problem. The third objective f(FC) is to optimize the orbit altitude. According to the requirement analysis in Section 2.2,we simply minimize it during the optimization procedure. For the two-layer constellation optimization problem, we choose to minimize the mean altitude of the two constellations. Then the final goal of the optimization is to minimize f(FC) f(FC) and f(FC) at the same time. The three objective functions mean we attempt to ensure the worst case on earth to ensure the performance of LEO-NA constellation.

Table 2 The variation range of the 2D-LFC constellation parameters in optimization.

With the objective function identified, then we start to formulate the multi-objective optimization problem for the LEONA constellation design problem.For the multi-objective optimization problem with m objective functions, its objective functions f(X)，f(X)，...，f(X) form a vector function f(X)=［f(X)，f(X)，...，f(X)］. The vector X is the parameter set to be optimized. Without loss of generality, we assume there are a few constraints applied to the parameter set X.As a result, the Multi-objective Optimization Problem(MOP) can be expressed as:

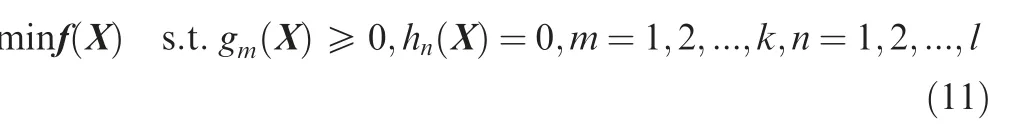
where g(X) and h(X) are the constrained equations of the MOP. For the LEO-NA constellation design problem, the objective function f(X)is given in Eq. (10)and the constrained equation is listed in Table 2.

3. Solving LEO-NA constellation optimization problem

With the LEO-NA constellation design problem converted into a Multi-objective Optimization Problem (MOP), how to solve this problem is discussed in this section.

3.1. Pareto optimal in MOP problem

Comparing to the Single objective Optimization Problem(SOP), the key issue of the MOP problem is how to select the optimization solution when there is a conflict between the objectives.In this study,we follow the Pareto optimal concept during solving the MOP problem.

The first important concept is Pareto dominates, which are used to compare the two solutions in MOP. Given two state vectors Xand X, if the following relationship holds:

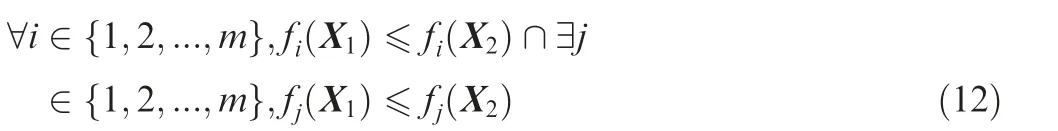
then we called XPareto dominates Xand denoted as X≤X. Pareto dominates means that all the objective function value computed from Xis not worse than that of Xand at least one objective function value Xis better than that of X.

The second concept is the Pareto Optimal. A state vector X∈Ω is Pareto optimal if for every X ∈Ω and A={1，2，...，m} either

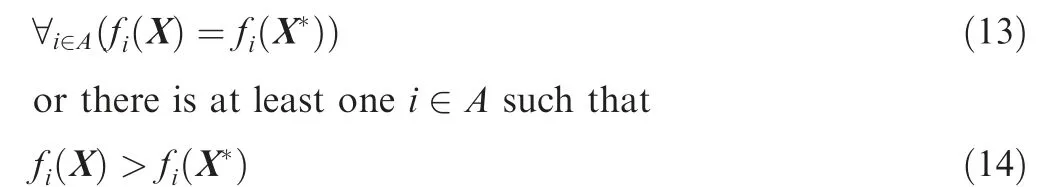
It means that all the objective function values of Xshould not be worse than any of the objective function values computed with the solution set Ω or no Pareto dominant solutions than Xappeared in the set Ω,then Xis a Pareto optimal solution.According to the definition of the Pareto optimal and the Pareto domination, it can be seen that the solution of a MOP should not be a single solution,but a solution set is composed of the Pareto optimal solutions.All the solutions in the Pareto solution set are known as the Pareto front.

The Pareto definitions are general rules for MOP problems,which are independent of the specific optimization algorithm.The goal of the optimization algorithm is to find the Pareto optimal solution set in different ways.

3.2.Optimizing LEO-NA constellation with MOPSO algorithm

There are a few methods to solve the MOP and we adopt the MOPSO algorithm to solve the LEO-NA algorithm design problem since it is easy-to-use and high efficiency.

With the MOP problem clarified, the remaining issue is to find the Pareto optimal solution set with the MOPSO algorithm.The MOPSO algorithms is a kind of evolutionary algorithm, so it finds the solution iteratively. Hence, the algorithm can be understood from three factors: initialization, iteration direction and criteria to terminate the iteration. A flowchart of solving the LEO-NA constellation design problem is illustrated in Fig. 3.In the flowchart, we add an extra step to pick out one constellation as the final solution since the output of MOPSO is a solution set.

The first step of the MOPSO algorithm randomly generates N group of 2D-LFC constellation parameters as the initial seeds.With these constellation parameters, we can compute the orbit of these constellations within a certain period T. To obtain the objective function values,we randomly generate M globally distributed stations and assumes all these stations are capable of tracking GPS, GLONASS, BeiDou and Galileo signals as well as the LEO navigation augmentation signals. Then we set sampling intervals for the stations and obtain an observation dataset with (T/t) samples. Then we compute the mean visible LEO satellite number and mean PDOP over the period T, so that we can compute the objective function value f(FC), f(FC)and f(FC). With these objective function values, we can select the Pareto optimal solutions. For the two-layer constellations,it is more complex in describing the constellation,but it has little impact on the objective function calculation.

The second issue is how to determine the iteration direction to make sure the convergence of the iterations to the optimal solution.The particle updating expression can be expressed as:

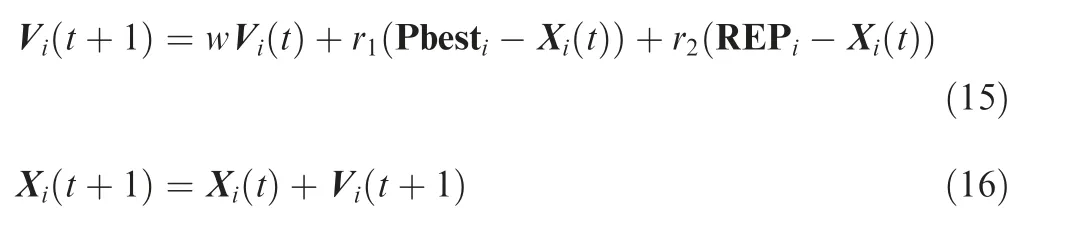
where X(t+1) is the position of one particle in its (t+1)th iteration. V(t+1) is the velocity of the particle during its(t+1)th iteration. The velocity V(t+1) is a weighted sum of the three factors:V(t),the best position in the particle population Pbestand the global best vector from the repository REP. w is the inertia weight. rand rare random numbers in the range [0,1]. Pbestis the best position that each particle in population and REPis a vector that is taken from the repository. With the velocity determined, the position of the particles can be easily determined with the Eq. (16).

With N updated particle positions, Pbestcan be obtained by the Pareto dominant comparison while the true challenge comes from REP. To obtain the global best vector, a repository is built to collect the non-dominated vectors from each iteration. Then a hypercube is established according to the objective function values of each non-dominated vectors.The hypercube is divided into grids and each grid was assigned a fitness.Then the REPcan be randomly selected from the fitness.The repository has a fixed volume.When the repository is full,it removes a solution from the repository according to the density. During the iteration, the necessary operation should be taken if the particles go out of a valid space. A detailed description can be found in literature.

Fig. 3 Flowchart of the MOPSO algorithm for LEO-NA constellations design problem.

For the MOP problem, it is difficult to define the iteration termination criteria according to objective function values.Hence it is often empirically determined. In this study, the number of maximum iteration is given as 200 to balance between the computation efficiency and computation burden.After the iteration procedure is finished, a set of Pareto optimal solution is obtained,and we need to pick out one solution as our final constellation design.

3.3. Selecting the best tradeoff constellation with fuzzy set method

The MOPSO algorithm provides a set of non-dominated solutions,while we need to pick out one particular constellation in practice.Although it is impossible to judge which Pareto optimal solution is better in the solution set, we have to pick out only one solution according to a certain rule. In this study, a fuzzy set algorithm is introduced to determine the final optimal solution.The fuzzy set algorithm computes a score for each solution in the solution set and picks up the solution with the highest score.The score is derived by normalizing the objective function values, given as:

4. Experiment setup

To evaluate the performance of the optimized constellations,we evaluated the performance of the MOPSO algorithm with numerical simulation. In this study, we assume the total satellite number is fixed as the external constraint. We considered two LEO constellations with 144 and 288 satellites respectively. The 288 satellites come from the Teledesic constellationand the 144-satellite constellation is designed with a half satellite number of the Teledesic constellation and there have been a few LEO constellation plans with around 150 satellite number, such as the Hongyan constellation.

With the total satellite number determined, we investigated the constellation configuration impact on the navigation performance with different optimization strategies. We designed three different constellation structures for each constellation,given as:

Scheme I.Polar constellation.The polar constellation is the most popular; hence we use the polar constellation as the reference. The orbit altitude and orbit plane parameter of the polar constellation comes from the single-layer constellation optimization results.

Scheme II. Single-layer 2D-LFC constellation. We optimized one set of constellation parameters with the MOPSO algorithm.

Scheme III. Two-layer 2D-LFC constellation. The total satellites are divided into two sub-constellations with different configurations,and these two sub-constellations are optimized together with the MOPSO algorithm.

Since the LEO -NA is working together with the existing GNSS constellations, hence we also involve multi-GNSS constellation in the constellation optimization. We consider the GPS, GLONASS, Galileo and Beidou-3 constellation in this study. The simulated constellation information of GNSS comes from their official interface control documents(ICD)and the details are presented in Table 3. It should be noted that the simulated constellation parameters are from the nominal configuration (see Table 4).Table 4.

During the constellations optimization procedure,the Simplified General Perturbations satellite orbit model 4 (SGP4) orbit propagator is used to compute the satellite coordinates from the constellation parameters. The optimization objectives are computed with the LEO and the four GNSS constellations and then optimizing the LEO constellation with the MOPSO algorithm to strive for a better solution. In the MOPSO algorithm procedure, 30 initial seed constellations are generated initially.The optimization objectives are computed from 30,000 randomly generated global stations. The maximum iteration number is limited to 200 to avoid the divergence issue. After the MOPSOprocedure,the fuzzy set algorithm is used to select the best tradeoff constellations from the MOPSO outputs.

Table 3 The nominal constellation configurations of four GNSS systems.

Table 4 The best trade-off solutions of 2D-LFC configurations.

5. Results and discussion

The simulation results are presented in this section, where reveals the benefit of the multi-objective optimization in the LEO-NA constellation design problem.

5.1. Optimized constellations in different schemes

Considering the two constellations with different satellite numbers,we designed three different constellation schemes for each constellation and the constellation configuration is presented in Fig. 4. The table indicates that the orbit inclination of the single-layer constellation is around 78° to balance the performance between the polar region and equatorial region. For the two-layer constellation, the orbit inclination is a combination of high inclination and low inclination sub-constellations.The optimal orbital altitude is generally higher than 1200 km.It should be noted that to ensure the fair comparison,the orbit altitude of the polar constellation is set the same as the optimized single-layer constellation.

The objective function value derived from the 6 optimized constellations is given in Table 5.The table indicates that general two-layer constellation achieves the smallest mean PDOP value, larger mean visible satellite number and lower mean orbit height, followed by the single-layer constellation.Although the polar constellation has the same orbital altitude and orbit plane number as the single-layer constellation, its performance is not as good as the optimized single-layer constellation.

To quantitatively evaluate the benefit of the MOPSO optimization, we adopt the membership score as the overall performance indicator. This membership score can be used to pick up the best trade-off solution from the Pareto solution set, and also can be used to evaluate the quality of the solution.

The membership score comparison results are illustrated in Fig. 5, and L-P, L-1 and L-2 represent polar constellations,single-layer constellations and two-layer constellations,respectively. The figure indicates that the optimized single-layer and two-layer constellation achieves better membership scores than the polar constellation, especially for the two-layer constellation, which improves the membership score by 75.7% and 42.7%. Although the orbit altitude and orbit plane number are the same for the polar and single layer constellation, the latter constellation still gain 7.46% and 5.17% performance improvement by optimally determine a more reasonable inclination and phase parameter. The 144 constellation achieves more significant performance improvement than the 288 constellations in general.

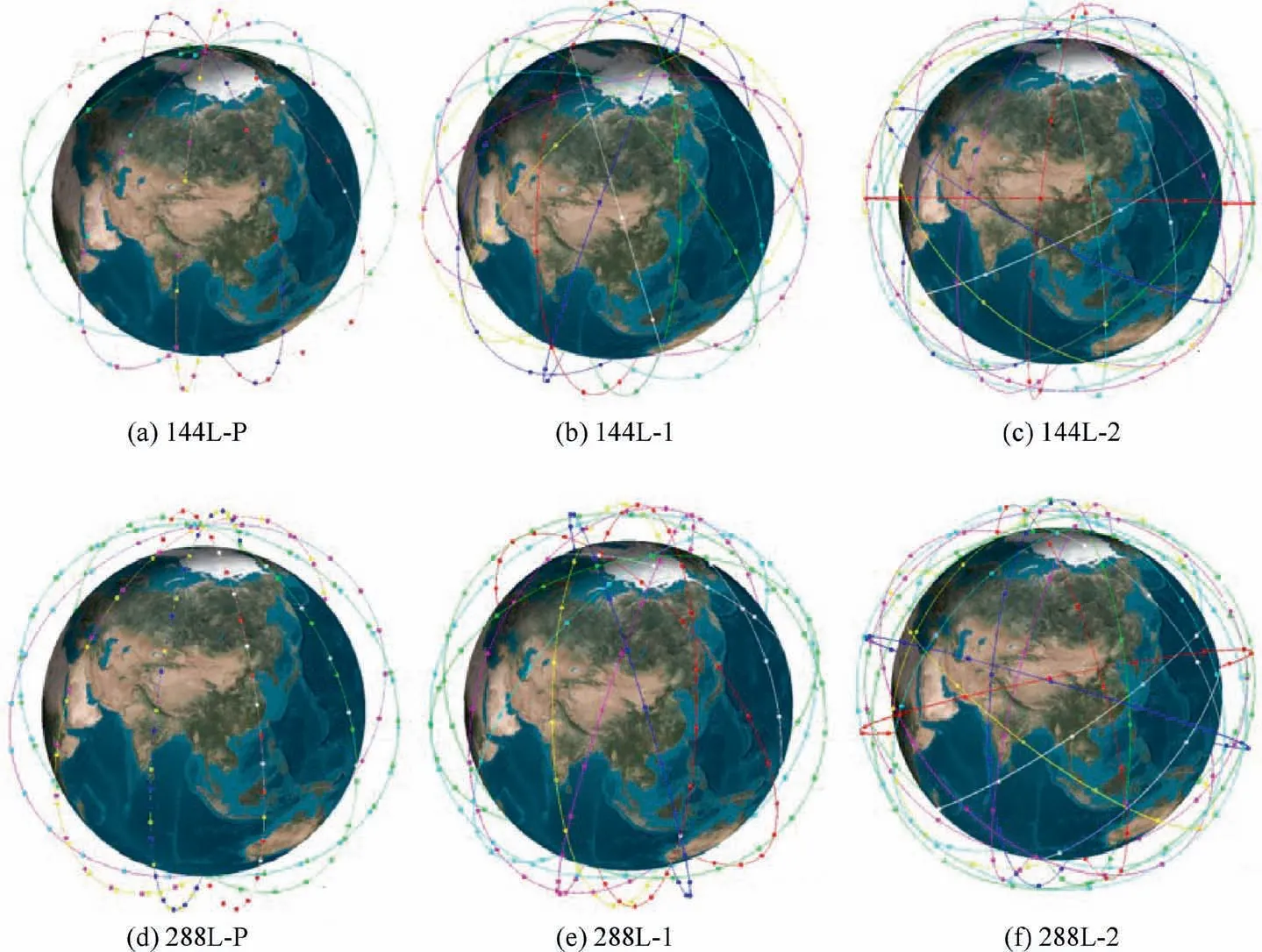
Fig. 4 Different configuration of the optimized constellations.

Table 5 The value of three objective functions with tradeoff 2D-LFCs.

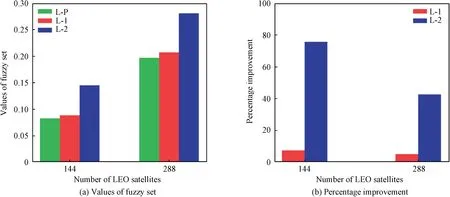
Fig. 5 The overall augmentation performance with three different designs.

5.2. Global analysis of LEO-NA constellation performance

The performance of the optimized constellations can be evaluated from two performance indicators: the PDOP and visible satellite number. To reasonably reflect the global variation of the PDOP and visible satellite number,we randomly simulated 30000 stations and a one-minute sampling interval is used to capture the spatial and temporal variation of the performance measures. The mean visible satellite number of different constellation schemes are presented in Fig.6.The figure compares the 144-constellation and 288-constellation respectively. The figure indicates that the polar constellations have the largest discrepancy between the polar region and the equatorial regions.Generally,the polar region has 4 times visible satellite more than the equatorial region, which is not reasonable. It means the system performs best in the polar region where only pretty few human activities occur. The optimized single-layer constellation obtains a more even distribution of the visible satellite than the polar constellations,but the polar region still has about 2-3 times visible satellites than the equatorial regions. The optimized single-layer constellation achieves performance improvement, but it still does not meet the expectations.The major reason is the polar constellation is not flexible enough, and it cannot balance the polar region and the equatorial region simultaneously. In contrast, the optimized two-layer constellation achieves more homogeneous coverage for both 144- and 288-satellite constellations. Although the polar region also has a more visible satellite as well, the equatorial region also dramatically increased its visible satellite number. The reason for the improvement is the second subconstellations can make up the weakness of the polar and single-layer constellation in the equatorial region. Hence the two-layer constellation achieves more homogeneous global coverage and more suitable for the LEO-NA applications.

We further compared the Cumulative Distribution Function (CDF) of the visible satellite number subject to different constellation designs and the results are presented in Fig. 7 The CDF can reflect the distribution of the visible satellite number on a global scale. The figure indicates that the twolayer constellation has a sharper CDF curve, which means the visible satellite number is more homogeneous.It also indicates the optimized two-layer constellation achieves at least 6 visible satellite number for over 99%time and locations,while the polar and single-layer constellations only ensure 3-4 visible satellite number with the 144-satellite constellation. For the 288-satellite constellation, the two-layer constellation has 10 minimum visible satellites while the minimum visible satellite number for the polar constellation and single layer constellation is about 7. Besides, the polar constellation and singlelayer constellation has a longer tail,which means some regions may be able to track more than 20 visible satellite number.According to Fig.6,we conclude the polar region has the most visible satellite number in the polar region. The optimized single-layer constellation performs did not outperform the polar constellation too much since the polar constellation uses the orbit altitude and plane number from the single-layer optimization results.According to Fig.2,a more visible LEO satellite number can help to reduce the precise positioning convergence time. The constellation with large visible satellite number discrepancy may not lead to a homogeneous global service standard. Particularly, the equatorial region obtained the poorest performance is not acceptable for the LEO-NA system.

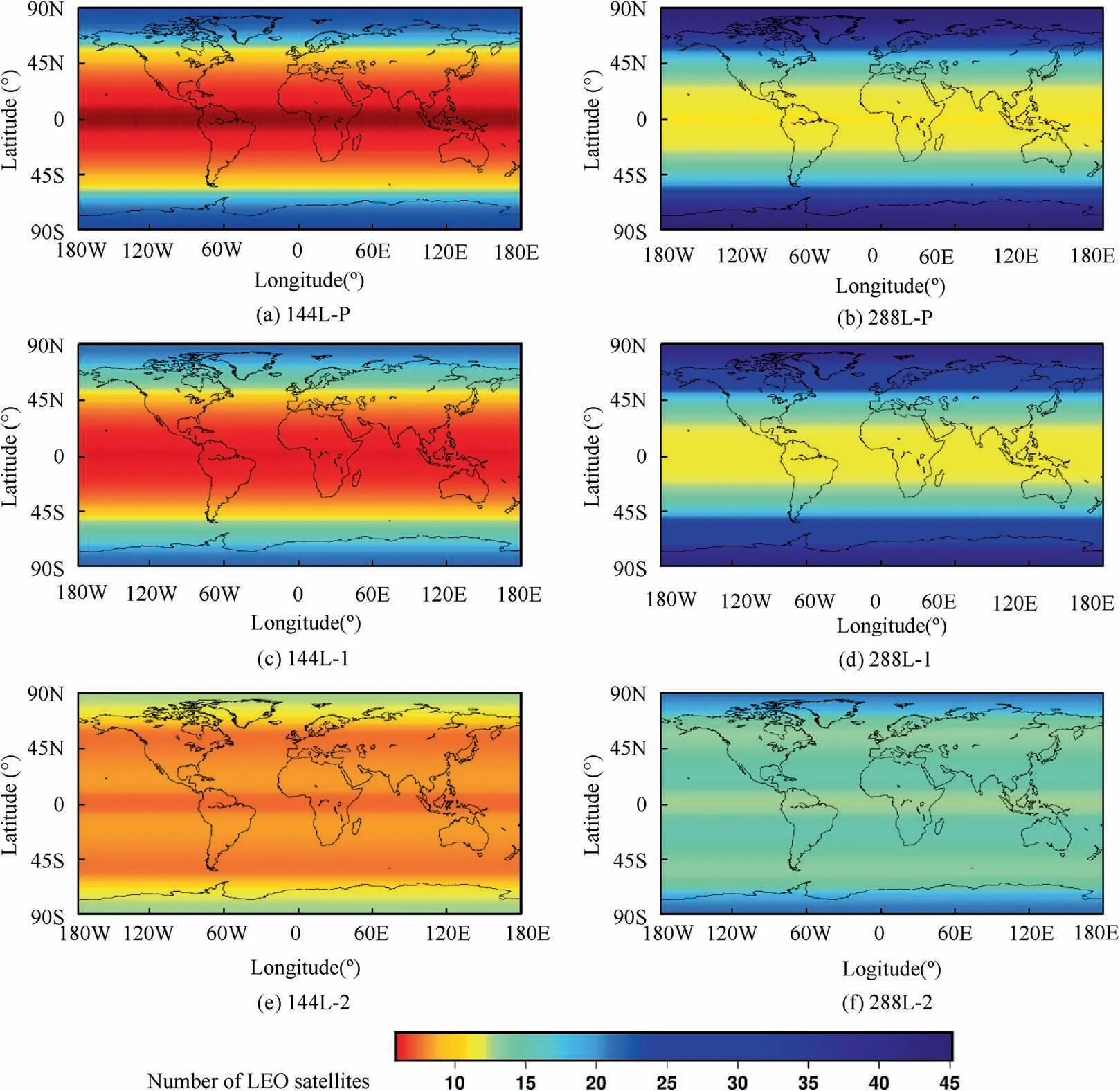
Fig. 6 Mean visible LEO satellites number for different LEO constellation systems.

Fig. 7 Comparison of visible LEO satellites’ cumulative probability for a 7 deg elevation mask.

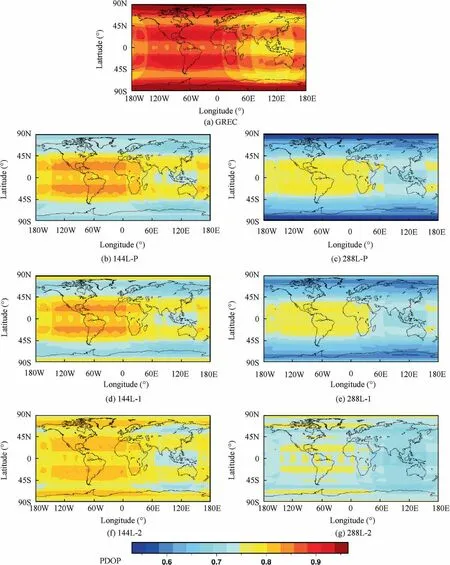
Fig. 8 The mean PDOP value distribution for different LEO constellation systems.

The second aspect of assessing the LEO-NA system performance is the PDOP values. Since the LEO constellation is an augmentation of the existing GNSS system, we have to consider the compatibility of the augmentation constellation and the existing constellations. In the PDOP value evaluation, we considered the four existing GNSS constellations and combined them with our LEO-NA constellation to explore their joint effort on user positioning. The mean PDOP distribution for the two constellations with different configurations is presented in Fig. 8, while GREC means the PDOP with current quad-GNSS constellations. The figure indicates that the LEO constellation is contributed to the global PDOP values and provides better satellite geometry for GNSS positioning. The global PDOP value varies between 0.75 and 1 for the quad-GNSS constellation.While the global PDOP value can be further reduced to 0.5-0.85 with the LEO-NA constellation.Benefiting from the BeiDou GEO and IGSO satellite, the Asia-Pacific region achieves the best PDOP value over the world.Generally, the PDOP value is affected by the LEO constellation design. The polar constellation achieves the best PDOP at the polar region,but a relatively large PDOP at mid-low latitude region. The two-layer constellation achieves a more homogeneous PDOP distribution over the global, generally,and the PDOP varies between 0.7 and 0.8 for most cases.

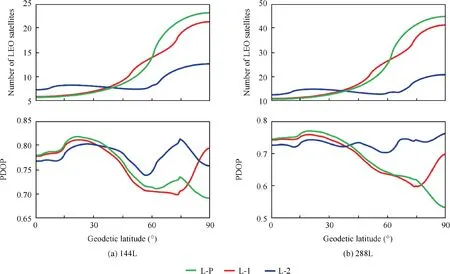
Fig. 9 Number of LEO visible satellites and average PDOP values for 144-LEO constellation systems.

The latitude is the dominating factor of the PDOP distribution, and so we quantitatively analyzed the relationship between the latitude and the PDOP distribution and the results are presented in Fig. 9. The figure presented both the visible LEO satellite number and the PDOP, which indicates that a more visible LEO satellite does not mean smaller PDOP value.Generally, all three constellation schemes have a more visible LEO satellite at the polar region, but the two-layer constellation outperforms the other two schemes in the latitude region of lower than the 40-degree region,where has the most intense human behaviors. The single-layer constellation outperforms the polar constellation in the middle latitude region. The two-layer constellations achieve the most homogeneous constellation out of the three constellation designs.

5.3. Temporal analysis of LEO-NA constellations performance

The continuity is also critical for the navigation service, so we need to evaluate the performance of the LEO-NA constellation from the temporal perspective. Satellite navigation requires continuous and stable service capacity. To explore the LEONA constellation impact on the temporal dimension, we selected three stations from the Multi-GNSS EXperiment(MGEX) network with different latitudes. The locations of these stations are shown in Fig. 10 and these three stations are located in the low, middle and high latitude regions respectively.

Fig.10 Location of the selected three GNSS monitoring stations from the MGEX network.

The time series of the visible satellite number and PDOP value of the three stations are presented in Fig.11.The visible satellite number and PDOP value are fluctuated fast, due to the fast movement of the LEO satellites. Considering the visible satellite number,the two-layer constellation has superiority on GLPS and GMSD station while it has less visible satellite than the two constellation schemes for the NYA2 station,which is located in the polar region. The two-layer constellation can provide 6 visible LEO satellite at a minimum while the other constellations only have 5 visible satellite occasionally. Considering the PDOP value, the figure indicates that the LEO constellations contribute to reducing the PDOP value.The two-layer constellation presents superiority in terms of PDOP for the GLPS station at the low latitude and comparable PDOP value in the middle latitude. Although the polar constellation has 8-10 more visible satellites than the twolayer constellation, it does not present dramatic PDOP improvement in the polar region.The PDOP value of the polar constellation presents fierce fluctuation in the polar region,although sometimes it performs the best.

The mean PDOP value of these three stations is presented in Table 6.The table indicates that the two-layer constellation has smaller mean PDOPs for the GLPS and GMSD stations,but the polar constellation achieves the best mean PDOP value for the NYA2 station.

Fig. 11 Comparison of visible LEO satellite temporal variation for 144-LEO satellite constellations in three latitudinal stations for a 7 deg elevation mask.

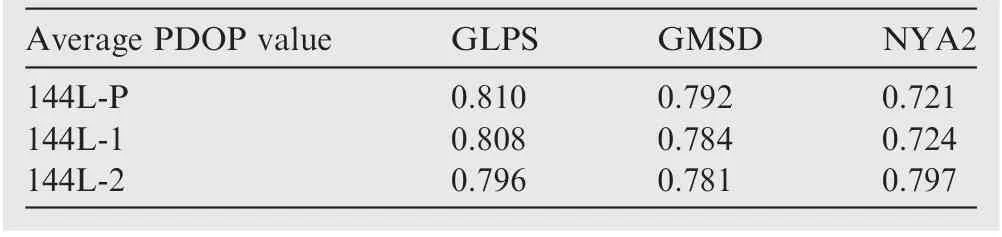
Table 6 Mean PDOP values with 144-satellite configurations in different stations.

6. Conclusions

The LEO navigation augmentation technique is considered as a promising application to extend and augment the existing GNSS system. Several pioneer research has been investigated the potential benefit of the LEO-NA system,but the constellation design problem has not attracted enough attention.In this study, we modeled the LEO-NA constellation design problem as a MOP and derived three performance measures of the LEO-NA constellations, namely orbit altitude, visible satellite number, and PDOP value. The MOPSO algorithm is used to solve the LEO-NA constellation design problem.Then the best trade-off constellation design is selected from a set of Pareto optimal solution with the fuzzy set method. The performance of the MOPSO based LEO-NA constellation design is validated with a 144-and 288-satellite constellations.We designed three schemes for each constellation, the polar constellation,single-layer 2D-LFC constellation, and two-layer 2D-LFC constellations. The results indicate that the single-layer and two-layer constellation optimized by the MOPSO achieves 5%-8% and 40%-75% overall performance improvement comparing to the polar constellation for the 144- and 288-satellite constellation respectively. The optimized two-layer constellation has a significant benefit in the mid-low latitude region coverage and thus produced the more homogeneous global coverage.The polar-constellation achieves the best performance in the polar region,but less coverage in the mid-low latitude. The single-layer constellation is also slightly better than the polar constellation in mid-low latitude by optimally design the orbit inclination and phase parameter. It concludes that the MOPSO algorithm can provide a more reasonable LEO-NA constellation design and the two-layer constellation is recommended for the LEO-NA constellation due to its homogeneously global coverage.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

s

The numerical calculations of this paper were done on the supercomputing system in the Supercomputing Center of Wuhan University. This study was co-supported by the National Natural Science Foundation of China (Nos.41704002, 91638203, 41904038).