Filters for manufacturability in design optimization of variable stiffness composites

Ye TIAN, Yuhng HUO, Tielin SHI, Qi XIA,b,*

a State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, China

b State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China

KEYWORDS Composite laminates;Design optimization;Fiber angle;Filter;Manufacturing constraints

Abstract In the design optimization of variable stiffness composites, manufacturing constraints imposed by the automated fiber placement technology must be considered. In the present paper,two filters are proposed to address this issue, and they are incorporated into the Shepard interpolation-based design optimization framework developed in our previous studies. The fiber angle arrangement of a composite is represented by a continuous function that interpolates fiber angles at scattered design points. Two filters are appointed for each design point to deal with two typical manufacturing constraints, i.e., fiber curvature and gap/overlap. At each design point,the sensitivity is first filtered in a rectangular region around this point, and by this means the fiber curvature is controlled;then in another rectangular region around this design point,the filtered sensitivities are averaged, and the result is used to update the corresponding design variable. Several numerical examples are investigated, and the results show that the proposed method is effective.©2020 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. Introduction

Fiber-reinforced composites, for instance constant or variable stiffness composites,are widely used for aeronautics and astronautics engineering.In the constant stiffness composites,the orientation of fibers is fixed in each ply, but in the variable stiffness composites (VSC) the fibers can be curvilinear.The latter has larger design freedom than the former, but its manufacturability becomes an important issue and poses a lot of difficulties.More specifically,the automated fiber placement (AFP) has two key constraints.First, the curvature of fiber paths should be smaller than the maximum allowable curvature. Otherwise, wrinkling and delamination may appear.Second, gaps or overlaps are not allowed. Therefore, adjacent fiber paths are required to be parallel.

In order to seek the optimal fiber layout of VSC,early studies directly optimized the fiber angles at finite element centers.Such optimization may result in the discontinuous fiber layout. To improve the smoothness of fiber orientation,various approaches have been proposed. For instance, Parnas et al.used cubic Bezier curves to describe spatially varying fiber angles. Kiyono et al.proposed the normal distribution fiber optimization method and used a spatial filter to achieve fiber continuity. However, these impressive studies ignored the constraints coming with the AFP manufacturing.

Recently,the issue of manufacturing constraints has caught much attention in the studies for the design optimization of VSC. Brampton et al.employed level set function to represent equally spaced fiber paths. Brooks and Martinstreated fiber paths as the field streamlines and considered gap-overlap and curvature constraints by controlling the curl and divergence of the vector field respectively. Zhou et al.enforced the restriction on the curvature of the fiber orientation by setting a filter radius. Demir et al.utilized a penalty parameter to control elemental curvatures.Hao et al.proposed a multistage design strategy based on lamination parameters,in which the curvature and parallelism constraints were formulated as inequalities by using path functions.These studies can improve the manufacturability of variable stiffness design. Nevertheless, on the one hand, some workmerely considered one of the manufacturing constraints.On the other hand,some researchintroduced a lot of constraints in the optimization problem, which may lead to low computational efficiency.

In the present work, an alternative method is proposed for the design optimization of manufacturable variable stiffness composites. The method is based on a framework developed in our previous studiesfor optimizing the fiber angle arrangement with spatial continuity. To be more specific, the fiber angles at finite element centers are computed by using a continuous function.This function is constructed by the Shepard method that interpolates the fiber angles at scattered design points. A gradient-based algorithm is then used to update the design variables. The algorithm can find the optimal solutions faster than heuristic algorithms. In the present study, two filters are appointed for each design point to deal with two typical manufacturing constraints, i.e., fiber curvature and gap/overlap. At each design point, the sensitivity is first filtered in a rectangular region around this point, and by this means the fiber curvature is controlled; then in another rectangular region around this design point, the filtered sensitivities are averaged,and the result is used to update the corresponding design variable. It can be seen that these filters prevent the optimization problem from a huge number of constraints.

2. Parameterization scheme of fiber angles based on Shepard interpolation

In the design optimization of VSC with curvilinear fibers, a fundamental issue is how to parameterize the fiber angle arrangement. In our previous studies, inspired by the work of Kang and Wang, we employed the Shepard interpolation for the representation of the fiber angles throughout the design domain.It ensures the fiber continuity of the composite. The parameterization scheme of fiber angles is given by

where ‖x-p‖ is the Euclidian distance between the point x and the design point p; p is a positive power parameter. For the composite structure with a hole or crack,the Euclidian distance is replaced by the geodesic distance.Besides,p is set to 2 in the method,since this makes the weighting function w(x )continuous and infinitely differentiable.As a result,the spatial continuity of the fiber angle arrangement is inherently guaranteed. Moreover, another property of Shepard interpolation is given as

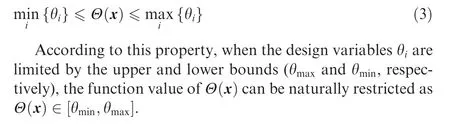
3. Finite element analysis of fiber-reinforced composite structures

In the present study, the plane-stress problem is considered.The structure is discretized by using the quadrilateral elements.There is an assumption that the fiber angle within each element is constant. For each finite element, the elemental stiffness matrix is given by

where Dis the original elastic matrix without fiber rotation;T(θ) is the rotation matrix given by

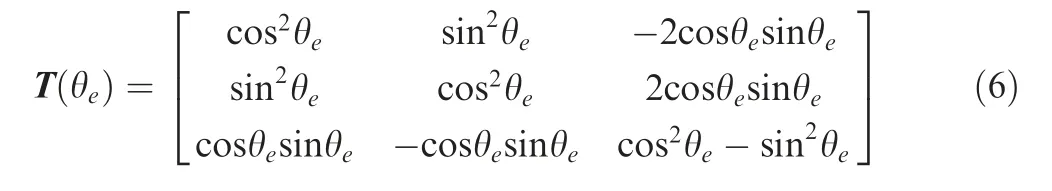
4. Optimization problem, sensitivity analysis and filtering

The compliance minimization problem for variable stiffness structures is considered in this paper. The formulation of the optimization problem is written as

where the fiber angles θat the design points pare taken as design variables; the objective is to minimize the compliance c,i.e.to maximize the stiffness of structure;Ku=f is the equilibrium equation in finite element analysis, in which f is the external force; the design variables are constrained between the lower bound θand upper bound θ, aiming to avoid the‘‘π-ambiguity” issue of fiber angles.

The redesign rule defined in the previous paper is higheffective to update the design variables.In the present study, the gradient-based redesign rule is also applied. The derivative of the objective function c with respect to the design variable θis given by

where xis the coordinate of the e-th element center.

In the SIMP (Solid Isotropic Material with Penalization)method for structural topology optimization, sensitivity filters or density filters are effective to deal with numerical instabilities including checkerboards and mesh-dependencies,and different types of filters were developed.Recently,several papers show that the filtering techniques have been applied in the combined topology and material orientation optimization.The purpose is to improve the fiber continuity and control the fiber curvatures. However, there is no reported usage of filters to simultaneously meet the curvature and gap-overlap constraints in VSC.

In our present study,the derivative ∂c/∂θobtained by Eq.(8) is successively filtered in two different rectangular regions.The first rectangular region R, as shown in Fig. 1(a), is centered at the design point i.Its longer side is along the fiber orientation θat the design point.The length of the long side and the short side are denoted as aand brespectively.To control the fiber curvature, the derivative ∂c/∂θis filtered as

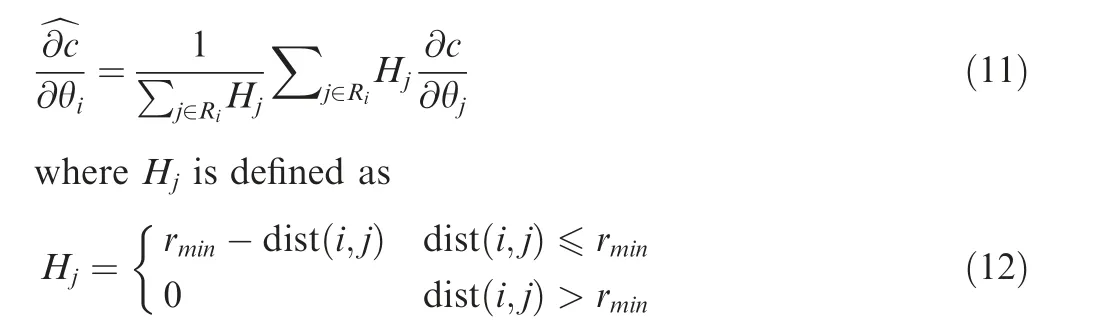
where ris a radius parameter; dist(i，j ) is the Euclidean distance between the design point i and any other design point j within the region R.

The second rectangular region Tfor design point i is shown in Fig.1(b).Its center is also located at the design point i.The long side of Tis perpendicular to the fiber orientation θ. In practice,the length of the long side(denoted as a)is generally five or more times that of the short side (denoted as b). To ensure parallel fiber paths, the average of the modified derivatives within Tis calculated as

where N is the number of design points in the region T.Instead of the original sensitivities Eq.(8), the filtered sensitivities Eq.(13) are used in the redesign rule to update the design variables.More importantly,the two filters can be applied several times.

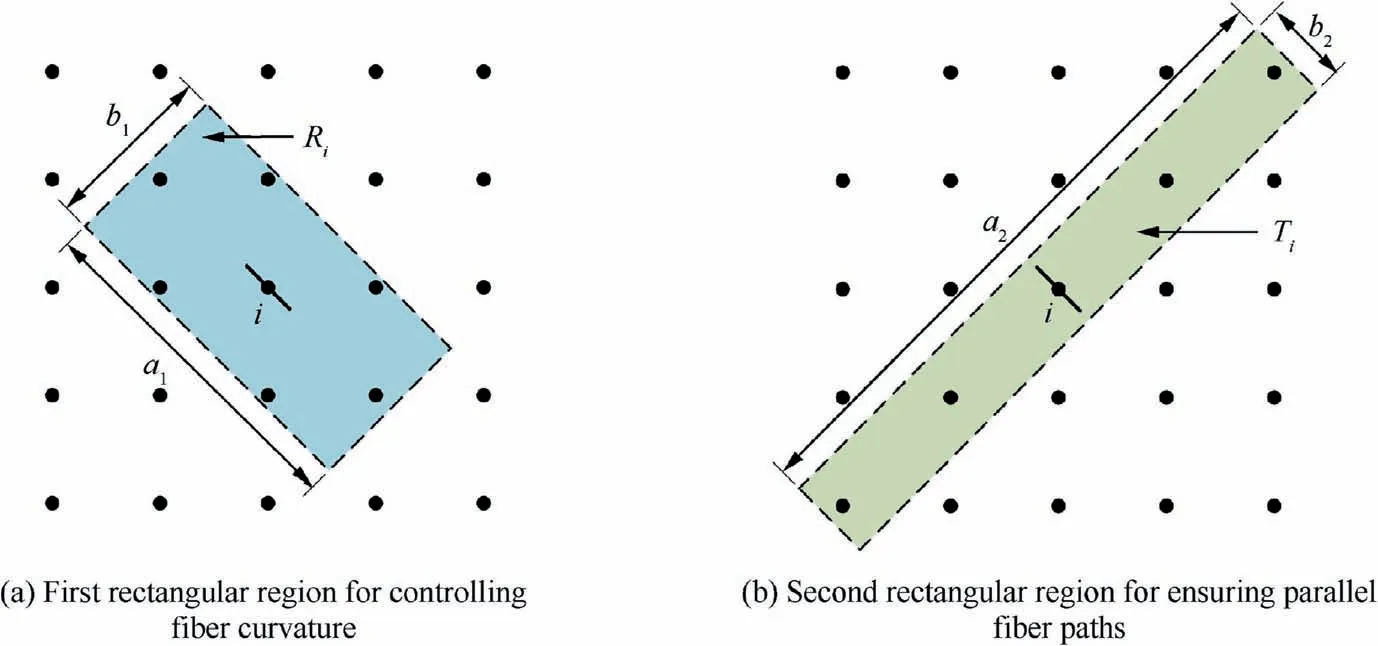
Fig. 1 Schematic illustrations of two filter regions (black dots represent the design points).

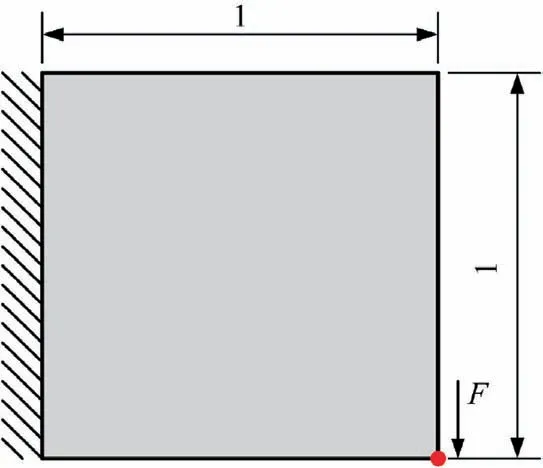
Fig. 2 Optimization problem of the first example.

5. Numerical examples and discussions

For all numerical examples in the paper, the property parameters of the composite material are assumed that E=1,E=0.05,G=0.03,v=0.3 and v=0.015.The thickness of the composite plate is set as 1,and the self-weight is not considered. The scatted design points are uniformly distributed with a spacing denoted as h. Furthermore, the dimensions of the two rectangular filtering regions are set as a=5h,b=2h, a=10h, and b=h. To make the weights within these rectangular regions positive, the radius parameter ris equal to a.The convergence criterion is simple,i.e.,the optimization is terminated after 50 iterations.

With the purpose to obtain fiber paths from fiber angle distribution, we use the Tecplot software for visualization and post-processing.In fluid dynamics, it is well known that the velocity of any point in a flow field is tangent to the streamline through the point. For the element e in the design domain, a vector at the element center is defined by This vector is tangent to the fiber path through the element center. After importing the vector field constructed by Eq.(14), the Tecplot generates fiber paths.

5.1. Example 1

The optimization problem of the first example is shown in Fig.2.A square composite structure of size 1×1 is taken into account.The left side of the design domain is fixed.At the bottom of the right side, an in-plane load F=1 is exerted vertically. The square domain is discretized into 20×20 of square elements of size 0.05. Also, 10×10 design points are uniformly distributed in the design domain, thus the value of his equal to 0.1.The initial fiber angles at these scatted points are set to 90.

The results are presented in Table 1, including the optimized angles at the design points, the optimized fiber angles at element centers,and the fiber paths.The convergence histories are shown in Fig. 3, indicating that the compliances ofcomposites are effectively reduced. From Table 1, it can be seen that sensitivity filters in Shepard interpolation-based optimization method are effective to improve the manufacturability of variable stiffness design. When the number of filtering increases, the fiber curvature and parallelism becomes better,although the structural compliance becomes larger. In addition, the difference between the results obtained with fourtimes filtering and six-times filtering appears to be very small.This means that too many times of filtering is not necessary.As one looks carefully, the lower left part of the result obtained with six-times filtering shows that parallel fiber paths are more equidistantly spaced. Hence such results indicate that the sixtime filtering is an appropriate choice.

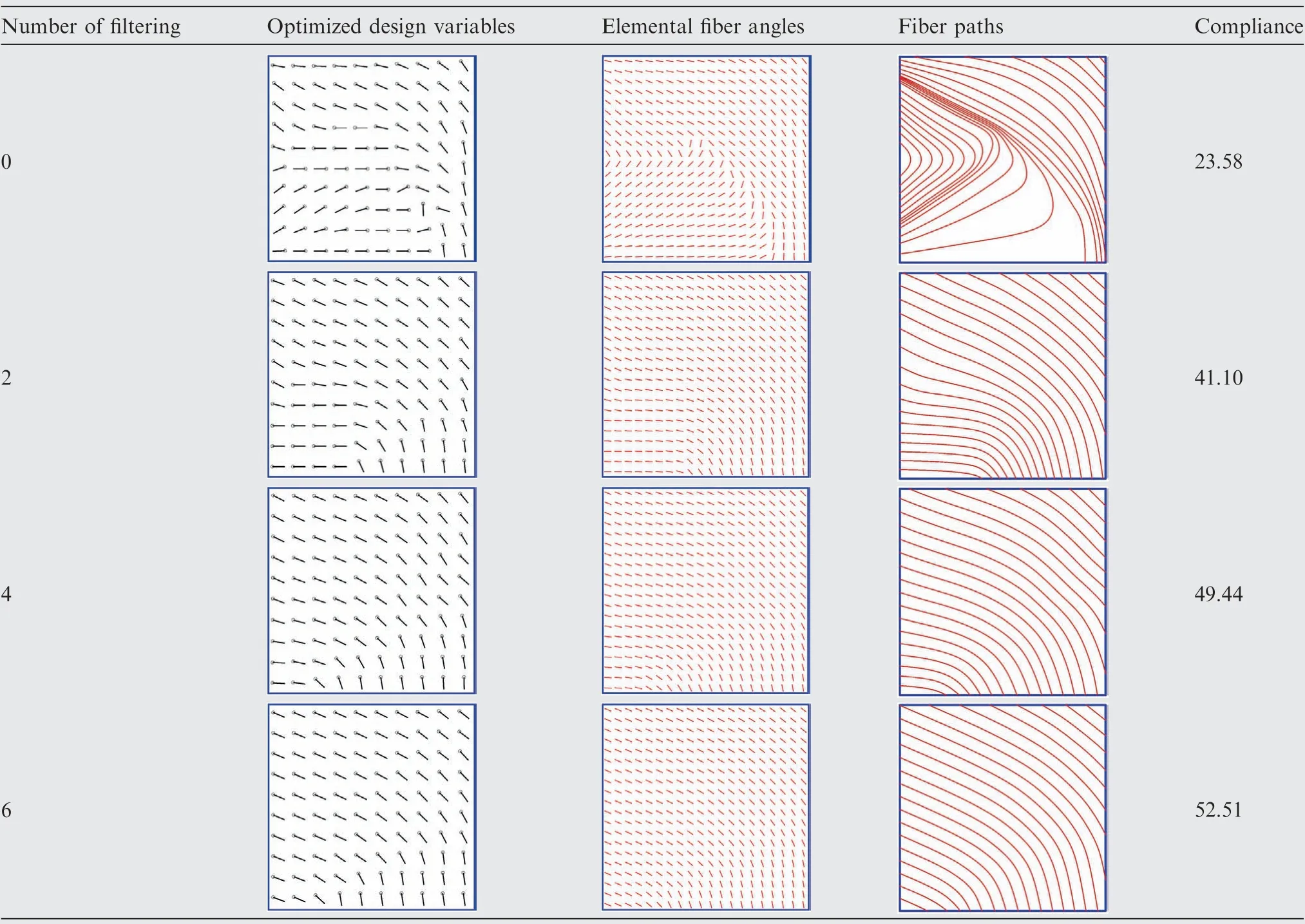
Table 1 Optimization results of the first examples.

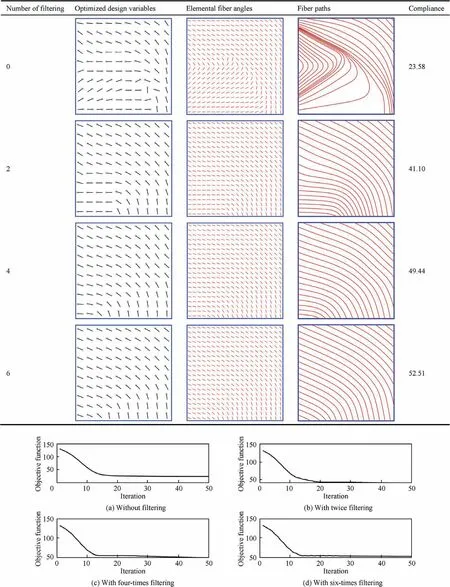
Fig. 3 Convergence histories of first optimization problem by using different filtering times.

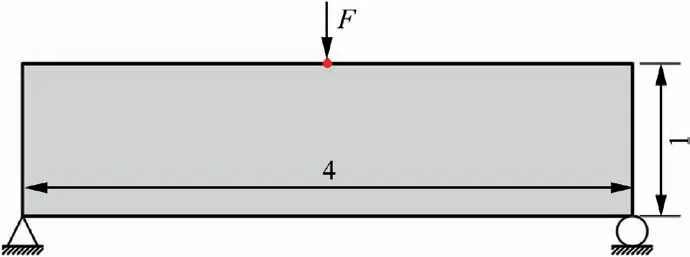
Fig. 4 Optimization problem of second example.

5.2. Example 2

The optimization problem of the second example is shown in Fig. 4. The design domain is a rectangle of size 4×1. The left side is fixed, and an in-plane concentrated load F=1 is applied vertically at the middle point of the upper side.Because of the symmetry, only the right half of the domain is analyzed. 40×20 square elements are used. Also, there are 20×10 design points evenly placed. The initial fiber angles at these scatted points are set to 0. According to the discussions in the first example, six-times filtering is done in the optimization.

Fig. 5 Optimized fiber angles at design points.

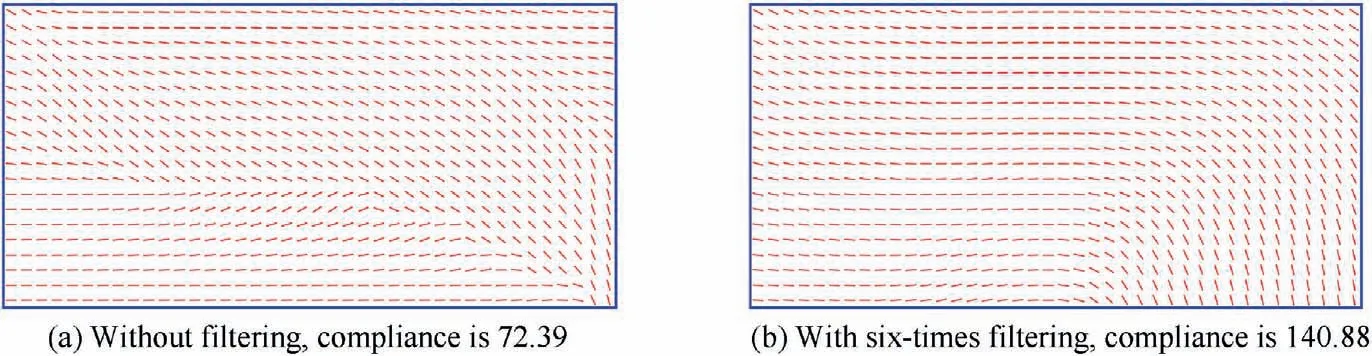
Fig. 6 Optimized fiber angles at element centers.

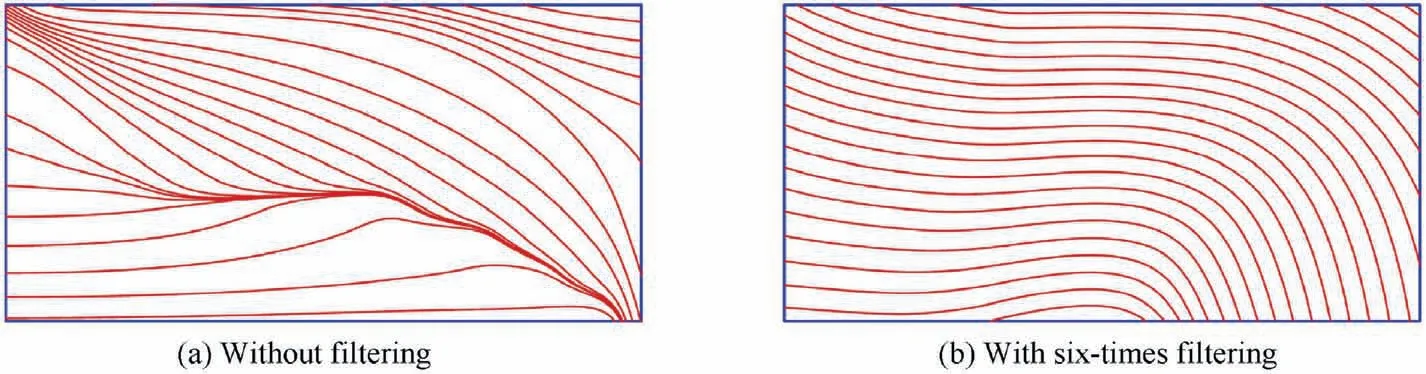
Fig. 7 Fiber paths plotted from optimal fiber angle arrangement of the structure.

Fig. 8 Convergence histories of second optimization problem.

The results of the second problem are shown in Figs. 5-7.As can be seen in Fig. 5, the optimized angle arrangement at the design points by using filters has a big change as compared to that without filtering. This leads to the better fiber orientation distribution in Fig.6(b).Then the fiber paths are obtained by the Tecplot software, as shown in Fig. 7. The comparison between Fig. 7(a) and (b) proves that sensitivity filters can effectively improve the manufacturability of the optimized variable stiffness structure. The convergence histories are shown in Fig. 8.

6. Conclusions

Conclusions are summarized in the following two points.First,filters in the Shepard interpolation-based method are used to deal with the manufacturability constraints of variable stiffness composite structures. The results of numerical examples show that the proposed method is effective to control the curvature and gap-overlap of fiber paths of the optimized design. Second, the influence of the filtering number on the optimization results is investigated. More times of filtering is beneficial for seeking the manufacturable design, but too many times appears to be unnecessary. In future work, the proposed method will also be applied to streamline stiffener optimization.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

s

This research work was supported by the National Natural Science Foundation of China(No.51975227) and the Natural Science Foundation for Distinguished Young Scholars of Hubei Province (No. 2017CFA044).