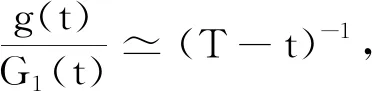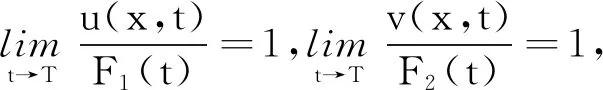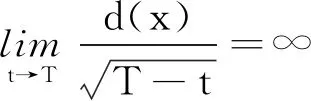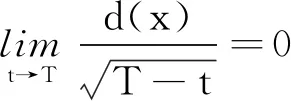非局部抛物方程组解的一致爆破及边界层估计*
林志强
(福州理工学院,福建 福州 350506)
1 主要结果
考虑如下具有非局部化反应源项的抛物型方程组初边值问题的正解:
(1)
其中:Ω⊂RN(N≥1)为有界区域,边界∂Ω充分光滑;参数α1≥0,β1≥0,α2>0,β2>0;初值(u0(x),v0(x))是非负非平凡函数,u0(x),v0(x)∈C2+α(Ω)(α∈(0,1)),且满足相容性条件.
有学者[1-5]研究了局部或者非局部的抛物方程组初边值问题解的爆破性质.笔者主要研究爆破解的一致爆破和边界层估计,在文献[1]的基础上得到以下结论:
定理1若以下任一条件成立:α1>1;β2>1;0<α1≤1,0<β2≤1,β1α2>(α1-1)(β2-1).则对于大初值,解(u(x,t),v(x,t))在有限时刻爆破.
证明参见文献[1]中的定理2.
定理2设(u(x,t),v(x,t))是方程组初边值问题(1)的解,若u(x,t)和v(x,t)在有限时刻同时爆破,则参数满足α2≥α1-1,β1≥β2-1,或者α2<α1-1,β1<β2-1.
定理3设(u(x,t),v(x,t))是方程组初边值问题(1)的解,且在有限时刻爆破,若α2≥α1-1,β1≥β2-1,则u(x,t)和v(x,t)同时爆破.
定理4假设定理2的条件成立,则在Ω的任意紧子集上一致成立:
(ⅰ)当α2>α1-1,β1>β2-1,β1α2>(α1-1)(β2-1), 或者α2<α1-1,β1<β2-1时,
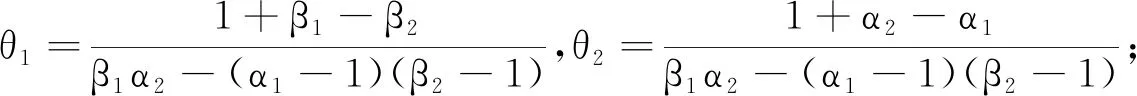
(ⅱ)当α2=α1-1,β1>β2-1时,
(ⅲ)当α2>α1-1,β1=β2-1时,
(ⅳ)当α2=α1-1,β1=β2-1时,
定理5假设定理4(ⅰ)的条件成立,则对于所有的C,存在t0∈(0,T),k2≥k1>0,使得

定理6假设定理4(ⅰ)的条件成立,且θ1>1,θ2>1,则存在k3>0,t0∈(0,T),对于∀(x,t)∈Ω×[t0,T),有
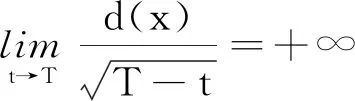
2 一致爆破模式
为了方便,记
定义1设f1(t)和f2(t)是定义在[0,T)的函数,若存在0 引理1[5]假设定理2的条件成立,则 0≤u(x,t)≤k2+F1(t),0≤v(x,t)≤k2+F2(t); (ⅲ)在Ω的任意紧子集上一致成立 如果仅假定u在有限时刻T爆破,那么这些结论对u和F1成立;同理,如果仅假定v在有限时刻T爆破,那么这些结论对v和F2成立. 定理2的证明由引理1(ⅲ)可知u(x,t)~F1(t),v(x,t)~F2(t),因此 (2) 由(2)式可知 (3) 当α2≥α1-1时,假定β1<β2-1.对(3)式两边积分,分2种情况来讨论:当α2=α1-1时,有 当α2>α1-1时,有 类似地,可以证明α2<α1-1,β1<β2-1. 证毕. 定理3的证明假定u在有限时刻爆破,v在Ω×(0,T)非负有界,由引理1(ⅲ)可知u(x,t)~F1(t),因此 因为v(x,t)非负有界,所以在Ω×(0,T)上,v(x,t)≥k>0,其中k>0.于是存在常数0 (4) (5) 由(5)式可得 证毕. 为了证明定理4,先引入如下结果: 引理2假设定理2的条件成立,则有: (ⅰ)当α2>α1-1,β1>β2-1,或者α2<α1-1,β1<β2-1时, (ⅳ)当α2=α1-1,β1=β2-1时,lnF1(t)~lnF2(t). 证明因为 所以 (6) (ⅰ)当α2>α1-1,β1>β2-1时,对(6)式两边从t0(>0)到t积分,可得 (ⅱ)当α2=α1-1,β1>β2-1时, (7) 对(7)式两边从t0(>0)到t积分,可得 (ⅲ)当α2>α1-1,β1=β2-1时, (8) 对(8)式两边从t0(>0)到t积分,可得 (ⅳ)当α2=α1-1,β1=β2-1时, (9) 对(9)式两边从t0(>0)到t积分,可得 于是lnF1(t)~lnF2(t). 证毕. 定理4的证明 (10) (11) (ⅰ)当α2>α1-1,β1>β2-1,或者α2<α1-1,β1<β2-1时.由(10)式和引理2(ⅰ),有 于是 即 (12) 由 (13) 从而,在Ω的任意紧子集一致成立 故 同理,在Ω的任意紧子集一致成立 (ⅱ)当α2=α1-1,β1>β2-1时.由引理2(ⅱ),有 于是 (14) (15) 根据L′Hospital法则,有 所以 (16) 由(15),(16)式可得 (17) 由u(x,t)~F1(t)在Ω的紧子集一致成立,令 即 从而 (ⅲ)当α2>α1-1,β1=β2-1时.证明与(ⅱ)类似,可得 (ⅳ)当α2=α1-1,β1=β2-1时.由(10),(11)式可得 (18) (19) 由(18),(19)式可得 于是 (20) 由引理2(ⅳ)可知lnF1(t)~lnF2(t),即 因此在Ω的任意紧子集一致成立 证毕. 作为讨论的基础,引用文献[5]中关于单个方程问题 (21) 引理3[5]假设g(t)≥0,w是问题(21)的解,且在有限时刻T爆破.若g(t)是标准的,则对于∀C>0,存在t0∈(0,T),k2≥k1>0,使得 引理4[5]假设g(t)≥0,在[0,T)上连续,在(0,T)上Hölder连续,w是问题(21)的解,在有限时刻T爆破,且w0(Ω)∈C0(Ω).若G1(t)是标准的,则存在k3>0,t0∈(0,T),使得 定理5的证明由定理4(ⅰ),有 已知f1(t),f2(t)在[0,T)上连续,在(0,T)上Hölder连续.由θ1>1,θ2>1,可得 (22) (23) 证毕. 定理6的证明 (24) (25) 对(24),(25)式积分,可得 经过计算可得 同理可得 因为-θ1<-1,-θ2<-1,所以F1(t),F2(t)是标准的.由引理4可得 (26) (27) 于是由(22),(23),(26),(27)式可得: 证毕.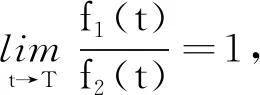
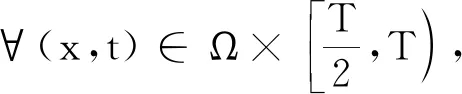
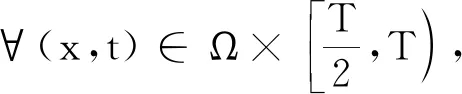

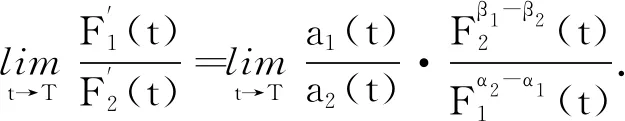
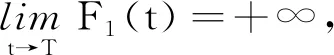
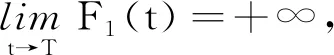
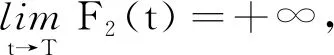
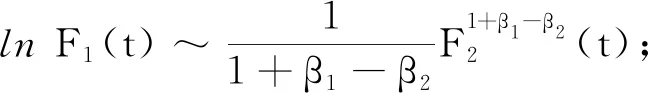



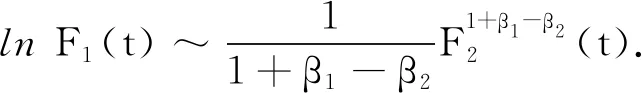

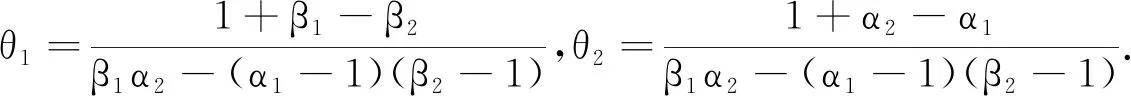
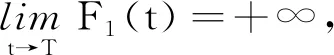
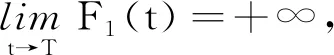





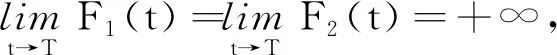
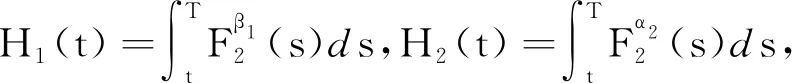

3 边界层估计