基于改进灰色神经网络的空中目标意图估计

于 果,王肖霞,吉琳娜,杨风暴

(中北大学信息与通信工程学院，山西 太原 030051)

0 引言

在现代防空作战中，对空中目标意图的可靠与准确估计不仅是战场态势评估的主要目的，更是战场指挥人员做出及时有效决策的重要依据[1]。对空中目标意图估计就是利用多传感器系统探测的战场信息估计目标的可能意图[2]。文献[3]运用层次分析法构建了以专家系统为特征的目标意图推理决策支持系统。文献[4]对战场事件分类定义，利用贝叶斯网络推理工具计算目标意图的概率。文献[5]利用Fisher与Bayes判别建立知识规则库，利用单时刻空中目标的属性值与规则匹配来估计意图。文献[6]利用不同意图下航向的变化趋势及专家知识构建模糊推理模型实现对空中目标的意图估计和识别。上述方法主要存在以下两种问题：第一，空中战场环境复杂多变，专家知识的不完备性等缺点会导致意图估计结果不可靠；第二， 仅考虑当前时刻的目标属性值而忽略历史状态对意图的影响，造成估计结果准确度较差。针对上述问题，本文提出基于IFOA-GNNM的空中目标意图估计模型。

1 灰色神经网络和果蝇优化算法

1.1 灰色神经网络(GNNM)

灰色神经网络是灰色系统与神经网络结合的一种新型智能计算模型[7]，灰色系统以原始序列为基础建立微分方程，模型简单，但对序列预测的能力较差，神经网络具有较强的数据处理能力和自我修正能力，由于两者在信息上存在相似性，模型上具有互补性，因此将两者结合产生的灰色神经网络能够弥补单纯使用一种模型的不足[8]，不但能够弥补神经网络需要大量数据训练的缺陷，还能够提高预测结果的准确性。

灰色神经网络的原理如下[9]：

假设有一组序列值：

x(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(1)

建立累加序列(AGO)：

(2)

为了方便理解，将原始序列x(0)记为x(t)，累加序列x(1)记为y(t)，预测结果记为z(t)，建立含有n个参数的灰色微分方程：

(3)

a和bi表示灰色神经网络的两个重要网络系数：发展系数和灰作用量。

解微分方程(3)可以得到：

令

(5)

将式(5)代入式(4)，可以得到：

(6)

灰色神经网络的结构如图1所示，将式(6)映射到结构中[10]，可以得到网络的输出为：

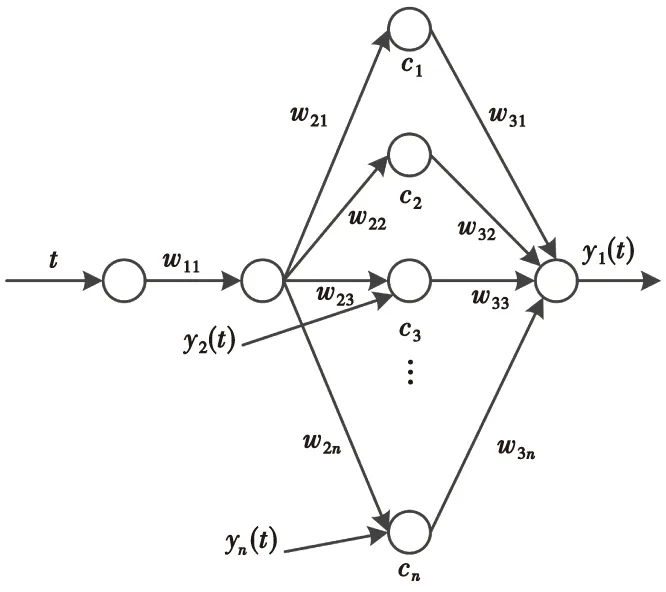
图1 灰色神经网络结构Fig.1 Network structure of GNNM

y1=w31c1+w32c2+…+w3ncn-θy1

(7)

(8)

式(8)中，w11表示输入层的权重，w2i表示输入层与隐藏层的权重，w3j表示隐藏层与输出层的权重，h表示输入层的输出，ci表示隐藏层的输出，θy1表示输出层的偏差值。

1.2 果蝇优化算法

1.2.1标准果蝇优化算法(FOA)

果蝇算法是由潘文超受果蝇觅食行为启发提出的一种新型种群智能优化算法[11]。依照果蝇搜寻食物的特性可以将该算法归纳为以下几个步骤[12]：

1)初始化果蝇群体位置X_axis、Y_axis。

2)设定果蝇个体i觅食的随机飞行方向和飞行距离。

Xi=X_axis+RandomValue

(9)

Yi=Y_axis+RandomValue

(10)

3)计算果蝇个体i距离原点的距离D和气味浓度判断值Si。

(11)

(12)

4)将气味浓度判定值Si代入气味浓度判定函数Function，求出该位置果蝇个体i的味道浓度Smell。

5)找出该果蝇群体中味道浓度(Smell)最大的果蝇，即为最优解。

Smell=Function(Si)

(13)

[bestSmell,bestIndex]=max(Smell)

(14)

6)保留最佳的气味浓度值与该浓度值下的果蝇坐标位置，使该果蝇群体利用视觉向该位置飞去。

Smellbest=bestSmell

(15)

X_axis=X(bestIndex)

(16)

Y_axis=Y(bestIndex)

(17)

7)通过迭代寻优，重复执行步骤2)—步骤5)，并判断每次迭代寻优的结果是否优于前一次迭代的结果，若是则执行步骤6)，直到迭代结束。

1.2.2改进的果蝇优化算法(IFOA)

标准果蝇算法在迭代寻优时步长是固定不变的，这意味着果蝇的每次随机飞行都被限制在一定范围内。步长过大会导致果蝇错过最优解；步长过小，果蝇收敛速度缓慢，极易陷入局部最优解。因此，为了保证算法能求得全局最优解，向标准果蝇算法中引入莱维飞行(Levy Flight)。

莱维飞行一般用于大范围的搜索中，比如苍蝇的飞行、动物寻找食物等等。莱维飞行通过大范围的搜索、折线的急剧转向帮助主体获得更多信息和视野。将其引入标准果蝇算法，能够有效避免由于步长不恰当引起的结果非最优性。

将莱维飞行引入标准果蝇算法能够保证算法求得全局最优解的原理如下：

步骤1)—步骤4)不变。

5)找出该果蝇群体中味道浓度(Smell)最大和最小的果蝇。

Smellbest=bestSmell

(18)

[bestSmell,bestIndex]=max(Smell)

(19)

[worstSmell,worstIndex]=min(Smell)

(20)

6)保留最佳气味浓度值及其最佳和最差气味浓度值的果蝇的位置。

Smellbest=bestSmell

(21)

Xb=X(bestIndex),Yb=Y(bestIndex)

(22)

Xw=X(worstIndex),Yw=Y(worstIndex)

(23)

7)计算种群的最大最小距离。

(24)

(25)

8)根据距离区分较优果蝇子群和较差果蝇子群，分别采取不同的飞行形式。

如果Db>Dw，较差子群在最优果蝇个体的指导下进行食物搜索；

Xi=Xb+RandomValue

(26)

Yi=Yb+RandomValue

(27)

如果Db

(28)

u=σ·RandomValue,v=RandomValue

(29)

(30)

step为莱维飞行的步长，较优子群作莱维飞行：

Xi=Xi+step·(Xi-Xb)

(31)

Yi=Yi+step·(Yi-Yb)

(32)

剩下的步骤与标准果蝇算法相同。

2 空中目标意图估计模型的构建

2.1 数据预处理

为了保证目标属性和意图类型的全面性，本文选取了空中目标的七个属性[13]：飞行高度、飞行速度、航向角、飞行加速度、距离、雷达反射面积、机动类型。

2.1.1一般目标属性的预处理

在对目标属性的预处理中，对于其值与威胁程度成正比的属性，如航向角、雷达反射面积，采用下列公式：

(33)

对于其值与威胁程度成反比的属性，如飞行高度、飞行速度、飞行加速度、距离，采用下列公式：

(34)

2.1.2特殊目标属性的预处理

目标的机动类型对于其意图的估计具有重要作用，在其他属性变化显著的情况下起辅助作用；在其他属性变化不明显的情况下，目标出现某种机动类型对于意图估计起决定性作用。本文中的机动类型及量化如表1所示。

表1 机动类型及量化Tab.1 Maneuver types and quantification

2.1.3单时刻多属性值的预处理

在对目标多维属性进行量化和标准化处理后，将单时刻的目标多维属性值融合成一个状态值。

设ti(i=1,2,…,10)时刻的空中目标的属性为：

(hi,vi,θi,ai,di,si,li)

(35)

式(35)中，hi表示目标的飞行高度，vi表示飞行速度，θi表示航向角，ai表示加速度，di表示距离，si表示雷达反射面积，li表示机动类型。

将序列(35)融合成状态值Pi，每个时刻的Pi值都能够体现该时刻目标的多属性信息，10个时刻形成一个状态序列：

(P1,P2,…,P10)

(36)

本文中向意图估计模型中输入的就是多组这样的状态序列对网络模型进行训练。

2.2 改进果蝇算法优化灰色神经网络

灰色神经网络有两个重要的系数发展系数和灰作用量，网络层之间的权重取值也是由这两个系数来定的，因此，它们对网络性能的发挥至关重要。采用改进的果蝇算法优化灰色神经网络也就是对这两个系数的最优求解。

用果蝇算法改进灰色神经网络的本质，就是将灰色神经网络的训练误差作为算法的适应度函数(目标函数)求得网络发展系数和灰作用量的最优解。

3 实验与分析

3.1 基准函数验证算法实验

为了验证改进后的果蝇算法的有效性，本文采取了八个基准函数[14]对标准果蝇算法和改进果蝇算法进行比较。这六个基准函数分别为：Sphere函数、Rosenbrock函数、Schwefel 2.26函数、Rastrigin函数、Ackley函数和Griewank函数，如表2所示。这些函数具有不同的性质，Sphere函数单调且仅有一个全局最小值，测试时不存在陷入局部最优解的问题，因此该函数主要是用来测试算法的收敛速度。Rosenbrock函数是一个非凸函数，也称为香蕉函数，它有多个极值，因此该函数用来测试算法的求解误差大小。Ackley函数常用来检测算法的全局收敛速度。Schwefel函数、Rastrigin函数、Griewank函数、Alpine函数及Step函数在迭代过程中都会产生大量局部极值，因此，这些函数用来测试算法全局最优解的求解能力。

表2 基准函数Tab.2 Benchmark functions

实验中，设置果蝇算法的种群规模为50，迭代次数为200，维度为10。实验结果如图2所示。

图2 不同标准函数下两种算法的收敛曲线比较Fig.2 Comparison of convergence curves of two algorithms under different benchmark functions

从实验结果可以看出，改进后的果蝇算法比标准果蝇算法具有更快的收敛速度，且求解的准确度有了很大的提高。从图2(a)、(b)可以看出，改进后的果蝇算法明显收敛速度更快，对于简单函数的求解比标准果蝇算法性能更好。从图2(c)—图2(f)可以看出，改进后的果蝇算法具备跳出局部最优解寻求全局最优解的能力。在图2(g)、(h)中，由于Alpine函数会产生大量可微的局部极值、Step函数会出现不同的阶跃现象，所以两者都具有较高的寻优难度。图2(g)中两种算法对于Alpine函数的寻优结果较好，且改进后的算法优于标准算法。但对于Step函数，从图2(h)中可以看到，两种算法的寻优结果都不理想，因此，说明果蝇算法对于Step函数的寻优是有缺陷的，这也是未来改进的一个方向，但即使在寻优结果不好的情况下，改进后的果蝇算法也显示出了较好的性能。

综上所述，该实验证明了改进后的果蝇算法具有更快的收敛速度、更准确的求解结果和更好的性能，向标准果蝇算法中引入莱维飞行来改进算法是科学有效的。

3.2 算法的时间与空间复杂性分析

为了评价改进后算法的工程价值及使用效率，需要考虑算法的时间和空间复杂性。时间复杂性指算法消耗的时间，一般采取大O符号表示法；空间复杂性指一个算法在运行过程中临时占用存储空间大小的一个量度。在评价算法的使用效率时一般以时间复杂性作为主要指标，因此，本实验主要是针对算法的时间复杂性。

为了使时间复杂性以直观的形式体现，本文在保证运行环境相同、数据规模相同、机器性能相同的条件下对原始灰色神经网络、标准果蝇算法优化后的灰色神经网络和改进后的果蝇算法优化的灰色神经网络三种方法的运行时间进行了统计。统计结果如表3所示。

表3 运行时间Tab.3 Running time

从实验结果看，GNNM运行时间最短，这是因为原始的灰色神经网络结构简单，网络参数随机选取，没有涉及求解最优值的复杂算法，因此，运行时间最短。FOA-GNNM运行时间为GNNM的3倍，这是因为在原始灰色神经网络的基础上加入了标准果蝇算法求取网络参数的最优解。IFOA-GNNM运行时间最长，因为改进后的果蝇算法计算复杂度增加了，以牺牲运行时间来保证网络的最优性能，运行时间的长短也是可以接受的。从算法的使用价值来看，一定时间的牺牲以确保算法的稳定性和最优性是值得的。

3.3 空中目标意图估计仿真实验

为了保证空中目标意图估计的可靠性，本文选取了10个单时刻属性值的变化来对意图进行估计。从数据仿真系统中可以获取大量单时刻的空中目标多属性值，这些属性分别为：飞行高度、飞行速度、航向角、飞行加速度、距离、雷达反射面积、机动类型。将这些属性融合成一个单时刻的状态值，将10个单时刻状态值作为一个时间序列输入意图估计模型，模型会根据输入的意图序列得出一个意图值，根据该意图值的大小判断属于哪个意图。本文中的意图类型有8个[15]：对地攻击、对空攻击、侦察、预警监测、电子干扰、诱敌、运输、撤退。

本文中意图估计模型的输入维度为10，输出维度为1，设置该实验中灰色神经网络的结构为1-1-10-1，网络学习次数为50。果蝇算法的维数为10，种群规模为50，迭代次数为200。该实验从仿真系统中选取120组数据，其中96组为训练数据，剩下24组作为测试数据。

为了验证该模型在对空中目标意图估计中具有较高的可靠性和准确性，本文分别将该方法与传统单时刻意图估计方法、灰色神经网络(GNNM)模型和标准果蝇算法优化的灰色神经网络(FOA-GNNM)模型进行了对比实验，实验结果如图3—图5、表4所示。

图3 单时刻与多时刻意图估计结果对比图Fig.3 Comparison of intention estimation results between single time and multi time

多时刻与单时刻意图估计结果如图3所示，从图中可以看出，用单时刻意图估计的方法估计出的意图值在真实值上下浮动较大，存在较大的误差，对战场指挥人员的参考作用不大。本文的算法虽然也存在一定误差，但意图估计结果的合理性与可靠性明显增强了。该实验证明多时刻意图估计结果的可靠性强于单时刻意图估计的结果，因此本文方法与传统方法相比对空中目标意图估计的结果更具优势。

图4分别是不同意图情况下3种模型对意图序列的估计结果比较。该实验一方面证明了灰色神经网络对时间序列估计的可行性，另一方面也显示了本文方法估计结果的准确性。在GNNM模型中，单独使用灰色神经网络，网络内部仅涉及简单的权重叠加公式，意图估计的结果误差较大，距离真实值最远；在FOA-GNNM模型中，向灰色神经网络中引入了标准果蝇算法，利用该算法对网络的初始参数求最优解，使该模型比GNNM模型具有更优的初始参数和初始权重，但标准果蝇算法由于步长取值随意，易陷入局部最优解，该模型意图估计的结果比GNNM模型准确了一些，但仍有进一步优化的空间；在IFOA-GNNM模型中，用改进后的果蝇算法对灰色神经网络进行优化，利用莱维飞行扩大果蝇的视野和搜索范围，保证算法求得全局最优解，也即求得灰色神经网络的最优初始参数，因此，该模型中对于空中目标意图估计的结果最接近真实值。

图4 不同情况下的空中目标意图意图估计Fig.4 Air target intention estimation under different situations

此外，本文还选取了相对误差(RE)和均方误差(MSE)两个指标对3种模型在对空中目标意图估计中的性能进行评估，其结果如图5和表4所示。从结果可以看出，IFOA-GNNM的相对误差和均方误差都是3种模型中最小的，因此，证明了改进果蝇算法优化的灰色神经网络模型在对空中目标意图估计中误差最小。

图5 相对误差比较图Fig.5 Comparison of relative error

表4 均方误差比较Tab.4 Comparison of MSE

4 结论

本文提出基于IFOA-GNNM的空中目标意图估计模型。该模型采用改进后的果蝇算法优化灰色神经网络挖掘空中目标多时刻属性的变化趋势与意图之间的隐含规则实现对空中目标的意图估计。仿真实验验证结果表明该模型在对空中目标意图估计中有着更强的可靠性和更高的准确性。如何使该模型适用于处理属性波动较大的空中目标，使结果稳定性增强是未来改进的方向。