基于改进CEEMDAN的微多普勒特征提取

金家伟，阮怀林，孙 兵

(国防科技大学电子对抗学院，安徽 合肥 230031)

0 引言

弹道目标在飞行时，为了保持飞行的稳定性，不仅会绕自身对称轴作自旋运动，还会由于受到横向作用力绕空间定向轴进行进动[1]。微动会对雷达回波产生频率调制，从而产生微多普勒效应[2-3]。微多普勒频率具有时变性，频谱分析法无法展现频率与时间的关系，因此，时频分析法被广泛应用于分析时变的微多普勒频率，因为时频分析法可以将一维信号映射到二维时频平面来同时显示信号的时频信息[4]。文献[5]提出一种基于参数化时频分析的进动锥裙目标微多普勒曲线提取方法。文献[6]结合Gabor时频分布和变分模态分解，来估计目标的自旋频率和锥旋频率；文献[7]利用短时分数阶傅里叶变换分离肢体和躯干的微多普勒信号。然而，由于时频分析法是基于基函数比较固定傅里叶变换理论，导致其缺乏自适应性或者自适应性差，在提取微多普勒信息时会存在一些不可避免的不足，难以同时保证时频分辨率以及避免交叉项[8]。

经验模态分解(empirical mode decomposition，EMD)没有固定的基函数，可以将目标回波信号分解为不同尺度的本征模态函数(intrinsic mode functions,IMF)，这些IMF一般具有明显的物理意义，表现了信号所包含的真实物理过程。在这过程中不存在人为干预，具有良好的自适应性[9]。但是在实际应用中，EMD算法并不完美，同样存在一些问题，如模态混合、端点效应等。为了解决模态混合问题，文献[10]通过加入不同有限振幅白噪声来辅助数据分析，提出了总体经验模态分解(ensemble empirical mode decomposition，EEMD)算法。

EEMD虽然大大减少了模态混叠现象，但其分解出的模态之和不能完美重构出目标信号，为了解决该问题，文献[11]在每一阶段的分解中都加入一个特定的白噪声，再通过计算残差得到该阶段的模态，提出了自适应噪声完备总体经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)算法，该算法实现了可以忽略的重建误差，并解决了加入的噪声不同时产生不同模态数量的问题。EMD及其衍生算法EEMD和CEEMDAN近些年来已广泛应用于微多普勒特征分析的研究中。文献[12]使用希尔伯特-黄变换对振动目标进行雷达微多普勒特征分析；文献[13]提出了一种基于经验模态分解的圆锥目标雷达微动特征提取方法；文献[14]通过对多目标回波信号进行CEEMDAN分解，结合小波阈值去噪方法，对各本征模态函数(IMF)进行分层处理并累加，分离出了弹头和碎片回波。

然而，CEEMDAN得到的IMF中仍含有一定的残留噪声，并且其中的信号信息出现得较晚，这些不足会极大地影响微多普勒特征提取的准确性和实效性。文献[15]通过将估计模态替换为估计局部均值，并将真实模态定义为当前残差与其局部均值的平均值之间的差值，提出了改进的自适应噪声完备总体经验模态分解(improved complete ensemble empirical mode decomposition with adaptive noise，ICEEMDAN)算法。本文针对CEEMDAN在微多普勒特征提取中存在的问题，提出基于ICEEMDAN的微多普勒特征提取方法。

1 改进的自适应噪声完备总体经验模态分解

定义Ek(·)为通过EMD获取第k个IMF的算子，k=1,…,K；M(·)为获取目标信号局部均值的算子；s(t)为目标的雷达回波信号，则：

E1(s(t))=s(t)-M(s(t))

(1)

ICEEMDAN算法通过将模态估计替换为局部均值估计，并将其从原始信号中减去，从而减少了模态中存在的噪声量。其算法的具体实现步骤如下：

步骤1 当i=1,2,…,I时，通过EMD分别计算s(i)(t)=s(t)+β0E1(w(i)(t))的I个局部均值，得到第一个残差为：

r1(t)=〈M(x(i)(t))〉

(2)

步骤2 计算第一个(k=1)IMF分量为：

(3)

步骤3 计算序列r1(t)+β1E2(w(i)(t))局部均值的平均值作为第二个残差，即：

r2(t)=〈M(r1(t)+β1E2(w(i)(t)))〉

(4)

并得出第二个IMF分量为：

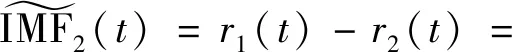
(5)

步骤4 当k=3,…,K时，计算出第k个残差为：

rk(t)=〈M(rk-1(t)+βk-1Ek(w(i)(t)))〉

(6)

步骤5 计算得出第k个IMF分量为：

(7)

步骤6 对于下一个k，转到步骤4。

重复步骤4到步骤6，直到获得的残差不能被进一步分解(即残差满足IMF的条件或者其极值小于等于2)。此时目标回波信号s(t)可以表示为：

(8)

2 基于ICEEMDAN的微动周期提取方法

空间进动锥体目标模型如图1所示，坐标系(U,V,W)为雷达坐标系，雷达静止于原点Q。O为目标质心，以O为原点，目标对称轴Oz为z轴建立目标本体坐标系O-xyz。以O为原点建立参考坐标系O-XYZ，以初始时刻与目标对称轴Oz、进动轴OZ共面且垂直于OZ的方向为Y轴，X轴根据右手准则确定。目标在平动的同时，以角速度ωs绕对称轴z轴做自旋运动，同时以角速度ωc绕轴OZ做锥旋运动(ωs和ωc均采用参考坐标系中的表达式)，自旋轴和锥旋轴之间的夹角为进动角θ。

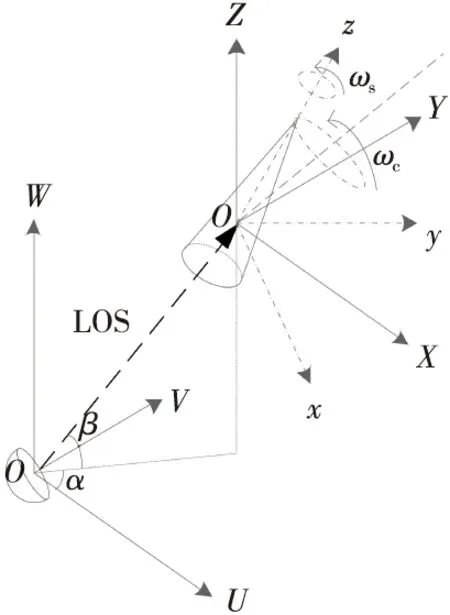
图1 进动目标模型Fig.1 Precession target model

在光学区，雷达目标的整体散射特性通常可以等效为若干个散射中心的叠加。不失一般性，假设目标的微动是周期性进动，目标等效为K个散射中心，各散射中心各向同性，雷达发射的电磁波为连续单频波，载频为f0。雷达向由i个散射点组成的目标发射电磁波，不考虑目标平动带来的影响，返回的基带信号可表示为：

(9)

式(9)中，λ是雷达载波波长，Ri是第i个散射中心到雷达原点的距离，σi(t)是第i个散射中心的散射强度，取决于目标的运动姿态。则第i个散射中心的瞬时微多普勒频率为：

(10)

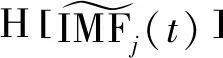
(11)

式(11)中，p表示柯西主值，则其解析信号Zj(t)可被构造为：

(12)

得到幅值函数和相位函数为：

(13)

从而可以求出其瞬时频率为：

ωj(t)=2πfj(t)=dθj(t)/dt

(14)

而由式(13)可看出，振幅和相位都是时间的函数，如果把振幅表示在时间—频率平面上，第j个IMF分量的希尔伯特时频谱为：

(15)

式(15)中，Re(·)是表示实部。目标回波信号s(t)的希尔伯特时频谱为：

(16)

式(16)可记为：

(17)

式(17)中，H(ω,t)精确地描述了回波信号的幅值随时间、频率的变化规律，通过对H(ω,t)的分析可进一步提取出目标的微多普勒特征。

3 仿真对比与分析

分别以ICEEMDAN算法和CEEMDAN算法对进动锥体目标回波信号进行分解，然后对得到的IMF进行希尔伯特谱分析，最后对比两种算法的提取效果，从而验证ICEEMDAN算法在微多普勒特征提取方面的性能提升。

仿真条件：假设雷达工作在10 GHz，且雷达坐标系中本体坐标系原点O的坐标为(400，500，100) km，本地坐标系和参考坐标系之间的初始欧拉角(x-y-z序列)为(30°，60°，45°)。假设目标绕z轴旋转，目标上有两个散射点：第一散射点A位于锥顶，在本体坐标系中的坐标为(0，0，1) m；第二个散射点B位于锥底的尾翼，在本体坐标系中的坐标是(0.5，0，-0.5) m。雷达照射时间为8 s，旋转频率为fs=1 Hz，圆锥运动频率为fc=0.5 Hz。

当不存在噪声时，基于CEEMDAN和ICEEMDAN的微多普勒特征提取结果分别如图2和图3所示，其中的频率都是取模后的频率，也就是正频率。图2(a)和图3(a)分别是两种算法获取的回波信号希尔伯特谱，展现了回波信号时频分布的细节；图2(b)和图3(b)分别是两种算法获取的IMF前三个分量的希尔伯特谱。

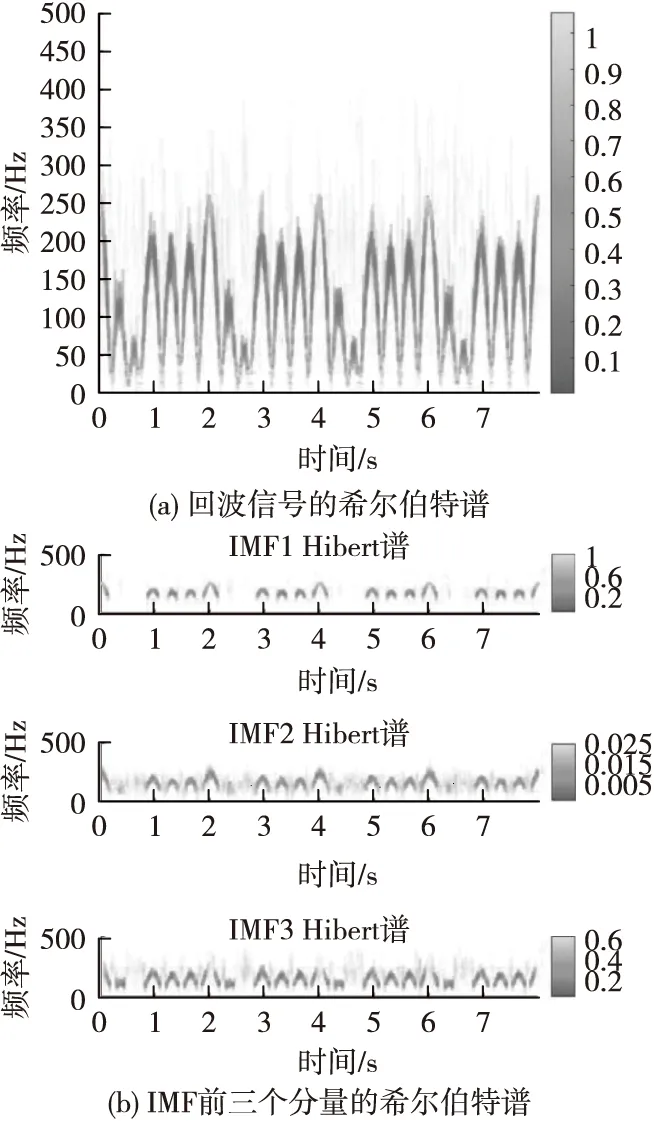
图2 基于CEEMDAN的估计结果(无噪声)Fig.2 Estimation result based on CEEMDAN (no noise)

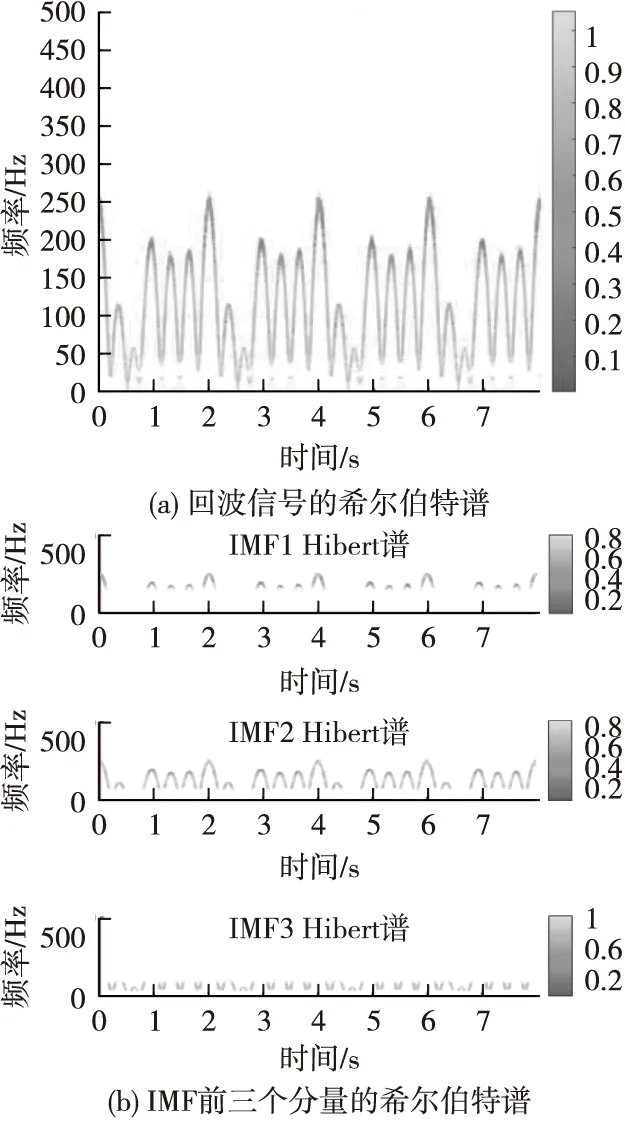
图3 基于ICEEMDAN的估计结果(无噪声)Fig.3 Estimation result based on ICEEMDAN (no noise)

由图2和图3可知，两种算法都能够准确提取出目标的微多普勒周期为2 s，这体现了两种算法都具备提取微多普勒特征的功能。但从图2中可以看到，在没有噪声的情况下，CEEMDAN的IMF中仍然残留着部分噪声。这些噪声是在在CEEMDAN算法的实现过程中，主动加入信号进行辅助分解的，但该算法却未能在分解过程中将所主动加入的噪声从IMF中清理掉，这势必会影响到微多普勒特征提取的准确性。而从图3可以看到，ICEEMDAN的IMF中不存在这些残留噪声，表明ICEEMDAN克服了CEEMDAN的这一不足。

当雷达回波信号中混杂着噪声时，同样的仿真条件下，假设信噪比SNR=5 dB，图4(a)为基于CEEMDAN的回波信号希尔伯特谱，图4(b)是基于CEEMDAN得到的IMF前三个分量的希尔伯特谱。

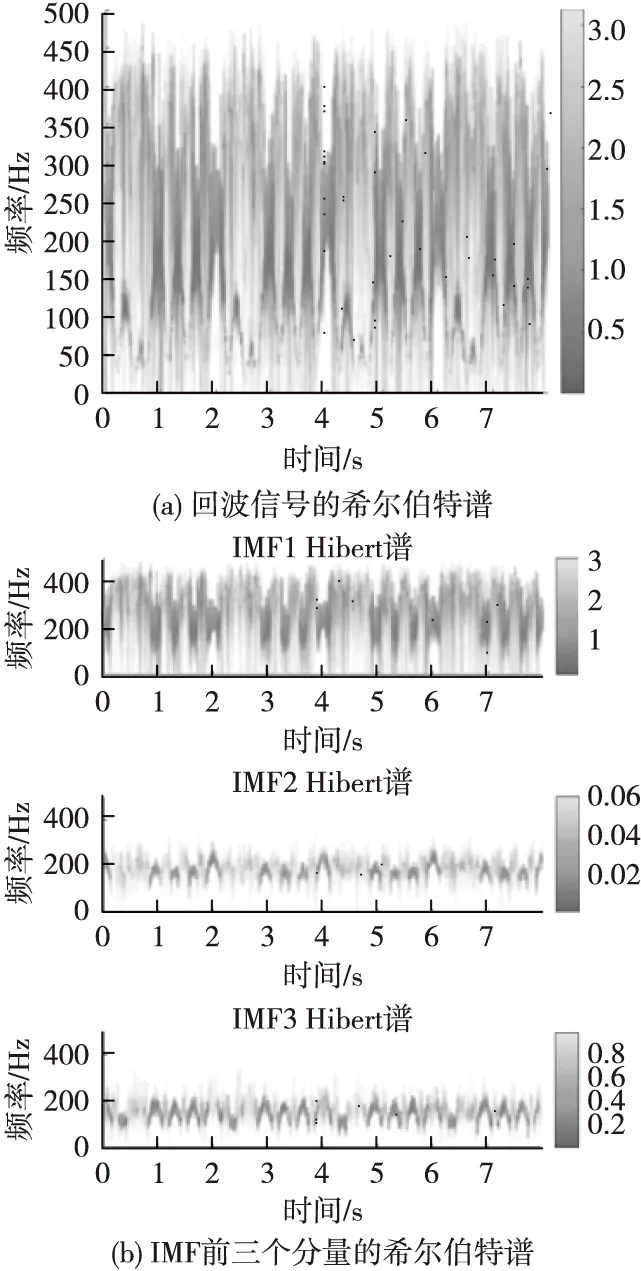
图4 基于CEEMDAN的估计结果(SNR=5 dB)Fig.4 Estimation result based on CEEMDAN (SNR=5 dB)

从图4(a)中可以看出，回波信号希尔伯特谱中的微多普勒频率伴随着大量的噪声频率，难以从中提取微多普勒特征。但以CEEMDAN将信号分解后，噪声主要集中于IMF第一个分量中，信号大部分被分解到IMF的第三个分量中，IMF第二个分量也包含了一部分的信号分量，如图4(b)所示，只能从IMF分量中提取微多普勒特征。

在其他条件不变的情况下，改用ICEEMDAN，图5(a)为回波信号的希尔伯特谱，图5(b)为其IMF前三个分量的希尔伯特谱。

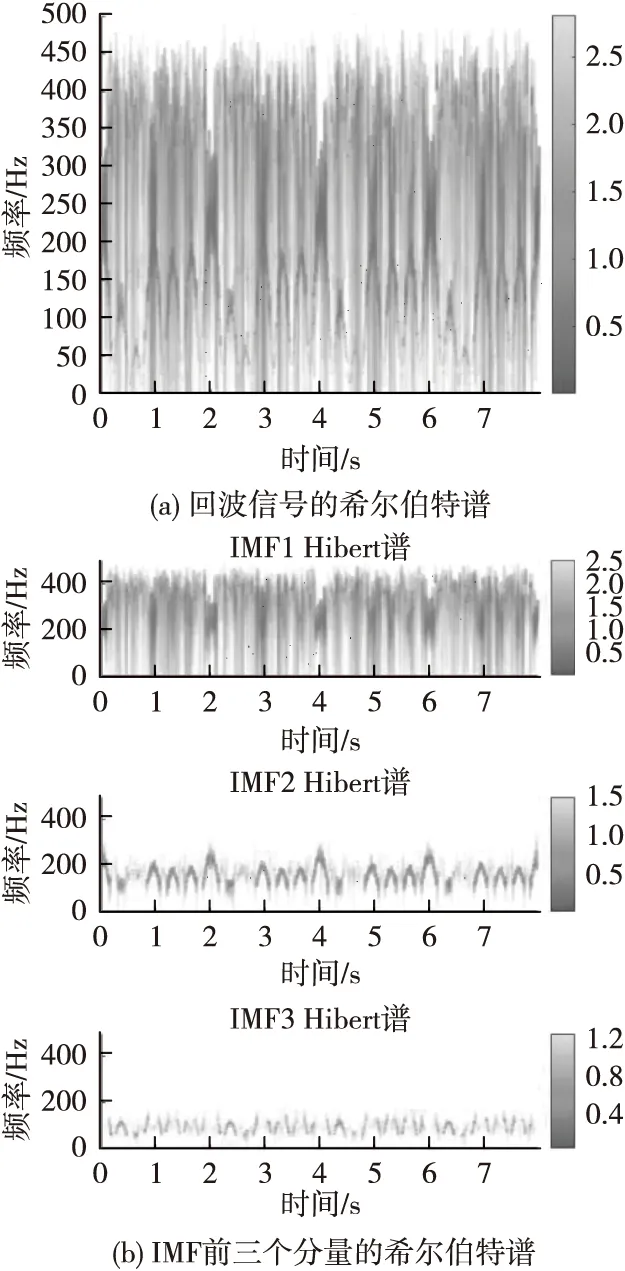
图5 基于ICEEMDAN的估计结果(SNR=5 dB)Fig.5 Estimation result based on ICEEMDAN (SNR=5 dB)

与图4(a)相似，同样难以从图5(a)提取微多普勒特征，此时也同样只能从图5(b)中的IMF分量中提取信息。但对比图5(b)和图4(b)，不难看出，CEEMDAN算法中的微多普勒信号大部分被分解在第三个分量中，而ICEEMDAN算法中的微多普勒信号则主要存在于第二个分量，即ICEEMDAN的信号信息出现得比CEEMDAN早。

进一步降低信噪比，图6(a)和图6(b)分别给出了信噪比为1 dB和0 dB时，基于ICEEMDAN得到的IMF前三个分量的希尔伯特谱。

图6 ICEEMDAN前三个IMF分量的希尔伯特谱Fig.6 Hilbert spectrum of the first three IMFs components of ICEEMDAN

由图6(b)可知，即使信噪比低至0 dB，仍能通过其第二个IMF分量的希尔伯特谱提取出微多普勒周期。这表明，在低信噪比环境中，ICEEMDAN具备良好的性能。

4 结论

本文提出基于ICEEMDAN的进动目标微多普勒特征提取方法，该方法以ICEEMDAN将进动目标回波信号分解为IMF，然后对IMF进行希尔伯特谱分析得到时频谱，用以估计目标的微动周期。仿真实验表明，该方法提取特征信息更快，实用性好，其IMF中的残余噪声较少，具备更好的抗噪性能。

本 刊 声 明

中国知网发起设立的“学术不端文献检测中心”,其功能是以《中国学术文献网络出版总库》和大量国际学术文献为全文比对资源,辅助检查抄袭、一稿多投、不当署名、伪造、篡改等学术不端行为。我刊作为中国知网的合作单位,有义务为净化学术空气,制止学术不端行为作出贡献,请各位读者、作者大力支持,与我们共同努力,从根本上铲除学术腐败的土壤,树立全民求真、求实的科学态度。

本刊编辑部