基于双分支网络和特征融合的雷达欺骗干扰识别

王奇伟，孙闽红，仇兆炀

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

0 引言

雷达电子对抗(ECM)和雷达电子反对抗(ECCM)是电子战的两个主要分支，它们在相互作用、互相联系中快速发展[1]。雷达有源欺骗干扰作为一种高效灵活的电子对抗技术，随着数字射频存储器(DRFM)的发展得到了广泛的应用。目前有源欺骗干扰识别的现有研究成果主要可以分为传统方法和智能方法，传统方法主要是对欺骗干扰信号提取到的特征通过分类器进行分类识别，而智能方法是将雷达接收信号直接输入给深度学习网络进行分类识别。文献[2]针对线性调频相参雷达抗自卫欺骗干扰问题，基于回波相关差异提出了一种经典时频相关移频干扰识别方法和一种尺度时频相关移频的干扰识别方法。文献[3]针对真假目标在不同域的特征表现差异，将提取的空、频域特征在时域上融合，最后用判别器和二元假设检验算法完成提距离—速度复合欺骗干扰的识别。文献[4]针对三种常见的欺骗干扰进行双谱分析，经过降维和归一化处理后，将三维双谱信息转化为二维特征信息，对得到的二维特征谱提取熵特征和盒维数组成特征参数集放入分类器中进行分类识别。文献[5]对雷达接收信号进行时频分析后通过Zernike矩特征提取时频图像的细节特征组成特征向量进行分类识别。

随着深度学习网络表现出较强的非线性拟合和自学习能力，不少研究人员也将神经网络应用于欺骗干扰识别。文献[6]对干扰下的雷达接收信号进行时频分析，用栈式稀疏自编码器对时频特征进行降维，最后利用Softmax分类器完成有源欺骗干扰的识别。文献[7]基于统一格式干扰数据集采用卷积神经网络实现干扰的监督学习。传统方法的不足在于所提特征只适用于特定欺骗干扰类型的识别，而现有的智能识别方法仅将雷达接收信号的时频图作为输入数据进行欺骗干扰识别，丢失了信号的相位信息导致识别率不高。综上所述，现有方法均未充分利用雷达接收信号的信息，因此本文提出基于双分支网络和特征融合的雷达欺骗干扰识别方法。

1 相关基础知识

1.1 转发式欺骗干扰信号模型

转发式欺骗干扰是指干扰机通过DRFM对截获到的雷达信号进行幅度、时延、多普勒频率等调制后转发的欺骗干扰信号。本文主要对距离欺骗干扰、速度欺骗干扰、距离-速度同步欺骗干扰以及密集假目标干扰的类型识别。不失一般性，雷达发射信号以线性调频信号(LFM)为例，则其可以表示为：

S(t)=Aexp(φ(t)+jφ0)

(1)

式(1)中，A是发射信号的幅度，φ(t)=jπ(2f0t+kt2)，f0为中频频率，k为调频斜率，φ0为发射信号的初始相位，j是虚数单位。假如与雷达相距R0的位置处有一个目标，则此时雷达接收机接收到的真实信号为：

ST(t)=AT·exp(φ(t-tT)+jφ0)

(2)

式(2)中，AT为目标信号的幅度，tT=2R0/c，c为光速，即c=3×108m/s。

距离假目标欺骗干扰是DRFM干扰设备对干扰脉冲的转发时延进行调制，使得干扰脉冲和目标回波分别位于不同的距离门，达到对雷达的距离欺骗干扰效果。则当DRFM干扰机转发距离假目标欺骗干扰时，雷达接受机接收到的信号为：

JR(t)=AT·exp(φ(t-tT)+jφ0)+
AR·exp(φ(t-tr-tj)+jφJ)

(3)

式(3)，AR为距离欺骗干扰的幅度，tj为距离欺骗干扰的时延调制值，φJ为干扰信号的初始相位。

当DRFM干扰机转发速度假目标欺骗干扰时，雷达接受机接收到的信号为：

JV(t)=AT·exp(φ(t-tT)+jφ0)+
AV·exp(φ(t-tr)+jφJ)·exp(-j2πfJ)

(4)

式(4)中，AV为速度假目标欺骗干扰的幅值，fJ为速度假目标欺骗干扰的多普勒频移调制值。

当DRFM干扰机转发速度假目标欺骗干扰时，雷达接受机接收到的信号为：

JRV(t)=AT·exp(φ(t-tT)+jφ0)+
ARV·exp(φ(t-tr-tj)+jφJ)·exp(-j2πfJ)

(5)

本文选择频谱弥撒(SMSP)干扰作为密集假目标的干扰样式，其干扰产生的主要思路是：在干扰机截获到空间中的雷达发射信号时，对截获的雷达信号进行时域压缩，得到的干扰子脉冲的时宽是截获信号的1/n，而设置干扰信号的调制斜率为捕获信号的n倍，然后将干扰信号的子脉冲复制n段就可以得到SMSP干扰。

SMSP干扰首先产生一个子波，其信号模型可以表示为：

J1(t)=AJexp(jπk′t2),k′=nk,0≤t≤T/n

(6)

式(6)中，AJ代表SMSP干扰信号的幅度；k′表示干扰信号的调频斜率，为雷达发射信号调频斜率k的n倍，则干扰的子脉冲时宽变为雷达发射信号脉宽的1/n。

然后将J1(t)重复n次，得到整个SMSP干扰的时域模型为：

(7)

式(7)中，⊗是卷积算子，δ(t)是冲激函数。

1.2 雷达接收信号的时频图和时相图

Wigner-Ville分布[8](WVD)是最基础的时频分析方法，其他所有时频分析方法都可以看作是在它的基础上做了加窗处理，其定义为：

(8)

式(8)中，局部相关函数Rz(t,τ)=z(t+τ/2)·z*(t-τ/2)，τ是时滞，式(8)也可以称为信号z(t)的双线性变换。但是由于它的双线性，多个信号混叠后WVD中会出现交叉项。修正的平滑伪Wigner-Ville分布(MSPWVD)对时频分布必然存在的交叉项可以有效地抑制，其定义为：

(9)

式(9)中，g(t)h(τ)是窗函数，即对t和τ分别加g(t)和h(τ)作平滑。当对SPWVD分布进行适当的“重排”后，会丢失双线性但是能够保留WVD的其他性质不丢失，所以分布的性能会有进一步的提高，并把重排后的SPWVD分布称为修正的伪平滑伪Wigner-Ville分布(MSPWVD)，即有

(10)

取式(10)的幅值信息作为时频图(TFD)、相位信息作为时相图(TPD)，以真目标回波信号为例给出雷达接收信号的时频图和时相图，如图1所示。

图1 雷达接收信号的时频图和时相图(SNR=4 dB)Fig.1 TFD and TPD of received radar signal(SNR=4 dB)

1.3 特征融合

典型关联分析(canonical correlation analysis， CCA)[9]算法是将两组高维数据降维到一维，然后使用相关性分析，使得两组数据投影后的相关性最大[10]。但是CCA等算法的局限性在于仅计算了多个特征向量在某一方向上达到相关性最大，而忽略了数据集的类间信息，文献[11]提出了判别相关分析(DCA)算法，该算法最大化相同类别特征集之间相关性的同时，最小化了不同类别特征集之间的相关性，进一步提高了分类性能。以下给出DCA算法步骤：

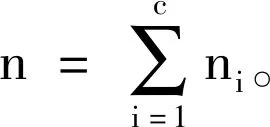
类间散度矩阵定义为：

(11)

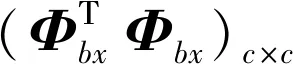
(12)

(13)

由式(13)可知，Sbx最大的r个特征向量可以通过将矩阵Q进行映射得到，即Q→ΦbxQ。

(ΦbxQ)TSbxΦbxQ=Λ(r×r)

(14)

令Ηbx=ΦbxQΛ-1/2，则类间散度矩阵Sbx被转化为单位矩阵，并将特征矩阵X的维数从p降为r。

(15)

(16)

式(16)中，X′是X在空间中的投影。

将式(11)代入式(15)可得：

(17)

同理，从时相图样本集中提取的特征矩阵Y通过变换后得到的投影矩阵可以表示为：

(18)

(19)

式(19)中，Y′是Y在空间中的投影，r为特征矩阵投影后的特征维度，r≤min(c-1,rank(X),rank(Y))。

上述已经将时频特征矩阵X和时相特征矩阵Y投影到了X′和Y′，将类间散度矩阵单元化，使得不同类之间具有最小相关性。要使同一样本对应的特征矩阵X′和Y′之间具有最大相关性，先求出二者之间的协方差矩阵S′xy=cov(X′,Y′)，然后对S′xy进行奇异值分解：

S′xy(r×r)=UΣVΤ⟹UΤS′xyV=Σ⟹
(UΣ-1/2)TS′xy(VΣ-1/2)=I

(20)

令Hcx=UΣ-1/2和Hcx=VΣ-1/2，得到：

(21)

(22)

最后将降维后的投影特征矩阵级联或求和：

(23)

或

(24)

2 基于双分支网络和特征融合雷达欺骗干扰识别

2.1 双分支CNN网络模型

为了解决现有欺骗干扰识别方法中对雷达接收信号做时频分析后，仅将时频图作为训练样本利用神经网络进行分类识别的方法，对雷达接收信号的信息特征提取不够完善这一缺点，本文设计了一种双分支网络来提取雷达接收信号的时频图和时相图特征，其网络框架如图2所示。

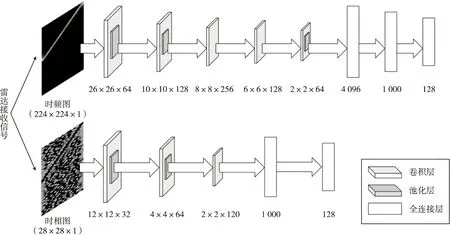
图2 双分支网络框架Fig.2 The dual branch network framework

如图2所示，双分支网络的上分支是一个AlexNet网络[12]，其输入大小为224×224×1的图片，隐藏层总共分为8层，其中有5个卷积层，3个全连接层，其中5个卷积层中的卷积核大小分别为11×11、5×5和3×3，全连接层的大小分别为4 096、1 000和128；下分支是一个LeNet-5网络[13]，其输入大小为28×28×1，有3个卷积层，2个全连接层，其中卷积核的大小均为5×5，全连接层的大小分别为1 000和128。

2.2 GDCA特征融合算法

考虑到DCA算法中的类间散度矩阵是将每一类特征向量的平均值与所有类特征向量的平均值做差运算，不能有效地降低类间的相关性，因此，本文基于双分支网络模型提出了改进的DCA算法——高斯判别相关算法(Gauss discriminant correlation analysis，GDCA)算法，该算法通过引入高斯函数重新定义了类间散度矩阵，增加了类间差异较小的距离，适当减少了类间差异较大的距离，改进了类别数较少时的分类性能。

为此，本文所提GDCA算法重新定义了DCA算法中的类间散度矩阵：

Sbx(p×p)=[θ1,θ2,…,θc][θ1,θ2,…,θc]T

(25)

2.3 基于双分支网络和特征融合的欺骗干扰识别算法步骤

基于双分支网络和特征融合的欺骗干扰识别方法步骤如下：

1) 利用预训练的双分支网络，分别提取训练集中雷达接收信号时频图和时相图的深度特征向量，构成深度特征矩阵Xp×n=[φ1,φ2,…,φn]和Yq×n=[ξ1,ξ2,…,ξn]；

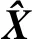
3) 根据式(23)或式(24)融合得到最终的特征矩阵Z，并用来训练SVM分类器；

3 仿真实验与分析

为了验证基于双分支网络和特征融合算法的有效性，利用雷达接收信号中是否存在距离假目标欺骗干扰、速度假目标欺骗干扰、距离-速度同步假目标欺骗干扰和密集假目标干扰进行仿真实验。雷达发射信号参数如下：发射信号调制类型为LFM，载频为10 GHz，脉宽为20 μs，信号带宽为10 MHz，采样频率为40 MHz，脉冲重复间隔为100 μs；距离假目标欺骗干扰产生的干扰时延为2 μs；速度假目标欺骗干扰产生的多普勒频偏是2 kHz；距离-速度同步欺骗干扰叠加了距离和速度欺骗干扰的干扰效果；SMSP干扰的采样倍数为4；干信比为6 dB。上述4种欺骗干扰类型和真目标回波信号各产生800个，每种类型信号随机抽取600个信号作为训练集，剩下的样本作为测试集。实验都是在一台CPU为Intel(R) Core(TM) i7-8750H 2.20 GHz，GPU为NVIDIA GeForce GTX 1060MaxQ的电脑上运行，内存为16 GB，硬盘容量为512 GB的固态硬盘，所有数据仿真产生都是通过Mtalab 2018a编程实现。

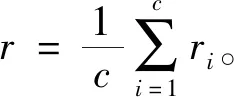
3.1 本文方法欺骗干扰的识别性能验证实验

为了验证本文方法对于雷达欺骗干扰样式分类识别的性能，需要评估该方法识别结果受信噪比的影响程度。首先利用大量样本对所提双分支网络进行预训练，利用得到的预训练网络对测试样本进行特征提取，然后根据所提改进的GDCA算法将所提特征矩阵进行空间投影映射，将融合后类间相关性更小、类内相关性更大的特征矩阵送入SVM分类器进行干扰识别。预训练的双分支网络结构如图2所示，其进行训练时的参数设置为：初始学习率设置为0.000 1，batch_size为100，使用交叉熵作为损失函数，优化器为Adam。将雷达接收信号的信噪比按照0～10 dB递增，每个信噪比下实验重复50次，得到本文方法对于欺骗干扰样式分类识别的结果如图3所示。

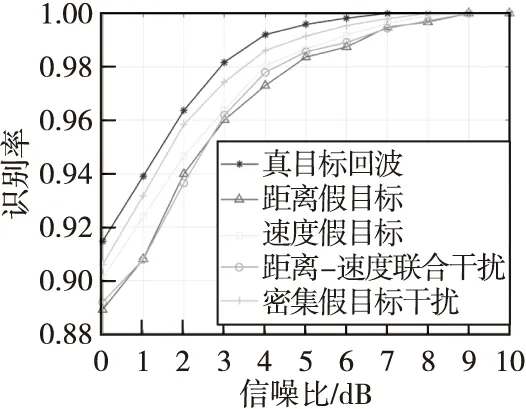
图3 本文方法的识别率变化曲线Fig.3 Identification probability curve of this paper method

从图3可以看出，本文方法对于欺骗干扰的平均识别率整体来说在信噪比大于0 dB时已经超过90%，并且在信噪比大于8 dB时，平均识别率接近100%。由于真实目标的识别率自始至终都高于欺骗干扰假目标，所以该方法可以很好地区分信号是否受到欺骗干扰，密集假目标干扰相比较在时频图和时相图上与真目标的差异最大，因此其识别率很高；速度假目标欺骗干扰与真目标的差异主要在于多普勒频移差异，导致其识别率不高；而距离-速度联合假目标与距离假目标欺骗干扰的识别率很接近是因为二者在时频图和时相图上的差异较小。

3.2 不同条件下的欺骗干扰识别率对比实验

为了验证引入雷达接收信号时相图能否提高欺骗干扰的识别率，首先仅将雷达接收信号的时频图进行干扰识别，同时为了保证实验可靠性，利用双分支网络中用来提取时频图特征分支的AlexNet网络对欺骗干扰进行识别；然后再同时将时频图和时相图利用双分支网络进行识别，此时双分支网络提取的特征向量只进行简单的串联拼接；最后，为了验证所提特征融合算法在前述的基础上对干扰识别率改进效果，利用前述预训练好的双分支网络提取雷达接收信号的时频图和时相图特征矩阵，然后利用GDCA算法将所提特征矩阵进行空间投影映射，将融合后类间相关性更小、类内相关性更大的特征矩阵送入SVM分类器进行干扰识别。将雷达接收信号的信噪比按照0～10 dB递增，每个信噪比下实验重复50次，取平均识别率作为最终识别结果，不同条件下欺骗干扰信号的识别结果如图4所示。

图4 不同条件下的欺骗干扰识别性能对比Fig.4 Jamming recognition performance comparison under different conditions

从图4可以看出，仅用雷达接收信号的时频图进行欺骗干扰识别时，识别率随着信噪比的增加而提高，当信噪比≥8 dB时，识别率接近100%；而当同时引入雷达接收信号的时相图进行干扰识别，信噪比≥7 dB时，识别率接近100%，相较于仅利用时频图进行干扰识别的识别效果平均提高了1.49%，证明了本文提出将时频图和时相图同时进行干扰识别的可行性和有效性；在此基础上引入特征融合算法后的欺骗干扰平均识别率更是提高了3.42%，说明所提特征融合算法能够有效地改善欺骗干扰识别性能。

为了增加算法性能分析的客观性和可靠性，对不同条件下的算法计算效率进行分析。在测试集样本随机抽取100个样本，分别用已训练好的模型进行预测，最后对总耗时取平均值，得到不同条件下的算法计算效率如表1所示。

表1 不同条件下算法计算效率对比Tab.1 Comparison of algorithm calculation efficiency under different conditions

如表1所示，仅用时频图进行欺骗干扰识别时所用AlexNet网络的平均耗时为139 ms，而将时频图和时相图同时输入至双分支网络时模型平均耗时为145 ms，在此基础上加入特征融合算法后，模型平均耗时为148 ms。综上可知，本文所提方法在识别率上有所提高，但算法计算效率略有降低，具体表现为毫秒量级。因此，总体上讲本文算法性能有所改善。

3.3 不同特征融合算法的识别性能对比实验

为了验证改进的DCA算法——GDCA特征融合算法对干扰识别的有效性，利用预训练的双分支网络提取训练样本的特征向量，然后分别采用CCA算法和DCA算法以及本文所提算法对特征进行融合，最后将融合后的特征用SVM分类器进行干扰分类识别，识别结果如表2所示。

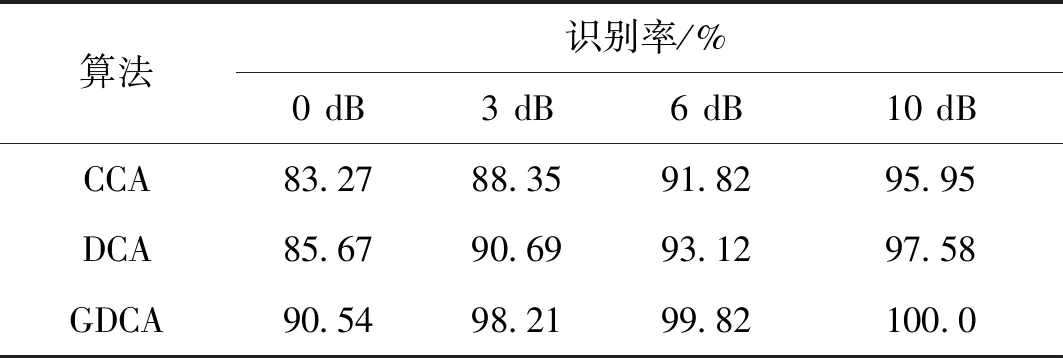
表2 不同特征融合算法的识别性能比较Tab.2 Recognition performance comparison of different feature fusion algorithms

由表2可以看出，本文所提GDCA算法性能优于DCA算法，这主要是因为DCA算法在类别数量较少时，式(25)在对角化矩阵后只取非零特征值组成的特征向量维数较低，使得融合性能较差。而GDCA算法在定义类间散度矩阵时引入高斯函数，进一步增加了不同类间的特征向量之间的差异，使得对角化矩阵后的特征值为零的概率降低，有效地改进了DCA算法的特征融合性能。

3.4 所提方法与现有文献的识别性能对比实验

为了验证本文方法的优越性，将本文结果和文献[4]和文献[6]作比较。为了保证实验结果的可靠性，实验中各参数设置均与原文献一致，且三种算法使用相同的数据集。将雷达接收信号的信噪比按照0～10 dB递增，每个信噪比下实验重复50次，取平均识别率作为最终识别结果，不同算法下的识别结果如图5所示。

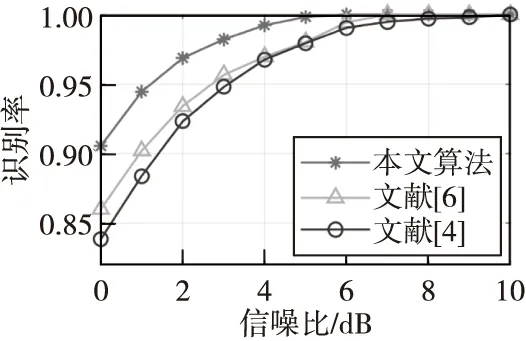
图5 3种方法识别率比较Fig.5 Recognition performance comparison of three kinds methods

从图5可以看出，本文所提方法的识别效果受信噪比的影响最小，识别性能最好，在SNR≥0时识别率就达到了90%，并且在SNR≥6 dB时识别率接近100%；相较于文献[6]平均提升了1 dB，而相较于文献[4]平均提升了2 dB，实验证明本文所提方法合理引入雷达接收信号的相位信息，并通过GDCA算法将时频图和时相图中的特征有效融合，有利于改善欺骗干扰识别性能，突出了该方法的优越性。

4 结论

本文提出一种基于双分支网络和特征融合的雷达欺骗干扰识别方法，该方法首先对雷达接收信号进行了时频分析，然后利用双分支网络提取了时频图和时相图中的高维特征，并利用GDCA算法对提取的特征矩阵进行映射和降维，使得融合后的特征矩阵具有类内最大相关性、类间最小相关性，最后输入到SVM分类器中完成雷达欺骗干扰样式识别。仿真实验表明，将所提方法与仅使用神经网络提取雷达接收信号时频图特征进行欺骗干扰识别的方法进行对比，所提方法的识别性能有所改善，证明了引入时相图进行雷达欺骗干扰识别的可行性和有效性。