Cu含量对γ-Ni相影响的第一性原理

李亚敏,江 璐,刘洪军

(兰州理工大学 部共建有色金属先进加工与再利用国家重点实验室,甘肃 兰州 730050)

镍基高温合金具有的优点与镍自身的优异性能有关[1].镍为面心立方结构,组织非常稳定,从室温到高温不发生同素异型转变；镍具有高的化学稳定性,在500℃以下几乎不氧化,常温下也不受湿气、水及某些盐类水溶液的作用.镍在硫酸及盐酸中溶解很慢,而在硝酸中溶解很快；纯镍的硬度虽然不高,但塑性却极好,尤其在低温下塑性变化不大；Ni原子的电子排布式为1s22s22p63s23p63d84s2,第三电子层基本达到饱和,因此镍具有比较大的合金化能力,甚至添加十几种合金元素也不出现有害相,这就为改善镍的各种性能提供了可能.因此,研究人员经常采用合金化的方法来提高镍基合金的性能[2-4].近年来,随着计算材料的不断发展,从固体物理的角度研究合金元素的掺杂问题成为了热点[5].王云江[6]采用基于密度泛函理论(DFT)的第一性原理贋势平面波方法研究了合金元素Ta、Mo、W、Cr、Re、Ru、Co以及Ir对γ-Ni相弹性性质的影响,并对各计算模型的晶格常数、弹性模量以及韧脆性进行了分析.结果表明,除Co和Cr外,其余合金元素均使γ相的晶格常数增大,并且所有合金元素的加入都降低了γ相和γ′相之间的晶格错配度；除了Co以外,其余的合金元素均使γ相的脆性变大.

Cu作为镍矿的伴生元素,对镍基合金组织和性能具有重要的影响[7].因此,研究Cu对镍基合金基体γ相的影响具有现实意义.本文采用第一性原理计算的方法从微观电子结构入手,研究四种不同浓度Cu的掺杂对γ-Ni相结构稳定性、弹性力学性质以及电子结构的影响；并结合实验分析Cu的含量对铸态Inconel 718合金γ相力学性能的影响.

1 模型建立与试验方法

1.1 计算方法与晶体模型建立

γ-Ni相属面心立方结构,空间群为FM-3M,晶格常数a=b=3.571 8×10-4μm,α=β=γ=90°[8].分别构造由8个、16个和32个原子组成的Ni (1×2×1)、(2×2×1)和(2×2×2)超晶胞,将一个Cu原子掺杂进超晶胞体系中,得到的超晶胞计算模型如图1所示.由于Cu在镍原材料中的含量有限,因此只考虑一个Cu原子掺杂的情况.当超晶胞模型为Ni8、Ni31Cu、Ni15Cu和Ni7Cu时,所对应Cu原子的掺杂原子分数分别为0%、3.125%、6.25%和12.5%.

计算采用基于密度泛函理论(DFT)的贋势平面波CASTEP(cambridge serial total energy package)程序,平面波截断能取400 eV,Ni8和Ni7Cu的K点网格数取12×6×12,Ni31Cu的取6×6×6,Ni15Cu的取6×6×12.采用广义梯度近似(GGA)处理交换关联能部分,交换关联势取Perdew-Wang91 (PW91)形式.Ni原子的3d84s2和Cu原子的3d104s1作为价电子,其他轨道电子视为芯电子.计算之前采用BFGS方法对计算模型进行结构优化.自洽计算参数为：总能量收敛设为2.0×10-6eV/atom,每个原子上的力低于5×106eV/μm,公差偏移小于2×10-7μm,应力偏差小于0.1 Pa.

1.2 实验方法

以铸态Inconel 718合金为研究对象,分析Cu元素的含量对合金基体相γ-Ni相的影响.铸态Inconel 718合金基体相以γ相为主.实验原材料的化学配比见表1.试样制备过程为配料-混料-压块-熔炼-切割.采用HBRVU-187.5型布洛维氏光学硬度计测试实验合金的布氏硬度.测试前试样表面经240#～800#水砂纸逐级打磨,每个试样测试5个点,取平均值.屈服强度测试采用的设备为WDW-100D型电子万能材料试验机,试样尺寸为φ5 mm×8 mm,压缩实验前试样表面经600#砂纸机械磨光.采用JEM-6700F场发射扫描电子显微镜观察合金晶界析出相的大小、形貌及分布,化学腐蚀剂成分为：

1g CuSO4+ 20mL HCl + 10mL C2H5OH

图1 γ-Ni体系的超晶胞计算模型 Fig.1 Supercell model of γ-Ni

表1 实验合金的化学成分(质量分数)

2 结果与讨论

2.1 形成热与结合能

为了判断Cu原子掺杂γ-Ni体系后对其稳定性的影响,分别计算了各掺杂模型的形成热与结合能.计算结果见表2.

表2 掺杂前后γ-Ni体系的形成热和结合能

形成热用来衡量相结构的稳定性.Cu掺杂进γ-Ni体系后,形成热的计算公式如式(1)所示：

(1)

晶体的强度、结构稳定性与其结合能密切相关,结合能的绝对值越大,则形成的晶体越稳定.Cu原子掺杂进Ni体系后,结合能的计算公式如式(2)所示：

(2)

由表2可知,各计算模型的形成热和结合能均为负值,表明各晶胞结构均能够形成,并且形成的结构相对稳定.各计算模型形成热的绝对值随着Cu掺杂浓度的升高而降低,表明未掺杂Cu原子的晶胞结构最易形成,当掺杂原子分数为12.5%时,其晶胞相对于其他晶胞结构而言较难形成.各计算模型结合能的绝对值均随着掺杂浓度的升高而降低,表明未掺杂Cu原子的晶胞最稳定,随着掺杂浓度的增加,晶胞结构的稳定性依次降低.综合分析形成热和结合能可知,Cu原子的掺杂降低了γ-Ni体系的结构稳定性.体系稳定性的降低促使铸态Inconel 718合金的组织形貌发生了显著的变化,合金中析出了大量的Laves相[9],如图2所示.

2.2 弹性性质

弹性常数Cij可以描述晶体的弹性性质.在线弹性近似下,当应变分量趋近于0时,由胡克定律可知,每一个应力分量都可以表示成6个应变分量的线性函数,如式(3)所示：

σij=cijklekl

(3)

式中:Cijkl为弹性常数,是一个9×9的四阶张量,可以简化为Cij,用6×6的矩阵表示9×9的矩阵[10].

对于立方晶系而言,只有三个独立的弹性常数,分别为：C11、C12以及C44,其力学稳定性判断条件为[11-14]

C11>0,C44>0,C11-C44>0,C11+2C12>0

(4)

对于四方晶系而言,有六个独立的弹性常数,分别为C11、C12、C13、C33、C44和C66,其力学稳定性判断条件为

(5)

分别计算不同Cu掺杂浓度体系Ni8、Ni31Cu、Ni15Cu和Ni7Cu的弹性常数,结果见表3.从表3可以看出,计算获得的弹性常数值与实验值和其他理论计算值比较接近,说明所构建的计算模型和计算方法合理.立方结构的Ni31Cu计算模型满足力学稳定性(4)的条件,四方结构的Ni8、Ni15Cu和Ni7Cu的计算模型均满足式(5)的力学稳定性条件,表明掺杂前后各体系都是力学稳定的.比较均为四方体系的Ni8、Ni15Cu和Ni7Cu的计算结果可知,掺杂体系的弹性常数随着Cu原子掺杂浓度的增大而减小.

表3 掺杂前后γ-Ni体系的弹性常数Cij

为了进一步讨论Cu的掺杂对Ni体系弹性力学性质的影响,对各掺杂体系体模量B、剪切模量G、G/B以及杨氏模量E的值进行了分析.晶体的体模量B和剪切模量G都可以由晶体的弹性常数通过Voigt-Reuss-Hill近似推算出来,其中Voigt、Reuss和Hill分别表示弹性系数的最大值、最小值和平均值.

对于立方晶系而言,体模量和剪切模量可以简化成如下计算公式[14]：

对于四方晶系而言,体模量和剪切模量可以简化成如下计算公式：

对于所有晶系,杨氏模量E的计算公式如下：

(12)

体模量与剪切模量都是弹性模量的一种表征,体模量是材料对于表面四周压强产生形变的度量,与材料中原子间的综合性质有关.通常用来描述材料在外力作用下的抗体积变形能力,其值越大说明晶体的抗变形能力越强.剪切模量可以判断材料在剪切应力作用下的抗变形能力.剪切模量越大,说明材料原子间的定向键越明显.杨氏模量是用来衡量固体材料硬度的弹性模量.杨氏模量越大,说明固体材料的硬度就越大[15].

由公式(6～12)计算各掺杂体系体模量B、剪切模量G、G/B以及杨氏模量E,结果见表4.从表4可以看出,当Cu原子的掺杂质量分数为0%时,所对应的掺杂体系Ni8的弹性模量值最大；Cu原子掺杂进γ-Ni体系后,使得各掺杂模型的体模量B、剪切模量G以及杨氏模量E均有不同程度的降低,其中剪切模量G随着Cu掺杂质量分数的增大而依次降低.对Cu掺杂前后体系弹性模量的分析可知,Cu的掺入降低了体系的硬度和抗体积变形能力,使原子间的定向键与结合能力减弱.

表4 掺杂前后γ-Ni体系的体模量B、剪切模量G、B/G以及杨氏模量E

为了分析Cu的掺杂对γ-Ni体系延性的影响,通过Pugh判据进行了计算[16].Pugh判据的基本标准为：材料的延性可以用剪切模量G与体模量B的比值来表征,材料延性和脆性的临界值为0.57,当G/B<0.57时,材料具有延性；当G/B>0.57时,材料为脆性.并且G/B的值越小,材料的延性越好.反之,材料的脆性越大.各掺杂模型G/B的值见表4,从表4可以看出,掺杂前后各计算模型G/B的值均小于0.57,表明Cu掺杂前后各体系均具有延性,并且随着Cu的掺杂,G/B的值有不同程度的升高,表明Cu的掺杂降低了体系的延性.综合考虑Cu的掺杂对体系弹性模量的影响可知,Cu降低了体系的弹性力学性能.计算结果在实验中也获得了证实.图3为不同Cu含量铸态Inconel 718合金的硬度和屈服强度图.从图3可以看出,0号合金的硬度最高,随着Cu的加入铸态合金的硬度依次降低；未加入Cu的合金屈服强度值最高,随着Cu的加入铸态合金的屈服强度依次降低,变化趋势与硬度相同.实验结果进一步证实了计算模型和计算方法的合理性.

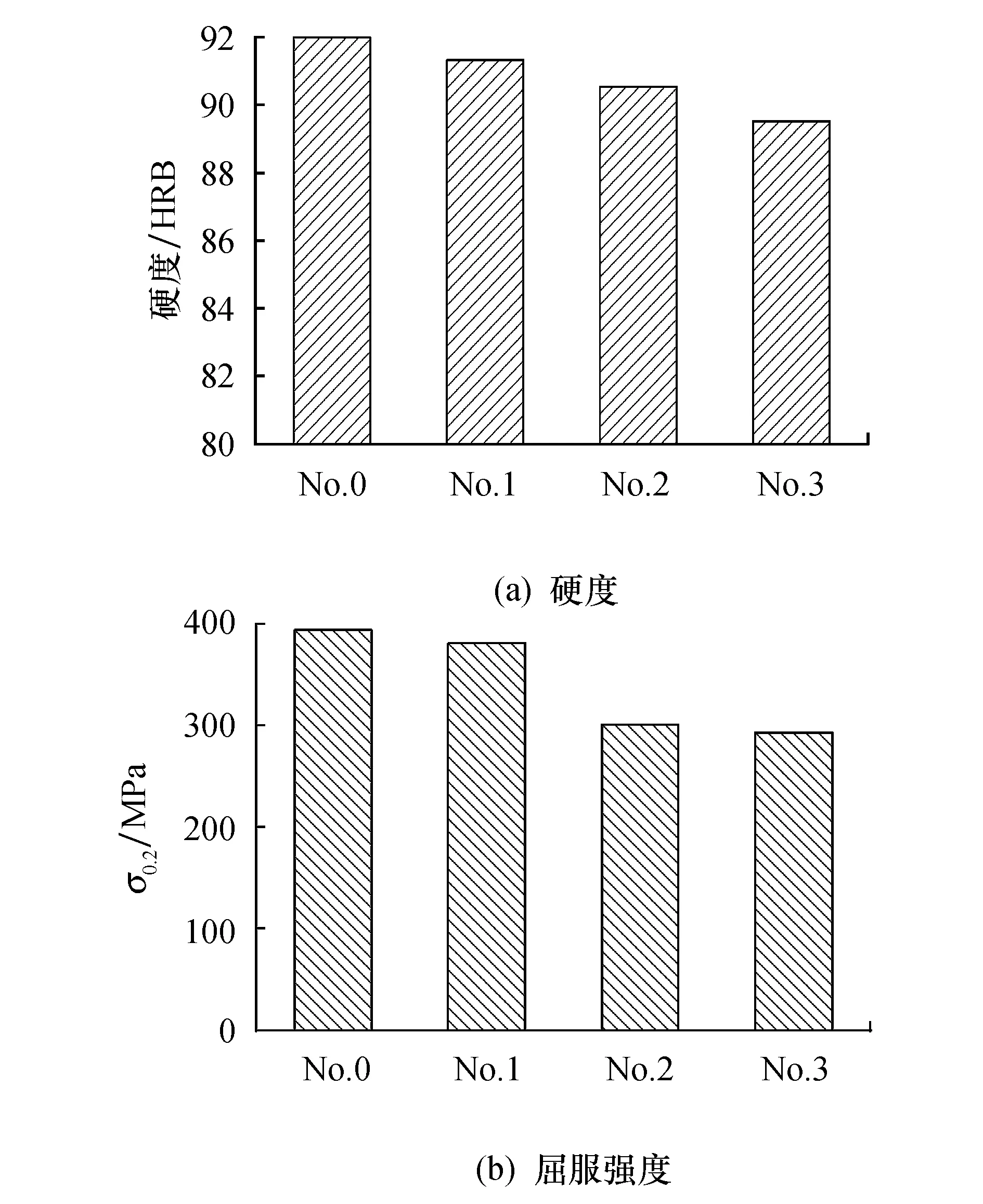
图3 铸态Inconel 718合金的硬度和屈服强度Fig.3 Hardness and yield strength of as-cast 718 alloy

2.3 态密度

从计算和实验结果可以发现,Cu原子掺杂进γ-Ni体系后使其结构稳定性与弹性力学性能均降低,为了进一步从电子结构上分析造成这一变化的本质原因,选取Cu原子掺杂前后掺杂质量分数分别为0%和12.5%的Ni8与Ni7Cu掺杂体系进行总态密度(DOS)和分波态密度(PDOS)计算分析.计算中所涉及到的原子外层电子结构包括Ni 3d84s2和Cu 3d104s1,计算结果如图4所示.从各掺杂模型的DOS图中可以看出,掺杂前后计算模型费米能级处的电子浓度均不为零,说明掺杂前后体系均呈现明显的金属性.并且掺杂前后,成键电子的分布情况基本不变,均处在为-10～-12 eV.从图4a可以看出,Ni8模型的成键电子主要是由Ni d轨道和少量的Ni p轨道贡献,并且在费米能级处有个很大的尖峰；从图4b可以看出,Ni7Cu模型的成键电子主要是由Ni d轨道和Cu d轨道贡献,这些电子轨道在费米能级处发生重叠,说明存在轨道杂化现象.并且Cu原子的电子基本分布在成键态,且在较低能级处与Ni的d轨道杂化.Cu原子掺杂后,使得Ni原子d轨道电子的PDOS尖峰变宽,也致使Ni7Cu模型的DOS在费米能级处的尖峰变宽.这说明Cu原子掺杂后,Cu原子的d轨道与邻近Ni原子的d轨道间发生d-d电子相互作用致使峰变宽,离域性变强.总之Cu原子掺杂进γ-Ni体系后,增加了Cu-Ni之间的相互作用,影响了原体系中电子的相互作用,导致各原子之间的键合强度也发生了变化.

图4 Ni8与Ni7Cu掺杂体系的总态密度和分波态密度图Fig.4 Partial and total electronic density of states of the systems with doping Cu in Ni8与Ni7Cu

2.4 差分电荷密度

为了更深层次地剖析Cu原子的掺杂使γ-Ni体系稳定性降低的原因,进一步研究Cu原子与周围Ni原子的键合作用,更直观地了解Cu原子掺杂前后体系中原子间的成键情况,选取Ni8与Ni7Cu掺杂晶胞的(001)面绘制差分电荷密度图,如图5所示.图5中蓝色表示电子缺失(减少),红色表示电子富集(增加).由图5可以看出掺杂导致原子的电子排布发生了明显的变化,从而引起差分电荷密度发生了变化.由图5a可以看出,未掺杂时,Ni原子与最近的Ni原子之间靠运动于它们之间的公有化的自由电子结合起来,表明Ni与Ni原子间的键合作用为金属键.Ni原子周围有电荷缺失,并且电荷缺失沿Ni-Ni(处在四个角上的Ni与处在中心的Ni原子)方向；从图5b可以看出,Ni8Cu掺杂晶胞(001)面中心的Ni原子被Cu原子取代后,Ni原子周围有电荷富集,并且电荷沿Ni-Cu方向富集,表明Ni-Ni、Ni-Cu之间共价键性增强.结合图4b可知Ni-Cu之间的化学键由Cu 3d和Ni 3d轨道的价电子杂化形成.

图5 Ni8及Ni7Cu掺杂晶胞(001)面差分电荷密度图Fig.5 Distribution of charge density difference of the systems in Ni8 and Ni7Cu along (001) plane

3 结论

1) 第一性原理计算表明,Cu原子的掺杂使γ-Ni体系的形成热、结合能的绝对值均降低,并且随着掺杂浓度的增大,形成热和结合能的绝对值依次降低,表明体系稳定性依次降低；Cu原子的掺杂使γ-Ni体系的弹性常数、体模量B、剪切模量G以及杨氏模量E均不同程度的降低,G/B的值稍有升高,表明Cu的掺入降低了体系的硬度、抗变形能力以及原子间的定向键和结合能力,使体系的延性降低.

2) 态密度以及(001)面的差分电荷密度表明当Ni7Cu掺杂晶胞(001)面中心的Ni原子被Cu原子取代后,Ni原子周围有电荷富集,Ni原子与Cu原子之间有键合作用,是由Cu原子d轨道和Ni原子d轨道的价电子杂化形成的.

3) Cu的加入促进了铸态Inconel 718合金中Laves相的析出,并且Cu的加入使合金的硬度和屈服强度均降低.实验结果与第一性原理计算结果的趋势相一致.

致谢：本文得到省部共建有色金属先进加工与再利用国家重点实验室开放基金(SKLAB02019014)项目的资助，在此表示感谢.