基于双脉冲特征的滚动轴承缺陷尺寸估计方法

剡昌锋,赵伟坤,孟佳东,2,王文斌,吴黎晓

(1. 兰州理工大学 机电工程学院,甘肃 兰州 730050; 2. 兰州交通大学 铁道技术学院,甘肃 兰州 730030; 3. 甘肃路桥新锐交通科技有限责任公司,甘肃 兰州 730100)

滚动轴承是旋转机械的核心部件，其工作状态直接影响整个机械系统的性能与安全，因此开展滚动轴承故障诊断研究可以有效避免生产过程中重大事故的发生[1].然而受现场环境的影响，设备早期故障的信号特征通常被噪声淹没，很难准确地识别[2].因此通过信号处理技术提取故障信号特征，估计缺陷尺寸大小和严重程度，为滚动轴承状态监测和剩余寿命的预测提供方法，具有广泛的应用前景和重要的研究价值.

Dowling[3]认为当滚动体通过内圈或外圈局部缺陷表面时，会在进入和退出缺陷的边缘分别产生一次冲击.Epps[4]在实验中发现：滚动体进入缺陷时产生主要包含低频成分的阶跃响应，而退出缺陷时产生包含高频成分的脉冲响应.Sawalhi等[5]提出了多体动力学模型研究缺陷轴承振动响应，在仿真结果和实验中都观察到了双脉冲现象.

近年来国内外学者在降低背景噪声、准确提取双脉冲特征和滚动轴承缺陷尺寸估计方面开展了研究工作.Zhao等[6]提出了单位白噪声的IMF-ApEn分布方法，用来提取有效IMF分量，从而实现阶跃成分与冲击成分的分离.孔佑炳等[7]采用EEMD对预白化处理后的信号进行降噪，利用Hilbert包络算法，分离出了剥落故障混合陶瓷球轴承振动信号中包含的双脉冲特征.Jena等[8]采用未定小波变换对振动信号降噪，基于symlet小波变换，得到滚动体经过缺陷的持续时间，进而估计缺陷尺寸大小.Khanam等[9]利用sym5小波基，对振动信号进行小波变换，从而得到滚动体进入和退出缺陷引起的振动响应.孙守保等[10]通过AR(Autoregressive)和MED滤波增强了故障特征信号，并用复Morlet小波提取最优频带特征信号，对所提取的特征信号进行包络并相加得到双脉冲特征.针对轴承缺陷尺寸估计问题， Sawalhi和Randall[11]给出了双脉冲信号特征与缺陷尺寸之间的关系，研究了轴承转速对脉冲间隔的影响.Moazen等[12]分析了振动特征与轴位移信号之间的关系，研究了滚动体经过缺陷时的漂移现象对缺陷尺寸估计的影响.Moazen等[13]的研究还表明滚动体进入点并非阶跃响应的最大值点，利用阶跃响应中最大值点和脉冲响应最大值点之间的间隔时间，估计缺陷尺寸会产生一定的误差.

针对多分量信号分离的时频分析方法的不足，Dragomiretskiy 等[14]提出了变分模态分解(Variational Mode Decomposition,VMD)方法.Jiang等[15]根据振动信号VMD分解后分量的峭度值最大原则，挑选其中包含冲击成分的IMF分量，通过多分辨率Teager能量算子(MTEO)解调判断轴承故障类型.张伟等[16]提出VMD和奇异值能量差分谱的滚动轴承故障特征提取的方法.

为了能从低信噪比的复杂振动信号中提取滚动体经过缺陷产生的双脉冲特征，本文提出了一种基于双脉冲特征的滚动轴承缺陷尺寸估计方法.采用AR预白化处理和VMD分解方法，以互信息和峭度值最大分别提取振动信号中包含阶跃成分和冲击成分的分量，通过平方包络增强阶跃与冲击成分，根据阶跃、脉冲特征与滚动体经过缺陷边缘的时间间隔关系，估计轴承故障缺陷尺寸，为轴承的状态监测和寿命预测提供了一种新的方法.

1 基于VMD提取双脉冲特征的方法

1.1 双脉冲信号特征提取

由于轴承外圈有故障时滚动体进入和退出缺陷时产生双脉冲现象，因此本文采用信号分离方法，得到滚动体进入缺陷时产生的阶跃信号和退出缺陷时产生的脉冲信号，用于识别故障缺陷尺寸.其算法流程如图1所示，主要步骤如下：

1) 对采集到的故障轴承振动信号通过AR预白化处理得到残差信号，去除了信号中的确定性成分，提高信噪比.

2) 采用VMD方法分解降噪后的振动信号，得到各分量信号.峭度指标对冲击成分敏感，因此以峭度最大的分量作为冲击特征分量信号.由于互信息反映两个变量之间的相关性以及共享信息量，所以在峭度值接近的情况下，以互信息最大的分量作为阶跃特征分量信号.

3) 将提取的分量信号分别进行平方包络，得到包络信号以及与滚动体运动实际情况相符的双脉冲特征，并确定双脉冲对应的时间间隔.

4) 根据轴承外圈缺陷的中心角θd与缺陷尺寸dl之间的几何关系，估计出轴承外圈的缺陷尺寸.

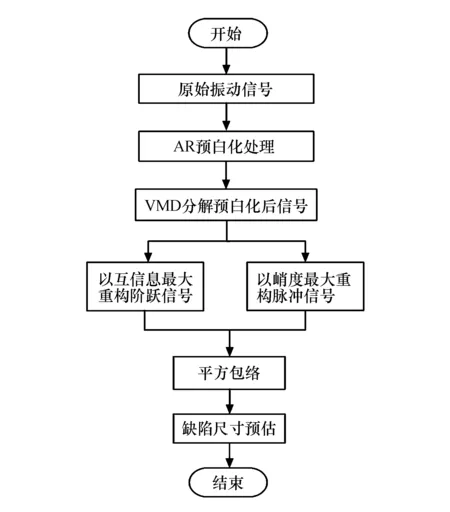
图1 技术路线流程Fig.1 The flowchart of technical route

1.2 变分模态分解

变分模态分解假设每个本征模态函数是具有不同中心频率的有限带宽，为使每个本征模态函数的估计带宽之和最小，通过转换解决变分问题，将各本征模态函数解调到相应的基频带，最终提取各个本征模态函数及相应的中心频率.

通过VMD方法将信号自适应地分解为有限个模态分量函数(IMF)，其表达式为

uk(t)=Ak(t)cos(φk(t))

(1)

式中：uk(t)表示幅值为Ak(t)的谐波信号;φk(t)表示谐波信号瞬时频率的积分.

假设f(t)为待分解的多分量信号，在进行K阶分解时，可以将其看作如下分解过程：

(2)

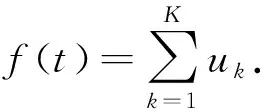
为得到式(2)的最优解，需将待求解约束变分模型变为非约束变分问题，通过引入增广Lagrange函数表达式计算式(2)约束变分的最优解，即

(3)

式中：λ为Lagrange算子;α为惩罚参数.

利用交替方向算子方法求取上述增广Lagrange函数的鞍点，即为式(3)的最优解，最终可以将原始信号分解为K个固定带宽的IMF分量.具体的实现过程如下：

(2) 开始执行循环n=n+1；

(3) 从内层开始执行第一个循环，根据式(4)更新uk：

(4)

(4) 令k=k+1，重复第(3)步，直到k=K，结束第一个内循环；

(5) 开始执行第二个循环，根据式(5)更新ωk：

(5)

(6) 令k=k+1，重复第(5)步，直到k=K，结束第二个内循环；

(7) 根据式(6)更新λ：

(6)

(8) 重复第(2)～(7)步，直到满足以下迭代条件，整个循环结束，最终输出结果，获得K个固定带宽的IMF分量：

(7)

2 轴承缺陷尺寸估计

当滚动轴承外圈出现故障时，缺陷尺寸dl与滚动体运行轨迹之间的几何关系以及典型的双脉冲特征如图2所示.从图2a可以看出:当某一个滚动体开始进入缺陷时，在A点应力卸载过程开始，随后达到局部最大D点;当该滚动体应力完全卸载产生阶跃响应，幅值增加并在B点达到峰值;之后轴承的滚动体滚过缺陷时，在C点撞击退出边缘并产生高频脉冲响应.根据图2b几何关系可以看出:O是轴承的中心，进入点在线OP上;由于接触变形，在滚动体与内、外圈之间存在两个椭圆接触区域;当接触变形区域到达进入边缘P点时，滚动体中心在A点，滚动体与外圈之间的椭圆接触面积的半长轴为a1;滚动体在B处进入缺陷中，此时滚动体与滚道之间的变形完全恢复，从进入边缘P点到滚动体中心B点之间的距离与滚动体的半径r相等.C点是滚动体与退出边缘Q点碰撞时的球心位置.A和B相对于进入点的角度位置分别定义为θ1和θ2.从A到B的时间被定义为进入时间te，从B到C的时间被定义为退出时间tp.

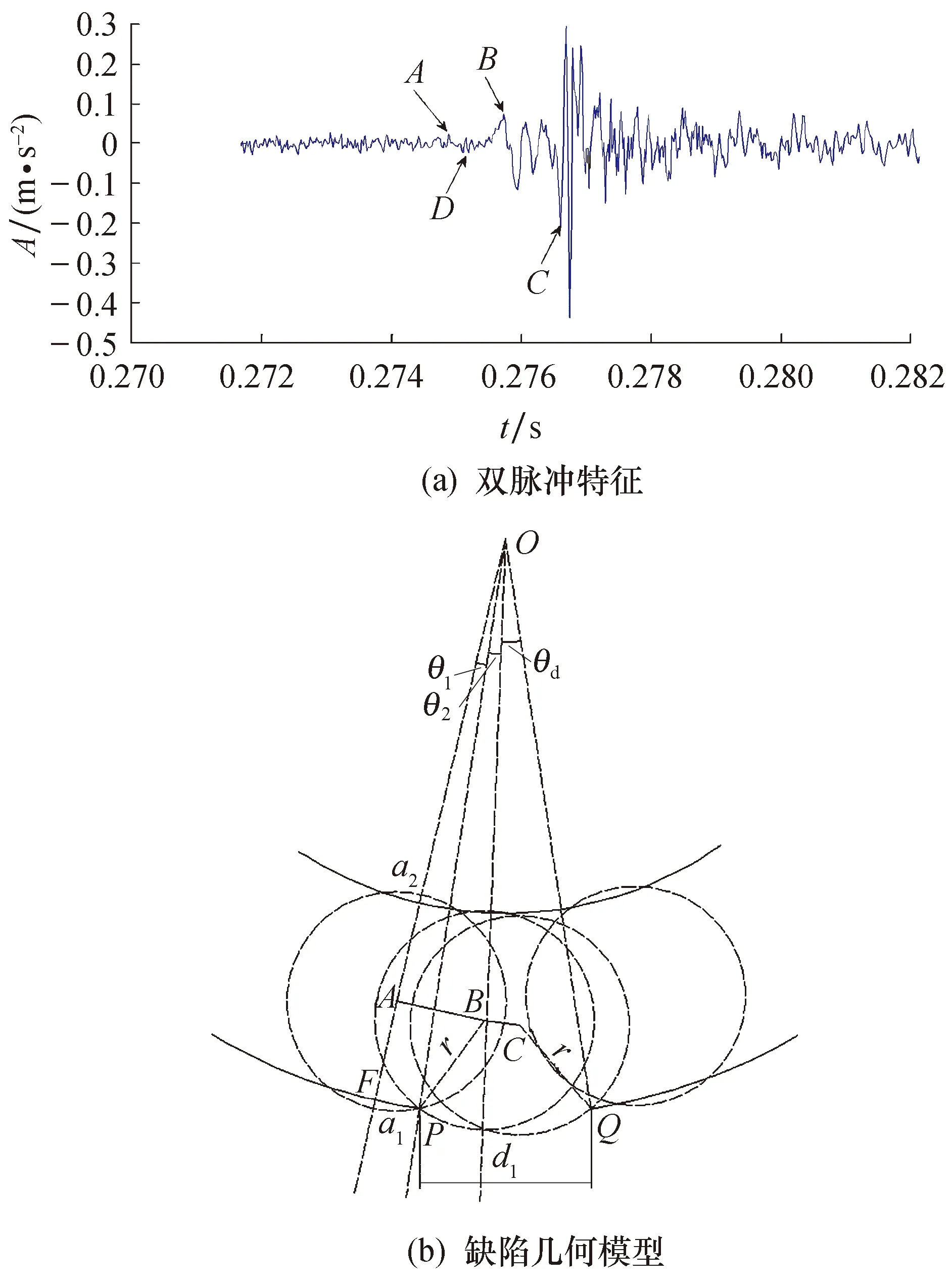
图2 双脉冲特征和缺陷模型

由赫兹接触理论得到滚动体与滚道之间的接触变形与载荷关系[17],可表示为

Q=Kδn

(8)

式中：Q为载荷；K为接触刚度；δ为接触总变形；n为接触载荷-变形系数，一般球轴承n=1.5.

根据赫兹接触理论，利用解析法可以求解出滚动体与内、外圈滚道之间的总接触变形量[17]：

δ=δi+δo

(9)

式中：δi、δo分别为滚动体与内、外圈之间的接触变形量.

由图2b几何关系可得:

式中：R为没有变形时滚动体中心到轴承中心的距离.

由于总变形量很小，θ1和θ2也非常小，假定滚动体为纯滚动，所以从A点到B点滚动体中心的速度恒定，则

(13)

式中：ωc为保持架转动角速度.

设转轴的角速度为ω，则ωc可表示为

(14)

式中：d、Dm分别为滚动体直径与轴承节圆直径.

θ1与θ2之间的比率可以定义为恒定值η，该值仅取决于轴承的几何变形量. 那么θ2和te之间的关系为

(15)

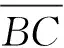
(16)

当滚动体与退出边缘Q点碰撞时，根据图2b的三角关系得到缺陷中心角θd：

(17)

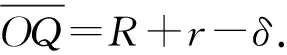
缺陷中心角θd可从振动信号中提取的te和tp计算得到.缺陷尺寸为

dl=2(R+r)sin(θd/2)

(18)

考虑滚动体滑动、轴承载荷和转速等的影响，会造成计算的θd有一定的误差.因此将产生的误差折合成误差系数β，对式(18)修正后的缺陷尺寸为

(19)

3 实验验证

本文采用美国凯斯西储大学(Western Reserve University)的故障轴承实验数据.试验台如图3所示，由一个2马力的电动机(左)，一个扭矩传感器/编码器(中)，测功机(右)和控制电子(未显示)组成.加速度计放置在电机外壳驱动端的六点钟位置对振动数据进行测量，采样频率为48 kHz，采样点数为20 000.试验用的测试轴承型号为SKF 6205-2RS 深沟球轴承，该轴承的几何参数见表1.用外圈故障数据作为测试数据，轴承的故障大小0.533 4 mm.

图3 凯斯西储大学试验台Fig.3 Test rig in Case Western Reserve university

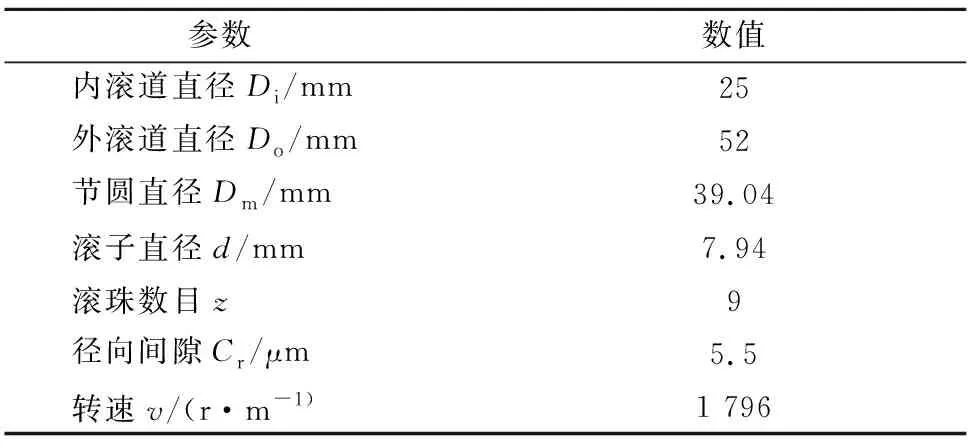
表1 SKF 6205-2RS深沟球轴承参数

3.1 双脉冲信号特征的提取

外圈故障原始数据对应的信号时域波形如图4所示.从图中可以看出,滚动轴承产生局部缺陷时滚动体经过缺陷处会产生固定周期且峰值较大的冲击成分.

图4 原始信号时域图Fig.4 Original signals in time domain

为了能观察到滚动体经过缺陷时引起的双脉冲特征，需对原始信号进行AR预白化处理[18].图5为AR预白化处理后的信号时域图，图6为预白化处理后的局部图.从图5和图6可以看出，原始信号经过预白化处理后消除了转频成分的影响，降低了背景噪声，提高了信噪比，因此有效平衡了振动信号中低频与高频之间的能量，滚动体引起的低频与高频成分都得到了增强.

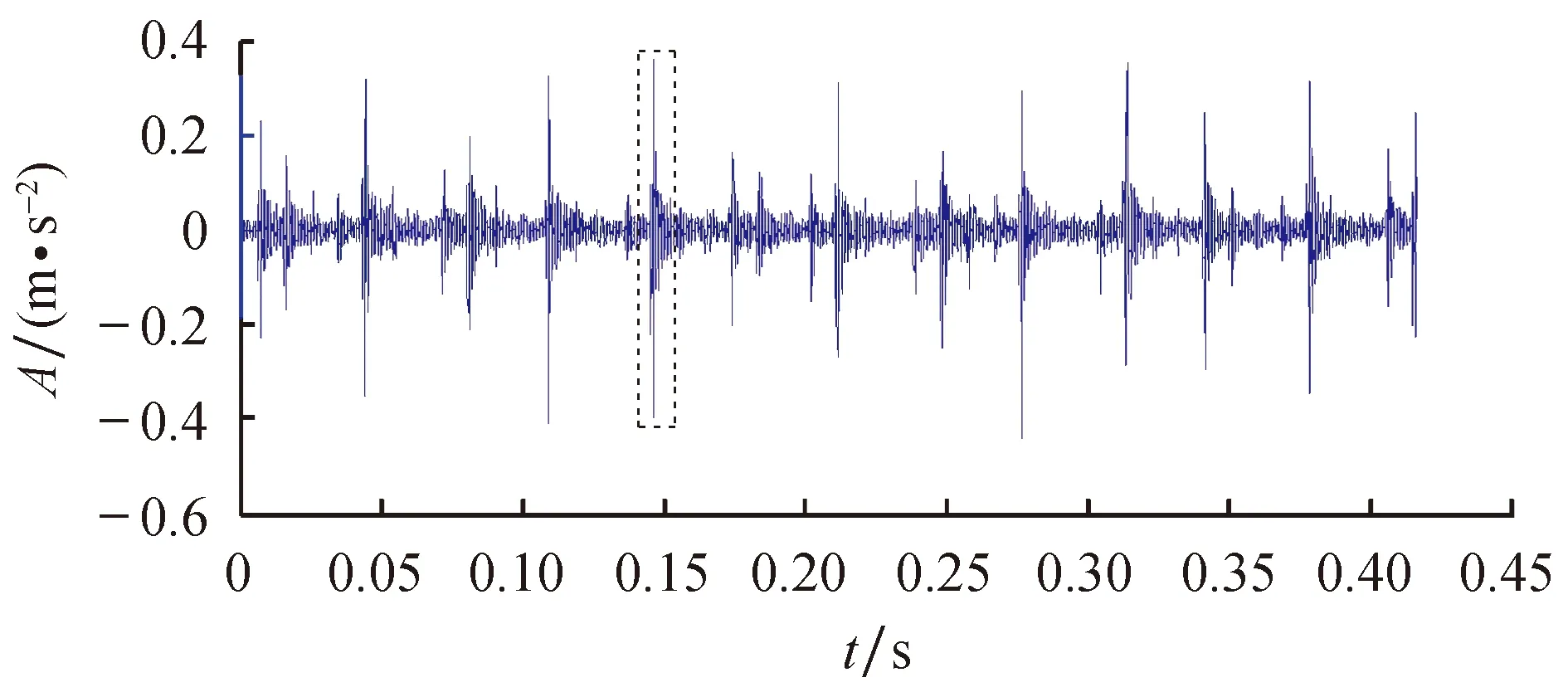
图5 预白化后的时域图Fig.5 Signals in time domain after pre-whitening

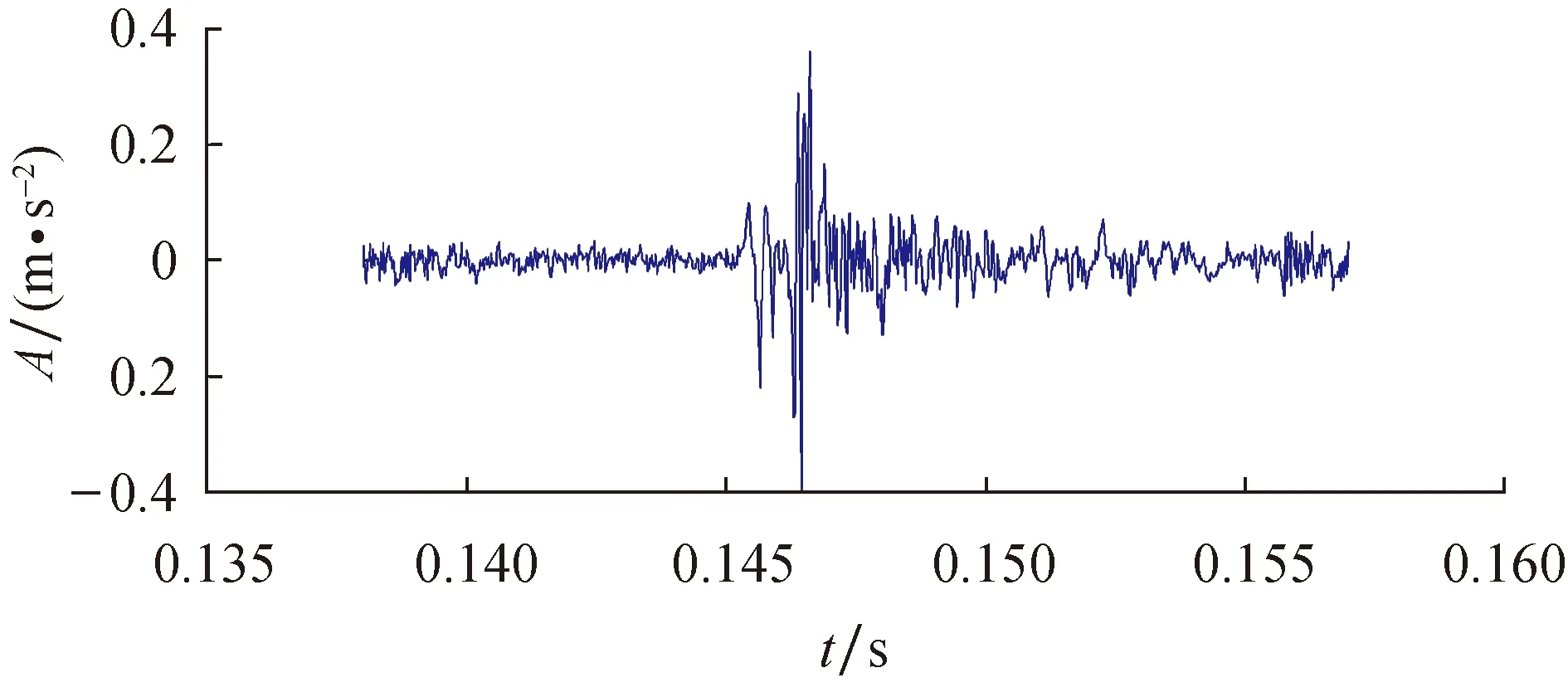
图6 预白化信号局部图Fig.6 Zooming signals after Pre-whitening

根据1.2节中变分模态分解的叙述，对预白化处理后的信号用VMD分解.设定VMD分量个数为7，得到分解后产生的7个模态分量时域波形如图7所示,经过计算得到7个分量的峭度和互信息值见表2.

表2 各VMD分量的峭度与互信息值

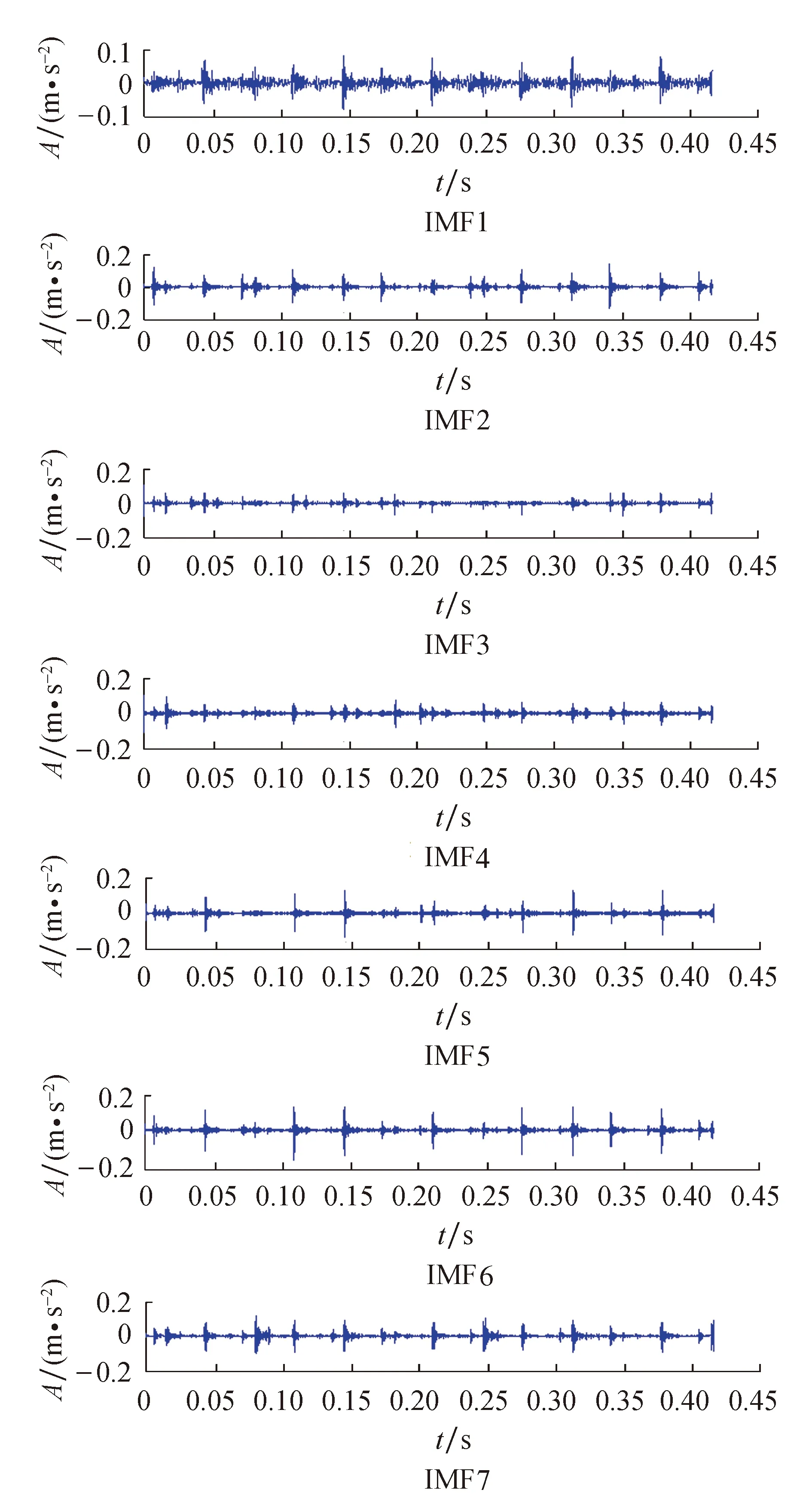
图7 信号VMD分解结果Fig.7 Decomposed signal components by VMD

从表2中可以看出IMF2和IMF7的峭度系数最大，将这两个分量进行重构作为冲击成分.在峭度接近的前提下，通过观察发现两个变量相互依赖程度的互信息中IMF1和IMF6最大，说明这两个分量与预白化处理后的信号有较强的关联性，用这两个分量重构的信号作为阶跃信号.

将通过筛选的有效分量信号分别进行重构，如图8所示，图8a表示阶跃成分，图8b表示脉冲响应成分，从图中可以看出重构后的冲击特征有效增强.通过图9局部放大图来看，阶跃成分并不能反应滚动体进入时刻信息，冲击成分中包含较宽的频带，因此对提取的信号进行平方包络，如图10所示.

图8 提取的双脉冲信号Fig.8 Extracted double pulse signals

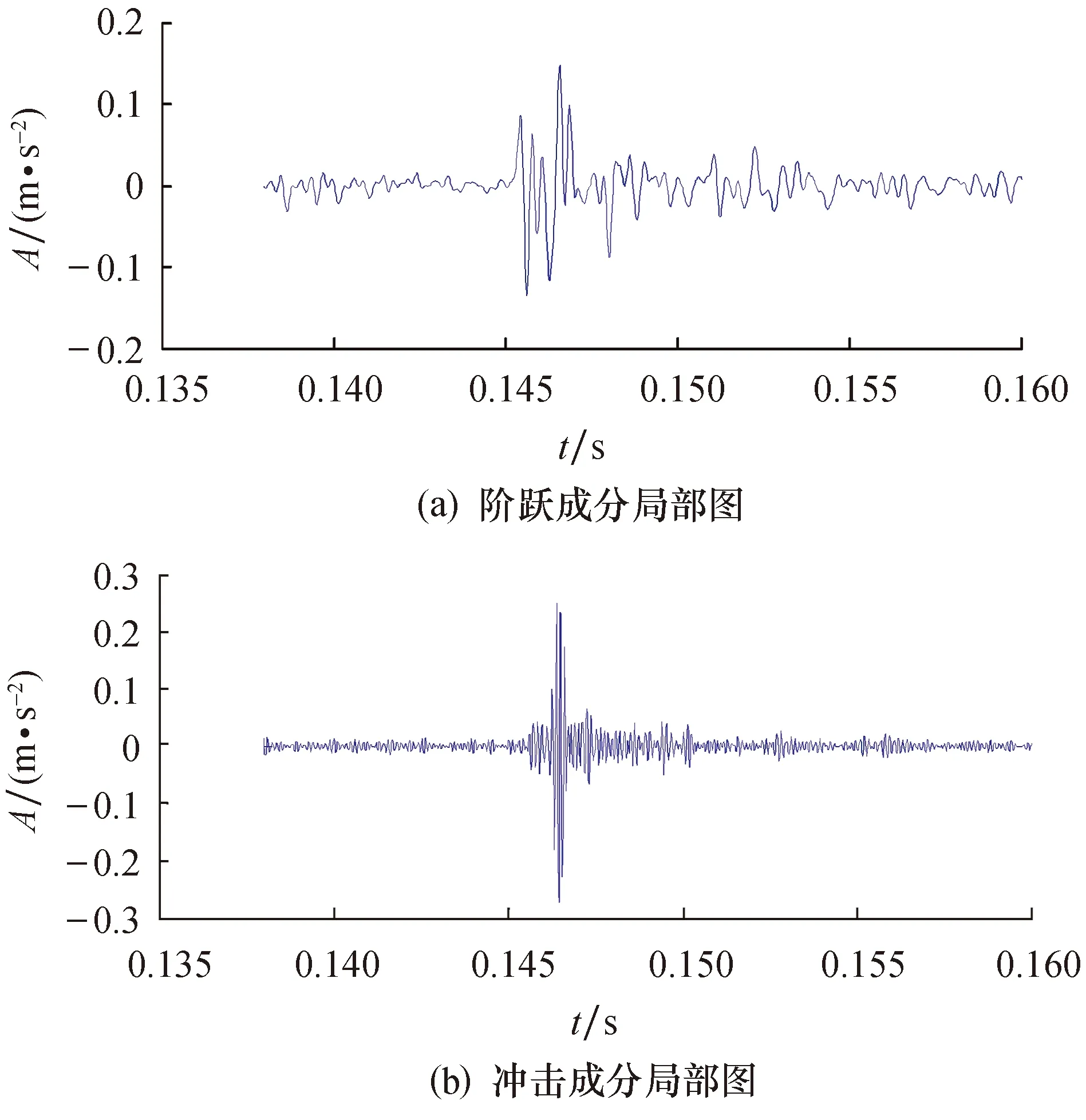
图9 提取的双脉冲局部放大图Fig.9 Zoomed in double pulse signals after extraction

图10 包络信号Fig.10 Enveloped signal

图10a和图10b分别表示阶跃和冲击成分的包络信号.从图10中可以看出信号的冲击成分和阶跃成分都得到增强.为了能够准确得到反映滚动体进入和退出的时刻信息，将得到的包络信号图进行局部放大如图10c和图10d所示.从图中可以看出， 本文提出的方法能够准确提取滚动体经过缺陷时产生的双脉冲特征.

3.2 故障缺陷尺寸计算

通过上述分析，根据第2节中的理论分析，图10c中阶跃成分包络起始点A与图2a中A点对应，可以看作滚动体进入缺陷时的进入点，得到进入时间te.滚动体退出缺陷时产生频带较宽的冲击成分，因此可以将图10d冲击成分包络的起始处C看作是滚动体撞击退出边缘的退出点，与图2a中的C点对应，得到退出时间tp.通过式(15～17)得到的时间间隔和中心角θd，带入到缺陷估计式(18)中，得到滚动轴承外圈故障缺陷尺寸为0.527 9 mm.与实验中轴承故障大小0.533 4 mm相比，误差为1.03%，结果基本一致.

4 讨论

4.1 不同转速对故障缺陷尺寸估计的影响

为了研究不同转速对缺陷尺寸估计的影响，验证本文所提方法的有效性，采用与3.1节中信号处理相同的步骤,对不同转速下外圈存在相同缺陷尺寸的滚动轴承故障信号进行分析，提取双脉冲特征.根据本文提出的缺陷尺寸计算方法对缺陷尺寸估计，将理论值与计算值进行对比，讨论转速对缺陷尺寸估计的影响.采用西储大学轴承实验数据，缺陷尺寸为0.533 4 mm，轴承的转速分别为171 9、1 747、1772r/min，图11～13为这几种转速下得到的双脉冲特征波形.

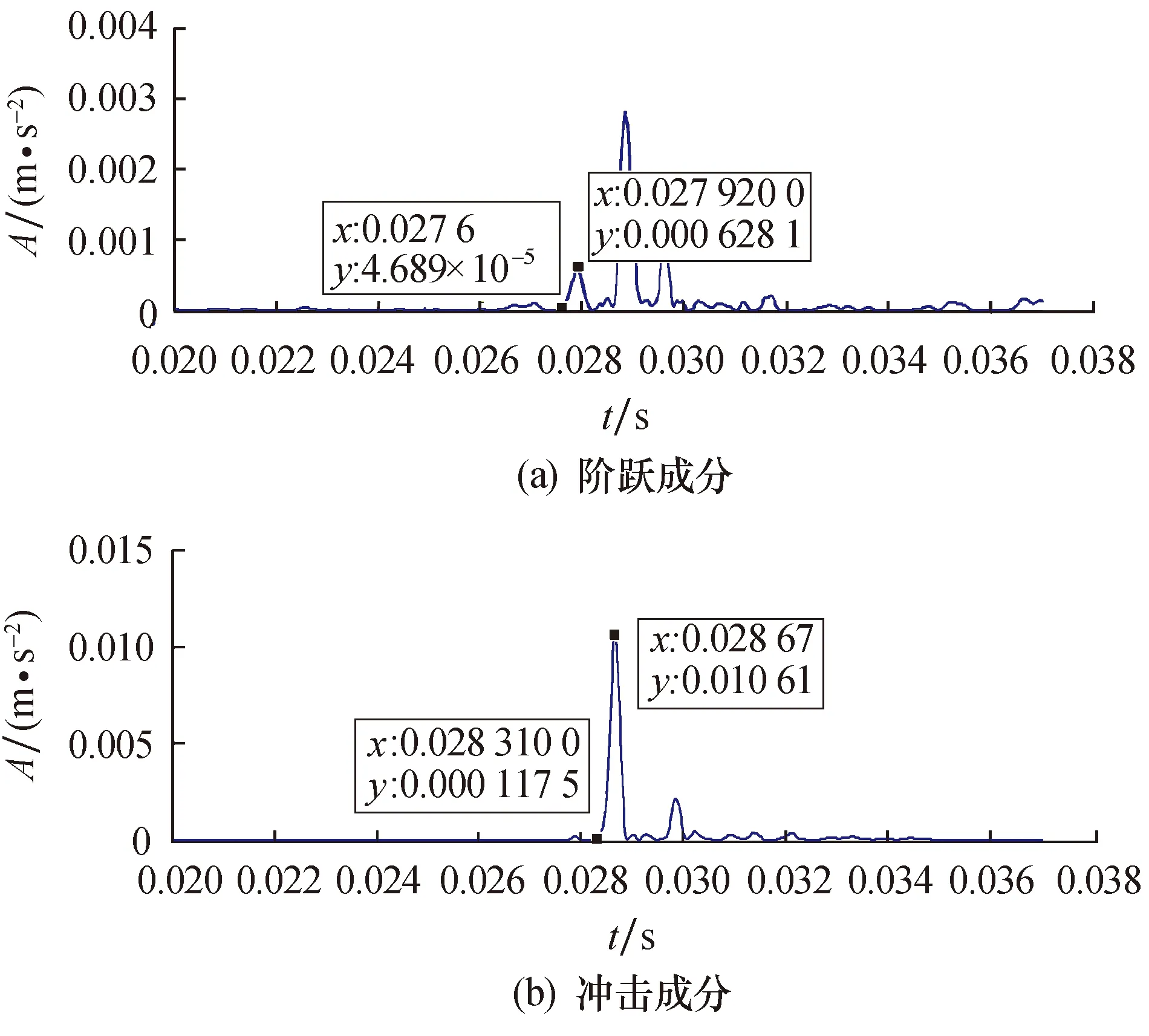
图11 转速为1 719 r/min提取的双脉冲信号Fig.11 Double pulse signals extracted at 1 719 r/min

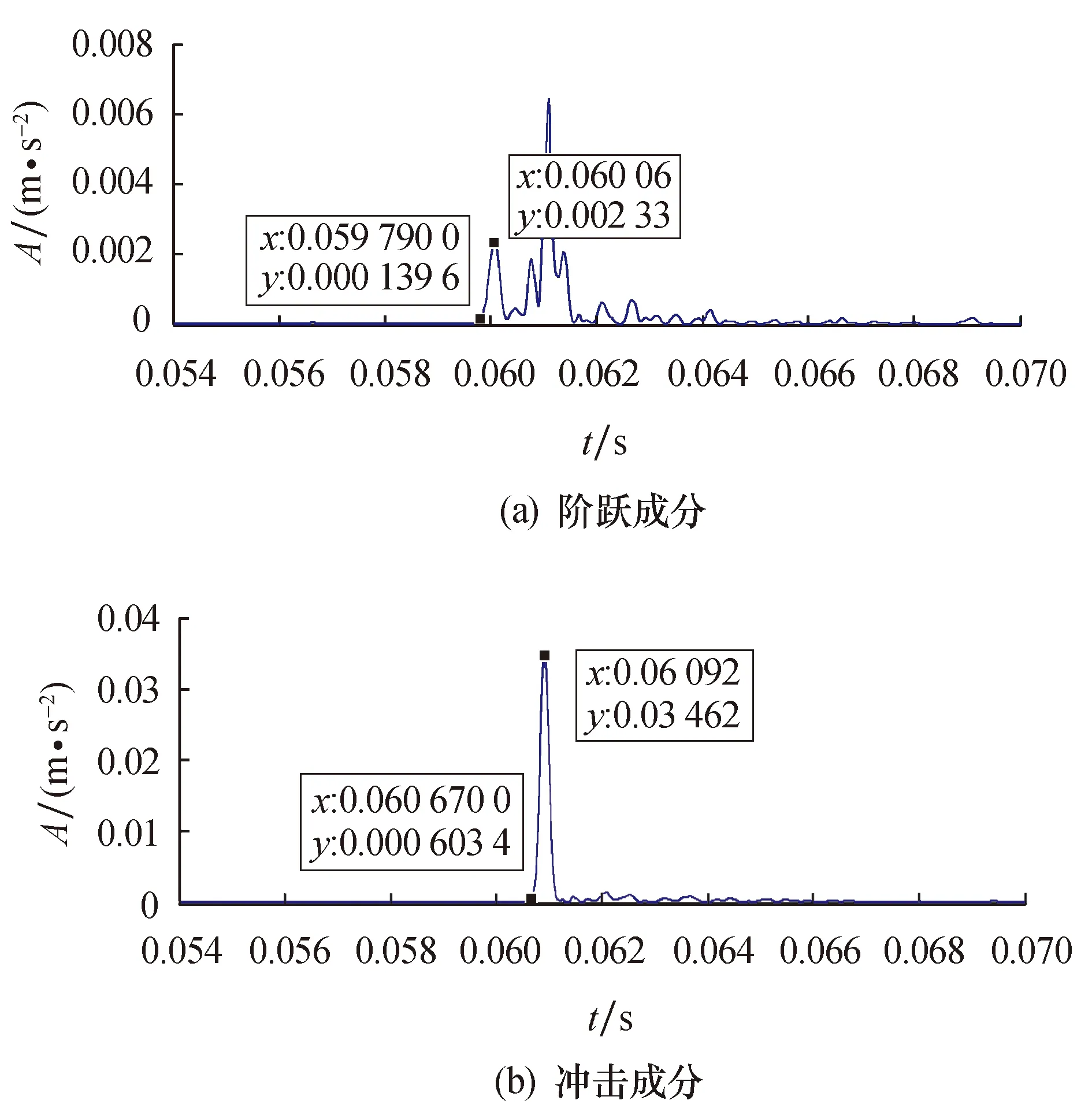
图12 转速为1 747 r/min提取的双脉冲信号

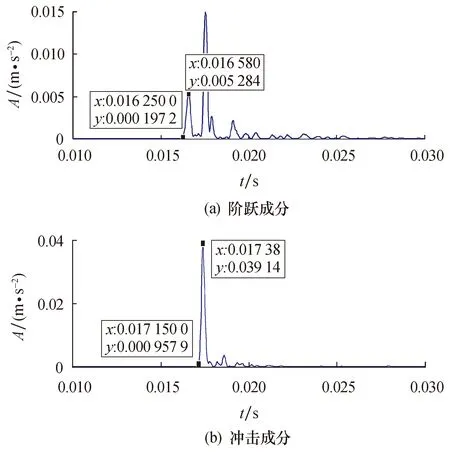
图13 转速为1 772 r/min提取的双脉冲信号Fig.13 Double pulse signals extracted at 1 772 r/min

在不同转速下，提取得到双脉冲特征对应的时间间隔，并依次带入缺陷尺寸计算式(18)，得到对应的转速与估计缺陷尺寸之间的关系如图14所示.

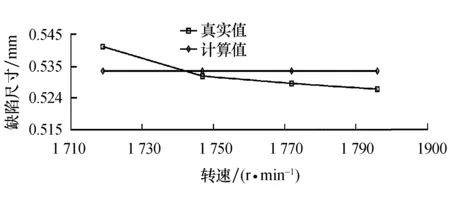
图14 不同转速下缺陷尺寸估计值Fig.14 Estimated defect size at different shaft speeds

从图14可以看出，在缺陷尺寸相同而转速不同时，根据双脉冲特征信号估计得到的缺陷尺寸与真实值结果基本一致.转速从1 719 r/min到1 796 r/min提高时对应的缺陷尺寸会有微弱的下降趋势，即转速对缺陷尺寸的估计有一定的影响，但是影响并不是很大，从而进一步验证了本文方法的有效性和鲁棒性.

4.2 不同缺陷尺寸对故障缺陷尺寸估计的影响

研究不同缺陷尺寸对轴承振动响应和缺陷尺寸估计的影响，对于揭示轴承缺陷的演化规律有着重要的意义.对轴承转速为1 796 r/min、缺陷尺寸为0.177 8 mm和0.355 6 mm的故障轴承加速度信号进行研究，得到如图15和图16所示的双脉冲特征波形.

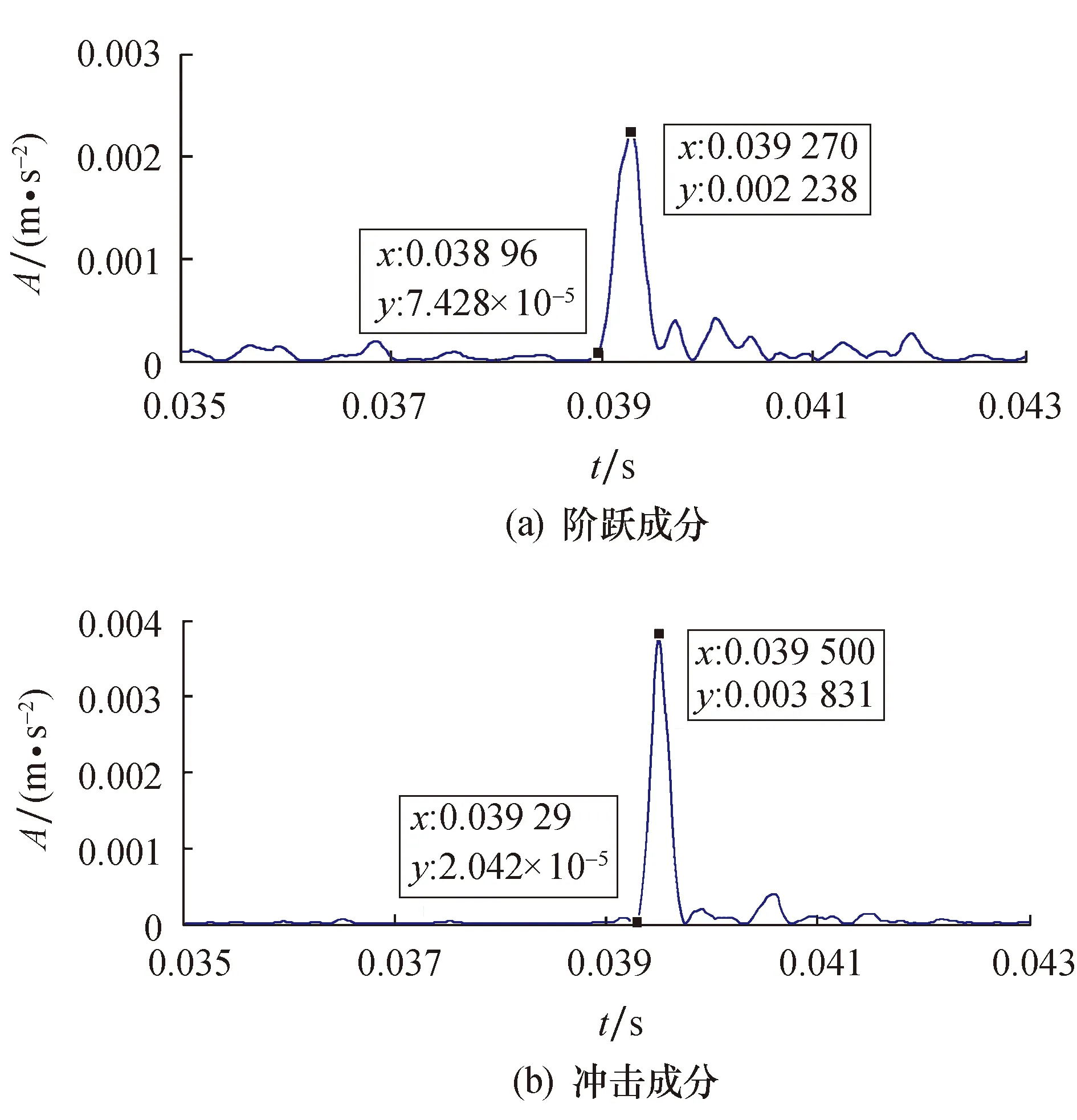
图15 在1796 r/min下提取的0.1778mm的双脉冲信号Fig.15 0.177 8 mm double pulse signals extracted at 1 796 r/min

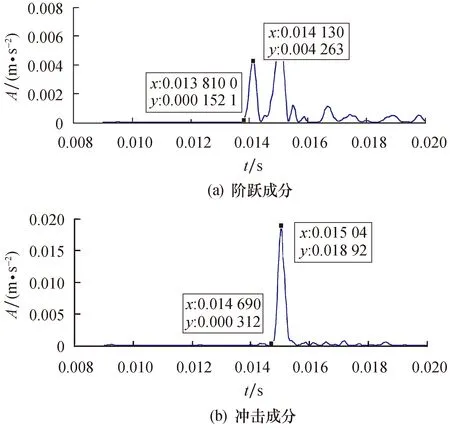
图16 在1 796 r/min下提取的0.355 6 mm的双脉冲信号Fig.16 0.355 6 mm double pulse signals extracted at 1 796 r/min

根据图15和图16的双脉冲特征，得到不同缺陷尺寸下的估计值如图17所示.从图17可以看出:缺陷尺寸较小时，估计的缺陷尺寸与实际值存在较大的误差；当缺陷尺寸较大时，本文提出的估计方法精度更高.

4.3 误差原因分析

虽然从上述分析结果中能够得到较为准确的缺陷尺寸，但是估计结果与真实值之间仍然存在一定的误差，主要的原因有以下几个方面：

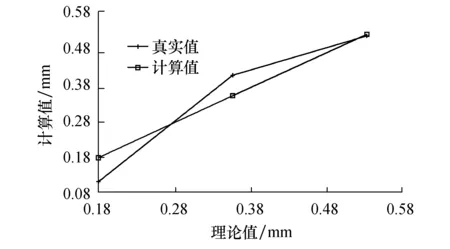
图17 不同理论缺陷尺寸下缺陷尺寸估计值Fig.17 Estimated values of defect size under different theoretical defect sizes

1) 本文缺陷尺寸估计模型中假定内圈圆心与外圈圆心重合，当对轴承内圈施加向下载荷时，由于滚动体与内、外圈滚道之间弹性变形的综合作用，使得内圈圆心向下产生一定的位移量，会影响中心角的测量.

2) 滚动体与保持架之间相互作用也会对滚动体经过缺陷时的速度产生一定的影响，从而影响ωc，使得计算结果产生一定的偏差.

3) 由于该试验验证中采用的滚动轴承缺陷尺寸较小，在缺陷尺寸估计模型中提取的时间会有一定的偏差，从而造成角度误差影响计算精度.如果滚动轴承有较明显的缺陷，其计算结果的误差会小.

4) 振动信号的采样频率会影响到式(18)的精度，在缺陷尺寸较小时，影响更加明显.

5) 由于振动传感器安装在外壳上而不是在轴承外圈上，传递路径会影响到提取的双脉冲特征准确度.

5 结论

1) 针对故障轴承滚动体经过缺陷时加速度信号产生的双脉冲现象，提出了一种基于双脉冲特征的滚动轴承缺陷尺寸估计方法.该方法将预白化处理后的信号经过VMD分解，通过峭度和互信息指标提取阶跃和冲击成分，从而确定滚动体进入和退出缺陷的时间间隔.根据所提出的缺陷尺寸模型，实现故障轴承缺陷尺寸的估计.

2) 通过实验验证了所提出的缺陷尺寸估计模型的正确性，研究不同转速和不同缺陷尺寸大小对其影响规律，并分析了所产生误差的原因.