双船浮托法中三船系统的水动力
李怀亮,李新超,张万里,阮志豪
(1.海洋石油工程股份有限公司,天津 300461;2.能威(天津)海洋工程技术有限公司,天津 300392)
0 引 言
在海洋资源被人们日益重视的今天,海洋工程领域开始大量地应用多浮体系统。区别于单浮体结构,多浮体系统是指由几个距离较近且必须考虑相互作用的海上结构物构成的整体。在工程应用领域中有大量的多浮体结构,比较具有代表性的有:浮式液化天然气生产储卸装置(LNG Floating Production Storage and Offloading Unit,FLNG)装卸系统、应用双船浮托法对油气平台上部结构物进行安装与拆除时的双驳船系统、浮式生产储卸油装置(Floating Production Storage and Offloading,FPSO)串靠或旁靠外输的双浮体系统、重大件运输中浮式货物与半潜船的双浮体系统、浮式起重机船与运输船小间隙并靠进行吊装作业时的双浮体系统、超大型海上浮式结构物(Very Large Floating Structure,VLFS)等。
在多浮体系统中,结构物之间的影响不可忽略,其受力和运动不像单浮体结构物一样简单。多浮体水动力干扰理论的研究针对的是结构物与其附近流体的运动以及流体对结构物的作用力,其基础原理是单浮体结构物的水动力原理,并在其中考虑多浮体系统的理论难点。较多学者对多浮体之间水动力的相互影响进行研究,并且在水动力干扰理论研究的基础上进行许多数值计算分析。SHIN等[1]应用三维势流方法对多浮体之间的相互作用进行研究。INOUE等[2]应用面元法计算FLNG系统的运动响应。CHAKRABARTI[3]应用多重散射与面元法相结合的方法计算不同浮体之间的相互作用。LEE等[4]应用面元法计算更为复杂的浮式结构物如海上移动基地(Mobile Offshore Base,MOB)的水动力。ALI等[5]采用面元法计算规则波中自由漂浮的多个直立圆柱式结构相互作用的水动力系数。吴广怀等[6]在多浮体系统中考虑浮体间距的影响。朱仁传等[7]基于三维势流方法,通过数值模拟分析结构物间距的影响,证明某些频率处出现强烈共振,但未能准确预报。
本研究的目标是在使用双船浮托法安装组块的过程中组块由运输船转移至2艘浮托船时的三船并靠系统,综合分析各船舶的水动力系数及相互影响机理,采用行业通用的水动力计算软件WAMIT重点分析运输船与两侧浮托船之间的距离对水动力系数的影响,以及当三船距离非常小时水动力系数的共振现象。
1 计算理论
根据势流理论,假定计算流场中为不可压缩、无黏、无旋的理想型流体,多浮体由无初始速度的N个单浮体组合而成,在多浮体中单浮体M的速度势φM为
(1)
式中:φI,M为施加在浮体M上的入射波速度势;φD,LM为因浮体L的存在而对浮体M产生影响的绕射势,也包含浮体M对自身作用形成的绕射势;φj为当浮体M位置不动时,由于其他单浮体运动,施加在浮体M上的辐射势,也包含浮体M对自身作用形成的辐射势;ξj为浮体自由度j的运动响应;ω为波浪圆频率;t为时间。
入射波速度势φI,M可表示为

exp[-i(kxcosβ+kysinβ)]
(2)
式中:g为重力加速度;A为波浪幅度;H为波高;k为波数,是色散关系ω2/g=ktanh(kH)的实根;h为水深;β为平面行进波与x轴之间的夹角。
在计算流域中,浮体的速度势φ满足Laplace方程
∇2φ=0
(3)
并满足统一自由面、平整海床、物面及远方辐射等边值条件[5],则边值问题可利用Green公式转化为物面上的积分方程求解:
(4)
(5)
式(4)和式(5)中:n为垂直作用在物体表面并指向流场的单位向量;φI(xi)为入射势;φD(xi)为绕射势;Si为第i个单元的面积。
浮体在频域下的运动方程为
(6)
式中:Mij、Cij、Fi分别为第i个单浮体的质量矩阵、静复原力矩阵、激励力矩阵;Aij和Bij分别为附加质量矩阵和阻尼矩阵。
2 算 例
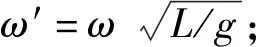

图1 圆柱形与长方形浮体

图2 圆柱形与长方形浮体相互作用水动力系数对比
根据计算结果与参考文献的对比,本计算方法及其结果与参考文献基本吻合。
3 三船系统
3.1 双船浮托法
浮托安装技术近年来在国内外取得不断的发展,与传统吊装方式相比,浮托法解决了超大、超重组块的海上安装难题,有效简化采用传统分块吊装再安装的复杂作业程序并缩短海上各设备连接调试时间。随着超大型及重型平台上部组块的出现,单船浮托法会受到相应驳船浮托能力的限制,同时对于一些下部结构没有设置开口的浮式结构,如张力腿平台(Tension Leg Platform,TLP)、Spar平台等,单船浮托法无法进行上部组块的浮托安装,由此需采用双船浮托法进行组块安装。
组块由运输船转移至2艘浮托船(简称过驳,见图3)是应用双船浮托法安装组块的关键步骤。在过驳过程中,运输船与2艘浮托船相距较近,不能忽略其相互影响。

图3 过驳示例
3.2 船舶模型
为分析过驳过程中运输船与2艘浮托船之间的间距对三浮体系统水动力性能产生的影响,考虑简化比较过程,选取3艘姐妹船作为运输船和2艘浮托船。船舶主要参数如表1所示。

表1 运输船及浮托船主要参数
图4为运输船和浮托船的水动力模型,以及坐标系和浪向定义,运输船与2艘浮托船的净距均为d,考虑作业海域为渤海,取水深h=10 m。

单位:m图4 船舶湿表面模型及坐标系和浪向定义
4 水动力分析
4.1 浮体间距影响

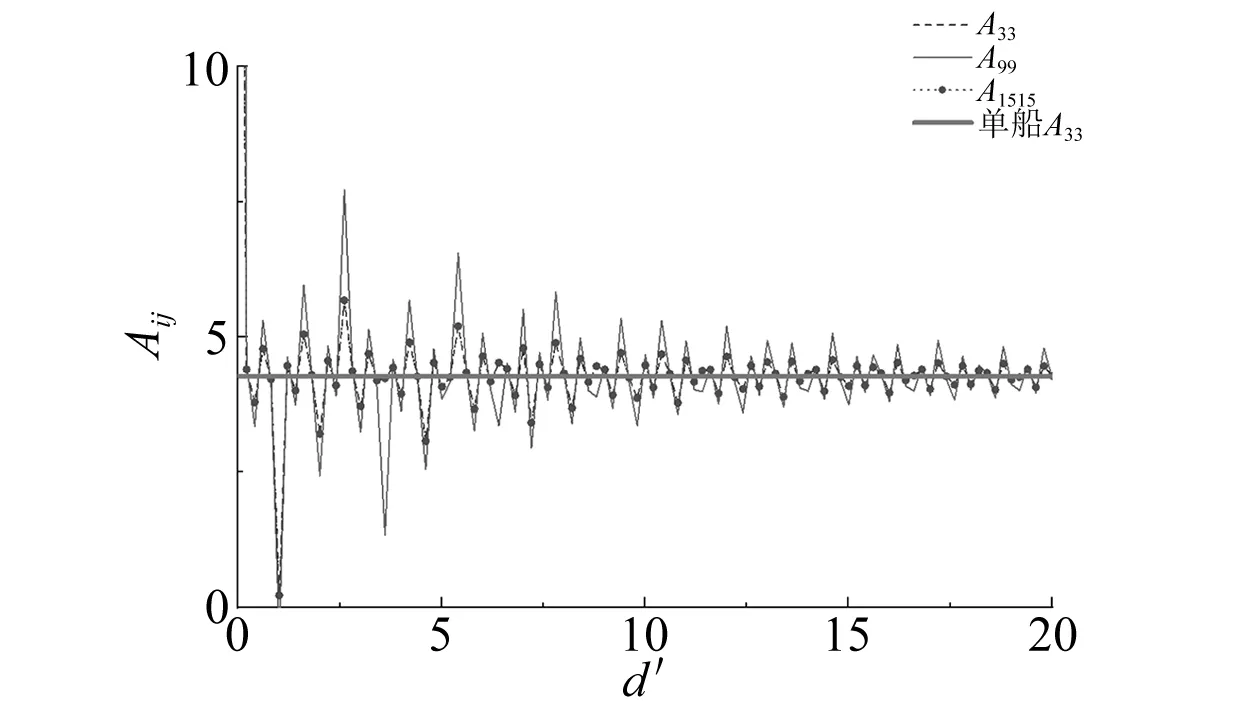
图5 浮体自身垂荡附加质量系数与浮体间距关系

图6 浮体相互作用垂荡附加质量系数与浮体间距关系

图7 浮体自身垂荡阻尼系数与浮体间距关系
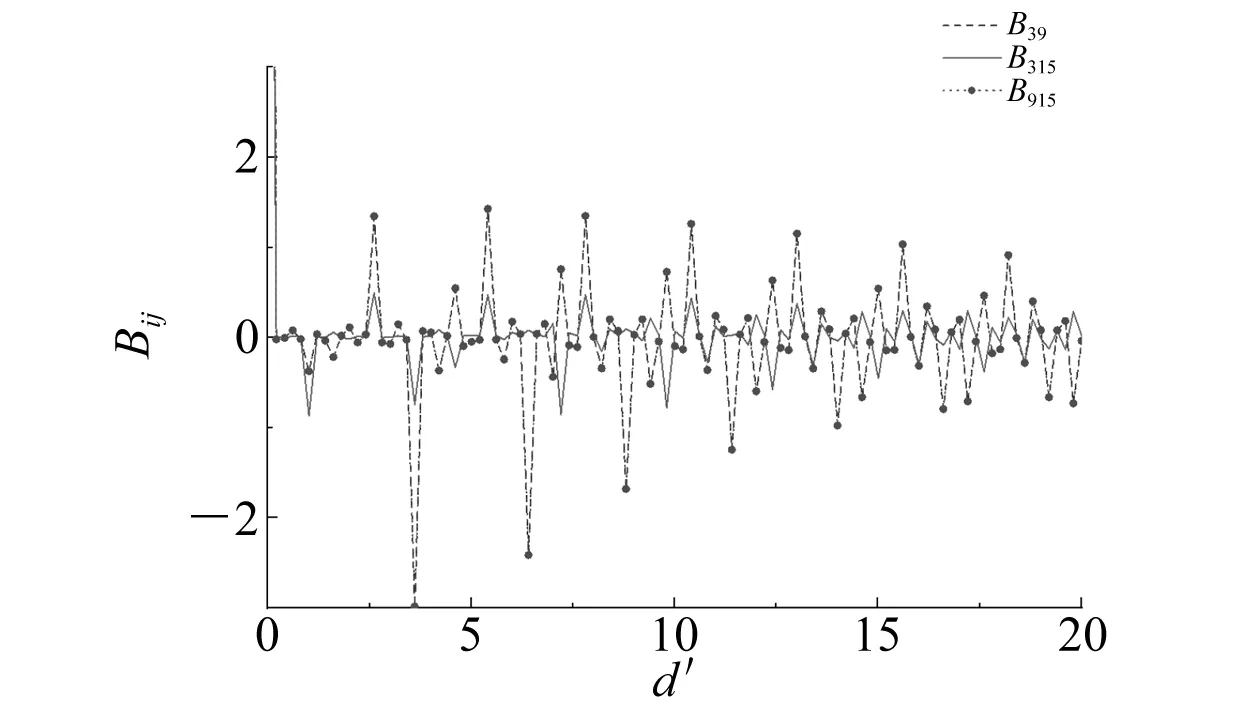
图8 浮体相互作用垂荡阻尼系数与浮体间距关系
由图5~图8可知,对于三驳船系统,由于运输船与两侧浮托船之间的距离变化:船舶自身水动力系数(A33、B33、A99、B99、A1515、B1515)在单船时的水动力系数附近振荡,且随着运输船与两侧浮托船之间距离的增大,振荡幅值逐渐减小;运输船自身水动力系数(A99、B99)振荡幅值大于2艘浮托船自身水动力系数(A33、B33、A1515、B1515)的振荡幅值;2艘浮托船自身水动力系数(A33与A1515、B33与B1515)完全相同;船舶自身水动力系数振荡曲线相邻极大值或极小值之间的距离约为半个波长;三船间相互作用的水动力系数(A39、B39、A315、B315、A915、B915)在0附近振荡,且随着运输船与两侧浮托船之间距离的增大,其振荡幅值逐渐减小;当间距较大时,运输船与2艘浮托船相互作用的水动力系数(A39、B39、A915、B915)的振荡幅值大于2艘浮托船相互作用的水动力系数(A315、B315)的振荡幅值;2艘浮托船与运输船相互作用的水动力系数(A39与A915、B39与B915)完全相同;2艘浮托船与运输船相互作用的水动力系数振荡曲线相邻极大值或极小值之间相距约1个波长;2艘浮托船相互作用的水动力系数振荡曲线相邻极大值或极小值之间的距离约为半个波长;在运输船与两侧浮托船间距较小时,船舶自身的水动力系数及船舶相互作用的水动力系数均发生突变。
4.2 小间距共振
根据第4.1节,当运输船与两侧浮托船间距较小时,船舶自身的水动力系数及船舶相互作用的水动力系数均发生突变,而在双船浮托过驳工况下,运输船与两侧浮托船之间的间距通常较小,因此有必要对小间距下的情况进行深入研究。


图9 小间距并靠时三浮体附加质量系数

图10 小间距并靠时三浮体阻尼质量系数
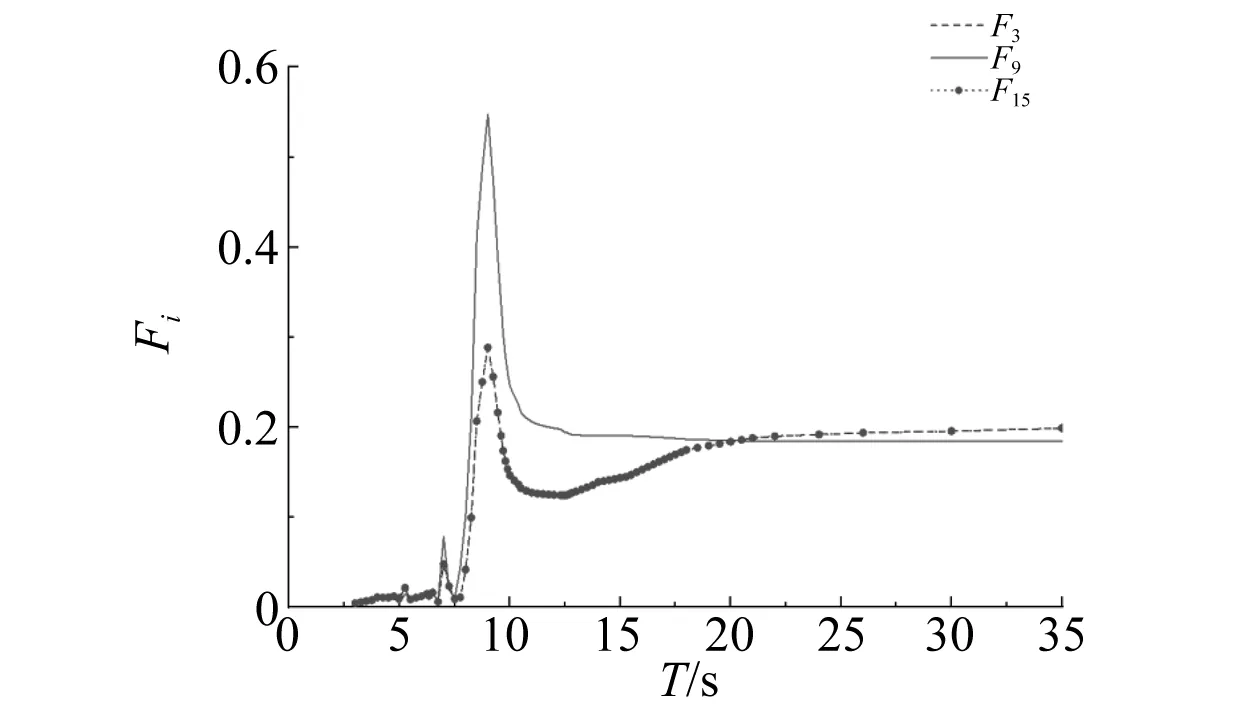
图11 小间距并靠时三浮体180°波浪力
由图9~图12可知,当运输船与两侧浮托船间距较小时,船舶的水动力系数和波浪力均在特定的波周期发生共振现象,且运输船的共振幅值明显高于两侧浮托船的共振幅值。由图12可知,就波浪力而言,被遮蔽船舶(运输船和浮托船B)所受到的波浪力在大部分波周期明显小于迎浪侧船舶(浮托船A)所受到的波浪力。

图12 小间距并靠时三浮体90°波浪力
如图13所示,当船舶的长度发生变化时(保持宽度和间距不变),船舶水动力系数和波浪力共振的波周期也会相应地发生变化。通过对一系列水动力系数和波浪力的计算发现,受浮体小间距影响,船舶水动力系数和波浪力均会在特定的波周期发生共振现象,共振发生的波周期对应的波长Lw基本介于0.5~1.0倍船长之间。
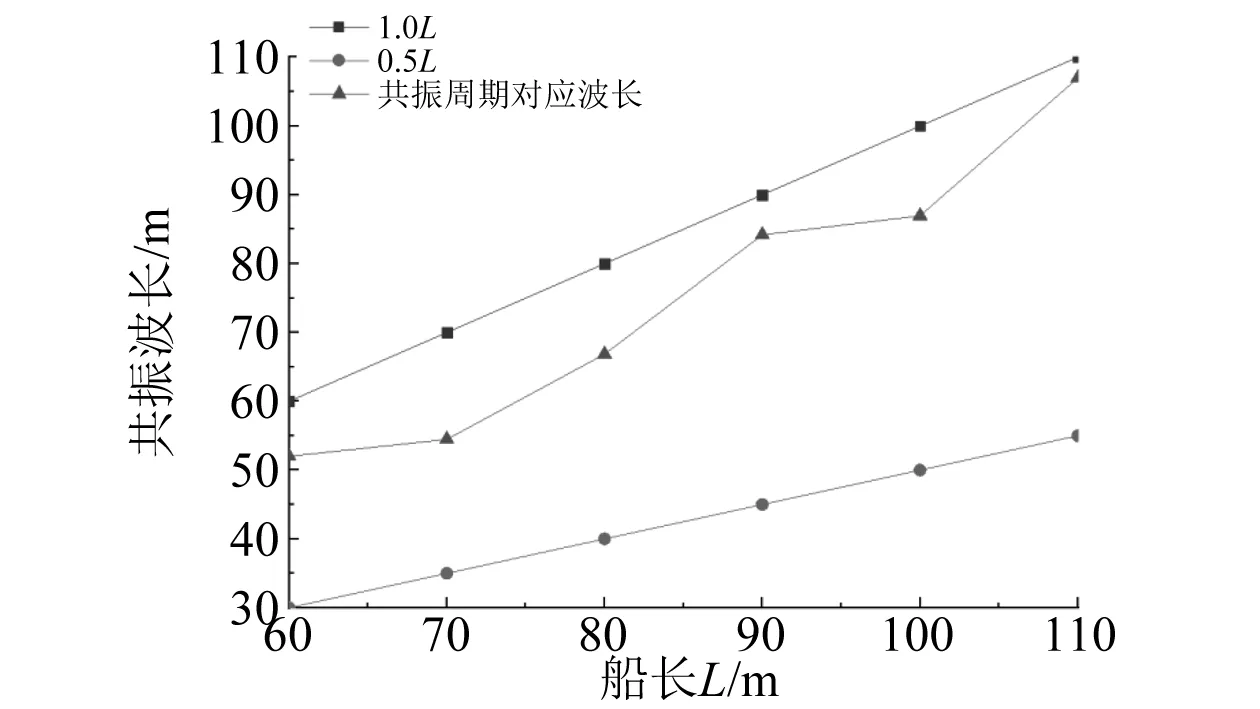
图13 小间距时发生共振的波长与船长关系
5 结 论
(1) 在双船浮托过程中,船舶间相互作用的水动力系数和船舶自身的水动力系数可达到同一数量级,因此对于双船浮托这种多浮体系统,必须考虑船舶间水动力相互作用的影响。
(2) 由于多浮体之间具有相互影响,水动力系数在某个定值附近振荡,当浮体之间距离增加时,水动力系数的变化幅度逐渐变小并收敛至定值,但是收敛速度较慢。
(3) 水动力系数极值点的出现有一定的规律,船舶自身及两侧浮托船相互作用的附加质量和阻尼相邻极值(极大或极小)之间的距离约为半个波长,2艘浮托船与运输船相互作用的附加质量和阻尼的相邻极值(极大或极小)之间的距离约为1个波长。
(4) 当运输船与两侧浮托船间距非常小时,船舶的水动力系数及所受的波浪力会出现共振现象,共振发生的波周期对应的波长基本介于0.5~1.0倍船长之间。
基于WAMIT,采用数值模拟方法对双船浮托过驳过程中三船并靠系统的水动力进行研究,根据研究结果,在设计双船浮托方案时,需考虑船舶间水动力的相互影响,应综合船舶能力、尺度、波周期、波长、船舶间距等因素,同时由于小间距、多浮体系统的水动力相互影响的复杂性,建议在进行双船浮托方案设计时开展进一步的物理水池试验。

