复合地基离心模型试验变形测试
姜彦彬,何宁,周彦章,朱锐,蔡忍,石北啸
(1.金陵科技学院 建筑工程学院,江苏 南京 211169;2.南京水利科学研究院 岩土工程研究所,江苏 南京 210029)
土工离心模型试验借助离心机的高速旋转为模型创造一个与原型应力水平相同的应力场,从而使原型的性状在模型中再现,是以自重为主要荷载的岩土工程技术研究中最先进、最有效的手段之一,并广泛应用于岩土工程工作机理、设计参数、方案比选和论证以及计算方法验证等方面的研究[1]。
变形测量是土工离心模型试验中最基础、最重要的测试内容之一,用于分析地基沉降、边坡稳定等岩土工程问题。点测量和面测量是模型变形测量中最为常见的2种方法[2]。点测量法可使用差动式位移计、激光测距仪等测量模型某点的位移,其精度高、连续性好,但受空间限制而只能布置有限数量的测点;面测量方法通常采用图像处理技术跟踪模型中预先布设的标点或土体自身特征点以获得模型平面位移场,包括粒子图像测速法(particle image velocimetry,PIV)[3],三步搜索算法等图像分析方法[4],所测位移场密集,但标点误差和图像处理手段对其精度影响较大。人工测量标点法精度低且无法在高重力场中进行,而作为一种补充测量手段在文献[5]中仍在沿用。
路堤下刚性桩复合地基(又称桩承式路堤)通过土拱效应将路堤荷载向桩顶集中并传递至压缩性更小的深层地基,具有总沉降小、稳定性好、工期短等优点,在土性差、工后沉降要求高的软基处理工程中得到了广泛的重视和应用[6]。变形控制是桩承式路堤设计的重要环节,涉及施工期变形稳定及工后沉降控制。离心模型试验已成为研究复合地基变形及承载特性的重要手段,路堤荷载下的复合地基离心模型试验变形测试内容包括离心机加、减速过程引起的加、卸荷变形,长期堆载排水形变及边坡附近侧向位移等变形测试内容,涉及土工离心模型试验变形测试的重要基本手段与研究内容。
土工离心模型试验过程中模型与试验系统随离心加速变化而具有相对运动的特征,增加了其变形测试的复杂性[7]。根据量纲相似原理,假设N(通常10≤N≤200)倍重力场下模型中的变形测量误差为ΔL,相应原型中的误差则为NΔL。因此,高精度、小误差是离心模型试验变形测量的必然要求[8]。文献[9]虽然考虑了激光支架的回弹,但认为离心机减速时支架回弹后土体再回弹,基本假定和处理方法并不合理。基于图像分析的面测量方法一般对设备依赖程度高,算法复杂且不开源[10]。土工离心模型试验模型变形机理及发展规律、变形测试手段基本原理仍缺乏系统分析,变形测量及分析技术还需要进一步深入研究。
本文变形测试方法以路堤下刚性桩复合地基离心模型试验的地表沉降及断面变形为测试内容,基于重力场中土工模型的变形特点分析了激光测距法的形变组成,讨论支架变形的影响,并提出了一种基于鱼眼图像处理的实用断面变形分析方法。
1 离心模型试验及变形测试
试验平台为南京水利科学研究院土工离心模型试验室400 g·t土工离心机,相似比尺为60,原型软土地基包括9.6 m厚的软弱土层和其下9.0 m厚的粉质黏土持力层,路堤堆载高度6.0 m,堤顶宽度为39.0 m,现浇混凝土大直径薄壁管(large-diameter cast-in situ concrete pipe pile,PCC)桩原型外径为1.2 m,壁厚0.15 m,桩长12.0 m,穿过软土层后嵌入持力层2倍桩径深度。缩尺后的离心模型如图1所示。利用对称性,离心模型为半幅路堤;通过线性提高离心加速度的方法进行路堤荷载施加。

图1 路堤下刚性桩复合地基离心模型试验Fig.1 Centrifugal modelling of rigid pile composite foundation under embankment
本次离心模型试验的变形测试内容及布置方法包括:
1)使用激光测距仪测量路堤下复合地基的桩顶、桩间土沉降,如图2(b)所示。激光测距传感器通过支架固定在模型箱顶部,自制尼龙柱沉降标的底盘位于桩顶(或桩间土)位置,即图1所示路中断面的桩间土测点S1和桩顶测点P1,路肩断面的桩间土测点S2和桩顶测点P2,通过细长尼龙柱穿过路堤土连接顶部激光反射片。试验过程中通过激光测距仪实时测量传感器与反射片之间的距离变化获得测点竖向变形;本次试验共布置了路中断面位置的桩及桩间土、路肩断面位置的桩及桩间土2组(共4个)测点(图1)。本文分析并标定了加、减速过程中激光测距仪支架变形随加速度的发展关系,并对测试结果进行了修正;
2)横断面网格变形(如图2(c)、(d)所示)。复合地基模型制作完毕后,拿掉模型箱一侧的透明有机玻璃,在横断面上布置横竖正交的网格后装回透明有机玻璃;将模型箱放置于离心机挂篮并使用高清摄像头采集网格面的实时图像,使用后文提出的基于鱼眼图像矫正的断面变形实用分析方法处理不同时刻的网格图像可以获得离心试验过程模型横断面的变形发展规律;

图2 离心模型试验变形测试Fig.2 Deformation testing in centrifugal test
3)试验结束拆除有机玻璃面人工复测网格坐标。
2 变形测试分析方法
2.1 激光测距法分析
如图3所示,试验前离心加速度为0,激光测距仪在O点,与反射片初始距离为H0;Yi(Yd)为加速(减速)阶段支架相对初始位置的变形量;X为离心加速度。经过时间t后,离心加速度达到Ng,测距仪下沉至O′点,激光反射片始终随地表运动,此时测距仪与反射片距离变为h(t)(相当于试验直接测量值),令地表实际沉降量为S(t),支架下沉量为Δ(t),关系为:
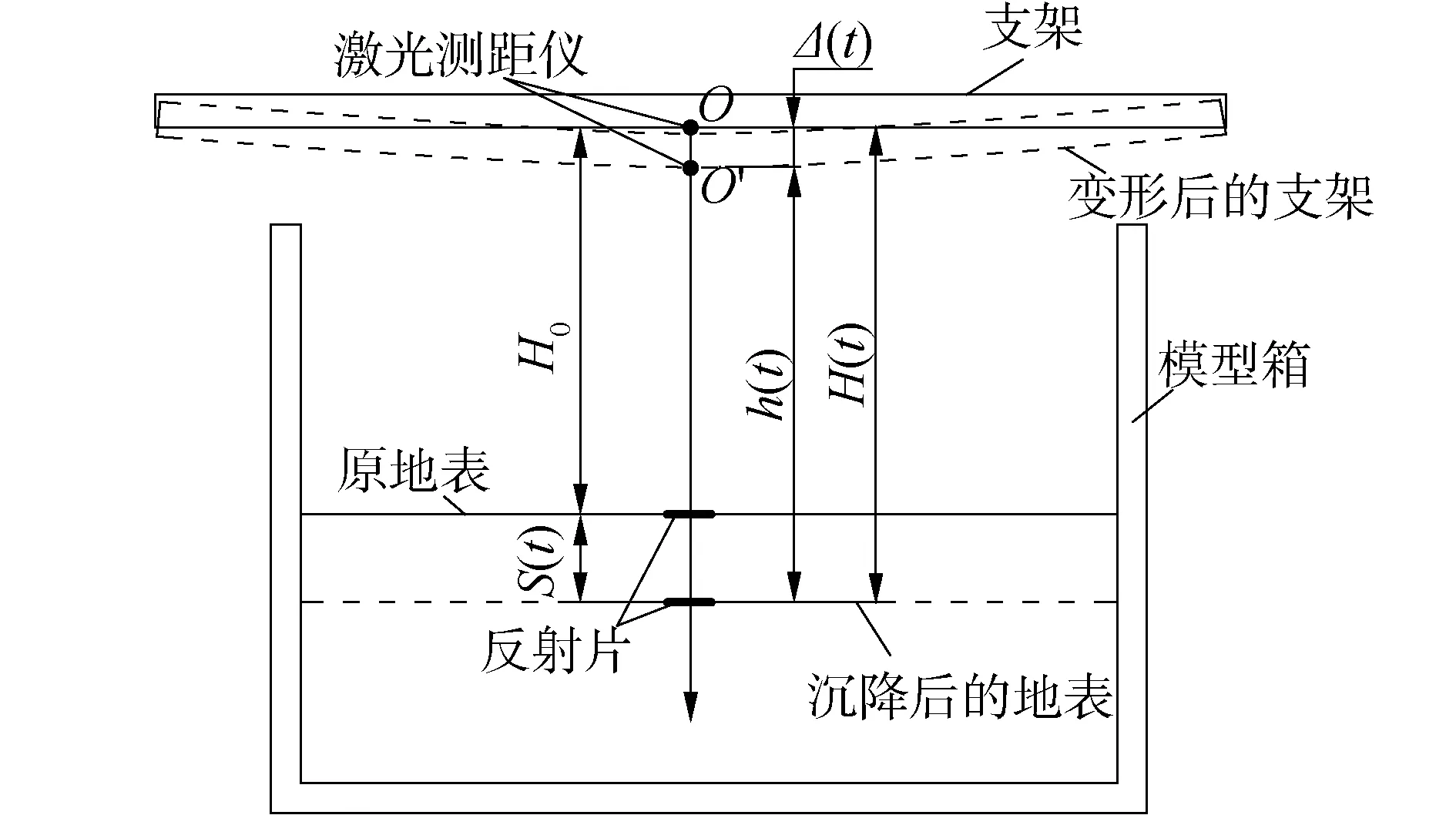
图3 激光测距原理Fig.3 Schematic diagram of laser ranging method
S(t)=H(t)-H0
(1)
H(t)=h(t)+Δ(t)
(2)
式中H(t)为沉降后的地表与变形前激光测距仪的垂直距离。地表实际沉降量S(t)为:
S(t)=(h(t)-H0)+Δ(t)。
(3)
地表实际沉降量包括2部分:1)激光测距仪直接测量距离h(t)与初始距离H0的差值;2)支架下沉量Δ(t)。通常激光测距仪的支架变形量很小,但当离心加速度倍数N较大时,支架的变形误差就不可忽略。本文标定了加、减速过程中激光测距仪支架变形随加速度的发展关系,因而可以通过式(3)考虑加速度变化过程中的支架变形进而计算地基实际沉降量。图4所示为路中测点支架的标定数据,加载阶段可以视作为过原点的直线,即支架下沉量Δ(t)与离心加速度线性正相关;卸载时Δ(t)同样与离心加速度为线性相关,但停机后有残余形变,并需要考虑60g时刻变形连续。
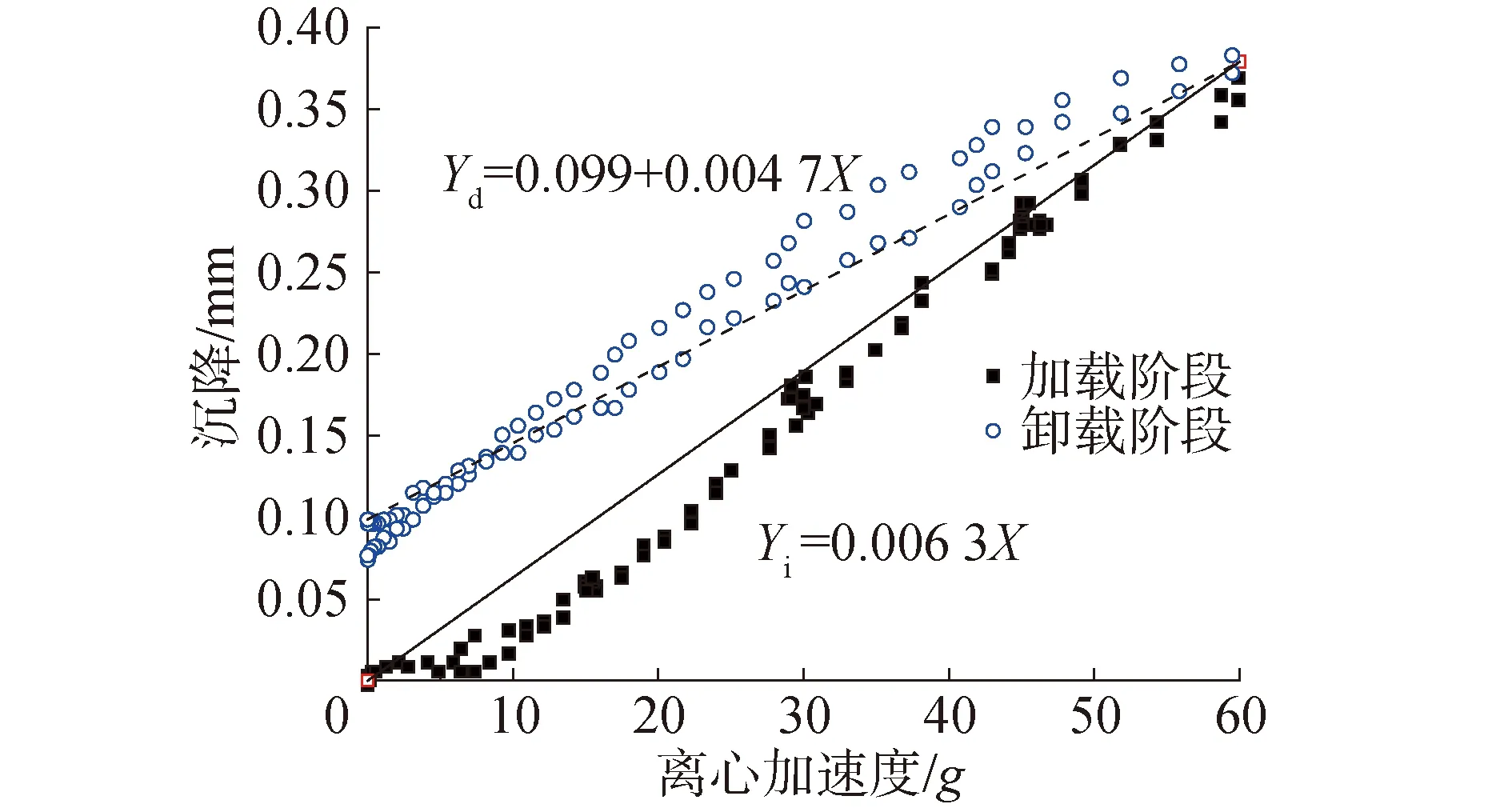
图4 激光测距法支架标定Fig.4 Bracket calibration of laser ranging method
2.2 断面变形分析
使用相机采集试验过程中模型断面网格图像(图2(c)、(d))并处理可以获取不同时段的断面形变量。试验中离心机挂篮摄像使用了鱼眼镜头,该镜头具有体积小、视角广且不易损坏等优点,广泛应用于机器人导航、监视和监测等领域的图像及视频采集[11]。然而,鱼眼图像存在固有失真,拍摄的模型断面网格存在图5(a)所示扭曲,因此须纠正鱼眼图像畸变,将模型网格还原至二维正交坐标系中以分析不同时刻的断面变形。常见的鱼眼镜头矫正模型有球面模型、对数极限模型、多项式变换模型等[12]。本次试验所采集的鱼眼图像畸变程度较小,基于试验过程相机与有机玻璃断面之间视距不变的特点,提出一种采用二元三次非线性多项式函数映射纠正鱼眼图像畸变的方法。试验中模型箱在离心机挂篮的平面位置不改变,即图2(d)所示摄像头与复合地基模型网格断面的水平距离不变。因此,尽管复合地基断面在试验过程中产生形变,但其断面的扭曲程度不发生变化。假定每张鱼眼图像与未畸变的二维网格之间存在图5(b)所示固定的函数映射关系f。本文将这种映射关系具体为鱼眼网格像素坐标与其未畸变二维坐标之间的函数,通过试验前未变形的已知图像数据可求解这种映射关系f。当离心加速度改变时,模型箱、镜头、复合地基3者之间存在两两相对位移,假定模型箱为绝对刚性,只有复合地基相对模型箱的位移才是真正的断面位移。因此,通过映射关系f获取网格的真实坐标(Xt,Yt)之后,必须将其转换为以模型箱为固定参照的坐标才能获得真实的断面变形量。为此,开机前在模型箱有机玻璃面粘贴1个图5(a)所示四边形的白贴,该白贴相对模型箱始终固定不动,将不同时刻断面图像的网格坐标转化为以白贴形心为原点并进行差值计算即可获取复合地基实际变形场。
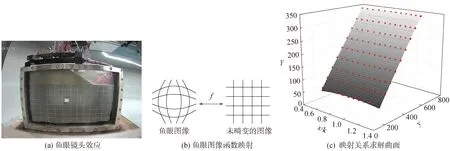
图5 鱼眼图像处理原理Fig.5 Principle of fisheye image processing
基于上述原理,鱼眼图像网格具体处理方法如下:
1)根据初始网格坐标求解鱼眼图像函数映射f。
以离心机启动前已知的初始网格为基准,提取其对应鱼眼图像中网格交叉点的像素坐标(x,y),并求得白贴形心参考点的像素点坐标(m,n);建立像素坐标(x,y)与真实坐标(X,Y)的函数映射关系f。X、Y与(x,y)的映射函数fX、fY形式相同,均为二元三次非线性多项式,只是系数不同。图5(c)为本次试验映射关系求解的曲面拟合图示。参考点真实坐标(M,N),以及初始网格相对模型箱参考点(M,N)的初始网格坐标(X′0,Y′0)分别为:
fX(Y)(x,y)=A+B1x+B2x2+B3x3+C1y+
C2y2+C3y3+D1xy+D2x2y+D3xy2
(4)
(X,Y)=(fX(x,y),fY(x,y))
(5)
(M,N)=(fX(m,n),fY(m,n))
(6)
(X′0,Y′0)=(X-M,Y-N)
(7)
2)求解任意时刻的断面变形量。
对于离心试验中时刻t的图像,同样获取网格像素点坐标(xt,yt)及参考点坐标(mt,nt),根据式(4)~(7)求得其变换后以白贴形心为原点的网格坐标(X′t,Y′t)。自t1时刻至t2时刻的断面变形的增量为:
(ΔX,ΔY)=(X′t2,Y′t2)-(X′t1,Y′t1)。
(8)
3 变形测试验证与分析
根据加速度的不同可将本次离心模型试验分为加速(0~T1)、60g稳定(T1~T2)、减速(T2~T3)和静置(T3~)共4个阶段(图6),对比不同试验阶段模型变形规律可以验证变形测法的有效性并深入分析复合地基离心模型试验系统的变形特点。
3.1 方法验证
图6为路中断面地表桩间土(图1所示S1及S′1点)沉降随加速度的发展曲线,实线为激光测距法所测对应图1所示路中桩间土位置S1的沉降,虚线为本文所述图像分析法在对应图1所示网格测试断面在左起第2、3排桩之间的桩间土S′1测点的沉降数据。上述2个测点均在路中断面,但S1测点位于模型箱前侧透明有机玻璃的内边界,S′1测点远离模型箱边界。二者在不同试验阶段的变形发展曲线规律一致,但模型箱边界效应的存在使离心机加速及稳定阶段模型中部S1激光测点的沉降大于边界网格位置S′1测点。停机静置后,2种测法所得最终残余沉降趋于一致。图7为图像处理所得的60g减速前(T2时刻)透明有机玻璃内壁的总变形矢量图,路面之下的地基以竖向沉降为主,边坡附近区域有较为明显的向坡外的水平位移,但未形成滑动破坏面。断面变形特征符合路堤荷载作用下复合地基形变基本规律。试验结束后拆除模型箱的有机玻璃,将人工测量的网格坐标与拆模前最后采集的1张鱼眼图像处理后的坐标进行对比,平均差值约为1.0 mm,考虑拆模扰动和人工测量读数误差,二者对应良好。
上述现象证明本文所述的图像处理方法能够准确地捕捉路堤下复合地基模型断面的变形特征,测量精度良好。
3.2 边界效应分析
对比激光测距法与图像分析法所测路中断面桩间土沉降(图6),在前2个阶段(0~T2),图像分析法S′1测点沉降值比激光测距法S1法明显偏小(T1~T2阶段路中桩间土沉降差值为3.3 mm,路肩桩间土S2、S′2测点上述差值为3.9 mm);在减速阶段,图像分析法的回弹相对激光测距法有所延迟。尽管试验前模型箱边界做了润滑,但软土的塑流与模型箱边界效应的组合会使试验过程中模型箱有机玻璃面内侧布置的复合地基网格断面沉降小于模型中间位置;本组试验地基强度小(软土层不排水剪切强度11 kPa,下卧层24 kPa),地基形变量较大,边界效应显著。上述沉降变形规律证明了离心模型试验普遍存在的边界效应[1]。同时,由图7可知,受模型箱左侧边界影响,复合地基最大沉降没有发生在路堤对称面位置,而向模型箱中部靠近。
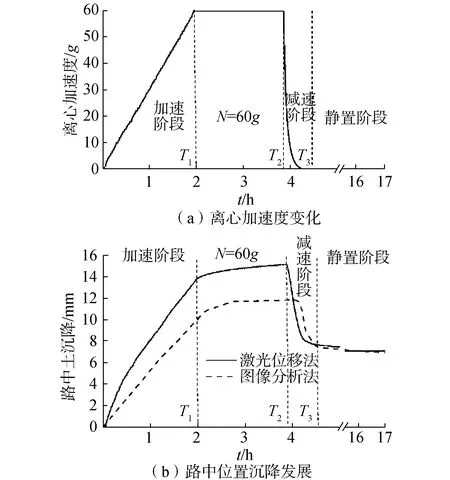
图6 路中断面桩间土位置(S1点)沉降发展规律Fig.6 Settlement development of the subsoil at the central position of the embankment (Point S1)

图7 加速度减小前(T2时刻)的断面变形矢量Fig.7 Deformation vector map of cross-section before acceleration decreases (at time T2)
3.3 加减速过程变形分析
根据土的变形分类[13]并结合本文复合地基离心模型试验工况,模型系统变形包括地基固结排水沉降、伴随加速度改变的加卸载过程瞬时变形、激光支架变形以及试验系统(模型箱、摄像支架等)的微小形变。离心加速过程是离心模型试验的必经环节,本文以线性提高加速度施加路堤荷载,加速度由0~60g共需2 h(图6)。根据相似原理,按照离心加速度平方进行积分后对应现场100 d;图7所示变形矢量图表明在路堤荷载作用下,地基稳定性良好。将加速期间复合地基的沉降分为不可恢复的塑性排水沉降和可恢复的弹性沉降2部分,并认为试验结束停机减速阶段复合地基的回弹都是弹性的,并拟合为加速度的6次多项式函数(卸载回弹数据拟合如图8所示),即停机过程中地基模型的弹性变形量y随加速度x的变化为:
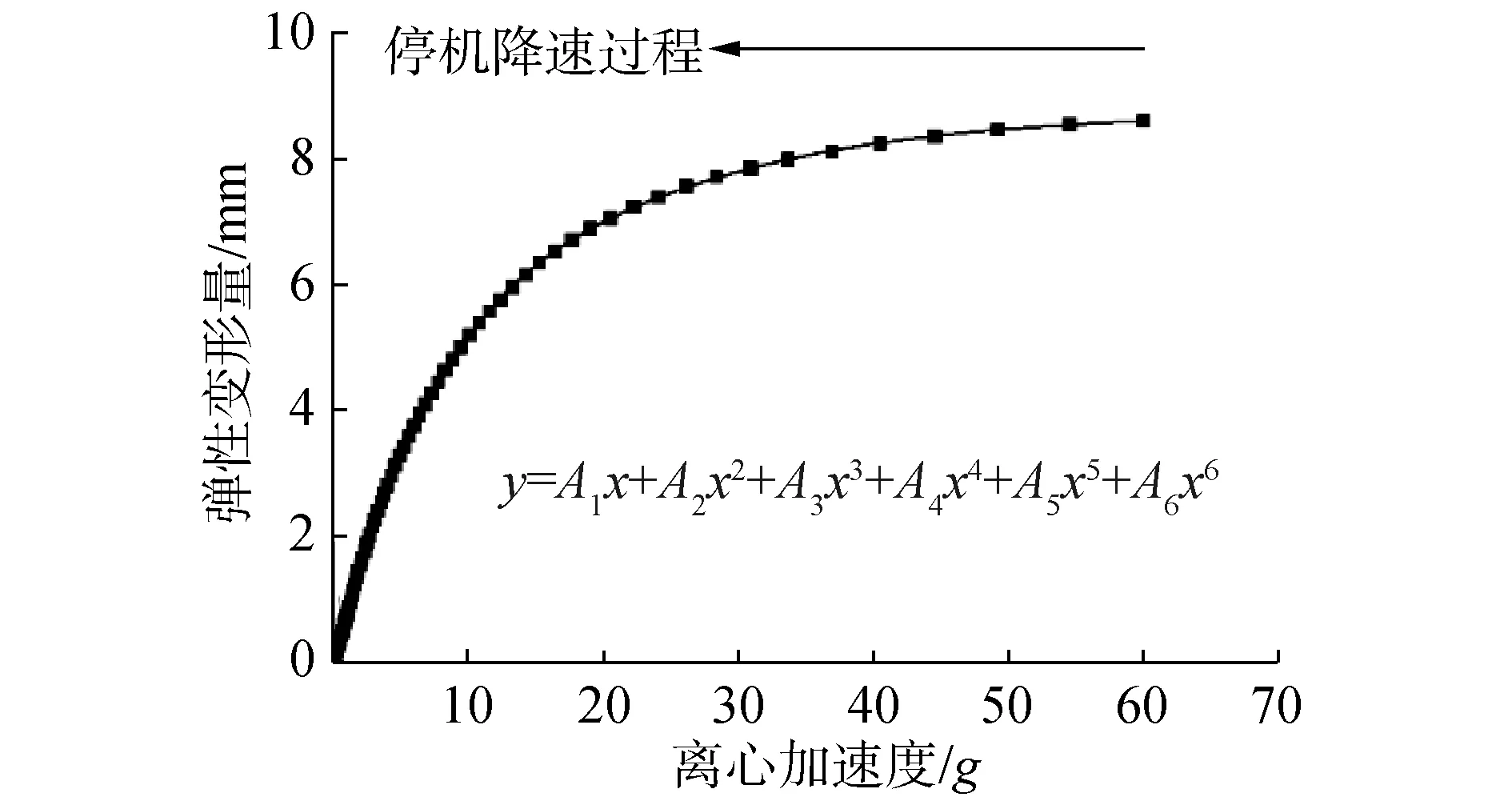
图8 卸载回弹多项式拟合Fig.8 Polynomial fitting of unloading rebound
y=A1x+A2x2+A3x3+A4x4+A5x5+A6x6
(9)
式中A1~A6为待定系数。
假定复合地基模型加速过程中的弹性沉降与减速过程中的弹性变形相对应,即加速过程中复合地基模型的弹性沉降随加速度的变化同样为图8所示,那么总沉降扣除弹性变形即为塑性排水沉降。
3.4 变形组成分析
图9对比了离心机加速及60g稳定阶段2个时刻路中断面S1测点(图6的T1、T2时刻)的变形组成。在60g下离心机共运行115 min(对应原型288 d),按照本文所述分析方法,至减速前时刻复合地基的弹性沉降为6.8 mm,加速阶段及加速度稳定阶段的塑性变形量分别为6.9、1.5 mm,3种形变分别占总变形的45%、45%和10%;加速阶段(相当于路堤填筑阶段)的变形量占总变形量(对应图6的T2时刻)的90%。本组试验地基强度小,路中桩间土S1测点最大总沉降量为15.2 mm,对应原型0.90 m,显然复合地基离心模型初步设计沉降控制效果还需要改进,可通过增加桩长、减小桩间距等措施减小沉降量。

图9 加速度稳定阶段变形组成Fig.9 Deformation composition in stage of acceleration and stabilization
图6所示停机阶段的回弹量为6.8 mm,停转后持续观测12.8 h,此间应力场虽不发生变化,但仍有0.9 mm的回弹(图10),该部分为软黏土的流变。停机时地基由高应力状态变为低应力状态时,土体发生回弹,能够瞬间恢复的变形已在卸载时恢复,至1g重力场时模型达到暂时的平衡,而粘性土颗粒外的薄膜水在不同方向厚薄存在差异,土体内部颗粒各方向的受力并不平衡,薄膜水的迁移伴随着颗粒位置调整;而由于粘滞性大,薄膜水迁移及伴随的颗粒调整缓慢,黏土体积流变缓慢发生[13],宏观表现为模型土发生微量的回弹。激光测距和图像分析2种方法在试验静置阶段的沉降测值趋于一致,说明模型边界位置及中间位置在试验后的残余塑性变形一致,因此断面的残余塑性变形量可以代表模型整体的残余塑性变形。

图10 减速及静置阶段回弹变形Fig.10 Rebound deformation in deceleration and static stage
3.5 测试误差分析与控制
激光位移传感器所测仅是传感器与反射片之间的距离。尽管激光支架刚性大,但加速度增加至60g时,路中断面S1测点上方的支架仍有0.4 mm的沉降,占复合地基总变形的2.9%(图9(a)),不考虑支架修正的直接测量沉降小于实际沉降,误差为激光位置支架的变形量,且随加速度增大而线性增大(如图3、4所示)。
本文提出的断面变形分析方法能够考虑离心模型试验系统各部分之间(地基土、模型箱、相机支架)相对运动特性,并能有效地矫正鱼眼图像畸变,处理方法较为实用。根据所述原理,运用该法进行变形分析时其误差来源主要包括:断面网格布置误差,网格图像坐标采集误差及其引起的映射函数拟合误差等。如图5所示,鱼眼图像坐标与真实网格坐标的映射关系f对初始网格布置的准确性依赖较高,因此,必须严格控制模型断面网格制作精度以获取准确的函数映射;断面网格特征点数量直接影响映射函数拟合求解精度,在模型允许的范围内应布置尽量多的测试标点。相机视轴线应对准监测断面中心位置,并与监测平面的法线平行;固定相机的支架应牢固,避免试验过程中发生松动带来的偶然误差。
4 结论
1)激光支架变形标定表明,忽略支架变形的直接沉降测值小于实际沉降值,本试验60g时支架变形占比为2.9%;建议在离心模型试验中使用激光测距法前进行支架标定。
2)本文提出的基于鱼眼图像处理的断面变形实用分析方法能够准确地捕捉复合地基模型断面的变形特征,且测量精度良好。
3)测试表明离心机减速阶段地基弹性回弹变形为加速度的6次多项式函数,此规律可以分离路中断面桩间土测点加速阶段的弹、塑性沉降。本次复合地基离心模型试验中加速阶段变形量占试验总沉降的90%,其中弹性变形和塑性排水变形各自占半。
文中变形分析所涉及的假定(试验过程中鱼眼图像网格与真实坐标的函数映射不变、忽略减速停机阶段的排水变形等)及相关误差分析仍需与PIV等测试方法做进一步验证。此外,应进一步改进离心模型试验及分析方法考虑并减小边界效应的不良影响。
——以徐州高层小区为例

