水槽边壁效应对四柱结构准陷波现象的影响
纪翀,杜一豪,姜胜超
(1.大连理工大学 船舶工程学院,辽宁 大连 116024;2.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
近些年,海上资源开采逐渐向深海发展,浮式海洋平台逐渐受到了越来越广泛的关注,这些平台通常由多根大直径立柱组成,在某些恶劣海况下,波浪上涌对平台下甲板产生冲击,产生较大的作用力与倾覆力矩。因此,充分考虑波浪作用下立柱作用力及附近自由水面变化是浮式海洋平台设计的关键。目前在波浪干涉现象领域已经有了大量研究,Maniar等[1]对100根直线排列的圆柱的波浪力进行了研究,发现在某一频率作用下,圆柱所受波浪力显著增大,出现类似准陷波的现象。Evans等[2]研究了波浪作用下柱群内部产生的一阶准陷波现象,并发现准陷波现象发生频率与结构的尺寸和布置形式密切相关,且发现时的波面分布具有明显的对称与反对称特征。OHL等[3-4]对规则波和不规则波作用下张力腿平台附近的波浪场变化进行研究。通过数值结果与实验资料的对比,发现通过线性绕射理论获得的数值计算结果和实际情况较为拟合。然而,该工作并没有对复杂的准陷波现象开展深入的研究。文献[5-9]对多柱结构准陷波现象展开了更加深入的研究工作。在水槽中圆柱体绕射研究领域中,Ursell[9]和Masashi[10]分别提出了高效求解圆柱体的二维绕射问题和将水槽中的格林函数分解的方法。Bennet等[11]提出了基于波长远小于水槽宽度的平面波近似方法,可以求解任意形状的轴对称体。宁德志[12]将快速多极子展开的方法用于水波问题的计算,基于非线性时域理论,对数值波浪水槽中圆柱周围波面与波浪载荷计算结果与开敞海域进行对比。赵一帆[13]采用源汇分布法,以满足水槽边壁条件的格林函数建立了数值模型,以水槽中座底且穿透水面的等截面柱体为研究对象,并利用波能流守恒关系验证了计算方法的正确性。
在对多柱结构周围波面分布的研究中,通常会采用模型实验的方法,而模型试验往往在水槽中间进行。为了探究边壁效应对准陷波现象的影响,本文基于理想流体假设的势流理论,借助水动力计算软件HydroStar对三维圆柱状浮体的波浪绕射进行分析,研究势流对波浪与四柱结构相互作用问题,分别对有无边壁水槽时四柱结构周围波面特征进行对比,并着重分析了圆柱半径对准陷波现象的影响规律。
1 势流理论与常数元方法
在理想不可压缩流体且运动无旋假设下,流体运动存在速度势Φ(x,t),其满足拉普拉斯方程为:
2Φ(x,t)=0
(1)
波陡ε为:
ε=kA
(2)
式中:k为波数;A为波幅。
对速度势Φ(x,t)按ε进行摄动展开,取一阶近似。当入射波频率为ω时,将时间因子e-iωt分离,从而变为:
Φ(x,t)=Re[φ(x)e-iωt]
(3)
式中:φ为空间复速度势,仍然满足拉普拉斯方程。对于固定不动的物体,可以将空间复速度势进一步分解为入射势φi与绕射势φd,其中,绕射势φd应满足自由水面、物面、水底、无穷远以及水槽侧壁边界条件。
取能同时满足条件的格林函数G(x,x0),并对其与绕射势应用第二格林定理,采用常数元方法进行离散,可建立积分方程为:
(4)
式中n为物面法向量(以指出流体为正)。
开敞水域的情况,采用John推导的满足自由水面边界条件格林函数的形式为:
(5)

对于考虑水槽边壁时的情况,采用源像法消除水槽侧壁积分[13],引入水槽格林函数为:

(6)
式中:αm=(m2π2-k2W2)1/2=-i(m2π2-k2W2)1/2;εm是诺依曼符号:ε0=1;εm=2,m≥1;W是水槽宽度。
对于规则波入射的情况,波面为:
ζ=Re[η(x,y)e-iωt]
(7)
其中:

(8)
式中:g为重力加速度,绕射势φd可通过下述方程求出:
(9)
2 数值试验设置及网格划分
对四柱结构的波浪绕射问题进行数值模拟。数值模型如图1所示,以静水面上各圆柱中心围成正方形对角线交点为坐标原点建立直角坐标系,圆柱中心轴线分别位于(±1.45,0)和(0,±1.45)处,圆柱半径为r=a,相邻圆柱轴线间的距离为L=2.05 m,对角圆柱轴线间的距离为P=2.9 m,吃水深度T=0.5 m,水深d=3.65 m,规则波沿x轴正方向入射。

图1 波浪作用下的四柱结构Fig.1 Four-cylinder structure in regular wave
为了保障数值计算精度,本文采用较密的网格剖分形式,如图2所示。其中,每根圆柱面环向网格划分64个,垂向和柱底径向均划分16个,四根圆柱表面共计划分2 048×4个单元;在进行波面计算时,自由水面使用10 000个四边形结构化网格。为了验证所选网格的收敛性,分别采用前述的远场方法和近场方法对a=0.30 m的四柱结构在x轴方向上的二阶漂移力进行了计算,比较结果如图3所示。从图中可以看出,近场与远场方法计算结果一致,说明本文网格可以获得收敛结果。

图2 四柱结构的物面与自由水面网格划分Fig.2 Sketch definition of four-cylinder structure and the mesh generation

图3 远场方法和近场方法的二阶漂移力比较Fig.3 Comparison of the second order drift force by far field and near field methods
将本文常数元方法无因次化计算结果与文献[6]的高阶边界元方法对比,取r=a,L=4a布置下的四柱结构进行数值模拟,对圆柱内外2侧测点处波高变化进行研究。从图4中可以看出,本文计算结果与文献[6]的数值结果符合较好,说明本文数值模拟的正确性。进一步对本文布置下各圆柱内外两侧关键点波浪爬行情况可以看出,当入射波频率为ka=1.66 时,圆柱内侧测点A出现明显的波面升高,而外侧测点B处波面显著降低,说明波浪能量向圆柱内侧集中,该现象称为准陷波现象。通过上述对比可以看出,本文方法可以对该现象进行正确的模拟,可以应用于后文的数值分析。

图4 数值模型的验证Fig.4 Verification of numerical models
3 开敞海域中圆柱半径对结构附近波浪分布的影响
为考虑圆柱半径对准陷波现象的影响,分别取a为0.30、0.35和0.40 m 3种情况进行研究。如图1(a)与表1所示,在每根圆柱内外2侧距离柱心1.1a处选取共8个测点记录其位置的波高变化,计算结果如图5所示。从图中可以看出,当入射频率ω为5.3、6.8、7.8 左右时各圆柱内侧测点处的波高均出现明显的峰值。对应地,外侧测点在该频率波高较低,波能由圆柱外侧向内侧集中,发生准陷波现象。上述3个频率分别对应着一阶、二阶和三阶准陷波模态。圆柱半径的变化对圆柱内侧测点的波高产生的影响明显大于外侧测点,随着圆柱半径的增大,圆柱内外2侧波面高度分别增大和减小,意味着更多能量从圆柱外侧向内侧转移,更多的能量被“俘获”在四柱结构中。这是由于圆柱半径的增加会导致圆柱侧壁间距离的减小,导致结构内外水体接触部分降低,增大了“俘获”效果。

表1 四柱结构附近波高测点的坐标值Table 1 Coordinates of measuring points near the structure

图5 开敞海域中各测点处无因次波高随频率变化对比Fig.5 Variation of wave elevations at typical points under regular wave in open sea area
为了更好地观察准陷波现象对整体波面的影响,给出3组工况下各阶准陷波现象发生时结构附近无因次波高分布,如图6所示。
从图6中可以看出,各阶准陷波模态的主要差异在于圆柱间波高的分布情况。一、二、三阶准陷波模态分别对应相邻圆柱间存在1、2、3个波,且最大波浪振幅总是出现在圆柱内侧。结构后方出现明显的低波高区域,进一步说明波能被四柱结构所“俘获”,无法传播到结构后方。相对而言,二阶与三阶准陷波模态后方波高明显小于一阶准陷波模态的情况,这主要是由于高阶模态对应频率较高,波长较小,因而结构物遮挡效应更为明显。进一步对图5与图6中准陷波模态发生时圆柱内侧波面随圆柱半径的变化进行研究,根据文献[1-3]的理论解,准陷波模态对应波数为kL=nπ,(n=0,1,2,…),即准陷波现象发生频率只与圆柱间距有关。但是,根据本文数值结果,半径的增大可以使准陷波模态的频率向高频移动,且对高阶准陷波模态影响较为显著,如表2所示。这主要是由于理论解基于无穷多个圆柱平行放置的假设,并且在推导过程中,将圆柱间距转化为水槽宽度。实际上,圆柱半径对准陷波模态的影响不可忽略,导致准陷波现象发生的关键因素实际为圆柱侧壁间距。为验证这一结论,表2给出了准陷波模态发生时圆柱侧壁间距与波长的变化,可以看出,不同条件下kl可以更好地满足nπ的关系,尤其是对于圆柱半径较大的情况。进一步对比可以发现,三阶准陷波模态所对应的自振频率与kl=nπ的关系相比更远,这主要是由于三阶准陷波模态发生时,圆柱间形成的驻波并未在相邻圆柱中心连线附近,而是偏向于结构的外侧,如图6(c)、(f)、(i)所示。上述对比说明了圆柱半径对准陷波模态有显著影响,不仅导致其自振频率的变化,也会导致波面分布特征的改变。

表2 四柱结构各阶准陷波模态的发生频率Table 2 Frequency of different order near-trapped modes of a four-cylinder structure
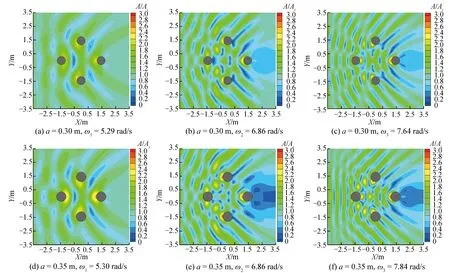
图6 开敞海域中准陷波现象发生时四柱结构周围波面分布Fig.6 Wave distribution around four-cylinder structure when near-trapping phenomenon occurs in open sea area
4 水槽边壁效应对准陷波现象的影响
在上述分析的基础上,对物理模型实验中水槽边壁对准陷波模态的影响进行研究,模型布置如图1(b)所示。以开敞海域下半径a=0.30 m的四柱结构为基础,考虑该结构在W=7 m宽的水槽中心条件下各测点的波面变化情况。从图7中可以看出,在考虑边壁效应的影响后,各测点波面随波浪频率的变化曲线呈现更加剧烈的上下振荡特征,原开敞海域准陷波现象发生频率处的波高显著增加,说明水槽边壁效应对准陷波现象具有显著影响。

图7 水槽侧壁对四柱结构内外侧测点波高变化的影响(r=0.30 m)Fig.7 Influence of sidewall on wave elevations at typical measuring points under regular wave (r=0.3 m)
为对比不同圆柱半径条件下水槽边壁效应的影响,图8给出了3种半径时后方圆柱内外两侧测点波高随频率的变化情况。水槽边壁效应对不同半径圆柱条件下准陷波模态的影响基本相似,各测点波面随波浪频率仍呈现剧烈震荡特征,且峰值个数与发生频率基本一致。为进一步探索上述现象的原因,水槽宽度为波长整数倍时对应频率即为水槽横向自振频率[13],表3通过对比发现横向立波自振频率与图8中的波高变化峰值基本对应。进一步将结构准陷波模态频率与水槽共振频率进行对比,可以看出,水槽共振频率与准陷波频率存在耦合作用,一、二、三阶准陷波频率分别与水槽横向立波自振频率的二、四、五阶模态接近,2种共振模态同时激发,导致对应频率下波高峰值的显著增加,说明水槽物理边壁对准陷波现象具有显著影响。

表3 水槽横向共振频率与准陷波频率的对比Table 3 Frequency of horizontal resonance and near-trapping

图8 不同圆柱半径时水槽侧壁对后方圆柱内外两侧测点波高的影响Fig.8 The influence of the side wall of the flume on the wave elevation at typical measuring points of the rear cylinder
进一步对比发现,尽管圆柱半径对准陷波模态频率有一定影响,但总是对应于水槽横向立波二、四、五阶自振频率,因而水槽边壁效应对圆柱半径的影响并不敏感。
为进一步考虑水槽侧壁对准陷波模态的影响,图9给出了水槽侧壁影响下准陷波现象发生时结构周围的波面分布情况。相比而言,图6中圆柱附近波浪分布多数沿圆柱结构±60°方向呈现条状分布,而图9中圆柱附近波浪呈现出块状分布,尤其是对于二阶与三阶准陷波模态时短波的情况,这主要是由于波浪作用于圆柱后绕射波作用在水槽侧壁后反射的结果。通过与图6对比可以看出,结构附近大波高区域与小波高区域分布总体上更加清晰,说明边壁效应影响下波能向圆柱内侧集中的趋势更加明显。但是,图6与图9中所给出不同准陷波模态时最大波高分布基本相同。通过上述对比可以看出,与开敞海域相比,由于水槽中边壁的反射作用导致水槽横向立波自振模态的产生,更重要的是,波浪在作用于圆柱以后,由于绕射波受到水槽边壁的反射作用,导致波浪波能无法辐射到远场,而是集中于水槽内向下游传播,导致圆柱附近波浪运动显著增大,且波能向圆柱内侧集中的趋势更加明显,这也导致了结构附近最大波高的增加。
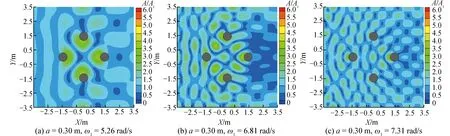
图9 水槽中四柱结构周围的波面分布Fig.9 Wave distribution around four-cylinder structure in channel
5 结论
1)圆柱半径的变化对圆柱内侧测点的波高产生的影响明显大于外侧测点,发生准陷波现象时此差异更为明显。圆柱侧壁间距的改变不仅导致准陷波模态自振频率的变化,也会导致波面分布特征的改变。圆柱侧壁间距离的减小导致结构内外水体接触减少,更多的波能集中到结构内侧。
2)与开敞海域相比,水槽中边壁的反射作用会导致水槽横向立波自振模态的产生。水槽边壁的反射作用,导致波浪波能无法辐射到远场,导致圆柱附近波浪运动显著增大,且波能向圆柱内侧集中的趋势更加明显,这也导致了结构附近最大波浪爬高的增加。
本文的研究工作忽略了圆柱壁附近的流体粘性阻尼和能量耗散对波面的影响,且实际情况下海洋平台并非一直处于静止状态,所以需要借助Navier-Stokes方程数值求解实现更深入的工作,并对水流和波浪共同作用下的多桩柱式结构水动力特性进行拓展研究。虽然本文的研究工作尚有不足,但对开展水槽物理模型试验和优化多桩柱式海洋平台工程设计是具有意义的。

