利用声压场的浅海地声参数贝叶斯反演方法

郑广学，朴胜春1,2,，祝捍皓，张海刚1,2,，李楠松1,2,

(1.哈尔滨工程大学 水声技术重点实验室，哈尔滨 150001；2.海洋信息获取与安全工信部重点实验室(哈尔滨工程大学)，工业和信息化部，哈尔滨 150001；3.哈尔滨工程大学 水声工程学院，哈尔滨 150001；4.浙江海洋大学 海洋科学与技术学院,浙江 舟山 316022；5.浙江大学 浙江省海洋观测-成像试验区重点实验室，浙江 舟山 316021；6.中国科学院声学研究所 声场声信息国家重点实验室，北京 100190)

海洋水体环境参数与地声参数共同构成了水下声传播计算最重要的环境参数，相比水体环境参数，地声参数更难直接测量，因而对其的有效获取研究一直是水声学中的热点课题[1]。由于地声参数的变化会对声压场的分布产生重要影响，因此可以考虑以水听器接收到的复声压作为研究对象来反演地声参数。相比于直接测量的方法，利用声学方法反演可以快速、高效的获取大面积海区的底质参数，避免了人力、物力的浪费，因此受到了广泛的关注[2-5]。近年来，利用声学方法反演地声参数已取得了长足的发展。各种反演方法不断涌现，如：利用传播损失的地声参数反演方法[6]；利用舰船辐射噪声等各类海洋噪声信息的地声参数反演方法[7-10]；利用波导频散特性的反演方法等。但上述地声参数反演方法均着重研究反演问题中正演模型的选择，多仍采用传统寻优算法，如下降单纯形法(downhill simplex，DS)、遗传算法(genetic algorithm，GA)等对目标函数进行求解。但此类算法一般只能给出待反演参数的点估计，无法对参数的不确定性进行进一步描述，且在寻优过程中对算法初始模型依赖很强，容易陷入局部最优解。贝叶斯反演方法有效地估计最大后验概率(maximum a posteriori，MAP)模型参数，进而从统计角度定性和定量分析参数反演结果的不确定性。

基于上述原因，本文以单水听器接收到各距离点上的声压场为研究对象，基于贝叶斯理论，建立了针对浅海考虑弹性海底下的地声参数反演方法，反演对象包括声速、声速衰减和密度3类海底声学参数。

1 反演方法

根据声场信息估计未知海底参数的声学反演方法一般由4部分组成：1)构建声传播模型；2)建立合适的目标函数；3)全局优化算法；4)反演结果的不确定性分析。在本文的反演方法研究中，同样针对上述4部分展开工作。

1.1 浅海声场正演模型

浅海波导中，海底横波声速对低频声信号的传播影响不可忽略[11]，本文研究中选择了如图1所示的浅海参数化模型。其中，z=0表征海面，z轴表深度，向下为正，r正轴表示声场向外传播方向。设水深为H、声源位于水深zs处、密度ρ1、声速c1；海底为半无限弹性介质，各向同性。纵波声速、横波声速、密度、纵波声速衰减和横波声速衰减分别用cp、cs、ρb、αp和αs表示，该5项海底参数也是本文反演时的研究对象。

图1 单层弹性海底的浅海参数化模型Fig.1 Parametric model in shallow sea with elastic bottom

图1模型下，流体层中的各位置声压p(r,z)为：

(1)

(2)

式中：ξ为水平波数；r为水平距离；J0为贝塞尔函数；文献[12]给出了A、B、C、β等参数的具体推导过程及表示式。对式(1)中声压场p(r,z)的数值计算，通常采用简正波方法(normal mode method，NMM)及快速场方法(fast field method，FFM)[13]。考虑此模型为浅海环境，FFM更适合用于声场的快速计算，故本文选择FFM完成对上述参数化模型下声压场p(r,z)的数值计算。

在完成对声压场p(r,z)数值计算的基础上，需建立恰当的目标函数来衡量实测声压p(r,z)与理论预报声压p′(r,z)间的适配程度，并通过对其寻优求解便可实现该模型下各海底参数的获取。

1.2 目标函数与优化算法

贝叶斯方法用于反演问题时，观测数据向量d和模型参数向量m被视为随机的。根据贝叶斯理论有:

P(m|d)=P(d|m)P(m)/P(d)

(3)

其中，P(m|d)为后验概率密度(posterior probability density，PPD)。条件概率密度P(d|m)定义为似然函数L(m)，为某一(固定)测量数据d下m的函数，代表数据提供的信息，用于衡量在模型参数m下模型预报结果和数据的适配程度。P(m)为先验概率密度，表示模型参数先验信息，P(d)为测量数据的概率密度函数[14-15]。因此，后验概率密度既包含数据信息，也包含模型参数的先验信息。且P(d)与m无关，可以看作1个常数，所以式(3)可化为：

P(m|d)∝P(d|m)P(m)

(4)

根据贝叶斯理论，目标函数是在高斯数据误差的假设下基于似然函数建立的，似然函数作为某一指定测量数据下模型参数的函数，代表了数据不确定性分布[14-15]。本文使用的目标函数为：

E(m)=ln[B(m)|p|2]

(5)

式中B(m)表示归一化的Bartlett失配器：

(6)

式中：p表示单个水听器接收到的声压场(实测场)，p′(m)为待反演参数向量m的预报声压(拷贝场)，上标“+”代表共轭转置。

从式(6)可以看出，B(m)取得最优匹配时的条件为p(r,z)=p′(r,z)，同时，E(m)取得极小值。目标函数的建立，将对m的反演问题转化为在寻优范围内对式(5)的极小值求解问题。根据贝叶斯理论，上述待反演参数的PPD将依据Metropolis准则采样[16]给出，并从统计角度对其进行不确定性分析。

2 声场正演模型仿真分析

本文在完成了声场建模、确定了目标函数及寻优算法的基础上，利用数值模拟，对比图1模型下各海底参数与其反演结果，对研究方法进行验证。

2.1 声传播特性分析

图2给出了利用FFM计算所得图1所示浅海环境下，1～1 500 m 100 Hz声信号声压场的仿真结果，以传播损失(transmission loss，TL)曲线的形式给出。

图2 5项参数对TL的影响程度分析Fig.2 The impact of five parameters on transmission loss

仿真中，设声源深度为zs=20 m，接收点zr位于水下10 m处，表1给出了仿真中各海洋环境参数。图2(a)～(e)中的实线对应利用表1中各参数真值的计算结果，5项地声参数取讨论值时的计算结果分别用点线(较小值)和虚线(较大值)表示。图2(f)中应用“距平”的定义[17]，视设定的环境参数真值计算所得传播损失为均值，视各参数的讨论值计算所得传播损失为离散值来计算距平，用5项地声参数讨论值的距平大小来衡量各参数变化对传播损失的影响程度。

表1中各参数的讨论值均设定为真值偏移±10%，在此基础上讨论各参数变化对声压场的影响程度。从图2(a)～(e)的中可以看出，5项参数的变化对TL曲线影响程度各不相同，从图2(f)中5项参数讨论值的距平大小可以看出，在各参数均偏移±10%的情况下，改变某一参数对TL曲线的影响程度从大到小依次为cp、cs、ρb、αp、αs。因此，5项海底参数对p(r,z)的影响程度可初步定性为：cp、cs>ρb>αp、αs。

2.2 目标函数对各参数的敏感度分析

在完成了正演建模、声压场数值计算的基础上，本文通过数值模拟仿真分析本文所给目标函数对5项地声参数的敏感度，并讨论该目标函数在反演中的可靠性。仿真中，海洋环境参数真值与各参数寻优区间仍取表1中数值，取各参数设定真值下模拟计算得到p(r,z)为参考真值。本文采用固定变量法来分析目标函数对单个地声参数的敏感度时，即其他参数固定，只在讨论区间内改变某一参数计算声压场理论预报值p′(r,z)，由式(5)计算p(r,z)与p′(r,z)间的目标函数值E(m) 作为敏感度评价标准。

表1 海洋环境仿真参数Table 1 The simulation parameters of ocean environment

图3(a)～(e)分别给出了目标函数E(m)随表1中各单项参数变化时的数值变化规律。从图3可以看出，在5项地声参数讨论范围内，目标函数E(m)均只在其真值处取得极小值，且无伪峰或第2极小值，避免了局部最优解的陷阱，证明了该目标函数的可行性。但从图3(f)可知目标函数随各参数变化时的波动程度不一致，在5项参数的讨论范围内，目标函数值波动范围从大到小依次为cp、cs、ρb、αp、αs。因此，5项海底参数对p(r,z)的影响程度可定性为：cp>cs>ρb>αp>αs，进一步证明了图2的讨论结果。

图3 单参数敏感度Fig.3 The sensitivity of single parameter

2.3 仿真反演结果分析

在完成目标函数对5项海底声学参数敏感度的研究基础上，本节通过数值仿真，分析本文所研究的反演方法对目标函数寻优结果的可靠性。海洋环境参数如表1所设，当寻优结束时，各参数寻优结果与仿真真值的对比如图4给出。图中水平线段表示了各参数PPD的均值位置及其方差大小，垂直于横坐标直线段标注仿真真值所在位置，各参数反演结果在表2中给出。

图4 5项参数及其概率密度分布Fig.4 Five parameters and their probability density distribution

表2 寻优结果Table 2 The results of optimization

从图4和表2中的结果可以看出，各参数的仿真真值与反演结果吻合程度较高，均处于其寻优结果的均值与方差的和或差范围内。且各参数的概率密度峰值的尖锐程度也反映了目标函数对各参数的敏感程度，如图4所示，目标函数对各参数的敏感程度为：cp、cs>ρb>αp、αs，这也与2.1节、2.2节的讨论结果相吻合。

为验证数值仿真中反演结果的可靠性，图5给出了仿真环境参数下TL曲线与仿真反演结果计算所得TL曲线的对比图。等间距取12处绘制误差棒，并标注反演结果计算所得TL曲线的误差范围。从图中可以看出，仿真中TL曲线均处于反推TL曲线误差范围之内，证明了该反演方法在数值仿真应用中的可靠性。

图5 TL曲线对比Fig.5 The comparison of TL

3 消声水池缩比实验验证

3.1 水池实验

本文结合消声水池缩比实验[18]，利用实验数据对本文所研究反演方法进行讨论。实验中选取质地均匀、高硬度的塑料板模拟“半无限弹性海底”。

表3给出了实验中各设备的布放参数，其中声源深度zs为87 mm，接收深度zr为84 mm，水深z为182 mm，水中声速c1为1 450.212 m/s由测量水中温度(11.15 ℃)后通过经验公式求得。测量过程中，声源固定不动，发射信号为135 kHz的脉冲信号；接收水听器固定在可移动走架上，采集卡采样率fs为20 MHz，单个测量点分别测量10次以减少随机扰动带来的误差；完成一点测量后，走架带动水听器向远离声源方向移动2 mm(误差不超过20 μm)至下1个测量点，实验中测量点共720个。测量中TL曲线如图6(b)所示，图6(a) 给出了测量中所接收到的第1～100道接收信号时域图。

图6 实验中接收到的信号Fig.6 The signals received in experiment

3.2 反演结果验证与分析

表3列出了各地声参数的寻优范围，以及利用本文所研究反演方法对上述实验数据反演所得到的“海底”地声参数值，同时还给出了利用GA对该实验数据寻优的结果作为对比。

表3 寻优结果Table 3 The results of optimization

图7给出了算法终止时，各参数在寻优区间上的分布及其概率密度分布，与图4相仿，图7中垂直于横坐标直线段标注GA寻优结果所在位置，水平线段表示了各参数取值PPD的均值位置及其方差大小。图8定量给出了参数间的相关系数矩阵图。

从表4、图7和图8的结果中可以看到：首先，各待反演参数的GA寻优结果均处于均值与方差的和或差范围内，证明了利用贝叶斯反演方法获得的结果与传统反演方法得到结果相吻合。另外，方差的相对大小从一方面也反映出该参数反演结果不确定性的大小。其次敏感度较小的参数对目标函数贡献也较小，在图8中表现为该参数与其他参数的相关性偏小，如αp和αs；换言之，较敏感参数间则表现出较明显的相关性，如cp、cs、ρb，综上，可以看出5项待反演参数的敏感度大小分别为cp、cs>ρb>αp、αs，这也与第2节结论一致。

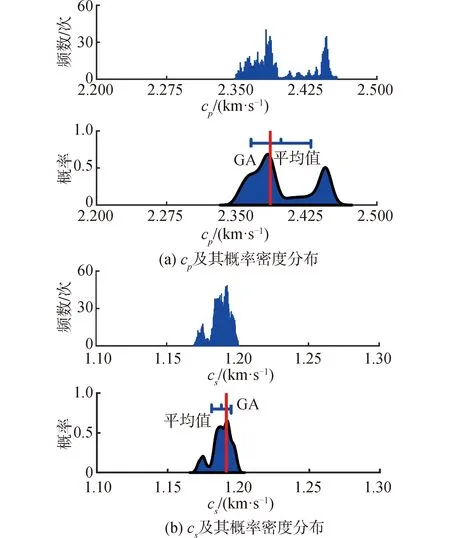
图7 算法终止时5项参数及其概率密度分布Fig.7 The five parameters and their probability density distribution at the termination of the algorithm

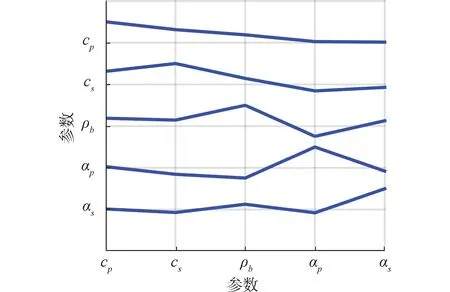
图8 参数间相关矩阵Fig.8 The correlation matrix of parameters

为进一步验证表4反演结果的可信度，图9对比了利用反演结果计算得到的TL曲线和实测TL曲线；图10对比了同一测量点(第470号接收点)，反演所得时域波形与该点实际接收信号的时域波形图(均进行归一化处理)。图9中，实线为实测TL曲线，点线为应用表4反演结果计算所得的TL曲线并等间距取12处绘制误差棒，从图中对比结果可以看到实验中TL曲线基本处于反推TL曲线误差范围之内，证明了该反演方法在实际应用中的可行性；图10中，实线为第470号接收点实测时域波形，点线为应用表4反演结果“预报”的第470号接收点时域波形，从图中对比结果可以看到时域波形计算预报结果与实测信号波形匹配较好，若不考虑信号“拖尾”，相关系数可达0.89，证明了本反演方法在实际应用中的可靠性。

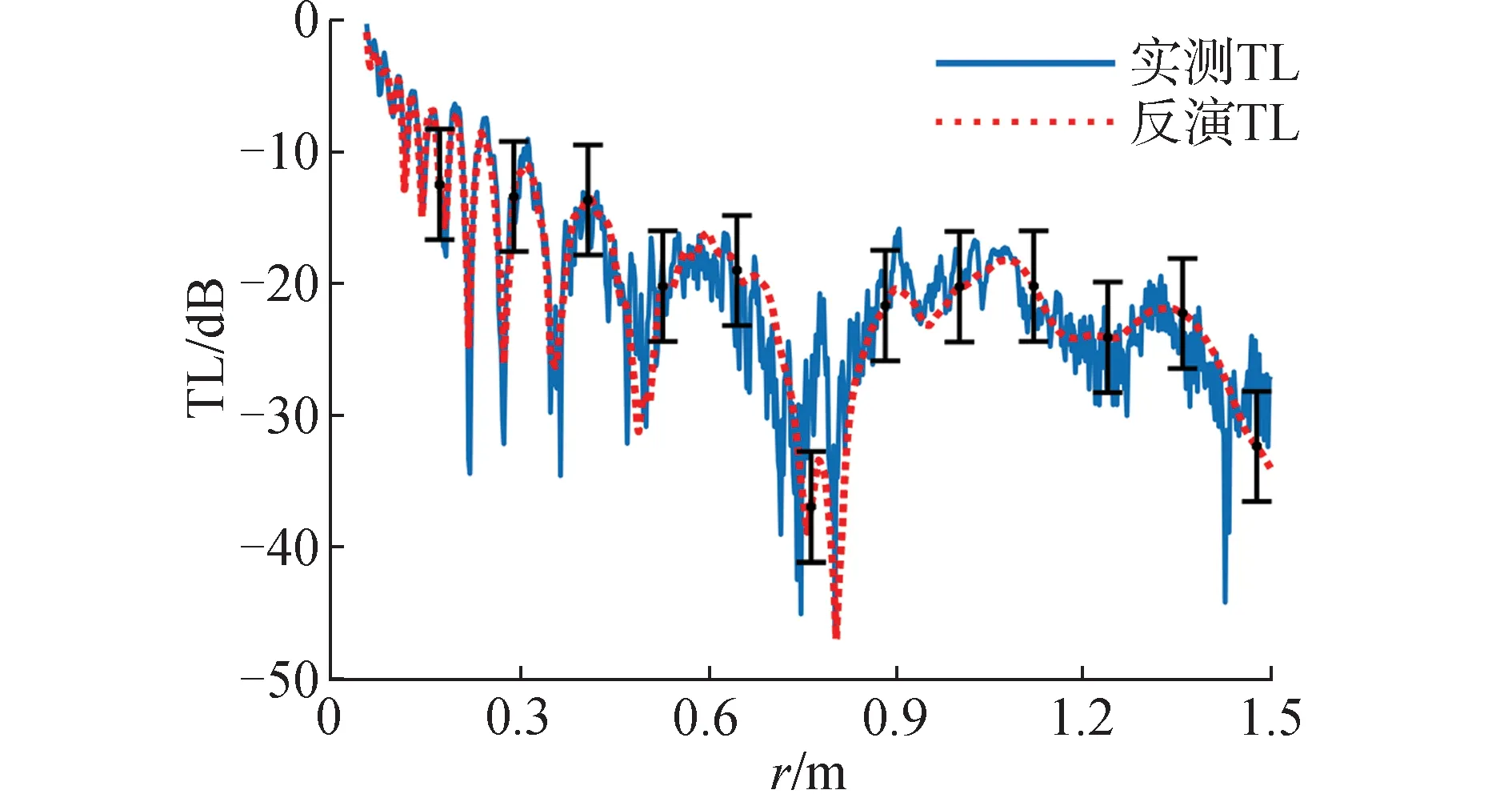
图9 实测TL与反演所得TL对比Fig.9 The comparison of TL between measured and inversed

图10 时域波形对比Fig.10 The comparison of time domain waveform

4 结论

1)贝叶斯反演能够从统计角度给出反映地声参数向量综合信息的后验概率来表征反演结果，同时还能够分析各参数反演结果的不确定性，相比传统只能给出待反演参数点估计的反演方法，反演信息更加全面、科学。

2)根据贝叶斯反演理论，利用本文给出的目标函数，运用Metropolis准则采样，可以较为准确得到待反演参数的PPD。数值模拟和水池实验的结果均表明：PPD分布特性与GA寻优结果吻合程度较好，利用反演参数计算得到的声场特性与测量场基本一致，时域波形相关系数达0.89。

3)从5项地声参数反演结果的不确定性大小来看，在仿真模拟及水池实验的环境下，纵波声速cp、横波声速cs以及密度ρb的不确定性相对较小，对声压场的变化更敏感，5项参数依据敏感程度大小依次为cp>cs>ρb>αp>αs，声场研究结果与反演结果均证实了这一研究结果。