一种适用于MEMS惯组的低维传递对准方法

马 昆，戴居峰，聂晓慧，胡 隽

(1.北京控制工程研究所，北京100094;2.北京轩宇空间科技有限公司，北京100190)

0 引言

使用微机电系统(Micro Electro Mechanical Systems,MEMS)惯组作为敏感器是实现低成本、轻量化捷联惯导系统的主要方案。为解决MEMS陀螺和加速度计常漂大、重复性差、与载体安装误差难以标定的问题,需利用高精度主惯导信息通过传递对准实现对MEMS惯导误差的估计,从而提高导航精度。传递对准方法的评价准则为误差估计的收敛速度及准确度。

影响上述估计效果的主要因素为误差模型的构造、匹配量的选取、滤波算法的设计。误差模型中包含有惯导系统误差和惯性器件误差,其中系统误差主要来源于主子惯导的安装误差、挠性形变、高频震颤、臂杆效应；器件误差则大多考虑陀螺和加速度计的常漂、刻度系数非线性等因素[1]。匹配量的选择会影响传递对准的速度、精度和可观测性,常用的匹配量包括姿态、速度和位置。Kain等[2]首次使用了 “速度+姿态”的组合匹配量将估计收敛速度降为10s,而后国内外学者结合传递对准期间载体的机动特性,对多种组合匹配量的估计效果进行了研究,文献[3]对各种组合匹配量的优缺点及适用场景进行了总结。滤波算法设计方面,Baziw等[4-5]提出了最小二乘法,Schneider[6]则首次使用了Kalman滤波公式。目前,传递对准方法主要使用Kalman滤波算法对组合匹配量进行估计。

本文选取 “速度+姿态阵”进行Kalman滤波估计。为提高收敛速度,相较于传统传递对准方法,本文对误差模型进行了适当简化,只选择作为误差主要来源的陀螺、加速度计常漂及安装误差角进行估计,从而实现了误差估计的快速、准确收敛。本文简要介绍了MEMS惯组捷联惯导系统的组成,对传递对准方法进行了详细推导,开展了数学仿真与跑车试验验证,并对仿真估计误差来源进行了分析,同时对跑车试验中方法的估计效果进行了评价。

1 系统组成

如图1所示,惯导系统的硬件包括MEMS惯组、信号接口电路及导航计算机。其中,MEMS惯组采集载体角速度及加速度,信号接口电路完成惯组数据的接收,导航计算机根据载体角速度及加速度完成导航计算并进行传递对准计算。

图1 惯导系统硬件组成Fig.1 Hardware composition of inertial navigation system

导航计算机、MEMS惯组、信号接口电路、电源转换电路安装在三块电路板上,电路板间通过挠性板连接,三块电路板嵌入安装在圆柱形筒体内,其外部结构如图2所示。

图2 惯导系统外结构Fig.2 External structure of inertial navigation system

导航计算机处理器选用TI公司的DSP产品TMS320C6727,其最高主频为350MHz,内置256KB RAM,BGA256封装(17.2mm×17.2mm),3.3V/1.2V供电,具备完成导航及传递对准计算的能力。接口电路使用FPGA实现SPI串行外设接口,完成惯性测量单元与导航计算机的数据交互。MEMS惯性测量单元使用AD公司生产的ADIS16488,该款产品包含一个三轴陀螺、一个三轴加速度计、一个三轴磁强计和一个压力传感器,使用SPI串行外设接口与外部进行通讯,该惯组的指标如表1所示。

表1 MEMS惯组指标Table 1 Indexes of MEMS inertial units

2 传递对准方法设计

传递对准方法包括误差模型构建、匹配量选取以及滤波算法设计三个方面。在误差模型构建方面,由于MEMS组件零偏重复性较差,无法直接使用地面标定结果,故陀螺常漂Δω、加速度计常漂Δf可以看作导航误差的主要来源[7]。而载体相对主惯导安装误差δμ以及MEMS惯组相对载体的安装误差δA因无法进行准确测量并补偿,成为产生导航误差的另一来源[8]。

确定误差模型后,需要匹配量完成误差模型的表达与观测。在捷联惯导计算中,常用的匹配量有 “速度”匹配、“角速度”匹配、“姿态角”匹配、“姿态阵”匹配,各匹配方案特性如表2所示[9]。本文使用MEMS惯组进行传递对准计算的主要应用场景为平动状态,结合表2的匹配方案特性分析,为实现平动状态下误差的快速估计[10],选取速度及姿态阵作为匹配量。

表2 匹配量特征Table 2 Features of matching data

本文使用Kalman滤波算法对误差进行估计,为提高估计速度,需在构建准确误差模型的前提下降低误差估计向量维度、减少滤波算法计算量。相对传统传递对准方法,本文在误差模型构建时略去了陀螺、加速度计的刻度系数误差及挠曲变形角误差,最大限度地降低了误差估计向量维度。在使用简化模型进行估计时,刻度系数误差将计入安装误差,不会影响估计精度。而挠曲变形角误差在实际物理环境下为一变化量,由挠曲变形及高频颤振产生,但是本文的主子惯导为刚性安装,不存在上述问题。因此,在建模时忽略挠曲变形角,对估计精度影响有限。低维度、适当精度估计误差模型的建立,确保了Kalman滤波算法的快速、准确收敛,误差建模及滤波算法迭代计算过程如下。

构建X轴、Y轴、Z轴分别为地理北、天、东三个方向的导航直角坐标系n,构建主惯导测量坐标系bm、子惯导测量坐标系bs。根据上述匹配量选取分析,匹配向量Zc为

依据捷联惯导导航算法,主子惯导的速度、角速度更新公式如下

主子惯导进行导航计算产生的不一致性主要原因有子惯导测量加速度计常漂、陀螺常漂、子惯导本体系相对载体系安装误差δA以及载体相对主惯导安装误差δμ, 构造测量误差模型有

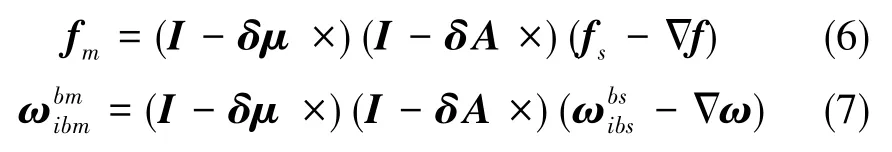
可得匹配量误差模型为(略去二阶小量)

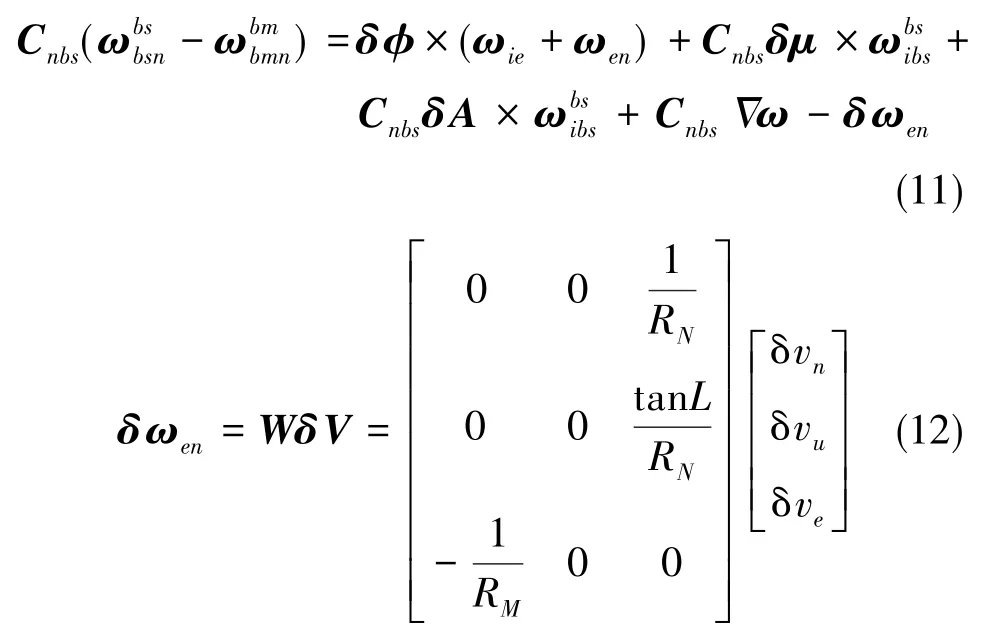
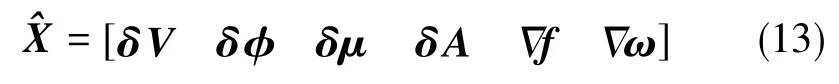
依据误差模型,可得估计矩阵A为

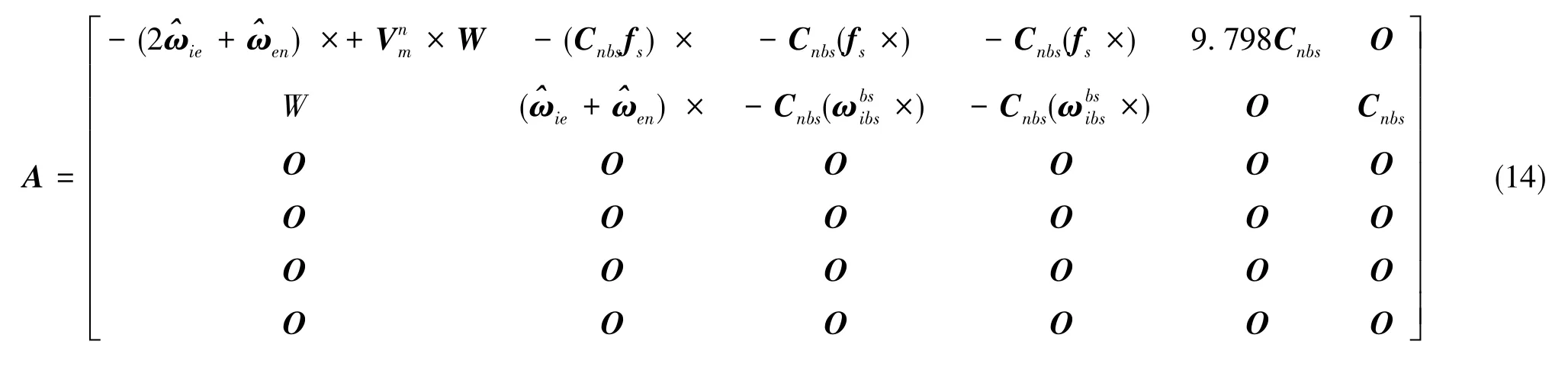
根据观测模型,得到观测矩阵H为

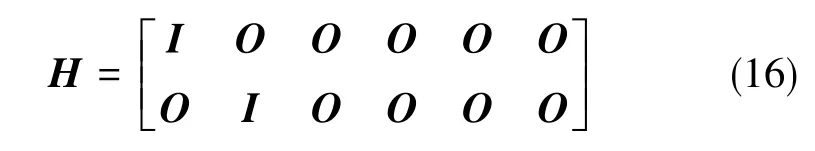
根据Kalman滤波算法,按图3所示的方式进行递推计算。

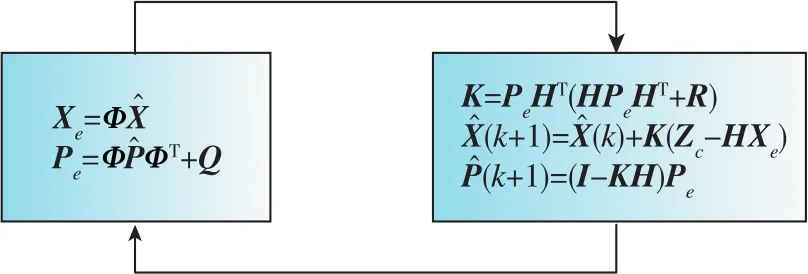
图3 Kalman滤波算法计算过程Fig.3 Calculation process of Kalman filter algorithm

3 仿真及试验验证

3.1 仿真条件及仿真结果

仿真生成的运动轨迹为平动的载体三轴角速度与加速度,以此作为主惯导信息。以主惯导信息为基础,附加安装误差δA和δμ、 陀螺常漂加速度计常漂生成子惯导的陀螺角速度、加速度。主子惯导使用相同的导航算法进行导航解算,并按照第2章所述传递对准方法对子惯导的安装误差、陀螺常漂、加速度计常漂进行估计。

仿真初始滚动角、俯仰角、偏航角分别为0°、0°、45°,初始北、天、东地理速度分别为45m/s、0m/s、 0m/s, 陀螺常漂为 0.574(°)/s、 -0.574(°)/s、0.2(°)/s,加速度计常漂为 0.4g、0.3g、-0.2g,载体安装误差δμ为-0.5°、 1.5°、 1.0°, 子惯导安装误差δA为-0.5°、 0.5°、 0.5°, 主惯导到子惯导的总安装误差为-1.0°、 2.0°、1.5°。 传递对准方法的误差估计曲线如图4、图5所示。图中的ux、uy、uz为载体安装误差向量δμ的元素,Ax、Ay、Az为子惯导安装误差向量δA的元素,为加速度计常漂向量的元素,为陀螺常漂向量的元素。

图4 载体和子惯导安装误差的仿真估计收敛曲线Fig.4 Convergence curves of simulation estimation for installation error of carrier and sub-INS

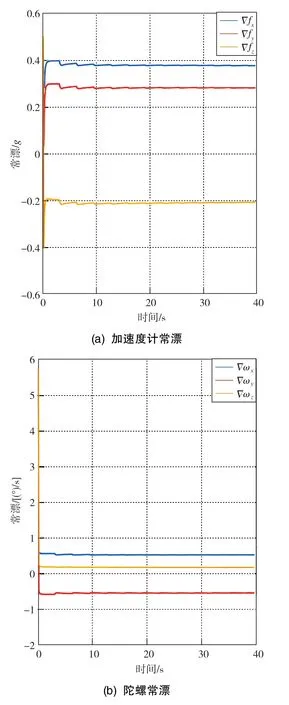
图5 加速度计常漂和陀螺常漂的仿真估计收敛曲线Fig.5 Convergence curves of simulation estimation for constant drift of accelerometer and gyroscope

从误差估计曲线可以看出,误差估计均在10s内实现收敛,估计得出的陀螺三轴常漂为0.53862(°)/s、-0.53289(°)/s、 0.18336(°)/s, 加速度计三轴常漂为0.3786g、0.2829g、-0.2089g,载体三 轴 安装 误差 为 -0.52716°、 0.95691°、0.75063°,子惯导三轴安装误差为-0.52716°、0.95691°、0.75063°,主惯导到子惯导的总安装误差为-1.0543°、 1.9138°、 1.5012°。 上述误差估计结果与仿真设置误差值基本一致,说明该传递对准方法能够实现快速、准确的估计。

载体安装误差δμ与子惯导安装误差δA两者估计结果相同,估计结果与仿真设置值不一致,但是两者相加的总误差与仿真设置值一致。这是由于误差模型中两者估计矩阵一致,因此估计结果也一致。该误差模型不能实现δμ与δA的分别估计,只能完成δμ+δA总误差的估计。

陀螺常漂、加速度计常漂、总安装误差估计结果虽与仿真设置值基本一致,但仍有差别,这主要是由于误差模型中对子惯导相对于主惯导的误差姿态阵理想化为(I-δφ×)Cnbs=Cnbm。而在实际应用或仿真中,CnbmCbsn并非对角阵(为I的理想矩阵),且上述偏差随时间会持续累积增大。

3.2 跑车试验验证

为验证传递对准方法在实际应用中的效果,本文开展了跑车试验。试验中,高精度主惯导及子惯导载体均安装在汽车上。在汽车匀速行驶阶段进行40s的传递对准计算,估计子惯导MEMS惯组的加速度计常漂陀螺常漂、安装误差δA和δμ。传递对准完成后,将估计出的误差对MEMS惯组测量值进行补偿,并开始自主导航。汽车上安装高动态GPS接收机作为基准,对导航结果进行评估,同时与MEMS惯组未进行误差补偿的导航结果进行比较。

设置初始安装误差δA和δμ均为5°、加速度计常漂为0.1g、陀螺常漂为8(°)/s,经传递对准计算40s的误差估计收敛曲线如图6、图7所示。

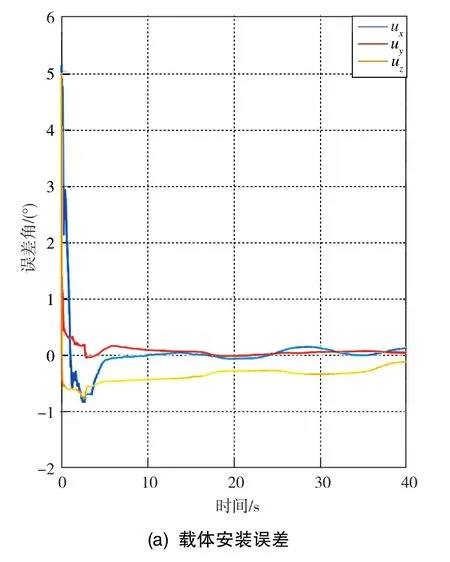
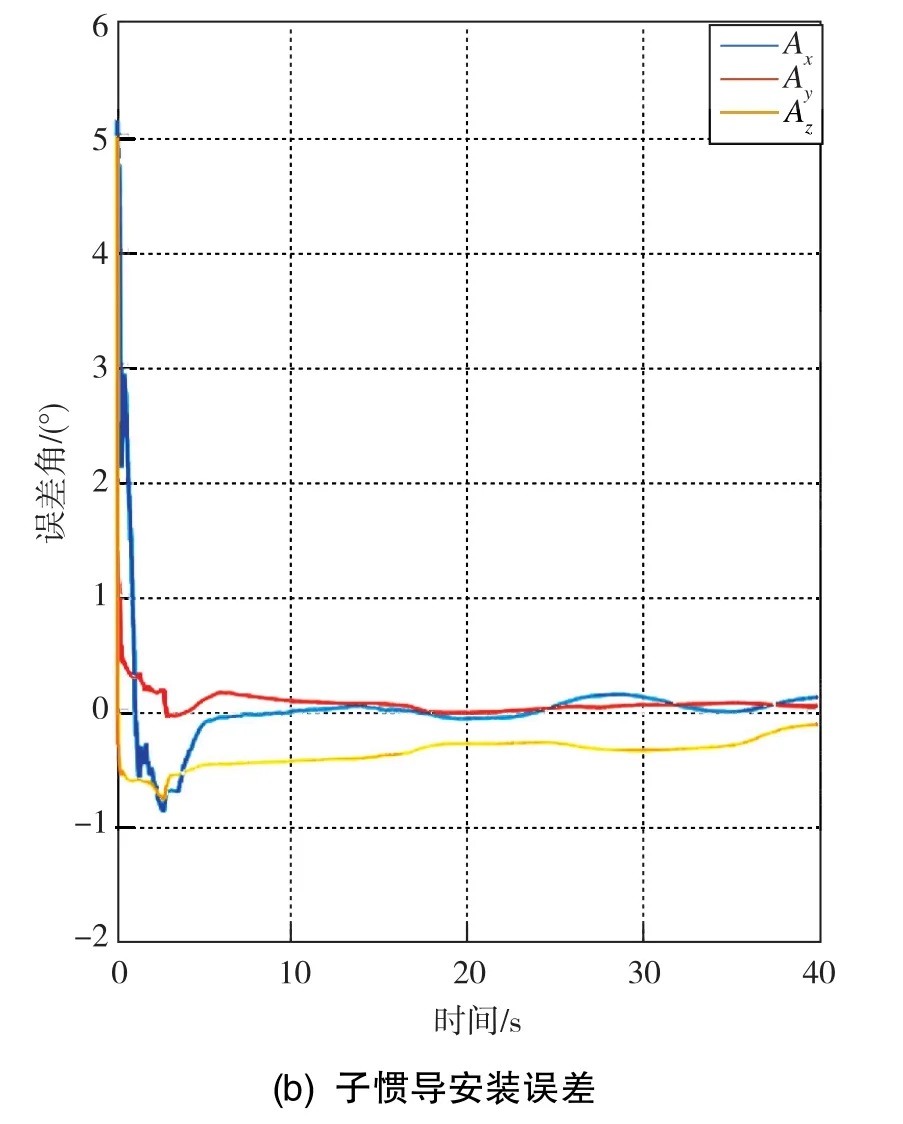
图6 载体和子惯导安装误差的估计收敛曲线Fig.6 Estimation convergence curves for installation error of carrier and sub-INS

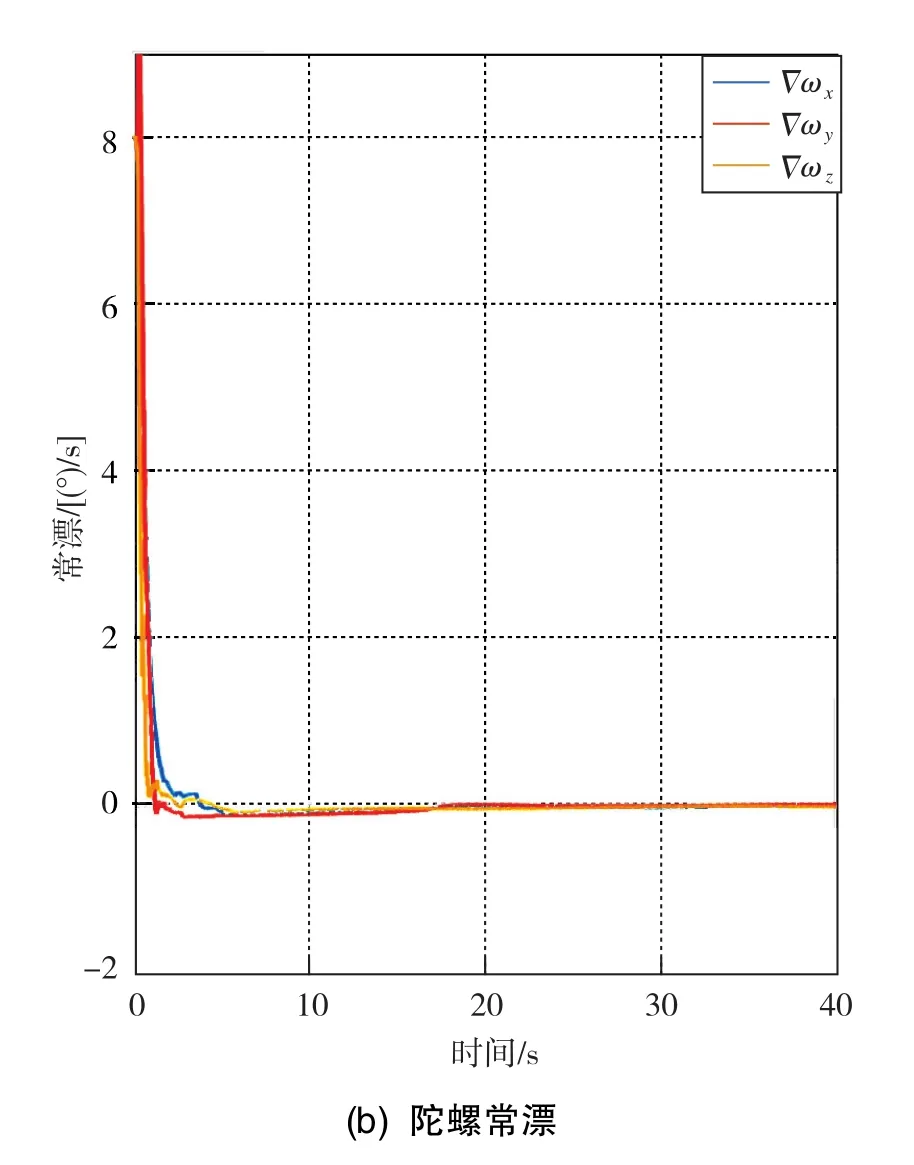
图7 加速度计常漂和陀螺常漂的估计收敛曲线Fig.7 Estimation convergence curves for constant drift of accelerometer and gyroscope

经传递对准方法估计出的载体安装误差δμ与子惯导安装误差δA相同,均为 0.22°、0.05°、-0.18°；加速度计三轴常漂分别为-0.0240g、0.0005g、-0.0310g,陀螺三轴常漂分别为0.0032(°)/s、0.0071(°)/s、 -0.0084(°)/s。

传递对准完成后,使用上述估计结果对子惯导初始姿态、加速度计常漂、陀螺常漂进行补偿并开始导航计算,将补偿后的导航结果与未进行补偿的导航结果进行比较,补偿前后导航20s内导航系(北、天、东)三个方向的导航误差如图8所示。

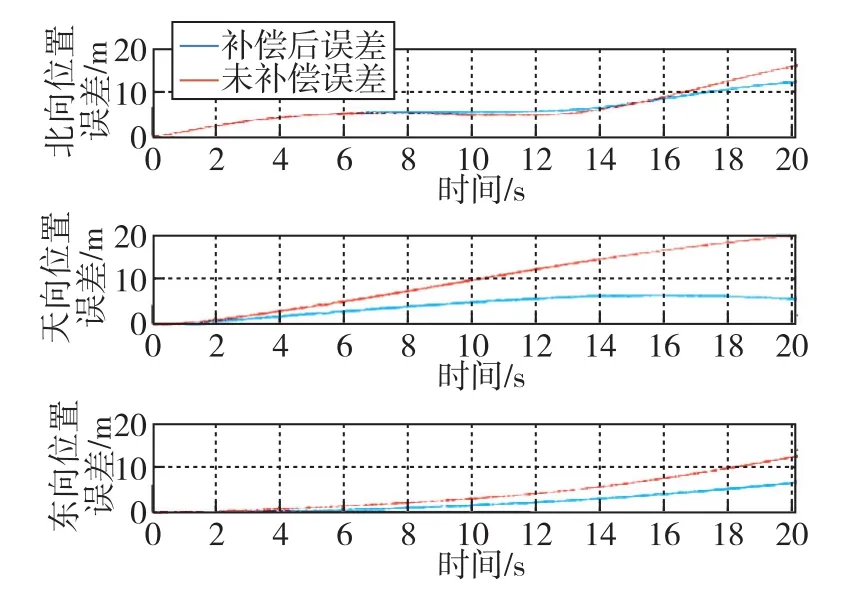
图8 补偿前后导航误差曲线对比结果Fig.8 Comparison of navigation error curves before and after compensation

由图8可以看出,北、天、东三个方向的导航20s后的误差由补偿前的 16.05m、98.94m、62.45m降为补偿后的12.34m、28.35m、33.29m。可见经补偿后,导航精度得到较大提升。

4 结论

本文设计了一种同时使用速度以及姿态阵作为匹配量的Kalman滤波传递对准方法,实现了高精度主惯导对MEMS惯组加速度计常漂、陀螺常漂、安装误差的正确估计。通过数学仿真及跑车试验验证,该传递对准方法估计误差快速、准确,可以较大幅度提升MEMS惯组的导航精度。